重心反向粒子群优化算法在无线传感器定位优化中的应用*

吉滦峦，谢 宏

(上海海事大学 信息工程学院，上海 201306)

0 引 言

节点定位技术是无线传感器网络(wireless sensor networks,WSNs)的主要技术之一，并具有广泛的应用领域[1]。针对无线传感器节点定位问题，国内外学者进行了大量的研究，目前的定位算法主要分为两种：基于测距的算法和无需测距的算法。无需测距的定位算法不需要额外的硬件支持，主要包括质心算法[2]、距离矢量—跳数( distance vector-hop,DV-Hop) 算法[3]、无定形( amorphous)算法[4]和APIT算法[5]。其中，DV-Hop算法实现简单，无需额外硬件支持，具有部署网络成本低的优点，是目前研究最广泛的算法之一。针对DV-Hop算法定位精度不高的问题，许多学者将遗传算法、鸟算法、蚁群算法、粒子群优化(particle swarm optimization,PSO)算法[6～8]等智能算法应用于节点定位，利用群体的智能寻优能力来对未知节点定位，这已经成为一个新的研究方向。

本文为了进一步提高定位效果，在充分研究传统DV-Hop算法和标准PSO算法的基础之上，提出重心反向粒子群优化(centroid oppositional particle swarm optimization,COPSO)算法，用COPSO算法来校正DV-Hop算法定位结果。

1 相关问题描述

1.1 DV-Hop定位

DV-Hop算法主要分为三个阶段。第一和第二阶段通过跳数和平均跳距计算未知节点到锚节点的估计距离di。在第三阶段利用最小二乘法、智能优化算法等方法计算未知节点坐标。

1.2 构建适应度函数

适应度函数用来评价粒子的品质，引导粒子在解空间中的搜索方向。计算适应度函数公式为

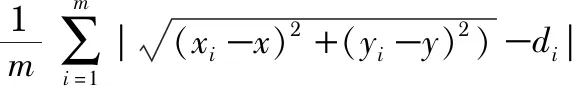
(1)

式中m为锚节点数目，(x,y)为未知节点坐标，(xi,yi)为第i个锚节点坐标,di为节点之间的距离。式中如果fitness(x,y) 最小，则未知节点的解和实际值之间的误差就越小，而此时(x,y)就为最优解。

1.3 标准PSO算法的描述

在PSO算法中，粒子容易过早收敛，陷入局部最优，最终导致算法的搜索精度不高。为了优化PSO算法，将重心反向学习应用到PSO算法，提出重心反向粒子群算法，同时计算粒子的正向解和反向解，扩大粒子搜索范围，提高种群的多样性，并且针对粒子群在后期搜索过程中，粒子收敛精度较低，速度较慢的问题，对算法的粒子运行速度进行改进，进一步提高算法精度和稳定性。

2 COPSO算法的构建

2.1 重心反向学习策略

反向学习(opposition-based learning，OBL)可以提高优化算法的寻优能力。其主要思想是：同时计算可行解及其反向解，择优使用。在此基础上，Rahnamayan S等人[9]提出重心反向学习(centroid opposition-based learning，COBL)策略，本文将COBL应用到粒子群算法，利用整个种群的搜索信息，以整个群体的重心为参考计算反向点，重心与重心反向点的定义如下：

定义1重心。令(x1，x2，…，xN)为D维搜索空间中带有质量的N个点，然后整体重心可以定义如下

M=(x1+x2+…+xN)/N

(2)

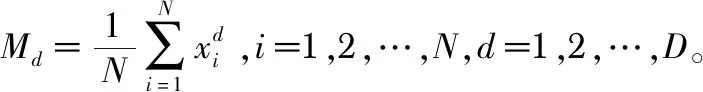
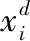
(3)

当反向点超出搜索空间时，按式(4)重新计算反向点

(4)

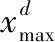
本文首次提出用COPSO对无线传感器定位进行优化，在COPSO算法中种群在前期利用粒子搜索经验充分探索搜索空间，算法后期能更多地保留群体信息，保持种群的多样性。COPSO算法由重心反向粒子群初始化、粒子运行速度和重心反向粒子群更新组成。

2.2 重心反向粒子群初始化和更新

反向粒子群的初始化和更新可以进一步增加种群多样性、提高解的质量[10]。对于一个D维优化问题，设寻优空间有N个粒子，每个粒子按如下方式计算正向解和反向解：

1)随机产生N个粒子的粒子群X，可依据式(5)求得粒子i在D维的正向位置X

(5)

2)根据式子(3)和式(4)计算反向粒子的位置OX；

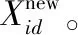
2.3 反向粒子运行速度改进

针对粒子后期容易陷入局部最优问题，本文对粒子速度进行改进，公式为

(6)

式中w为惯性权重;c1,c2为学习因子，r1,r2和r3为在区间[0,1]上均匀分布的随机数;k为[0,1]之间的常数(依实验情况而定);t为当前粒子迭代次数;T为最大迭代次数。算法在粒子速度更新公式中加入了随机波动的线性递增项，在迭代前期粒子速度较大，有利于全局搜索，线性递增项对速度的影响可以忽略；随着迭代次数t的增加，粒子寻优速度减慢，线性递增项值增大，且随机数r3增强了线性递增项的随机波动性，可以有效地使粒子跳出局部最优。

3 定位算法流程

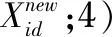
4 仿真试验与结果分析

4.1 仿真环境

在MATLAB2016a的平台上进行仿真实验，拟定无线传感器网络的网络空间为100 m×100 m的二维网络空间，为了使COPSO算法更具有说服力，采用DV-Hop算法进行对比实验，从不同锚节点比例、不同网络节点、不同通信半径三个方面进行仿真。设置参数值k=0.5,种群数N=50,最大迭代次数T=100,惯性权重wmax=0.9，wmin=0.2,学习因子c1=c2=1.494 5。为减小实验中随机误差的干扰，最终结果取20次实验的平均值。采用平均定位误差来评价算法性能，平均定位误差为

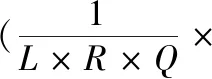
(7)

式中L为未知节点个数，R为通信半径，Q为实验次数；(xi,yi) 为未知节点i的实际坐标，(x′iq,y′iq)为未知节点i在第q次实验的坐标估计值。

4.2 不同锚节点比例时的节点定位

规定无线传感器网络空间的分布形式：传感器节点总数为100个，通信半径为35 m，当锚节点比例分别为10 %,15 %,20 %,25 %,30 %,35 %,40 %和45 %时，两种定位算法定位误差如图1(a)所示。可以看出，随着锚节点比例的增加，这两种定位算法的定位误差整体呈下降趋势，COPSO算法的未知节点定位能力强于DV-Hop算法，定位精度比DV-Hop算法提高了17.24 %，有明显的优越性。

4.3 不同节点总数时的节点定位

规定无线传感器网络空间分布形式：通信半径为35 m，锚节点比例为30 %，对于节点总数分别为50,60,80,100,120,140,160,180，200个时，分别采取两种定位算法定位，定位误差如图1(b)所示。可知，随着网络空间内节点总数的增多，两种节点定位方法的定位精度均得到了有效的提高，误差呈下降趋势。显然，COPSO算法定位误差较小，相较DV-Hop算法，精度提高了13.08 %。

4.4 不同通信半径时的节点定位

规定无线传感器网络空间分布形式：传感器节点总数为100个，锚节点比例为30 %，对于传感器的信号覆盖半径为15，20，25，30，35，40，45,50 m时，分别采取两种定位算法对网络空间内的未知节点定位，定位误差如图1(c)所示。

图1 仿真结果

根据图1(c)可知，随着锚节点通信半径的增大，这两种节点定位算法的定位误差均不断减小，相比于标准DV-Hop算法，COPSO算法精度提高了20.93 %，节点定位精度明显提高。

5 结 论

将算法应用于无线传感器网络节点定位。仿真结果表明:该算法避免了粒子陷入早熟，加快了算法收敛速度，有较好的全局寻优能力，提高了定位性能，与传统DV-Hop算法相比，基于重心反向学习的粒子群算法的网络节点定位效果更好，精度更高。在下一步研究中，将继续优化算法，减小算法的复杂度，进一步提高定位精度。