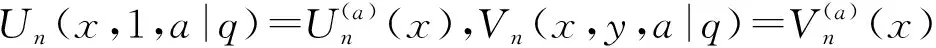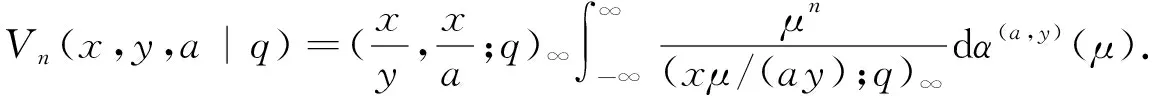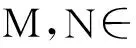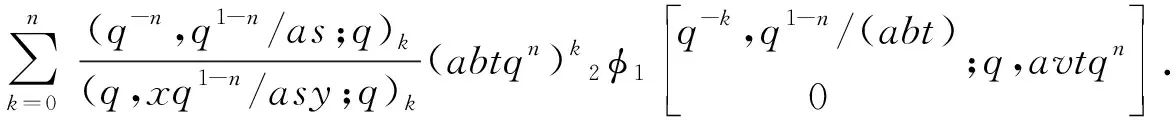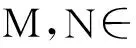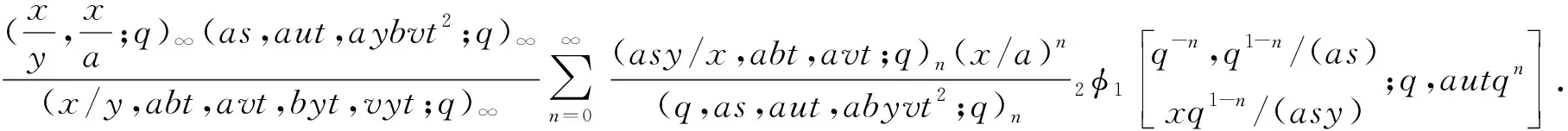矩量积分的推广及其若干应用
徐彬彬,曹 健
(杭州师范大学理学院,浙江 杭州 311121)
0 引言
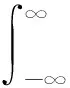
本文遵循文[1]中的符号和术语,并假设0 且(a1,a2,…,am;q)n=(a1;q)n(a2;q)n…(am;q)n,其中m是一个正整数,n是一个非负整数或∞. q-二项式系数和q-二项式定理[1]被定义为 超几何级数rφs[1]被定义为 当分母不为零时,无论是当r≤s时|q|<1且|z|<∞,还是当r=s+1时|q|<1且|z|<1,它都收敛. Al-Salam等[2]根据Rogers-Szegö多项式定义了以下两个离散分布的矩量dα(a)(x)和 dβ(a)(x): 其中α(a)(x)是一个阶跃函数,当k∈N时其跳跃发生在qk和aqk处;而当k∈N时,β(a)(x)函数跳跃发生在q-k.这些跳跃如下: 广义离散概率测度α(a,b)和β(a,b)[3]是 广义的Rogers-Szegö多项式可以用以下的矩量积分[3]定义: 并且它们的生成函数[4]可以表示为 Berg等[5]通过生成函数推导出以下矩量积分恒等式: Cao等[6]推导出了以下矩量积分恒等式: 引理1对于X∈N0且s/r=q-X,如果max{|at|,|bt|,|ar|}<1,有 引理2[7]对于X∈N0且s/r=q-X,如果max{|at|,|bt|,|ar|,|aw|,|bw|}<1,有 延续以上的成果,我们继续探索矩量积分以及它的应用,给出了下面两个主要结果. 注1在定理1和定理2中,令w=0,式(5)和(6)分别变为式(3)和(4). 下文将首先介绍一些相关的引理,给出定理1和定理2的证明过程.然后利用这两个定理推出两个广义的Rogers-Szegö多项式、Hahn多项式和Al-Salam-Carlitz多项式的生成函数并给出推理过程. 两个q-指数算子T(bDa)和E(bθa)[8]为 其中两个q-差分算子Da和θa分别为 引理3[4]假设f(a,b)是一个含有两个参数的函数且(a,b)=(0,0)∈C2. i)如果函数f(a,b)满足差分方程 bf(aq,b)-af(a,bq)=(b-a)f(a,b),(7) 则可以得到 f(a,b)=T(bDa){f(a,0)}. ii)如果函数f(a,b)满足差分方程 af(aq,b)-bf(a,bq)=(a-b)f(aq,bq),(8) 则可以得到 f(a,b)=E(bθa){f(a,0)}. 定理1的证明式(5)右边部分可以化为 其中 可以证明式(10)满足式(7),因此式(9)可化为 F(t,w)=T(wDt){F(t,0)}= 式(5)证毕. 定理2的证明式(6)右边部分可化为 其中 可以验证式(12)满足式(8),因此式(11)可化为 F(u,w)=E(wθt){F(u,0)}= 式(6)证毕. Rogers-Szegö多项式的生成函数在q-级数中非常重要,可以采用多种巧妙的方法[9-17]推导出来.Cao等[6]用矩量积分推导出以下两个混合式的广义Rogers-Szegö多项式的生成函数: 下文利用矩量积分推导出以下两个广义Rogers-Szegö多项式的生成函数. 注2特别地,在定理3中 令l=0,式(14)可化为式(13). 证明利用式(2)中Rogers-Szegö多项式的表示方法,式(14)的左边可改写为 利用式(5),式(16)等于式(14)的右边部分.同样地,式(15)的左边部分可改写为 式(17)等于式(15)的右边部分.证毕. 在这一部分,为得到结论,需要以下几个注解和定理. 根据文[2,11,15,18],Hahn多项式可被定义为 与它们相关的生成函数有 注3特别地,令t=0,式(20)和(21)可化为式(1). 现在,给出以下二元生成函数. 注4特别地,在定理5和定理6中,令m=0,x=1,a=0,s=0,式(22)和(23)可化为式(19). 证明利用式(18)中Hahn多项式的表示方法,式(22)的左边部分可改写为 利用式(5),令b=1,式(25)等于式(22)的右边部分.同样地,式(23)和(24)的左边也可以分别改写为 利用式(5)和(6),令b=1,分别可得到式(23)和(24)的右边部分.证毕. Al-Salam-Carlitz多项式[2]表示为 Al-Salam-Carlitz多项式是很重要的q-正交多项式,在许多领域有不同的应用,例如q- 谐波振荡器、θ函数、量子群和编码理论等.广义的Al-Salam-Carlitz多项式Un(x,y,a|q)和Vn(x,y,a|q)可被定义为 命题1[20] Al-Salam和Carlitz根据Rogers-Szegö多项式定义的两个离散分布的矩量dα(a)(x)和dβ(a)(x)也可表示为 其中二元的Rogers-Szegö多项式可表示成 Cao推导出的关于矩量积分和Al-Salam-Carlitz多项式之间的关系如下: 根据以上结果,现在给出以下二元生成函数: 注5特别地,在定理8和9中,令m=0,x=0,y=0,a=1,s=0,式(28)和(29)可化为式(26). 定理10 注6特别地,在定理10中,令m=0,x=0,y=0,a=1,s=0,式(30)可化为式(26). 证明利用式(27)中Al-Salam-Carlitz多项式的表示方法,式(28)的左边部分可改写为 根据式(6),式(31)等于式(28)的右边部分.同样地,式(29)和(30)的左边部分也可以被改写为 利用式(5),可分别得到式(29)和(30)的右边部分.证毕.

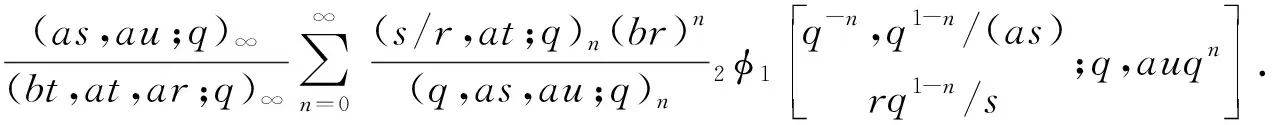
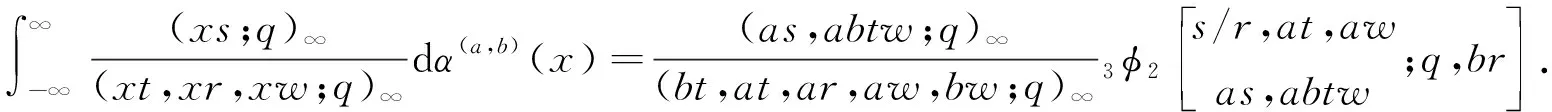
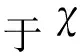
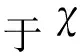

1 一些引理以及证明过程

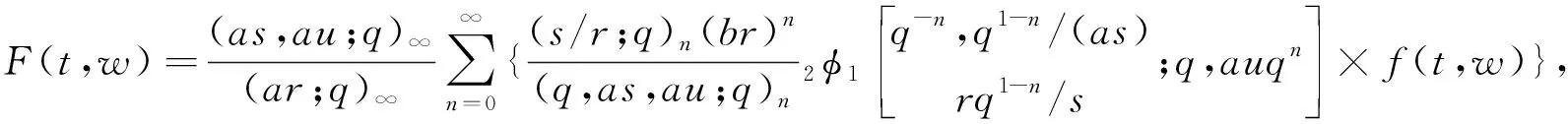
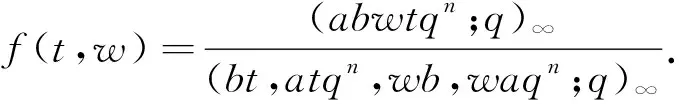


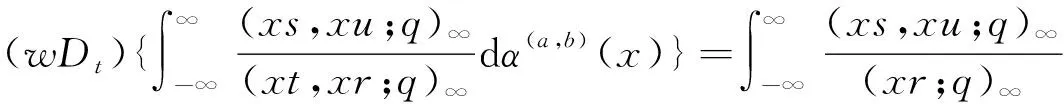



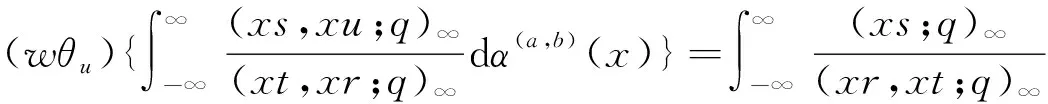
2 广义Rogers-Szegö多项式的两个生成函数


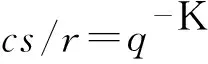



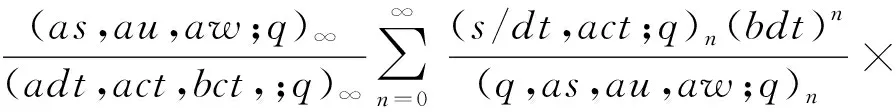

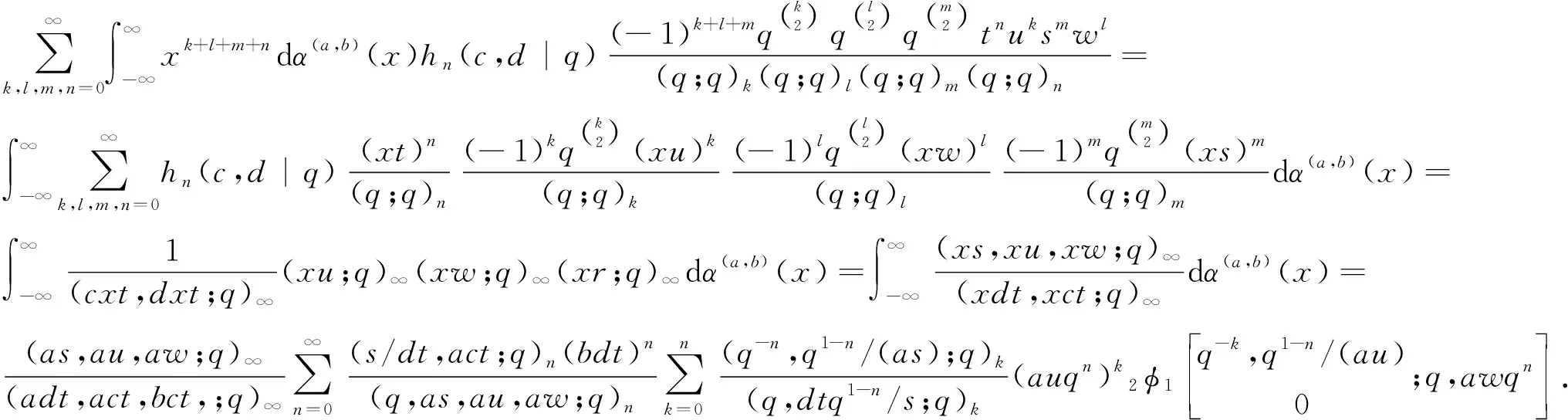
3 Hahn多项式的生成函数



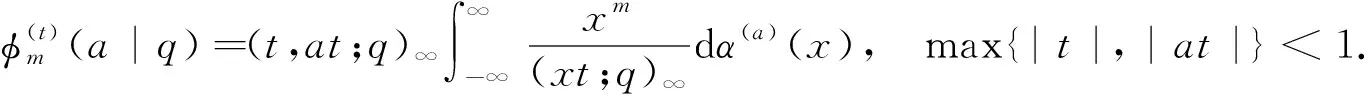
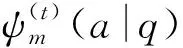

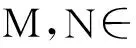
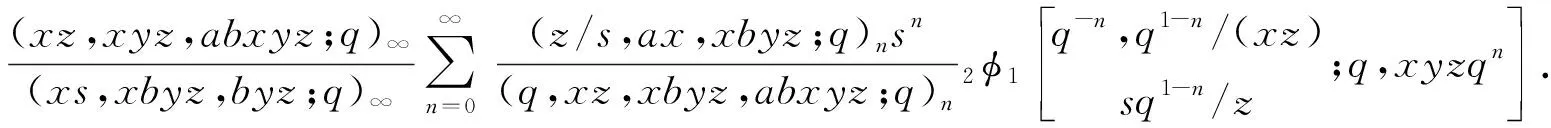
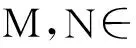

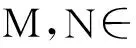

4 Al-Salam-Carlitz多项式的生成函数