一类中立型积分微分方程的概周期解*

刘怡建

(福州理工学院计算与信息科学学院数学系，福建 福州 350108)

1 问题的提出

周期解存在性的研究，是泛函微分方程定性理论分析中的一个重要部分，受到学术界的高度关注.由于在实际问题中滞后现象总是存在的，因此人们描述自然现象时，采用具有无穷时滞的中立型泛函微分方程比积分微分方程更客观.对于具有无穷时滞的泛函微分方程的周期解和概周期解的存在性问题，众多学者对它进行了研究[1-13].例如，方聪娜等[10]研究了如下一类具有无穷时滞的中立型Volterra积分微分方程的概周期解问题：

陈凤德等[11]讨论了如下周期系统的周期解的存在性和唯一性：

张志信等[12]在文献[11]的基础上，得到了如下中立型微分系统的周期解的存在性和唯一性的一组充分性条件：

林华远等[13]在文献[12]的基础上讨论了如下中立型概周期微分方程的概周期解的存在性和唯一性：

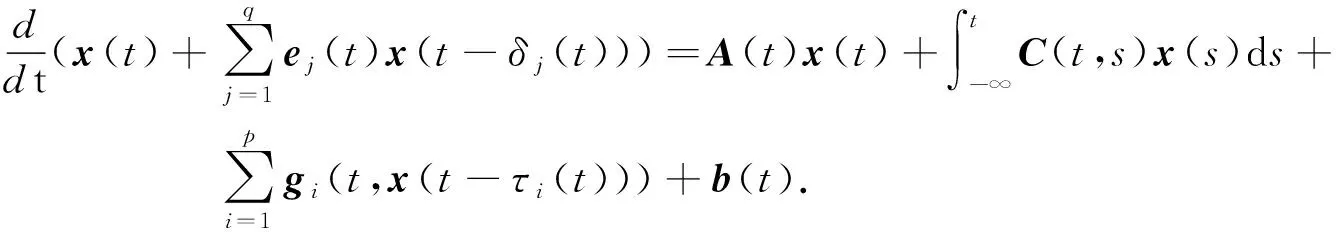
(1)

受这些文献的启发，笔者拟探讨比方程(1)更广泛的一类中立型积分微分方程的概周期解的存在性和唯一性.

2 预备知识

定义1[14]称f(t)是概周期的，如果对于∀ε>0，集合

T(f,ε)={τ;|f(t+τ)-f(t)|<ε,∀t∈R}

是相对稠密的.即对于∀ε>0，存在l=l(ε)>0，使得在每个长度为l的区间内至少有1个τ=τ(ε)∈T(f,ε)，满足|f(t+τ)-f(t)|<ε，t∈R.

定义2[14]若存在投影方阵P(P满足P=P2)及常数α≥0，β≥1，满足

‖X(t)PX-1(s)‖≤βe-α(t-s)t≥s，

‖X(t)(I-P)X-1(s)‖≤βeα(t-s)t≤s，

则称系统

x′=A(t)x

(2)

在R上具有指数型二分性.其中：x∈Rn；A(t)是定义在R上的分段连续的n×n实函数矩阵；X(t)是系统(2)的标准解方阵.

引理1[14]若线性系统(2)满足指数型二分性，则概周期系统

x′=A(t)x+g(t)

(3)

有唯一概周期解x(t)，

(4)

记ρ(x)是权函数，U是所有权函数构成的集合，ρ(t):R→(0,+∞)，ρ(x)在R上局部可积且ρ(t)>0.对于∀r>0,ρ∈U，记

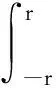
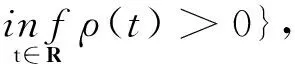
BC(R,Rn)是从R到Rn的有界连续函数，且范数定义为

3 主要结果及其证明

给出如下中立型积分微分系统：

(5)

其中：x∈Rn;t∈R;A(t)=(aij(t))n×n,C(t,s)=(cij(t,s))n×n,B(t,s)=(bij(t,s))n×n，都是R×R上的n×n函数矩阵；τi(t),δj(t)在R上连续；gi:R×Rn→Rn连续；ej(t):R→Rn×n连续；b(t):R→Rn连续.

引理2[11]设C(t,s)是关于(t,s)的n×n连续概周期函数矩阵，且满足如下条件：

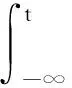
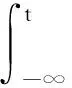
对于系统(5)，作如下假设：

(H1)A(t)，ej(t)关于t是概周期的，其中j=1,2,…,q.

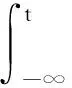
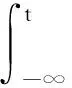
(H5)若gi(t,x)(i=1,2,…,p)关于t是概周期的，且gi(t,x)符合Lipschitz条件，则存在li>0，使得对于∀x,y∈Rn，有|gi(t,x)-gi(t,y)|≤li|x-y|.

定理1(ⅰ)假设(H1)～(H5)成立；

(ⅱ)线性系统x′(t)=A(t)x(t)满足投影为P和常数为β,α的指数型二分性；

若上述条件满足，则系统(5)存在唯一的概周期解x(t).

对于∀u∈B,考察如下积分微分方程：

(6)

令

则方程(6)转化为

(7)

其中

由假设(H1)～(H5)及引理2易知h(t)是连续概周期的.

设X(t)为系统(3)的基本解矩阵，则由假设(H1)～(H5)及引理1可知方程(7)有唯一概周期解D(t)，

从而

(8)

是系统(5)的唯一的概周期解.证毕.

定义算子T:B→B为Tu(t)=xu(t),∀u∈B.现证明T:B→B是一个压缩映射.事实上，对于∀u,v∈B,由(8)式及条件易知

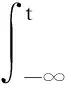
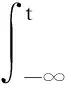
即

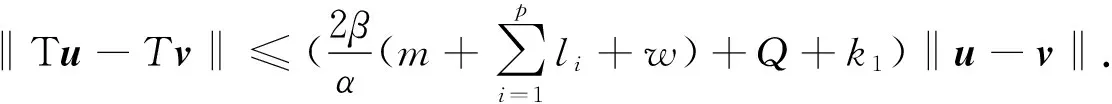
系统(5)可以推广到如下概周期系统：

(9)

定理2(ⅰ)假设(H1)～ (H5)成立；

(ⅱ)线性系统x′(t)=A(t,u(t))x(t)满足投影为P和常数为β,α的指数型二分性，且二分常数β,α不依赖于u(t)，其中u(t)是任意连续概周期的；

若上述条件满足，则系统(9)存在唯一的概周期解x(t).

证明过程类似于定理1.

注1当B(t,s)=0时，系统(5)为文献[13]中研究的系统，因此本研究是文献[13]的推广.