基于观测器的多智能体系统的有限时间包含控制

张静怡， 苗国英, 2， 纪 龙

(1.南京信息工程大学 自动化学院,南京 210044；2.南京信息工程大学 江苏大气环境与装备技术协同创新中心，南京 210044)

0 引言

近年来，由于在无人机编队、机器人聚集等领域的广泛应用，多智能体系统的分布式协同控制已成为控制领域[1-2]的热点问题，其主要研究方向有：一致性问题[3]、群集问题和编队问题[4]等。早期对多智能体系统的研究工作，主要集中无领导者和单领导者的拓扑结构，然而在多智能体实际应用中，由于单领导者能力有限，往往需要多个领导者来实现集体层面上的协同合作。当系统中存在多领导者的情况时，文献[5]为使跟随者移动至领导者组成的给定几何空间中，提出包含控制问题。

包含控制可以看作编队问题的特殊情形，是指通过设计分布式控制器，驱使一组跟随者在多个领导者的引领下, 最终进入并保持在由领导者所形成的几何空间(凸包)中运动。与传统多智能体的一致性问题相比，包含控制更能突出分布式协同控制的优势，因此包含控制问题得到国内外学者的广泛研究。对于高阶多智能体系统，文献[6]考虑了在连续和离散时间的情况下，基于相邻智能体输出信息的包含控制问题。文献[7]考虑基于马尔科夫切换的通信拓扑下，作者提出带有测量白色噪声的包含控制方法。文献[8]针对带有静态和动态领导者的多智能体系统，考虑输入延迟问题，基于脉冲控制算法理论，提出一类基于脉冲通信周期的包含控制算法。文献[9]考虑基于系统的状态反馈量和输出反馈量设计包含控制协议，得到多智能体系统在输入饱和状态下达到包含控制的充分条件。针对离散时间系统，在无向固定通信拓扑下，文献[10]实现包含控制的收敛时间根据任务要求预先设定。在文献[11]中，考虑带有通信噪声的多智能体系统，基于卡尔曼滤波理论，作者设计一种随机包含控制协议。目前已有的多智能体系统包含控制算法，大多是基于渐近稳定性理论[12]，即各个智能体在时间趋于无穷大时达到理想状态。为提高系统的控制精度，进而提出有限时间控制算法，既提高了系统的收敛速度，又可以增强控制器的鲁棒性。文献[13]引入非线性反馈控制方程，通过线性矩阵不等式，得到了系统实现有限时间包含控制的充分条件。文献[14]研究了二阶系统基于跟随者的相对状态，在固定拓扑下的有限时间包含控制问题。

在有向图通信拓扑下，本文研究了具有一般形式的多智能体有限时间包含控制问题，利用终端滑模控制良好的鲁棒性，可使系统状态在有限时间收敛到平衡点，突破了传统系统渐近收敛的局限。与文献[13]相比，本文考虑了二阶系统的情况，并针对跟随者状态不可在线获得的问题，提出一种基于有限时间状态观测器的算法。与文献[14]相比，本文引入快速终端滑模控制，并考虑具有未知有界加速度的领导者情况，可在保持传统滑模控制优点的前提下，有效加快系统收敛速度且更具有实际应用意义。本文提出了两类有限时间控制算法，利用模型转换的技巧，把包含控制问题转化为系统的稳定性问题。基于李雅普诺夫理论、图论、线性矩阵不等式的技巧，得到使系统达到包含控制的充分条件，最后通过仿真，验证算法的有效性。

1 图论及相关引理

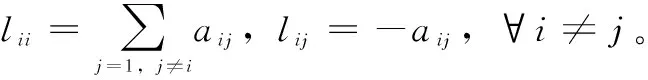
在给出本文的主要定理之前，先引入一些重要的引理和假设条件。

假设1：在多智能系统中，对于任意跟随者智能体，领导者至少存在一条通往该跟随者的有向路径。

引理1[15]：对于如下多智能体系统，假设存在一连续正定的函数V(x)定义在原点的邻域，且满足实数c>0,a∈(0,1)，使得：

1)V(x)是正定的；

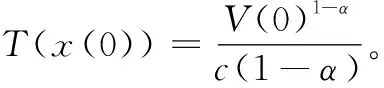
2 有限时间包含控制

本文考虑由M个跟随者和N-M个领导者组成的有外部干扰的多智能体系统，有向图G= (V,E,A)表示系统的通信拓扑结构。在实际的系统中，单个无人艇看作是一个智能体，由于传统单无人艇存在执行任务能力单一、鲁棒性差等问题，多无人艇协同控制技术已在海洋环境中得到广泛应用。例如，M艘跟随艇和N-M艘领航艇组成的多无人艇系统，控制目标是通过设计无人艇控制器算法驱使跟随艇在有限时间内达到期望的位置和速度，并收敛到由领导者组成的凸包中。多无人艇系统由领航艇和跟随艇组成，领航者具有自主完成任务的行为，跟随者具有通信信息交互和追踪领航者行为。

由于考虑领导者不与其它领导者通信的情况，因此图G的拉普拉斯矩阵可以写成如下形式：

式中，F={1,…,M}和R={M+1,…,N}分别表示跟随者和领导者所在的集合，LFF∈RM×M,LFR∈RM×(N-M)。

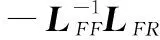
考虑跟随者的二阶动力学模型描述如下：

(1)

其中：xi∈Rn,vi∈Rn分别表示第i个跟随者智能体的位置状态和速度状态，ui∈Rn表示第i个跟随者智能体的控制输入，ωi∈Rn为外部干扰及不确定项。

考虑领导者的二阶动力学模型描述如下：

(2)

其中：xi∈Rn,vi∈Rn,ui∈Rn分别表示第i个领导者智能体的位置、速度和控制输入。

针对带有多个领导者的多智能体系统，本文基于快速终端滑模控制设计有限时间包含控制算法。首先引入闭环位置和速度包含误差系统设计终端滑模面；其次基于设计的滑模面，分别构造领导者和跟随者的有限时间包含控制协议，该包含控制算法能有效抑制外部干扰，使系统表现出更好的鲁棒性。

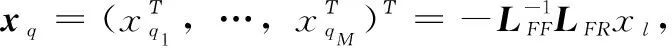
exi=xfi-xqi,i=1,…,M

evi=vfi-vqi，i=1,…,M

(3)

根据系统位置误差和速度误差方程式(3)，定义滑模面为：

Si(t)=(exi(t))q/p+evi(t)

(4)

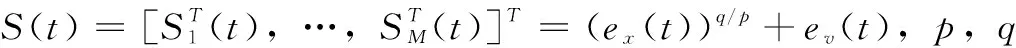
针对系统式(1)、(2)，基于快速终端滑模控制的思想，提出分布式控制算法如下：

ui(t)=

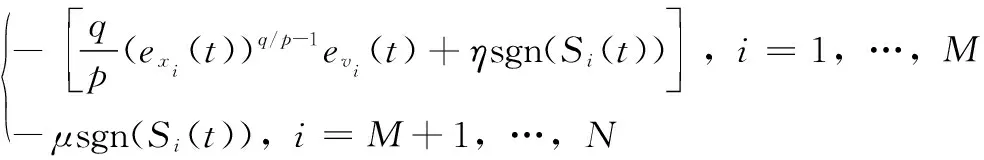
(5)

定义1[13]：对于有限时间T∈(0,+∞)，若系统满足对智能体任意初始状态x(0)，跟随者式(1)都能移动并保持在由领导者式(2)组成的凸包中运动，则称控制协议(4)、(5)能在T时刻内解决系统的有限时间包含问题，表示如下式：

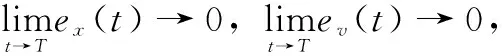
定理1：对于带有外部干扰的多智能体系统，假设通信拓扑图G具有有向生成树且满足假设1，若存在常数η>0，则在协议(4)、(5)作用下，多智能体系统(1)、(2)可实现有限时间包含控制。

其中：uf(t)=[u1(t),…，uM(t)]Τ。

3 基于观测器的有限时间包含控制

上述内容研究基于滑模面的有限时间包含控制问题，其中跟随者的位置和速度信息都可以在线获得。下面进一步考虑静态多领导者系统中，跟随者状态不能在线获得的情况。考虑跟随者是较为一般的系统模型[17]如下：

(6)

考虑领导者的系统模型为：

(7)

其中：A∈Rn×n，B∈Rn×p，C∈Rq×n表示维度相容的输入和输出矩阵，xi(t)∈Rn，ui(t)∈Rp，yi(t)∈Rq分别表示在t时刻，第i个智能体的状态、控制输入和输出。

假设2:在线性多智能体系统(6)中，A为Hurwitz矩阵且(A,B,C)为可镇定且可检测的。

由于在实际应用系统中，领导者的状态可知，跟随者需要根据相邻智能体之间的信息交互来更新自身状态信息，考虑由于通信时延、环境噪声干扰等因素的影响，跟随者不能在线获得相邻智能体状态的情况，因此本文为每个跟随者智能体设计状态观测器，如式(8)所示：

(8)

sig(y)α=(|y1|αsgn(y1),…,|yk|αsgn(yk))Τ,α>0

其中：|yi|表示yi的绝对值，sgn(·)表示符号函数，y=(y1,y2,…,yk)Τ,i=1,2,…,k。

受到文献[13]启发，对于第i个跟随者智能体，基于上述观测器设计分布式有限时间控制协议如下：

(9)

其中：k>0，ε>0为常数，0<γ<1，P为满足式(10)的正定矩阵。

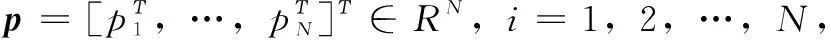
pΤsig(p)α≥(pΤp)(1+α/2),α∈(0,1)

在假设2成立的情况下，矩阵A为Hurwitz矩阵，对于矩阵P>0，满足下列不等式：

PA+AΤP-ελmin(LFF)PBBΤP<0

(10)

其中：λmin(·)表示矩阵的最小特征值。

定理2:考虑带有多个领导者的多智能体系统，满足假设1～2且通信拓扑图G具有有向生成树，对于任意的正实数β，矩阵P>0满足式(10)，则在算法(8)、(9)的作用下能使系统(6)、(7)在有限时间实现包含控制。

证明：定义每个智能体系统状态和观测器状态之间的误差ei(t)为：

(11)

(12)

定义每个跟随者智能体包含控制误差向量δi(t)为：

(13)

将式(12)整理成如下增广矩阵形式：

(14)

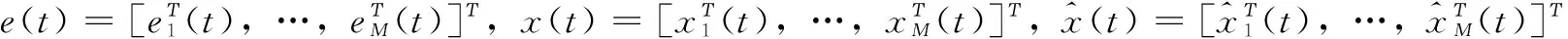
选定Lyapunov函数V1(t)=e(t)Τe(t)，沿着系统(14)的轨迹求(t)关于时间t的导数，并将式(12)代入，则有:

2e(t)T(IM⊗A)e(t)-2e(t)TβCTGTsig[(IM⊗GC)e(t)]a

考虑A为Hurwitz矩阵，且e(t)T(IM⊗A)e(t)<0，由引理3可得：

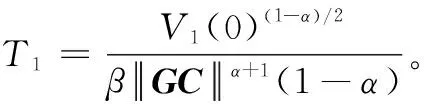
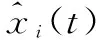
ε(LFF⊗B)sig[(I⊗P)δ(t)]γ

选定Lyapunov函数V2(t)=δΤ(t)(I⊗P)δ(t)，根据上式，对V2(t)求导可得：

2εδΤ(t)(I⊗P)(LFF⊗B)sig[(I⊗P)δ(t)]γ

由引理2和3可知，矩阵LFF的所有特征值均具有正实部，且正定矩阵P满足式(10)的矩阵不等式，如下形式：

I⊗(PA+AΤP)-ελmin(LFF)(IN⊗PBBTP)<0

其中：λmin(LFF)表示LFF矩阵的最小特征值。

于是满足下式：

4 仿真结果与分析

为验证本文所提算法的有效性，给出以下的仿真示例。本文针对实际应用中多无人艇系统，考虑复杂多变的海洋环境和通信环境，多无人艇系统需要适应各类不确定因素，同时也要高效完成协同控制任务，对多无人艇有限时间包含控制问题进行仿真。

假设多无人艇系统具有3个跟随艇和3个领航艇，其中无人艇1,2,3为跟随者，无人艇4,5,6为领导者，图1为系统的有向通信拓扑图。

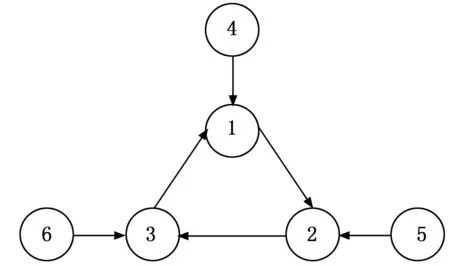
图1 无人艇通信拓扑结构

由图1可知，系统的邻接矩阵、Laplacian矩阵分别如下：

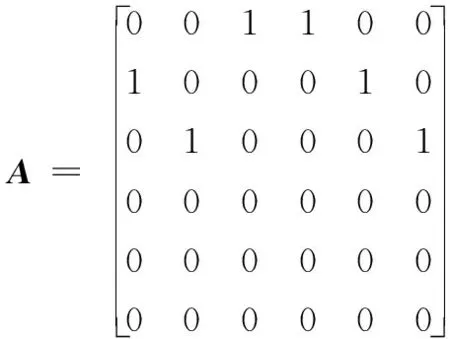
选取无人艇控制器的参数为p=7,q=5,η=10，μ=0.1。假设各艘跟随无人艇受到的未知海洋环境干扰为ωi=[0.1sin(t),0.1cos(t)]Τ,i∈1,2,…,M。各艘无人艇的初始状态坐标分别为(-7,10)、(9,7)、(-13,-9)、(-2,6)、(5,4)、(-3,-2)。

根据定理1，利用算法(4)、(5)，多无人艇系统(1)、(2)的状态可实现包含控制。图2表示滑模面随时间变化的曲线，仿真结果表明滑模面在2.5 s时到达S(t)=0。图3表示领航艇和跟随艇的运动轨迹，跟随艇航迹在4 s后完全收敛并保持在由领航艇航迹组成的凸包中运动。

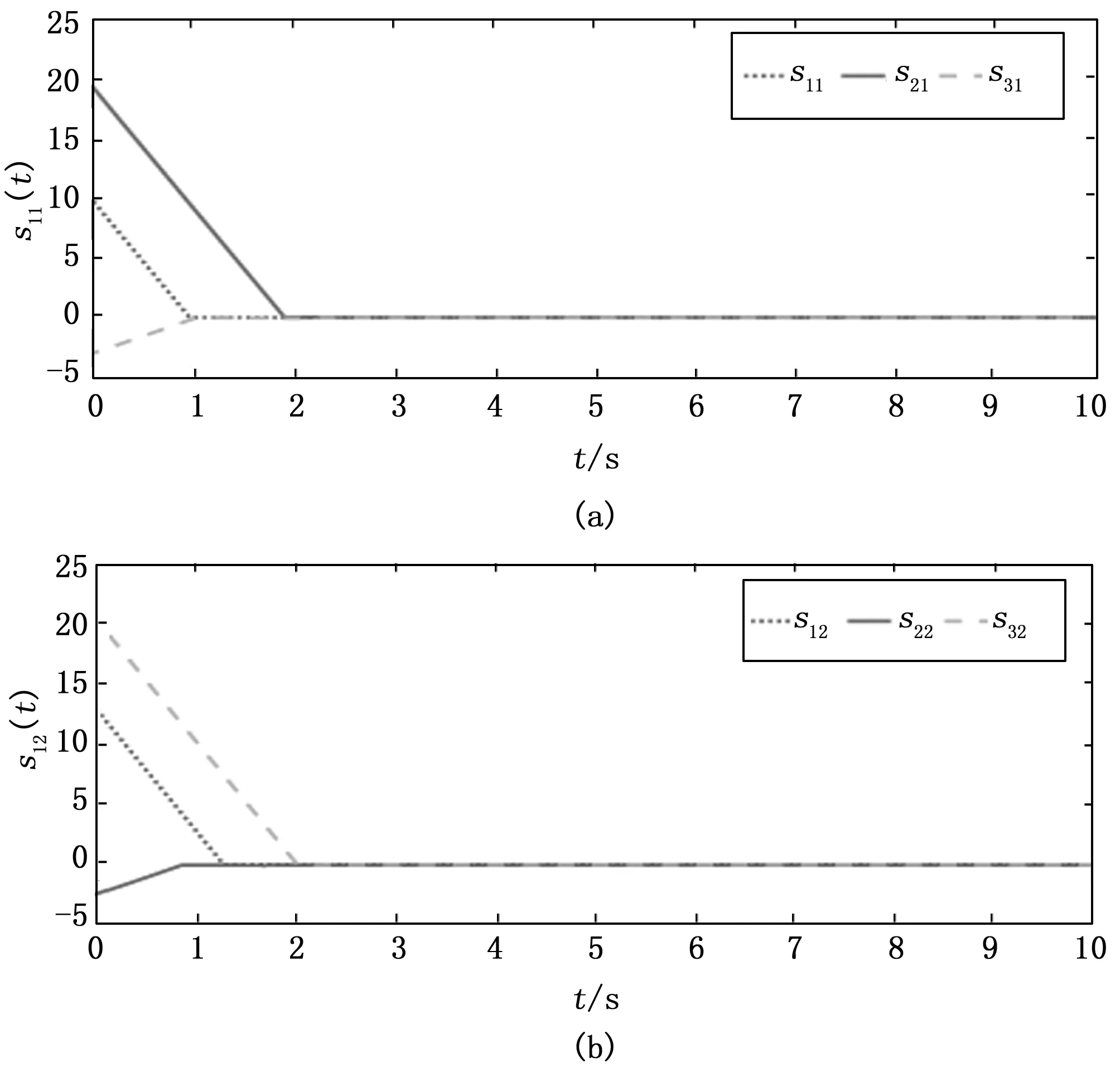
图2 滑模面变化轨迹

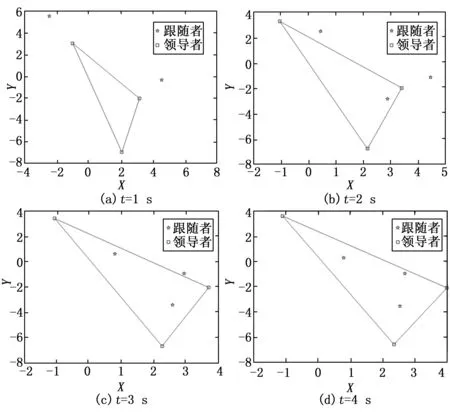
图3 无人艇运动轨迹

假设基于状态观测器的无人艇系统参数选取为：

通过Matlab工具箱求解线性矩阵不等式(10)，得到矩阵P的可行解为：

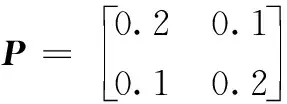
根据定理2，利用控制算法(8)、(9),多无人艇系统(6)、(7)的状态可以实现包含控制，通过计算，得到T1=3.7 s，T2=2.63 s，时间上限为T1+T2=6.33 s,仿真结果如图4和图5所示。图4表示每艘跟随艇状态误差随时间变化曲线，在2.5 s时系统状态估计值与真实值达到一致。图5表示各无人艇位置状态随时间变化的轨迹曲线,仿真显示在1.5 s时，跟随艇进入由领航艇形成的凸包内，在有限时间6.33 s内达到包含控制。通过对多无人艇包含控制仿真结果与分析，表明本文理论结果的有效性。

图4 误差变化轨迹

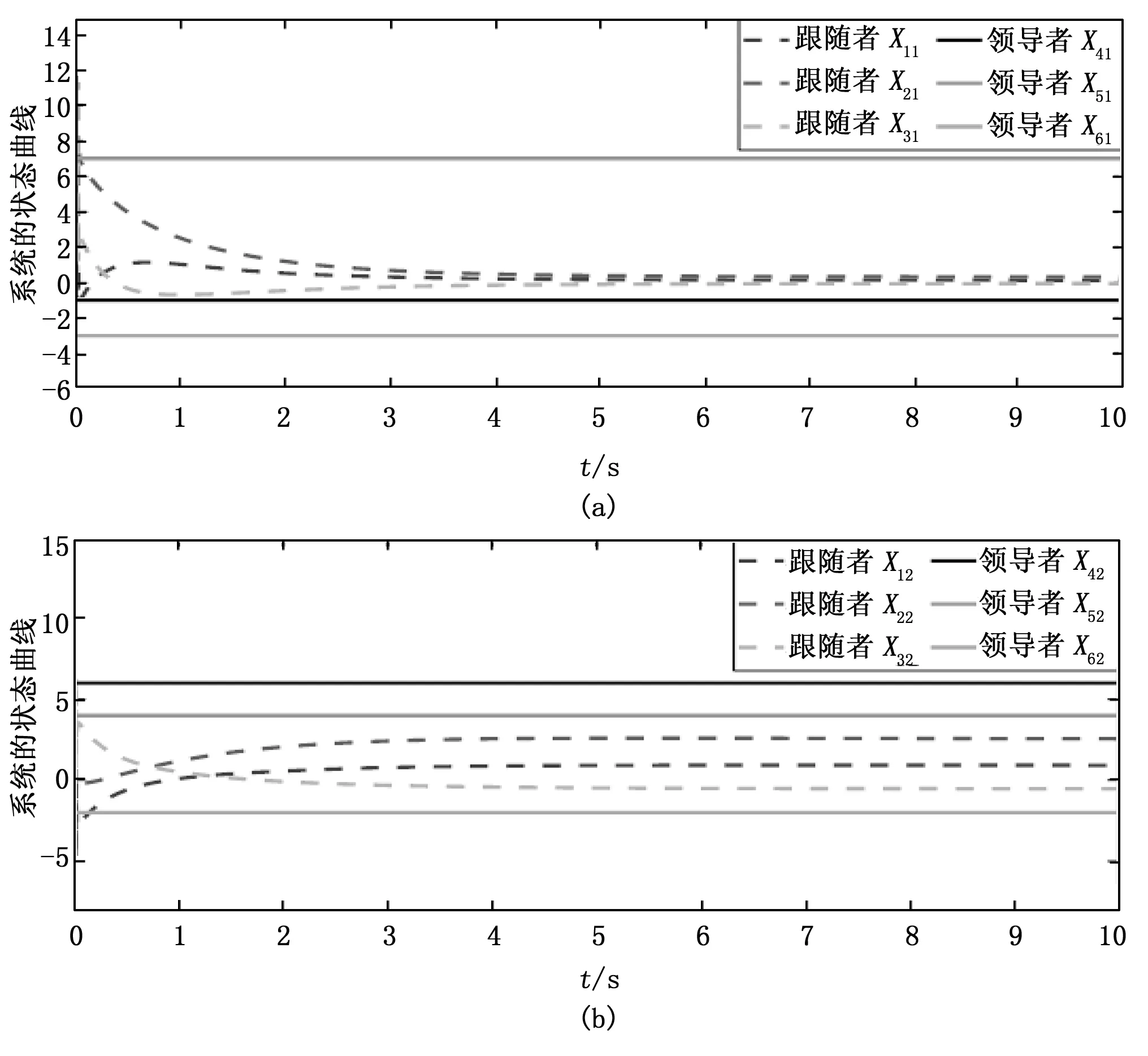
图5 无人艇各方向运动轨迹

5 结束语

本文针对多智能体系统，提出基于快速终端滑模控制的有限时间包含控制算法，运用图论、李亚普诺夫稳定性理论和非线性系统理论，得到实现包含控制的条件。进而，对于一般形式的多智能体系统，考虑基于输出信息构造有限时间状态观测器，即在有限时间内估计出智能体的运动状态，解决了智能体运动状态不可在线获得的问题。此外，当通信中存在噪声干扰和随机变化的拓扑情况，研究多智能体系统的包含控制问题，是下一步的主要研究工作。