二阶非匹配非线性多智能体系统的自适应滞后一致性控制

游秀，王帅，贾新春

（山西大学 数学科学学院，山西 太原 030006）

0 引言

近年来，多智能体分布式协调控制在很多领域受到了广泛关注［1—5］，这其中包括多机器人系统控制、无人车的编队控制、大规模传感器网络的自主配置、航天器深空探测等。从控制目标角度来讲，多智能体协调控制的研究主要包括聚结［6］、会合［7］、编队［8］和一致性［9］。其中，一致性是多智能体系统的核心问题，也是目前多智能体研究的热点之一。

一致性控制是指通过设计合适的控制协议使系统中各智能体的状态量随着时间的推移最终趋于相同。目前，多智能体系统一致性问题的研究已经取得了许多成果［10—15］。文献［10］研究了不确定通信环境中一阶离散时间多智能体网络的平均一致性问题。文献［11］通过线性变换解决了高阶连续线性多智能体系统的一致性问题。文献［12］通过设计一种基于采样数据控制和边缘事件驱动技术的一致性协议，解决了无向拓扑下多个双重积分器网络的一致性问题。文献［13］基于静态反馈提出了一种完全分布式的一致性算法，解决了有向图下由多个积分动力学描述的高阶多智能体系统的一致性问题。文献［14］基于位置、速度和加速度三者的测量误差，设计了一个新颖的事件触发控制机制，分析了三阶离散多智能体系统的一致性问题。文献［15］则利用分布式控制方法，解决了切换网络下异构二阶非线性不确定多智能体系统的一致性问题。此外由于智能体间通过网络来进行信息传递，网络时延、网络带宽有限等问题最终会导致控制器失效。为了解决这些问题，文献［16］基于事件的控制策略，研究了具有输入时延的多智能体系统的领导跟随一致性问题。在文献［17］中，通过频域分析方法，研究了具有时不变时滞的欧拉多智能体系统的领导跟随一致性问题。为了处理时变的通信延迟，文献［18］将前馈控制方法与自适应控制方法相结合设计了一种新的分布式自适应控制器。综上所述，这些研究仅针对信息传递过程中的通信时延对一致性产生的影响，提出了一系列控制协议。然而，在实际的多智能体系统中，邻居智能体的一致性状态往往也是有时延的，即滞后一致性。在某些情况下，完全一致是有害的，需要避免；而滞后一致却是有益的。例如，公路上一定数量的车辆同时到达某个位置就可能引起塞车，如果它们在到达的时间上具有一个合适的时延则可有序通过，基于此，领导跟随多智能体系统的滞后一致性概念首次在文献［19］中被提出。此后，大量文献针对多智能体系统进行了滞后一致性的研究［20—22］。文献［20］研究了具有非线性动力学和切换拓扑的二阶多智能体系统的集群滞后一致性问题，提出了一种基于位置和速度测量的控制算法。文献［21］讨论了具有通信延迟和切换拓扑的多智能体系统领导跟随滞后一致性问题。文献［22］分析了基于牵制控制的二阶非线性多智能体系统的滞后一致性。然而，目前针对多智能体系统滞后一致性的研究主要集中在线性系统或匹配的非线性系统，并没有充分考虑到实际的多智能体系统中普遍存在的非匹配非线性特性，这限制了所提出结果的普适性。因此，考虑非匹配非线性多智能体系统的滞后一致性问题就显得尤为重要。

在本文中，我们考虑了具有未知干扰的非匹配非线性多智能体系统的领导跟随滞后一致性问题。本文的主要贡献概括如下：（1）考虑了二阶非匹配非线性多智能体系统的一致性问题，所考虑的系统可以更好地刻画实际系统；（2）将自适应方法与反步控制方法相结合，设计了新的控制器用来消除存在的非匹配非线性项和外部干扰，从而实现多智能体系统的领导跟随一致性；（3）针对二阶非匹配非线性多智能体系统，考虑了滞后一致性控制，这更符合实际的网络通信环境。

1 预备知识和问题描述

1.1 图论

我们用图G（ν，ε，A）表示智能体间的信息交互，其中ν＝{1，2，…，N}表示图节点的集合，ε＝v×u表示边集合，(i，j)∈ε表示节点i能接收到节点j的信息，则节点j被称为节点i的邻居。Ni＝{j∈u|(i，j)∈ε}表示节点i的邻居集。邻接矩阵A＝[aij]N×N，其中aii＝0，当(i，j)∈ε，aij＝aji＝1。与邻接矩阵A相关联的拉普拉斯矩阵L＝[lij]N×N满足，lij＝—aij其中i≠j，。用矩阵B来描述通信拓扑图G中可以直接接收到领导智能体状态信息的跟随智能体的情况，其定义B＝diag{b1，…，bN}为对角矩阵，当且仅当领导者与第i个跟随者有通信关系时，有bi＝1；否则bi＝0。

1.2 问题描述

考虑由一个领导者和N个跟随者组成的二阶非匹配非线性系统。第i个跟随者的动力学模型为

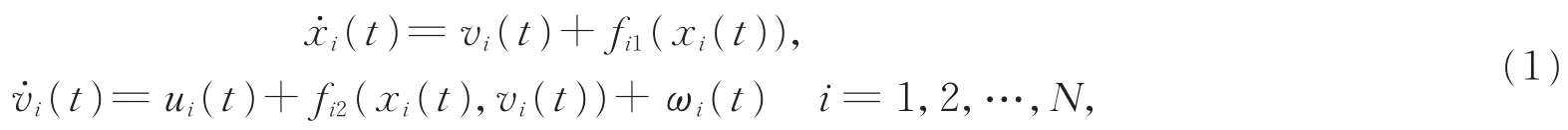
其中xi(t)，vi(t)∈Rn是状态变量，fi1(xi(t))，fi2(xi(t)，vi(t))∈Rn是未知的连续非线性函数，ui(t)∈Rn是控制输入，ωi(t)∈Rn是未知的外部干扰并且满足：存在未知常数δi，使得‖ωi(t)‖≤δi。

领导者的动力学模型为

其中x0(t)，v0(t)∈Rn是领导者的状态变量，f01(x0(t))，f02(x0(t)，v0(t))∈Rn是领导者的未知连续非线性函数。

在本文中我们假设所考虑的系统中的未知非线性函数满足以下条件。

假设对于i＝1，2，…，N，有

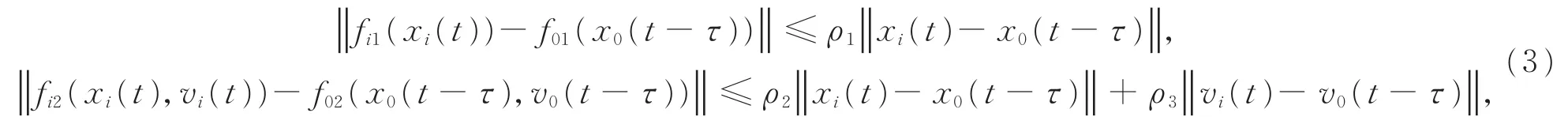
其中ρ1，ρ2，ρ3为非负常数。

根据滞后一致性的性质给出如下定义：若二阶多智能体系统(1)和(2)在任意初始条件下满足

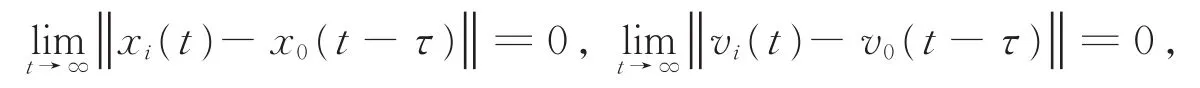
其中τ＞0为时滞常数，则称多智能体系统(1)和(2)能够实现领导跟随滞后一致性。

本文的研究目的是基于自适应控制思想设计分布式控制协议，使得带未知外部干扰的二阶非匹配非线性多智能体系统实现领导跟随滞后一致性。

2 二阶非匹配非线性多智能体系统滞后一致性控制

针对由(1)和(2)组成的多智能体系统的滞后一致性问题，设计了一种基于自适应控制方法和反步控制方法的分布式控制器。下面将进行详细讨论。

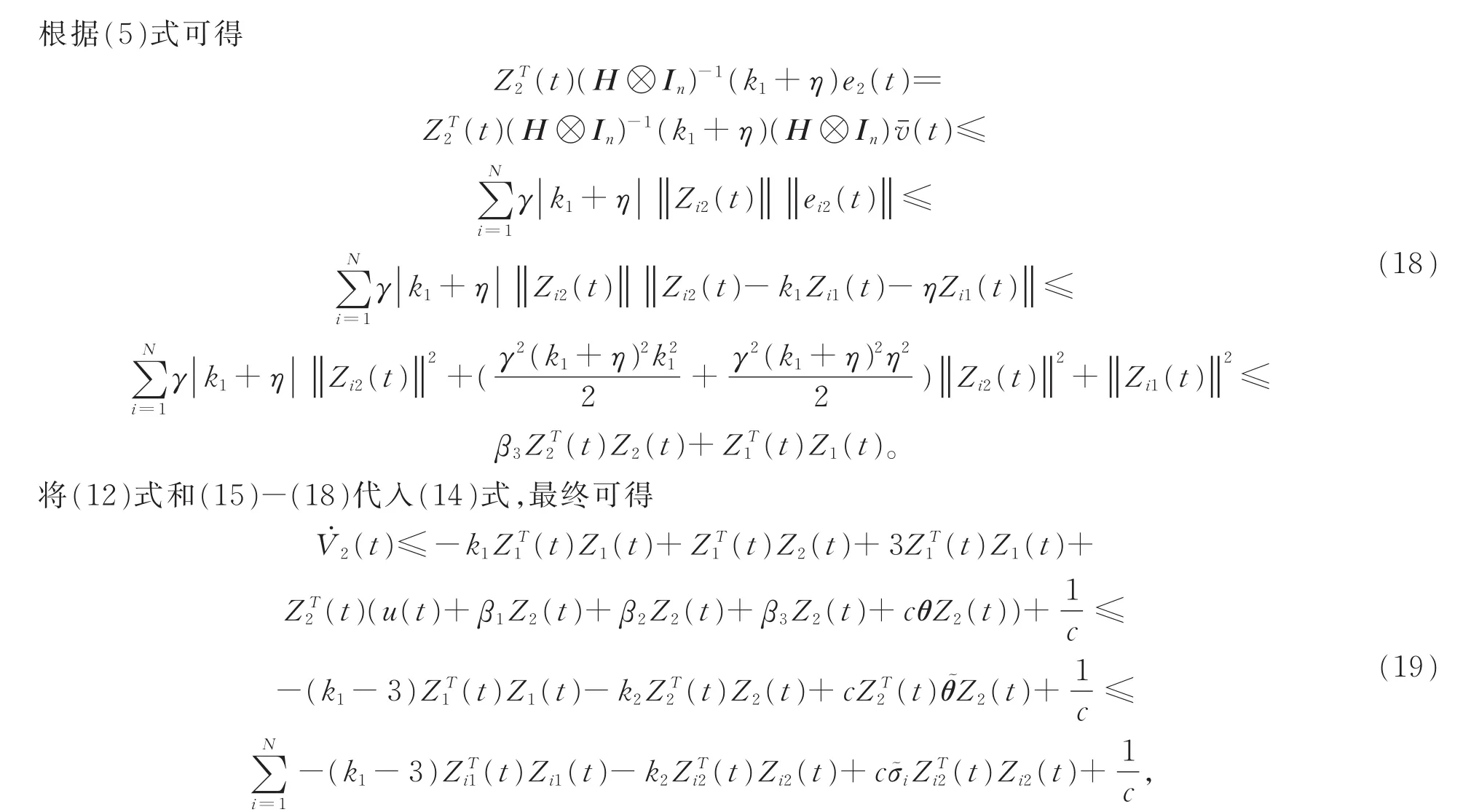
定理考虑由式(1)和(2)描述的带有时滞τ的二阶非匹配非线性多智能体系统，考虑其通信拓扑图为无向连通。如果设计分布式控制器为(12)和(13)，那么所考虑的多智能体系统能够达到领导跟随滞后一致性。

证明基于上述的讨论，构造系统的Lyapunov函数为V(t)＝V2(t)+V3(t)，设计V3(t)为

结合等式(13)和不等式(19)可得

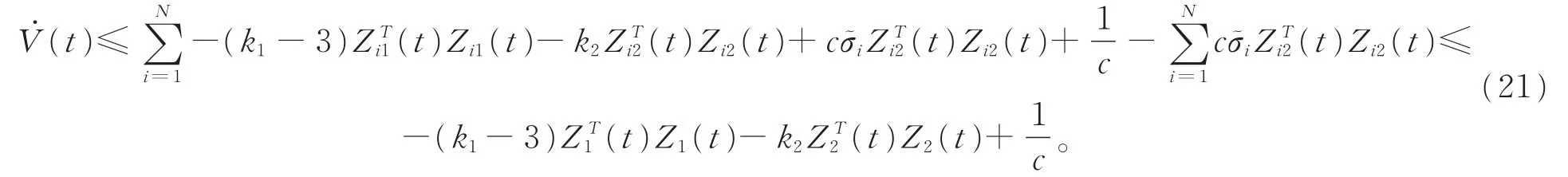
由于V(t)是正的以及k1＞3，根据(21)式可得当t→∞时，V(t)有界。因此，Z1(t)，Z2(t)是有界稳定的。可得Zi1(t)，Zi2(t)也是有界稳定的。因此是有界稳定的。这进一步说明了也是有界稳定的，因此可得e2(t)是有界稳定的。由于e1(t)＝Z1(t)，所以e1(t)也是有界的稳定。因为H＝L+B，根据(5)式可得(t)和(t)也是有界稳定的。从而完成了定理的证明。

3 数值仿真

在这一部分中，给出了一个例子来说明所提出的分布式自适应控制器的有效性。考虑由五个（一个领导者和四个跟随者）Chua电路组成的多智能体系统，其中ωi(t)＝sin(t)，

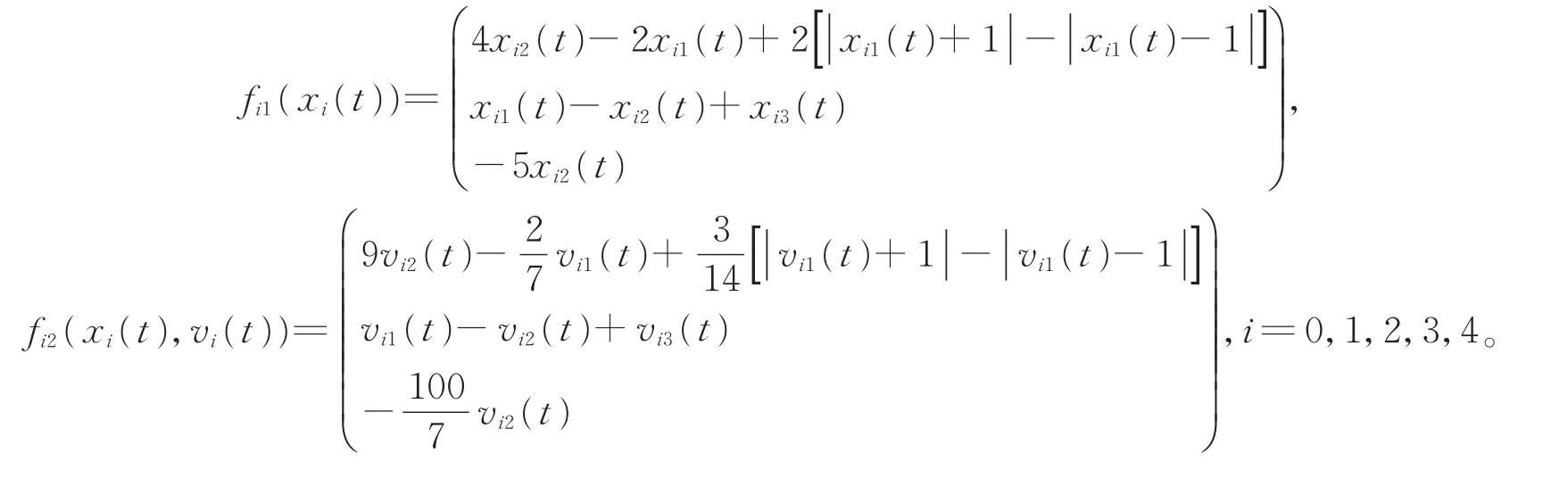
网络拓扑结构如图1所示。根据定理的证明过程可得第i个智能体的控制器ui(t)如(12)式所示，其中k1＝4，k2＝1，c＝22，ρ1＝10，ρ2＝0，ρ3＝16.975 4，α＝γ＝4.7913，μ＝1。选择系统中各变量的初始值为

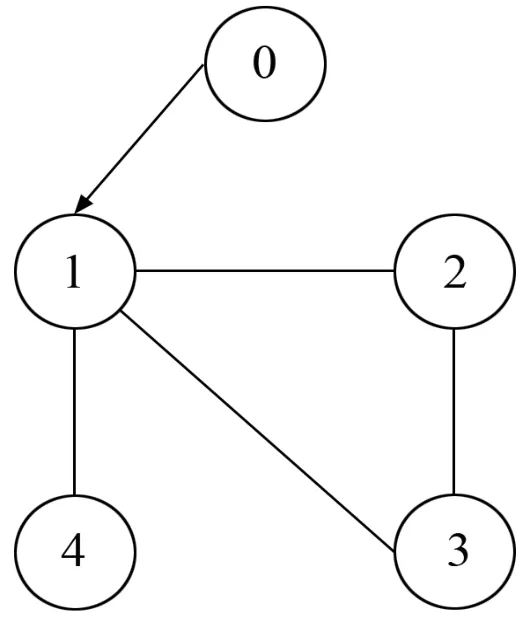
图1 智能体间的通信关系拓扑图Fig.1 Topology graph of communication relationship among agents

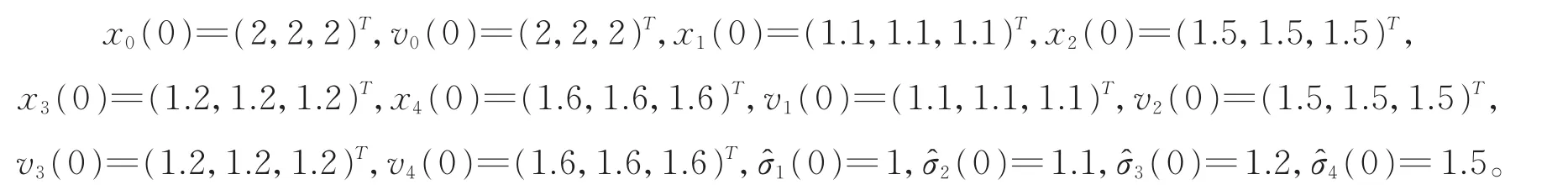
时延选择为τ＝1，那么，系统未知外部干扰的估计误差i的仿真曲线如图2所示。从图3—图8中可以明显看出所考虑的多智能体系统在图1所示的拓扑条件下能达到领导跟随滞后一致性。

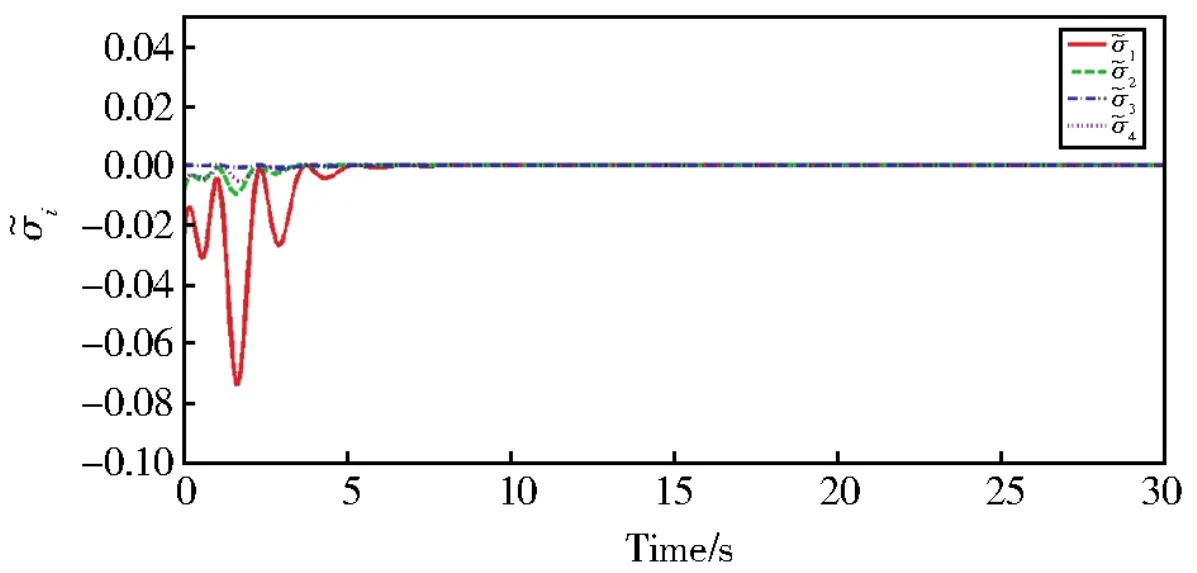
图2 外部干扰估计误差σ͂iFig.2 External disturbance estimation errors σ͂i

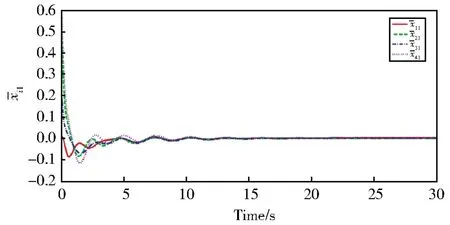
图3 领导者与跟随者第一个状态的第一个分量的滞后一致性误差i1(t)Fig.3 First component of first state′s lag consensus errors between leader and followersi1(t)

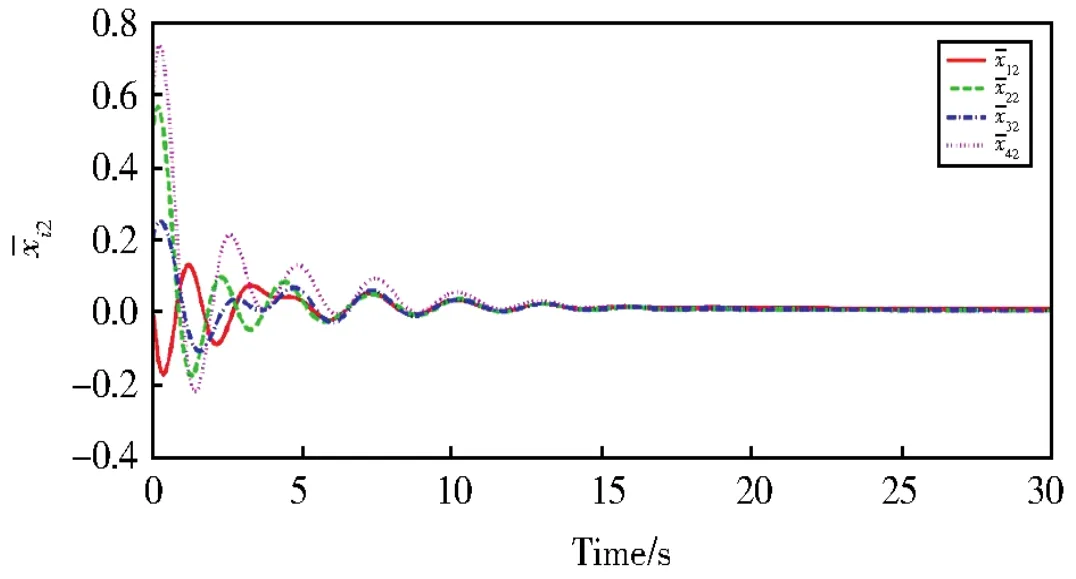
图4 领导者与跟随者第一个状态的第二个分量的滞后一致性误差i2(t)Fig.4 Second component of first state′s lag consensus errors between leader and followersi2(t)

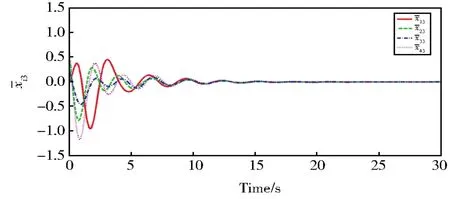
图5 领导者与跟随者第一个状态的第三个分量的滞后一致性误差i3(t)Fig.5 Third component of first state′s lag consensus errors between leader and followersi3(t)

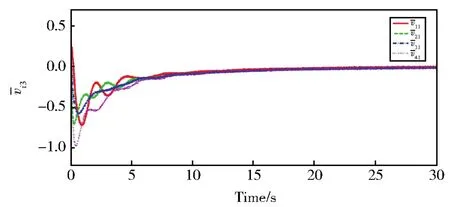
图6 领导者与跟随者第二个状态的第一个分量的滞后一致性误差i1(t)Fig.6 First component of second state′s lag consensus errors between leader and followersi1(t)

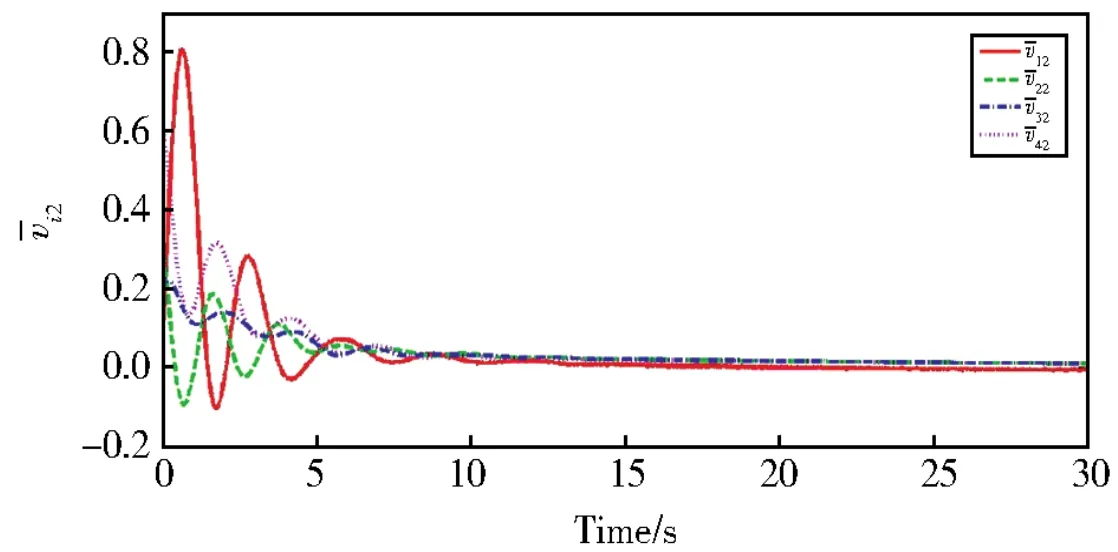
图7 领导者与跟随者第二个状态的第二个分量的滞后一致性误差i2(t)Fig.7 Second component of second state′s lag consensus errors between leader and followersi2(t)

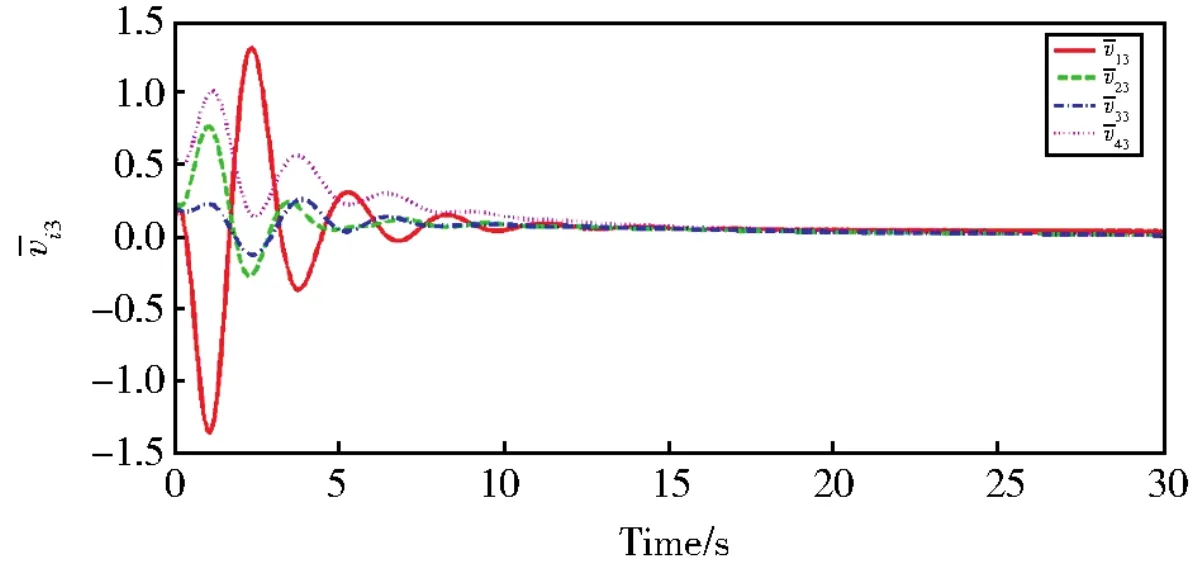
图8 领导者与跟随者第二个状态的第三个分量滞后一致性误差i3(t)Fig.8 Third component of second state′s lag consensus errors between leader and followersi3(t)

4 结论

本文考虑了具有未知干扰的二阶非匹配非线性多智能体系统的领导跟随滞后一致性控制问题。首先，在满足Lipschitz条件的基础上，设计了一种新的基于自适应控制方法的分布式控制器，在处理非匹配非线性项的同时，估计了未知外部干扰的近似误差。然后，利用李雅普诺夫稳定性理论证明了所有的一致性误差都是有界稳定的，即可以实现有界的领导跟随滞后一致性。最后，给出了一个仿真实例证明了所提出的理论结果。