含变点时HIV动力学模型的联合贝叶斯推断

齐培艳，刘俊俊，段西发

（太原科技大学 应用科学学院，山西 太原 030024）

0 引言

在HIV研究中，病毒载量和CD4细胞数目会随着时间记录下来，处理这种纵向数据强有力的工具是混合模型。近年来，已经提出了各种混合效应模型来研究病毒衰减率。文献［1］提出了具有偏斜度、缺失响应和协变量测量误差的贝叶斯半参数非线性混合效应联合模型；文献［2］提出了带有缺失和测量误差的时变协变量和偏斜正态分布的响应变量的混合效应联合模型；文献［3］提出了具有协变量测量误差的斜正态半参数非线性混合效应模型的贝叶斯推断。Wu［4］提出了同时考虑删失响应和协变量带测量误差的联合模型。已有研究指出，HIV研究中患者间的巨大差异可能与CD4细胞计数有关［5-6］，如图 1所示。从图 1（a）中可以看到在治疗开始后的初始阶段，患者的病毒载量随时间急剧下降。由于研究持续时间较长，病毒轨迹在治疗后期可能会出现反弹，即出现变点，变点的出现可能意味着是更换药物的时候了。此外，病毒载量可能会受检测限（LOD）的限制，当病毒载量低于检测限时会发生左删失［7］。图 1（b）显示了研究中患者的 CD4细胞数目轨迹，可以看到初始阶段大部分CD4细胞数目呈上升趋势，之后轨迹变得复杂。

图1 随机选取的5个HIV病人的病毒载量（a）及CD4细胞数目轨迹（b）Fig.1 Viral load（a）and CD4 cell number locus（b）of 5 randomly selected HIV patients

实际研究中，由于测量计划的不同，CD4细胞数目可能会出现缺失，即得到的CD4细胞数目是离散的。多元线性混合效应（LME）模型［8］要求数据服从正态分布且是连续型变量；广义线性混合模型（Generalized Linear Mixed Models，GLMM）［9—10］中变量可以是离散的，也可以是连续的，而且放宽了变量的分布从而能够解释各种类型的异质性，有助于提高传染病流行病学数据分析的质量。

为了研究重复测量的响应变量和协变量之间的动态关系，已经出现各种推断方法，包括两步法［11］和 Bootstrap 法［12］，Wu［13］考虑了基于泰勒展开的最大似然估计近似方法，Liu和Wu［4］提出了采用蒙特卡罗EM算法实现的似然估计方法。Lunn 等［14］和 Wakefield［15］在非线性混合效应（NLME）模型中引入了贝叶斯方法，贝叶斯方法的优点是可以借鉴类似研究或专家的信息，然后将这些信息以参数的先验分布的形式纳入当前的分析。这些先验信息有助于估计仅通过当前观测数据可能难以识别的参数。

本文针对病毒载量出现测量误差和反弹以及CD4细胞数目离散的情况，将病毒载量作为协变量，CD4细胞计数作为响应变量，联合半参数非线性混合效应模型和广义线性混合模型来模拟HIV动态变化，并用贝叶斯方法估计参数。文章其余部分安排如下：第1节是模型的介绍；第2节是运用WINBUGS软件来实现马尔可夫链蒙特卡罗（MCMC）抽样的贝叶斯方法；第3节通过实例分析，对贝叶斯方法进行了评价，并与朴素贝叶斯方法和两步贝叶斯法进行了比较；第4节对这篇文章进行了讨论。

1 模型

1.1 半参数非线性混合效应模型

假设在HIV治疗中有n个独立个体接受治疗，即n个独立的协变量，xi＝(xi1，…，xini)T表示第i个个体观测到的协变量轨迹，xi含有变点τi，其中xij是第i个个体在时刻tij，i＝1，…，n；j＝1，…，ni的协变量值。在研究期间，并不是所有的τi都能观测到，因为有些个体的轨迹可能在这期间并没有变点出现。因而，个体i观测到的变点是Ti＝min(τi，tini)，记ci＝I(τi≤tini)，其中I(·)为示性函数，即如果τi≤tini，则I(·)＝1；否则I(·)＝0。用zikl表示第i个个体在时刻uil，i＝1，…，n；k＝1，…，v；l＝1，…，mi的响应变量，这里响应变量测量时刻uil不同于协变量测量时刻tij，即允许响应变量里有缺失。用表示，其中zil＝(zi1l，…，zivl)T，l＝1，…，mi。于是观测到的数据可表示为{(xi，zi，Ti，ci)，i＝1，…，n}。

对于协变量，考虑半参数非线性混合效应（SNLME）模型，该模型包含变点和测量误差，具体如下：

其中，X+表示max(X，0)，即变量X和0的最大值，g1(·)，g2(·)和d(·)是已知的参数函数，ω(t)和hi(t)分别是未知的非参数固定效应和随机效应平滑函数。是个体i和时间有关的函数，β*是总体参数，eij是随机误差，是随机效应。记ei＝(ei1，…，eini)T，假设：ei～i.i.d.N(0，δ2I)，，其中B*是无结构方差协方差矩阵，hi(t)，s是一个零均值随机过程的独立同分布实现。为简便起见，设bi，hi(t)与ei独立。

非参数函数ω(t)和hi(t)可用基函数Ψp(t)＝(ψ0(t)，…，ψp—1(t))和Φq(t)＝(ϕ0(t)，…，ϕq—1(t))的线性组合来近似，具体如下［16］：

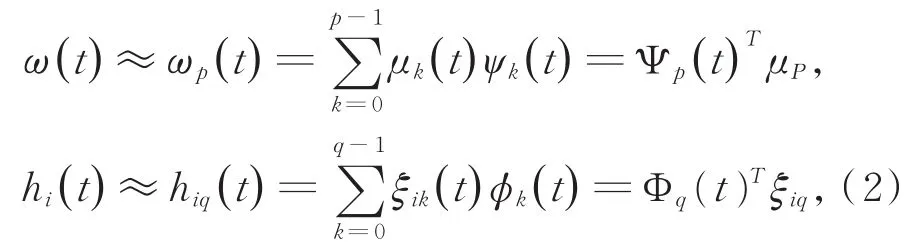
其中：μp和ξiq分别是未知的固定效应向量和随机系数，ξiq是一个零均值随机向量的独立同分布实现。考虑基于百分位数结点的三次样条自然基函数，由AIC或BIC准则来确定结点的个数。如果ω(t)和hi(t)用它们的近似ωp(t)和hiq(t)来代替，则SNLME模型（1）可用下面的参数NLME模型来近似：

其中，β＝(β*，μp)为固定效应，是随机效应，bi～i.i.d.N(0，B)，其中B是无结构方差协方差矩阵，g(·)是已知的参数函数。

1.2 广义线性混合模型

广义线性混合模型（GLMM）是在广义线性模型的基础上将随机效应引入均值方程中来处理重复测量之间的相关性，其构成与广义线性模型相似，也是由随机成分、系统成分和连接函数三部分构成。随机成分假设因变量服从指数分布族；系统成分为线性预测部分，随机效应体现其中；连接函数为连接系统成分和随机成分的函数，一般采用对数连接。对于离散的纵向数据，本文采用广义线性混合模型（GLMM）进行建模：

定义zil＝(zi1，…，zimi)T为个体i在时刻uil(i＝1，…，n；l＝1，…，mi)观测到的响应变量的值，其均值为响应变量的线性函数。这里假设重复测量值zi1，…，zimi服从指数族的分布，即zi的概率密度函数可以表示如下：

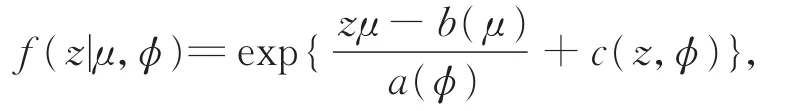
其中，a(·)，b(·)，c(·)是特定函数，μ为均值，ϕ为方差，则：

广义线性混合模型（GLMM）如下：

其中，ωij＝E(zij|α，ai)为条件均值，g(·)为连结函数，xij为病毒载量，α为固定效应，ai为随机效应，可以反应不同观测对象之间的异质性以及对同一观测对象的多次观测之间的相关性，A为协方差矩阵。这里假设随机效应ai与zi1，…，zimi相互独立。

1.3 变点模型

协变量轨迹发生变化的时刻τi和响应变量及协变量有关。假定τi条件依赖于响应变量模型（4）中的ai及协变量模型（3）中的随机效应bi，τi～f(t|ai，bi，γ，η)，其中γ和η是未知参数。考虑如下模型：

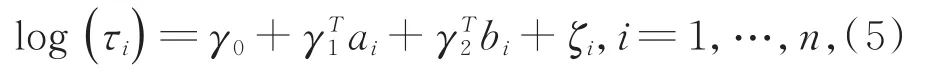
2 参数估计的贝叶斯推断

2.1 联合贝叶斯推断方法

在纵向数据研究中，响应变量和协变量通常在物理学上或生物学上相关。尽管对响应变量和协变量的联合似然函数进行推断有利于参数估计，但联合似然推断的计算量巨大且会导致收敛性问题。为解决该问题，本文针对模型（3），（4）和（5），基于MCMC算法提出联合贝叶斯推断方法。

设D＝{(xi，zi，Ti，ci)，i＝1，…，n}表示观测数据，θ＝(α，β，γ，δ，A，B，η)表示所有未知模型参数的集合，f(·|·)和π(·)分别表示条件密度函数和先验密度函数。假定α，β，γ，δ，A，B，η相互独立，即π(θ)＝π(α)π(β)π(γ)π(δ)π(A)π(B)π(η)。为进行贝叶斯推断，需要给出模型（3），（4）和（5）中未知参数的先验分布。设均值参数α，β，γ服从正态先验分布，而精度参数δ，η，A，B服从伽马分布（Gamma）和威沙特分布（Wishart）：

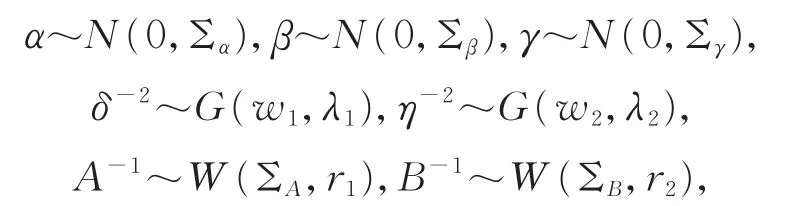
其中：超参数w1，w2，r1，r2，Σα，Σβ，ΣA，ΣB和Σγ已知，伽马分布G(w，λ)和威沙特分布W(v，Σ)均值分别为wλ和vΣ。实际应用中，可以从已有的研究或参考文献中获得先验信息。对有可靠先验信息的参数，可以使用具有小的方差的强先验，对没有足够先验信息的参数，可以使用弱先验（具有大的方差）。而且，进行灵敏度分析时，对参数可以尝试不同的先验分布或不同的参数值。

当模型及其参数的先验分布确定后，在贝叶斯框架下可基于参数的后验分布对参数进行统计推断。未知参数θ的联合后验密度由下式给出：

一般地，（6）式中的积分都是高维积分且没有解析解，而对解析解进行近似可能不够准确。因此，基于观测数据直接计算的后验分布不可行。作为代替，可用MCMC方法基于（6）式使用Gibbs抽样器和Metropolis-Hasting（MH）算法进行抽样。

2.2 算法的具体实现

为了避免计算（6）式的积分，从后验分布中进行采样，本文引入潜在变量(a，b)≡{(ai，bi)，i＝1，…，n}。为了运行Gibbs抽样，需要条件分布：令α—1表示θ中除α以外的其他参数，同样定义β—1，γ—1，δ—1，η—1，A—1和B—1，

精度参数的满条件分布为：

贝叶斯推理可以基于Gibbs抽样和M—H算法，利用Gibbs抽样从后验分布中生成样本的描述如下。在第t次迭代时：

（6）精度参数δ—2，A—1，B—1，η—2由它们的全条件分布可得。

在上面的Gibbs方法中，采用M—H算法更新。从初始值开始，过一段时间后，从后验分布收集MCMC样本。然后，根据后验均值或分位数对未知参数进行统计推断。

3 实例分析

3.1 模型实现

该研究包含46名HIV感染患者，他们在研究开始时接受了抗HIV治疗。在开始治疗后第0，2，7，10，14，21，28天和第 8，12，24，48周测量病毒载量，在整个研究中也记录了CD4细胞数目，每位患者的观察次数从4到10次不等。

为了避免观察值之间的差异过大，对病毒载量的原始值进行以10为底的对数变换。图2显示了研究中包含变点的所有患者的病毒载量轨迹，可以看到部分病毒载量低于检测限（log10(100)＝2），即存在左删失，对于低于检测限的病毒载量统一替换为log10(50)＝1.69。由于测量时间的不同，在病毒载量的测量时间tijCD4部分缺失。因此，参照Little和 Rubin［17］，这里假设 CD4 的缺失是随机的，即缺失的数据机制是可忽略的。为了避免过小（过大）估计，将CD4的值进行标准化（减均值除以标准偏差）并重新调整原始时间t（以天为单位），使其取值介于0和1之间。

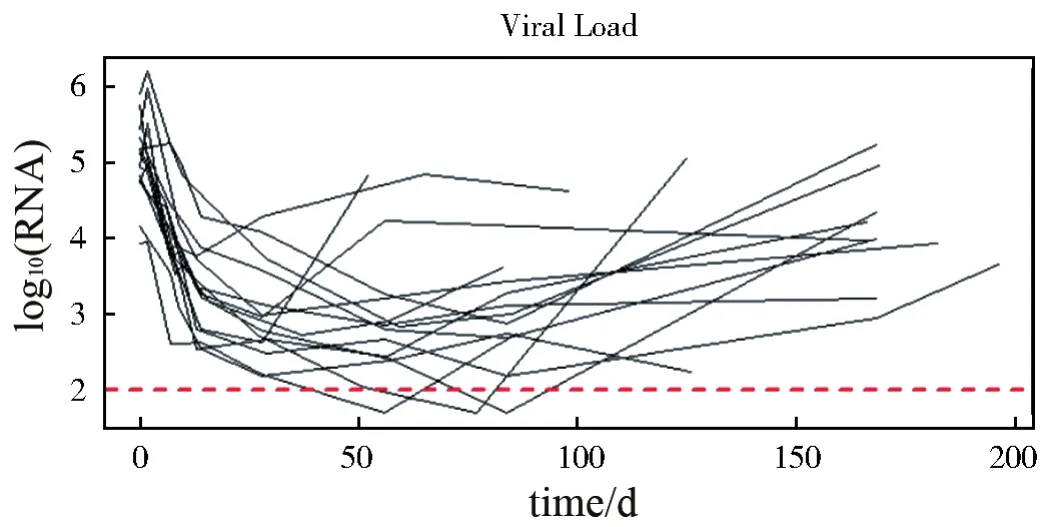
图2 研究中包含变点的所有患者的病毒载量轨迹Fig.2 Viral load trajectories of all patients that include change point in the study

另外，为判断个体病毒载量是否存在变点，建立以下标准：

1.在达到最小病毒载量后至少有两个观察值；

2.在最小病毒载量后有一个观察值，但是反弹之后斜率的绝对值大于最小观察值之前的斜率的绝对值。

如果满足上述两个标准中的任何一个，就认为轨迹中存在变点。

由于一些患者的病毒载量轨迹具有变点，故很难建立参数模型来拟合变点之后的部分。对此，使用非参数模型，结合一些基本样条函数来拟合它。即对长期病毒载量数据使用以下双指数SNLME模型：

其中，xij表示第i个病人在时间tij的病毒载量的对数化值，P1i和P2i是tij＝0时的基准值，λ1ij和λ2ij分别表示第一、二阶段病毒的衰减速度。τi是第i个病人的变点位置，eij表示随机误差，bki是随机效应（表示个体与总体均值的差异）。ω(tij)和hi(tij)分别是非参数固定效应和随机光滑函数。假设β1＞β3和β2＞0［18］。

采用AIC或BIC准则进行模型选择。由于潜在的随机效应数量众多，首先基于AIC和BIC准则确定变点之前的模型（参数NLME模型）。此外，本文通过基本样条函数的线性组合来逼近非参数函数si(tij)。令ϕ0(t)≡ψ0(t)≡1，取与（2）式中相同的三次样条函数，其中q≤p。由AIC/BIC准则可确定模型（2）中p＝3，q＝1（503.1167/573.1165）即：

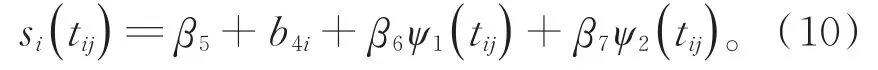
对于响应变量CD4，由于缺乏基于生物的数学模型，往往是经验建模。一种流行的方法是将计数在200阈值处一分为二，因为此阈值是人类免疫系统的一个重要阶段［19］。本文采用200作为截止点，如果患者i在j时刻CD4计数大于200，则为"zij＝1"，否则"zij＝0"。采用AIC/BIC准则进行模型选择，使AIC/BIC达到最小值（288.04/322.47）的模型如下：

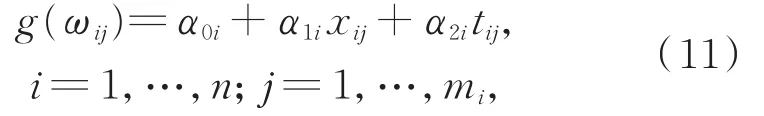
其中，ωij＝(E[CD4ij|α，ai])，，α＝(α0i，α1i，α2i)T和ai＝(a0i，a1i，a2i)T分别为固定效应和随机效应，且ai～N(0，A)，α0i＝α0+a0i，α1i＝α1+a1i，α2i＝α2+a2i。

通常可使用随机效应建模的方法来模拟变点的位置，本文对变点采用如下模型［20］：

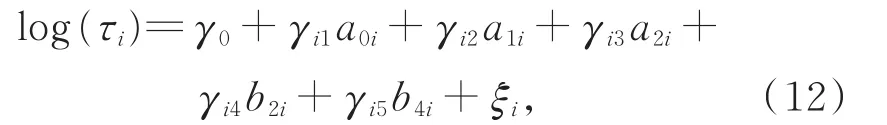
其中，ξii.i.d～N(0，η2)。

3.2 结果分析

本节中，使用了三种方法来估计模型参数并对其结果进行比较。为减少对先验信息的依赖，假定所有参数都服从弱先验分布。具体地，（i）设固定效应服从正态分布N(0；100)并和总体参数向量α，β，γ独立；（ii）尺度参数η2和δ2服从无信息的逆伽马分布，IG(0.01；0.01)，该分布均值为1，方差为100；（iii）方差协方差矩阵A，B的先验分布可取为逆威沙特（Inverse Wishart）分布IM(Ω1，v1)和IM(Ω2，v2)，其中自由度v1＝3，v2＝4，Ω1和Ω2是主对角元素为1的对角矩阵。

利用WinBUGS［21］来实现MCMC抽样，通过如下两步迭代实现：（i）利用Gibbs抽样更新α，β，γ，η，σ，δ，A，B；（ii）用M—H方法更新ai和bi，i＝1，2，…，n。采集最终的MCMC样本对未知参数做统计推断，给出后验均值和置信区间。当MCMC程序用于实际临床数据时，可使用WinBUGS中的标准工具（例如跟踪图）评估生成样本的收敛性。样本收敛后，去掉初始的50 000次迭代，在接下来的100 000次迭代中每20个MCMC抽样中选取一个，这样就得到了5 000个用于统计推断的未知参数后验分布的样本。

表1和表2给出了基于联合贝叶斯方法（JBA）、两步贝叶斯方法（TSBA）和朴素贝叶斯方法（NBA）的部分模型参数的总体后验均值（PM），对应的标准差（SD）和95%置信区间（LCI表示置信下限，UCI表示置信上限）。在联合模型中，估计结果显示大部分的估计具有统计学显著性（因为95%置信区间不包含0），而且两个联合模型方法（JBA和TSBA）给出了类似的参数估计结果。对于响应变量的参数估计，可以得出两种联合模型方法（JBA和TSBA）没有太大差异。但是TSBA相比于JBA方法有更小的标准偏差，这主要是由TSBA方法忽略了响应变量的真值和其估计值之间的差异导致的。此外，JBA方法中，α1的后验均值小于0，说明开始治疗后，病毒载量减少，CD4细胞数目会增加，符合图1中所描述的轨迹。对于协变量的参数估计，JBA方法中第一阶段递减率β2＝60.26＞0且远远大于β4，说明SNLME模型的参数估计值是合理的。对于尺度参数，估计结果显示：与TSBA法比较，JBA方法的估计结果均值更接近0，基本符合随机误差项的正态性假设。

表1 JBA、TSBA和NBA三种方法的部分参数后验估计Table1 Posterior estimation of partial parameters of JBA、TSBA and NBA

表2 变点模型中部分参数的后验估计及尺度参数估计Table 2 Posterior estimation and scale parameter estimation of some parameters in change point model

图3给出了六个随机选择的病人的基于三种估计方法的病毒载量轨迹的拟合曲线。六个病人中三个存在变点，三个无变点。实线、虚线和点线分别表示TSBA、NBA和JBA方法的拟合轨迹。从图3可以看出，JBA和TSBA方法给出了类似的病毒载荷拟合轨迹，两种方法均优于NBA方法。原因是NBA方法忽视了响应变量中的测量误差。当病人的轨迹含有变点时，NBA方法的效果更差，因为它没考虑病毒载量的反弹。

图3 随机选择病人的JBA方法、TSBA方法和NBA方法的病毒载量拟合曲线Fig.3 Viral load fitting curves of JBA，TSBA and NBA methods for randomly selected patients

为评估GLMM的拟合效果，图4分别给出了标准化残差散点图和拟合概率曲线图。从图4（a）可以看出，所描绘的大部分点比较均匀地落在（—2，2）的水平带状区域中；从图 4（b）可以看出拟合概率曲线基本满足logistic模型的S型曲线，说明GLMM拟合响应变量模型效果较好。

图4 标准化残差散点图（a）和拟合概率曲线图（b）Fig.4 Scatter plot of standardized residuals（a）and fitting probability curve（b）

4 结论

本文针对病毒载量有测量误差和反弹以及CD4细胞数目离散的性质，联合非线性混合效应（NLME）模型和广义线性混合模型（GLMM），提出了含有变点的半参数非线性混合效应（SNLME）联合模型，并在贝叶斯框架下估计参数。该模型能很好地拟合长期轨迹特别是病毒载量存在变点的轨迹，实例分析表明本文提出的联合贝叶斯法（JBA）优于朴素贝叶斯（NBA）和两步贝叶斯法（TSBA），能给出更可靠的参数估计。

分析结果表明第一阶段病毒衰减和CD4的数值存在显著的正相关关系，由于病毒衰减率反映了抗逆转录病毒治疗的效果，高的CD4值可能需要较低的药效来抑制病毒复制，而CD4数值的快速下降可能和早期反弹相关。这些发现可能有助于提高对HIV感染发病机制的理解和抗逆转录病毒治疗的评估。目前已研制出单克隆抗体药物Ibalizumab［22］治疗艾滋病，但只有早发现、早治疗才能为病人选择最佳治疗时机。

此外本文在数学建模和统计推断上借助MCMC方法得到参数估计值，该方法可以处理数据量较少的情况，而且算法收敛性好，大大减轻了似然估计会遇到的庞大的计算负担。HIV/AIDS复杂性会带来一些挑战，例如不可忽视的缺失数据，仪器测量的精度问题、模型误差假设问题。针对这些问题，可以在本文研究的基础上，作为下一步的研究方向。