带有时滞与动力学边界条件的波方程解的爆破

郝江浩，霍秋宇

（山西大学 数学科学学院，山西 太原 030006）

0 引言

本文研究如下带有时滞与动力学边界条件的波方程的初边值问题，

其中u＝u(x，t)，Ω是RN(N≥1)中的有界区域，∂Ω＝Γ0∪Γ1，meas(Γ0)＞0，，且表示外法向导数，p＞2，m≥2.常数τ＞0是时滞，α，μ和r是常数，，u1∈L2(Ω)，f0∈L2(Ω×(0，τ))是已知函数。

方程（1）可以看作是描述弹性介质与刚性质量相互作用的模型。这个模型在实际应用中非常常见，研究这类模型的相关文献也比较多，参见文献［1-2］。Ball［3］研究了带有源项的波方程utt—Δu＝|u|γ—1u，利用凸性方法证明了源项导致带有负的初始能量的解在有限时刻爆破。Gerbi和Said-Houari［4］考虑了带有动力学边界条件的半线性阻尼波方程的渐近行为，利用势阱方法证明了当初值在稳定集中解是渐近稳定的，基于文献［5］的凸性方法证明了当初值在不稳定集中解在有限时刻爆破。Messaoudi［6］研究了带有狄利克雷边界条件的非线性黏弹性波方程，给出了带有任意负的初始能量的弱解在有限时间内爆破。我们都知道时滞是系统不稳定的一个来源，甚至任意小的时滞可以使一个稳定的系统变得不稳定。Kafini和Messaoudi［7］研究了带有狄利克雷边界条件与时滞的非线性波方程，在时滞项、阻尼项以及源项满足合适的条件下，解在有限时间爆破，关于此类方程解的爆破问题可参看文献［8-11］。

从上面的文献来看，带有动力学边界条件与时滞的波方程研究的并不多。本文利用文献［6-7，12］等的方法得出了初边值问题（1）的解在有限时间爆破的结果。文章结构如下，在第1节给出一些假设、准备工作和主要结论。在第2节给出方程（1）主要结论的证明。

1 准备工作和主要结论

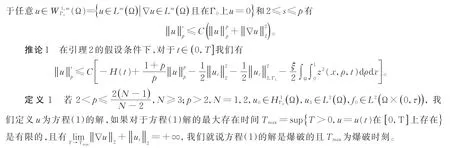
2 主要结论的证明