含裂纹损伤圆弧曲梁弹性屈曲的有限元网格自适应分析

王永亮

(1. 中国矿业大学(北京)力学与建筑工程学院，北京 100083；2. 中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083)

杆系结构的损伤问题广泛存在于工程实际中，工程杆系结构大多带裂纹工作[1-2]，裂纹损伤的存在会改变整个结构的力学性能，影响结构的安全性和适用性[3]。研究含多裂纹损伤梁构件的动力特性、准确预测屈曲承载力可以有效地保障结构在全生命周期内安全使用[4]。曲线形梁构件由于几何形态复杂，容易诱发弹性屈曲失稳[5]，精确评估各类曲线梁线型、不同曲梁夹角下深梁、浅梁的屈曲荷载成为结构灾害分析的重要依据。曲梁中裂纹损伤的存在增加准确预测屈曲失稳承载能力的难度，理论模型、解析方法等往往难以有效分析[6-7]。准确预测不同裂纹损伤位置、大小、数目工况下屈曲荷载承载力以及分析裂纹损伤对屈曲失稳的影响机理[8]，成为理论研究和工程实践的需求。

有限元法被发展和应用于求解含裂纹损伤曲梁的弹性屈曲荷载和屈曲模态[9-11]，但解答精度依赖于网格划分质量，解答因网格划分难免引入误差[12]。有限元网格自适应分析方法可有效地优化网格分布，在直线梁弹性屈曲[13]、板壳振动[14]、含损伤梁振动[15]、岩体变形和断裂[16]等问题求解中展示出很好的求解效力。本文将建立圆弧形曲梁裂纹的截面损伤缺陷比拟方案，进行裂纹大小(深度)、位置、数目的模拟，引入变截面Euler-Bernoulli梁的h型有限元网格自适应分析方法[15]，求解含裂纹损伤圆弧曲梁弹性屈曲问题，得到优化的网格和满足预设误差限的高精度屈曲荷载和屈曲模态。文中给出求解多种圆弧曲梁弹性屈曲数值算例，对网格自适应划分以及弹性屈曲解答的收敛性进行了讨论，对曲梁夹角、损伤位置、数目、大小等因素影响弹性屈曲荷载和屈曲模态进行了分析，检验了网格自适应划分的有效性。

1 圆弧曲梁弹性屈曲

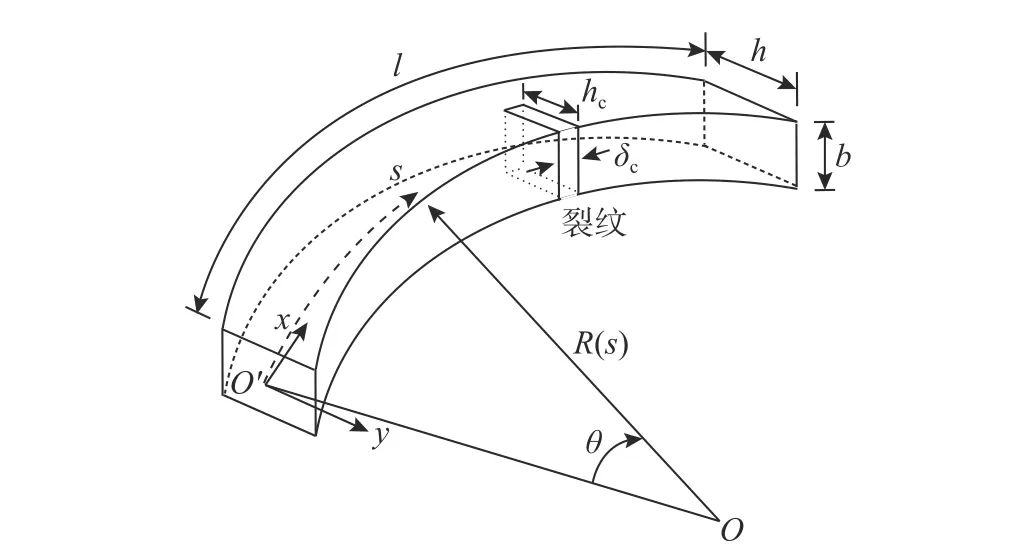
图 1 含裂纹损伤曲梁坐标系和符号Fig. 1 Coordinate systems and symbols of cracked curved beam

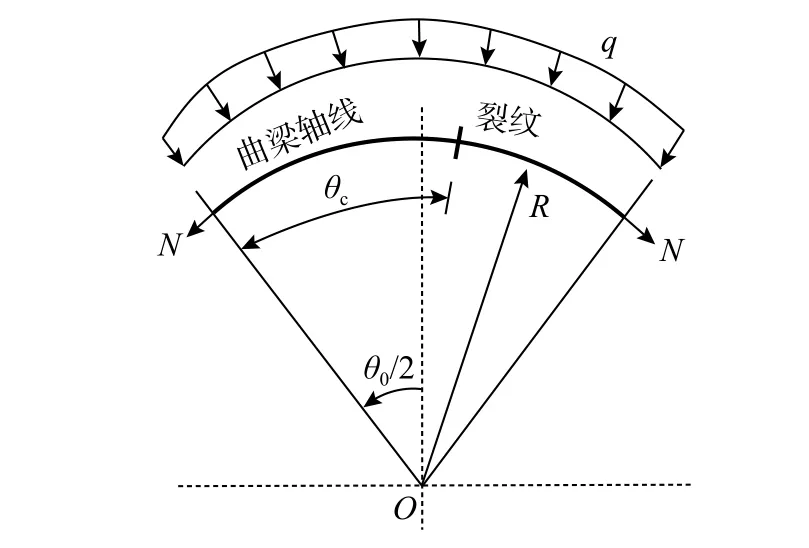
图 2 含裂纹损伤圆弧曲梁截面损伤和加载示意图Fig. 2 Diagram of cross-section damage defect and loading for circularly curved beam with crack damage

表 1 圆弧曲梁根据径厚比和夹角分类Table 1 Categories of circularly curved beams according to ratio of radius and thickness and subtended angle

本文研究圆弧曲梁弹性屈曲的微分控制方程为[13]：

2 裂纹损伤表征方法

本文采用Euler-Bernoulli梁理论模型研究梁高相对较小薄曲梁，若裂纹损伤发生在梁单一侧，则损伤截面中性轴与无损伤截面偏移量较小；若裂纹损伤均匀发生在梁上下两侧，则损伤截面中性轴与无损伤截面完全重合。因此，本文研究的曲梁无裂纹和有裂纹横截面仅高度不同，二者中性轴考虑为处于相同位置。曲梁中的裂纹损伤，使得梁截面产生弱化、梁的抗弯刚度衰减。本研究采用裂纹的截面损伤缺陷比拟方法[15]，裂纹处的截面刚度为：

3 网格自适应细分加密

有限元计算存在相比当前网格解答具有更高收敛阶的超收敛点[19]，利用超收敛点结合单元拼片、高阶形函数插值技术，可以提高当前有限元解的精度，得到全域的超收敛解[15,20-21]。本文对于圆弧曲梁的弹性屈曲问题，求得当前网格下屈曲模态(位移)的有限元解后，利用有限元后处理超收敛拼片恢复方法，得到屈曲模态的超收敛解：

利用屈曲模态误差估计，网格可以进行优化处理来降低和控制屈曲模态的误差，达到预设的解答精度。本文方法对每个有限元单元e上的振型误差进行判断，如果误差控制式(12)不满足，则表明该单元上屈曲模态解答的误差过大，需要通过进行网格优化处理，本文采用单元均匀细分加密的h型网格自适应方式来增加模型自由度、降低单元上解答的误差[15]。当前单元细分生成的新单元长度与目前误差和单元阶次相关，即利用当前误差可以估计新单元长度：

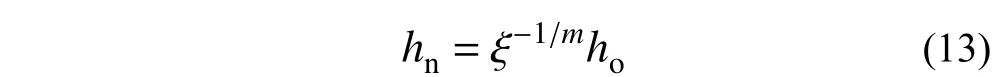
4 数值算例

本文方法已经编制相应的Fortran 90语言程序代码，程序开发实施基于Microsoft Visual Studio和Intel Visual Fortran编程软件平台。本节给出求解具有代表性的多种圆弧曲梁弹性屈曲数值算例，对网格自适应划分以及弹性屈曲解答的收敛性进行了讨论，对曲梁夹角、损伤位置、数目、大小等因素影响弹性屈曲荷载和屈曲模态进行了分析，检验了网格自适应划分的有效性。本节所有算例均采用3次元，初始网格采用2个单元，给定的初始误差限为。

4.1 圆弧曲梁屈曲分析的网格优化

考虑一两端简支的圆弧曲梁，梁的几何和物理参数如下：

本文方法对该曲梁弹性屈曲进行求解，得到屈曲荷载和屈曲模态的解答。文献[23]采用层状组合梁模型及有限元方法、文献[7]采用理论模型解析法分别对该梁弹性屈曲进行分析，得到无裂纹损伤梁屈曲荷载值。为进行对比分析，将上述各方法求得的屈曲荷载值均列于表2。同时，为讨论网格数目对解答收敛的影响，本研究采用常规有限元法在4个、5个、6个单元(稀疏均匀网格)以及25个、50个、100个单元(密集均匀网格)上分别进行求解，得到屈曲荷载值；可知随着单元增多，解答趋于稳定，在接近100个单元时得到收敛解答。使用本文自适应有限元方法进行求解，得到仅为16个单元的优化网格和在此网格下的收敛解答，该屈曲荷载解答(64.406 kN/m)与理论模型解析解(64.966 kN/m)具有很好的吻合度。需要说明的是，组合梁模型使用4个、5个、6个单元得到的解答与解析解相差较大，为梁模型的层状建模引起。

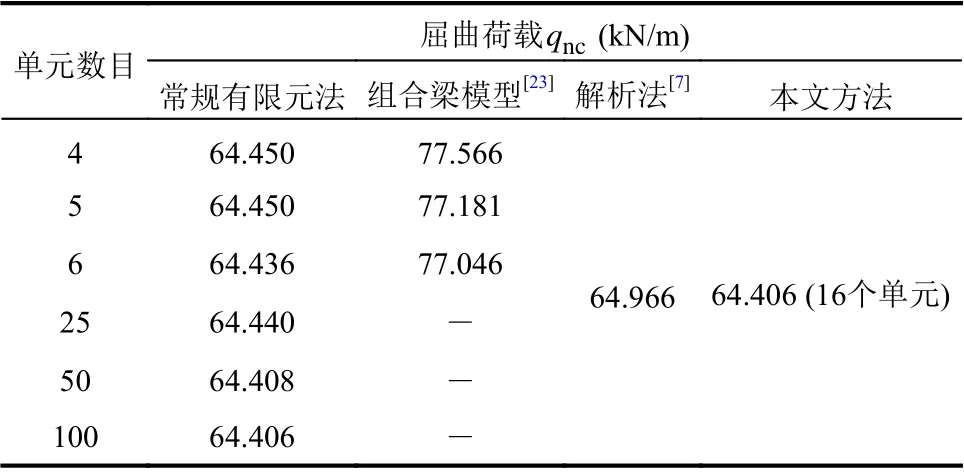
表 2 单元数目与屈曲荷载结果收敛性Table 2 Convergence for number of elements and buckling loads results

图3给出本文方法利用自适应网格求解得到的屈曲模态解答，为方便直观显示和分析，屈曲模态结果均进行归一化处理(令最大模态值为1)。由于该梁的物理性质和几何形态具有左右对称性，得到图3(a)所示的屈曲模态亦为左右对称形式；同时，水平坐标轴上给出了本文的自适应网格(单元端节点)分布，可知单元分布适应模态变化、同样具有左右对称性，且在两端边界部分使用了相对细密的网格。算法自动优化出非均匀网格，在屈曲模态变化平缓区域使用稀疏网格、在屈曲模态变化剧烈处采用了相对细密的网格，避免了全域使用一致细密网格的冗余性。为了检验屈曲模态解答的精确性，本研究使用常规有限元法2500个单元(高密集均匀网格)求解得到高精度屈曲模态作为解析解；该高精度屈曲模态形态与图3(a)相同，这里不再给出。图3(b)所示为使用本文自适应方法的屈曲模态与高精度屈曲模态的差值曲线分布，该差值曲线最大值2.17×10-5小于预设误差限10-4，验证了本文方法求解解答的精确性。

常规有限元采用4个、5个、6个、25个、50个、100个单元求解得到的屈曲模态解答与高精度屈曲模态解答的差值分布分别如图4所示，并在图中水平坐标轴上给出各网格分布。各单元下差值在全域上的最大值分别为1.23×10-1、1.23×10-1、4.12×10-3、7.70×10-3、1.62×10-3、2.63×10-6，可见随着网格的均匀加密，屈曲模态解答的误差呈现逐渐降低的趋势；直到提供足够多的单元(100个单元)时，才接近获得满足预设误差限10-4的解答。本文自适应方法仅采用16个单元的非均匀分布网格，即可避免高密度均匀分布网格的单元冗余性，提高了计算效率。

图 3 自适应网格下屈曲模态Fig. 3 Buckling mode on adaptive refinement mesh

4.2 变曲梁夹角下的屈曲荷载

为检验本文方法求解不同几何形式圆弧曲梁弹性屈曲的适用性，本研究对不同圆弧夹角曲梁(浅梁、深度梁)进行分析。考虑一两端简支的圆弧曲梁，梁的几何和物理参数如下：

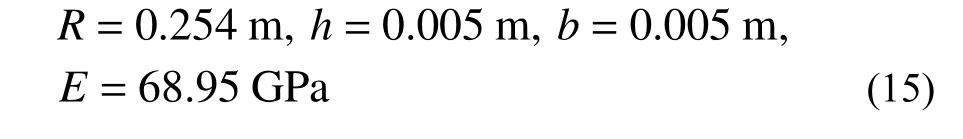
4.3 弹性屈曲的裂纹损伤位置影响

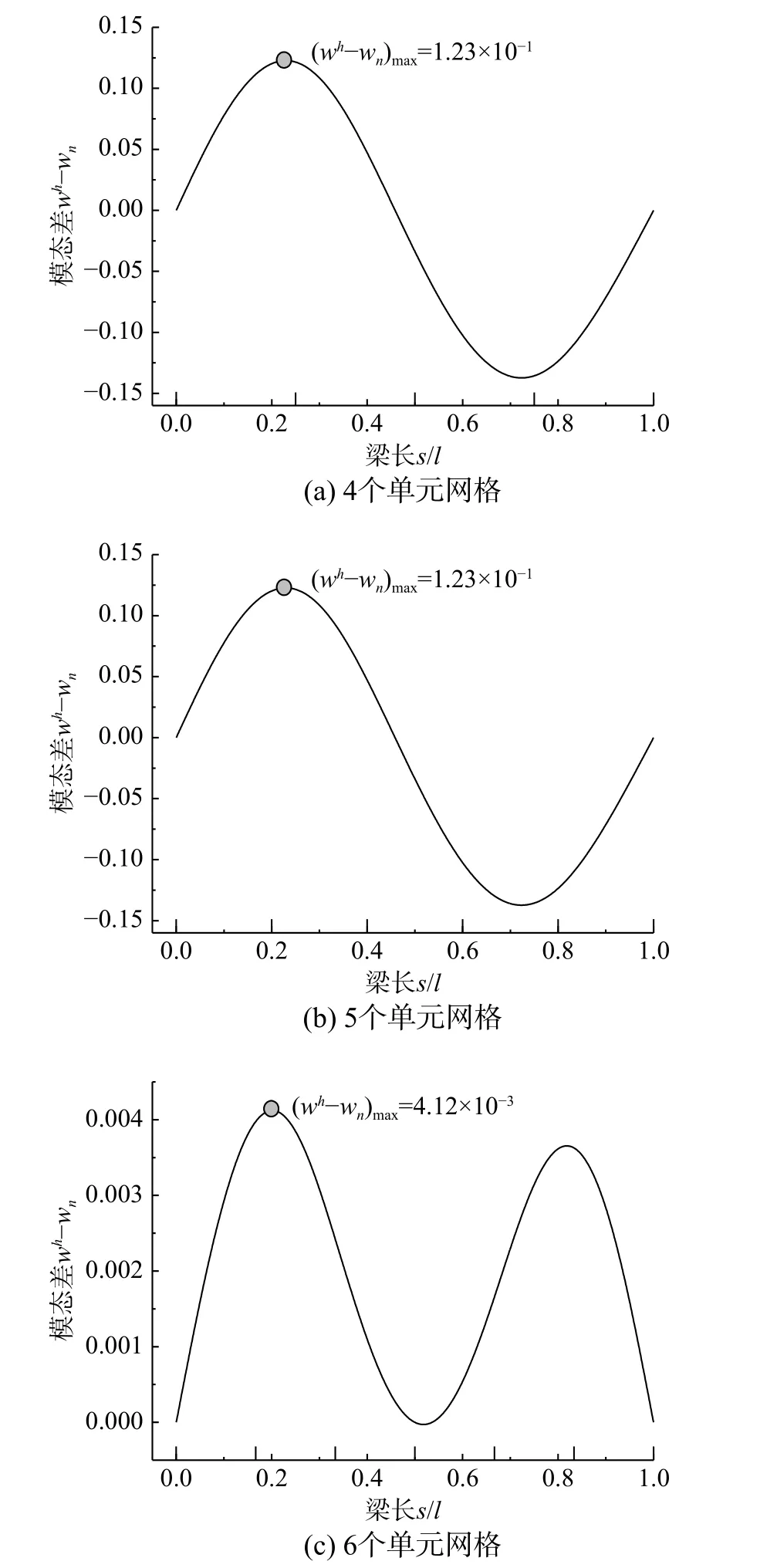
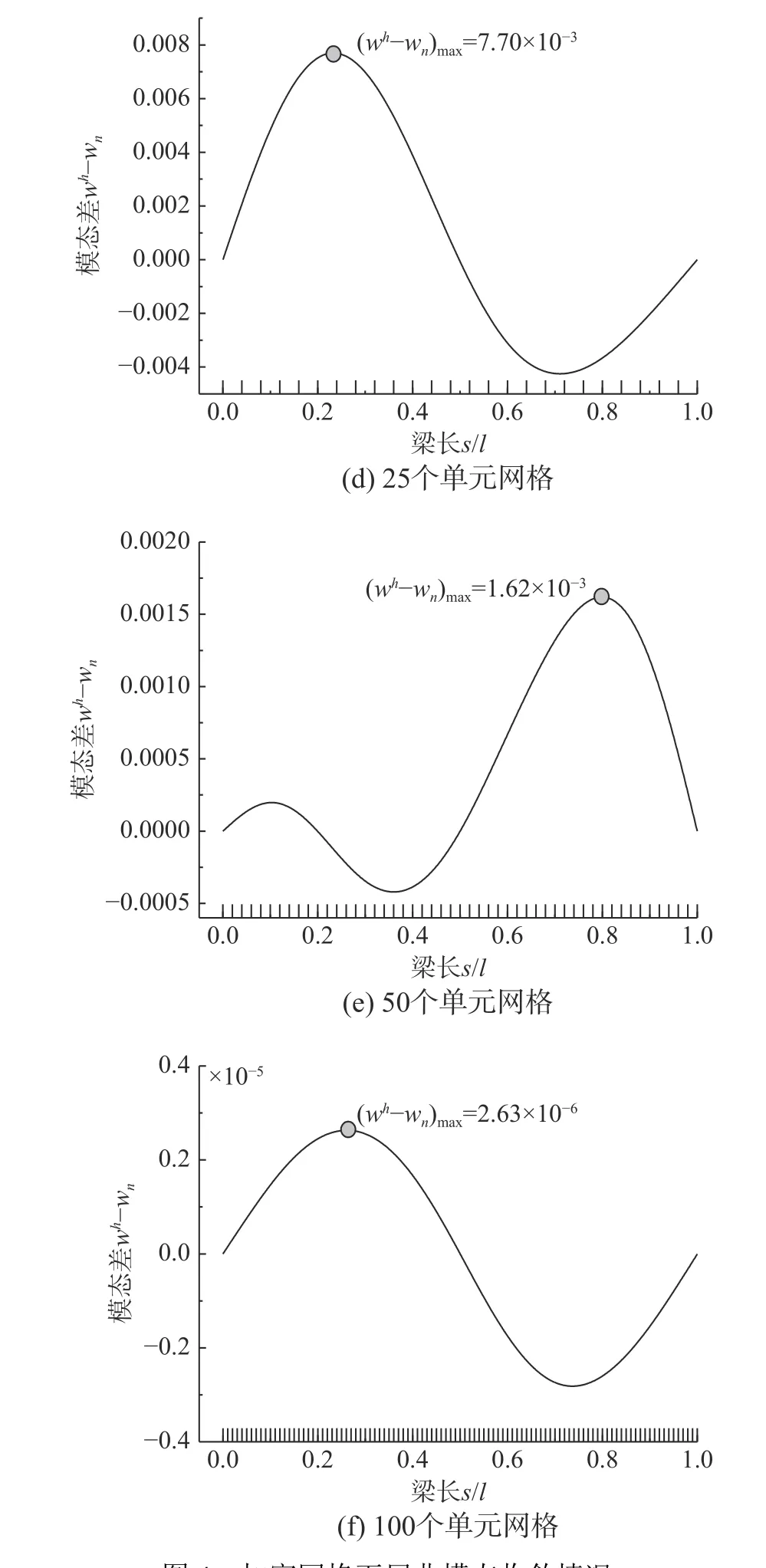
图 4 加密网格下屈曲模态收敛情况Fig. 4 Convergence of buckling modes on refined meshes

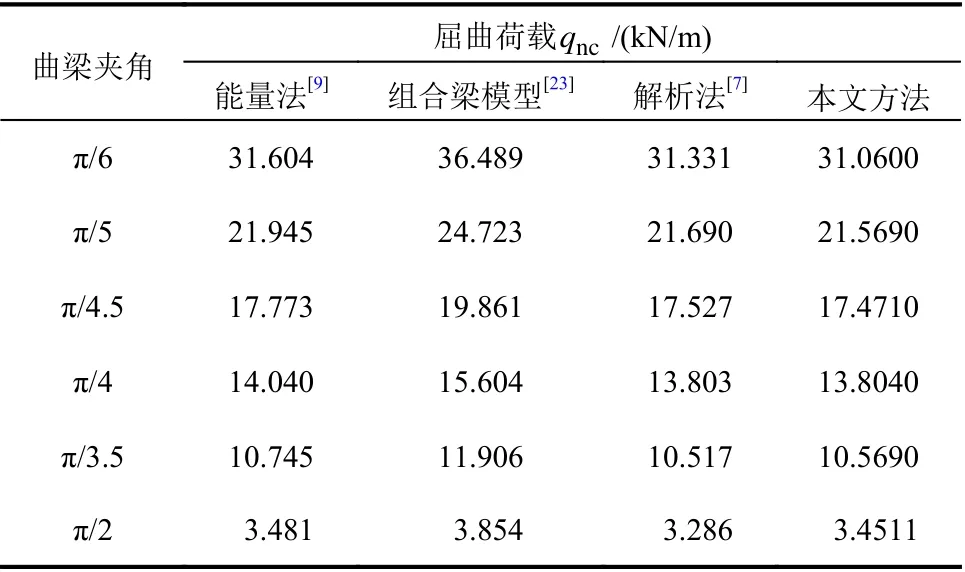
表 3 两端简支曲梁不同夹角下屈曲荷载值Table 3 Buckling loads of of curved beam with hinged-hinged supports under different subtended angles

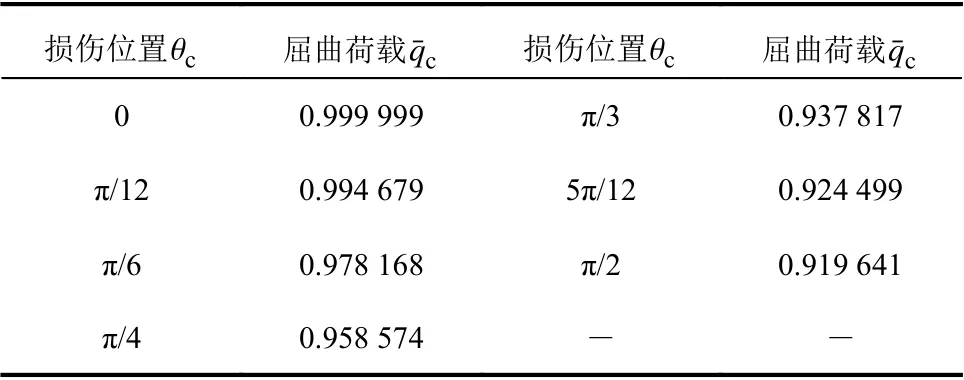
表 4 不同裂纹损伤位置下曲梁屈曲荷载值Table 4 Buckling loads of curved beam with crack damage at different locations

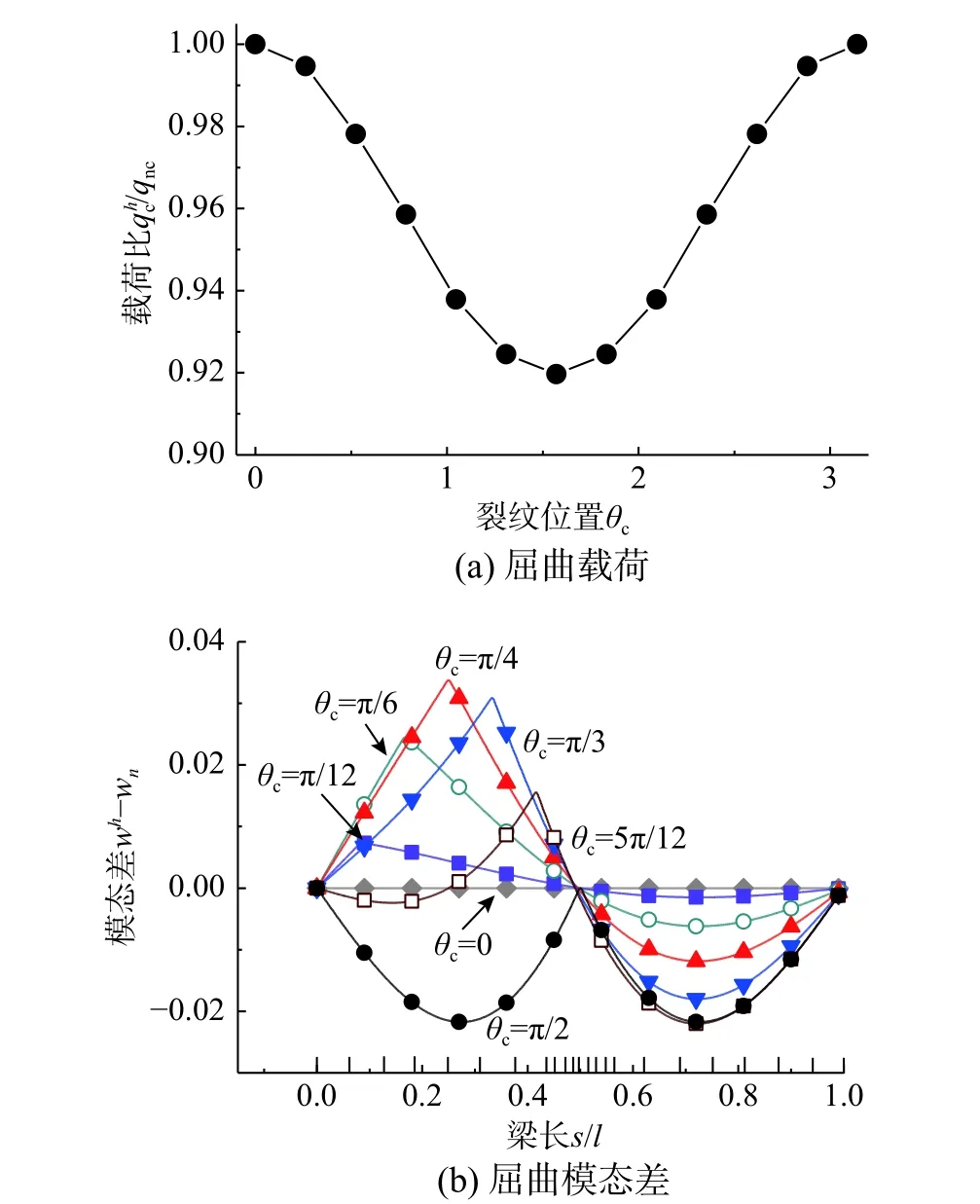
图 5 不同裂纹损伤位置下圆弧曲梁弹性屈曲Fig. 5 Elastic buckling of circularly curved beam with different locations of crack damage

4.4 弹性屈曲的裂纹损伤大小影响

本节分析圆弧曲梁裂纹损伤大小(深度)对弹性屈曲的影响，固定裂纹损伤位于跨中(θc=π/2)，分析裂纹损伤大小hc/h值为0.1、0.2、0.3、0.4、0.5时的弹性屈曲。使用本文方法分别进行求解，得到弹性屈曲荷载解答，结果列于表5。可知，随着裂纹损伤hc增大(hc/h=0.1 →0.5 )，q¯c逐渐降低。

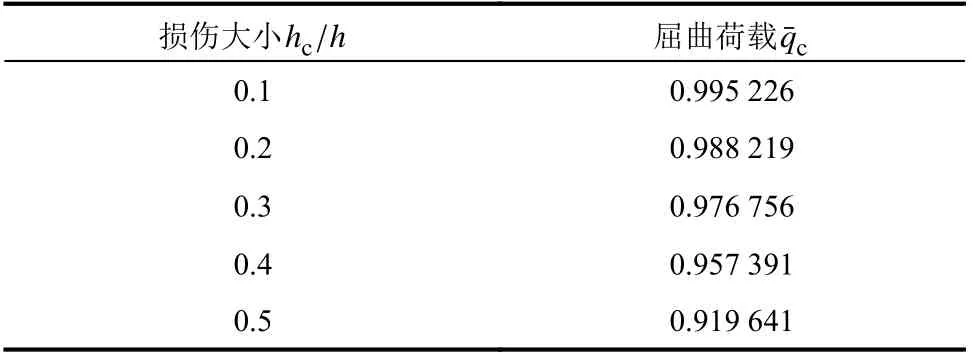
表5 不同裂纹损伤大小下曲梁屈曲荷载值Table5 Buckling loadsof curved beam with crack under different magnitudes

为更直观显示和分析变化趋势，利用上述不同裂纹损伤大小下屈曲荷载结果绘制图6(a)所示变化曲线。可见屈曲荷载随裂纹损伤加深，出现准线性的降低趋势；在裂纹扩展到梁高的一半(hc/h=0.5)时，屈曲荷载承载力降低约10%。图6(b)所示为不同裂纹损伤大小时各屈曲模态与无损伤屈曲模态的差值曲线，可以看出裂纹损伤大小对屈曲模态变化幅度具有重要影响，裂纹损伤程度越大，越容易诱发屈曲模态的大幅度变化。同时，水平坐标轴上给出本文方法求解hc/h=0.5时的自适应最终非均匀网格。

4.5 多裂纹损伤下屈曲模态和网格划分

为分析多裂纹损伤对曲梁弹性屈曲的影响，采用图7 所示的两端简支圆弧曲梁，该曲梁夹角为θ=π，其余基本几何和物理参数同式(12)。该曲梁包含3条裂纹损伤，考虑I(裂纹损伤沿曲梁均匀分布)、II(裂纹损伤集中于曲梁端部)、III(裂纹损伤集中于曲梁中部)等3种工况，各工况中裂纹分布角坐标值如表6所示，裂纹分布如图7所示。

使用本文方法计算该曲梁多裂纹工况的结果如表6所示，工况III的屈曲荷载值最小，即多裂纹损伤越集中于跨中，越容易诱发弹性失稳，这与上文单一裂纹损伤位于跨中易于导致弹性失稳的结论一致。

图8所示为多裂纹工况各屈曲模态与无损伤屈曲模态的差值曲线，可以看出各裂纹损伤所在局部区域对屈曲模态变化有重要影响，多裂纹损伤缺陷导致屈曲模态剧烈变化。同时，本文算法在各裂纹损伤附近区域使用了相对密集的网格，用于适应裂纹损伤引起屈曲模态的变化，形成优化的非均匀网格、确保解答的可靠性。

表6 多裂纹损伤不同位置下曲梁屈曲荷载值Table 6 Buckling loadsof curved beam with multiple cracks at different locations

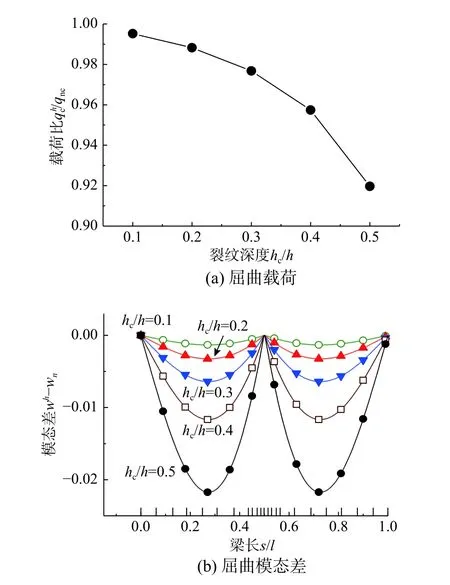
图6 不同裂纹损伤大小下圆弧曲梁弹性屈曲Fig.6 Elastic buckling of circularly curved beam with different magnitudes of crack damage

图7 各工况多裂纹分布示意图Fig.7 Diagram of casesfor multiple cracksdistributions

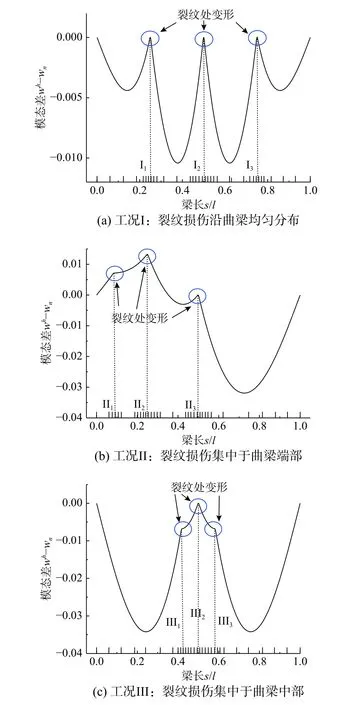
图8 多裂纹损伤下网格分布和屈曲模态差Fig.8 Mesh distribution and buckling modes of circularly curved beam with multiple cracks

5 结论

本文建立了圆弧形曲梁裂纹的截面损伤缺陷比拟方案，实现裂纹的大小(深度)、位置、数目的模拟；针对含裂纹损伤圆弧曲梁弹性屈曲，引入有限元网格自适应分析方法，得到了优化的网格和满足预设误差限的高精度屈曲荷载和屈曲模态解答。经数值算例检验，本文方法对浅梁、深度梁等各类变化几何形式圆弧曲梁的弹性屈曲求解具有良好适用性，解答与解析解具有较高吻合度。研究发现：随着裂纹损伤增大、接近跨中，均会不同程度降低屈曲荷载，越容易诱发弹性失稳。裂纹损伤将诱发屈曲模态变化，本文自适应算法可划分出非均匀网格，在裂纹附近区域使用了相对密集的网格来适应裂纹损伤引起屈曲模态的变化。