城市燃气管网三维度抗震韧性定量评估方法

宗成才，冀 昆，温瑞智，毕熙荣，张晓瑞

(1.中国地震局工程力学研究所，黑龙江，哈尔滨150080；2.中国地震局地震工程与工程振动重点实验室，黑龙江，哈尔滨150080；3.北京市煤气热力工程设计院有限公司，北京100032)

随着当代社会经济的高速发展，仅仅保证城市震后安全已经远远不够，地震作用下尽快实现城市重建、避免出现较大的社会损失变得尤为重要。在该需求下，城市抗震韧性(city seismic resilience)的概念受到广大学者的关注[1-2]。中国2017年将“韧性城乡”列为“国家地震科技创新工程”四大计划之一，以提高我国城市抵御地震风险的能力。作为城市系统的重要子系统，生命线系统具有较高的抗震韧性是保障城市系统基本功能正常的关键，而城市燃气管网作为生命线系统的重要组成部分，在震后引起的管线泄漏，可能引发火灾、爆炸等重大次生灾害，严重影响当地居民的生命财产安全、社会正常生产和生活秩序[3]，因此燃气管网的抗震韧性量化评估值得重点研究。

Bruneau 等[4]将城市(社区)抗震韧性定义为降低地震风险、减轻地震破坏和缩短震后恢复时间的能力，并以鲁棒性(robustness)和快速性(rapidity)作为抗震韧性的评估指标，策略性(resourcefulness)和冗余性(redundancy)作为提高社区抗震韧性的方式，并将这些度量应用到技术维度(technical dimension)，组织维度(organizational dimension)，社会维度(social dimension)以及经济维度(economic dimension)中，通过定义震后目标社区的功能随时间变化的函数实现对抗震韧性的评估。在该框架下衍生出针对交通，供水等多个系统的抗震韧性评估模型[5-7]。而对于燃气管网系统，国外学者对其研究侧重点大多为静态下的抗震性能评估[8-9]，并未对震后燃气管网性能的动态修复环节实现量化评估。Cimellaro等[10]提出了评估燃气管网震后功能恢复的思路与框架，但缺少对燃气管网震后鲁棒性、快速性等指标的量化方法研究。目前国内学者对生命线系统抗震韧性的研究也多集中在供水网络系统[11-14]。Zhao等[11]以供水系统为例，提出适用于一般生命线体系的恢复力双维度综合评估模型，但是并未考虑网络系统震后连通性能的变化过程，也未能刻画出网络系统在整个抗震、恢复过程中各种不确定性因素。

生命线体系抗震韧性各维度是相互依存、相互联系的[4]，如果仅从单一维度对体系进行抗震韧性评价，存在着一定问题。如Chang[15]等对美国孟菲斯地区供水体系进行的抗震韧性定量研究中，该体系在7级地震下技术维度的抗震韧性很弱，但组织维度却表现出很强的抗震韧性，出现了评估结果互不兼容的现象。可见对于城市生命线系统本身，单凭技术或者组织这两者中的任何一维，都无法全面把握目标体系的性能和状态，需要对多个维度抗震韧性进行评估。国内外学者鲜有对燃气管网不同维度的抗震韧性同时进行研究，Cimellaro等[10]仅针对燃气输送效能这一组织维度进行评估，对于其他维度的抗震韧性没有深入研究。

因此，本文首先在课题组现有研究基础之上充分考虑地震动输入和连通性评估的不确定性，基于该地区地震动预测方程为输入依据，通过蒙特卡罗模拟对燃气管网震后连通性进行计算[16]。再通过随机模拟修复资源分配体现修复过程中的不确定性，刻画燃气管网在每次模拟破坏工况下的实时修复进程，进而从技术，组织，社会三维度给出量化指标，并求出概率性能恢复曲线及各个性能水平恢复时间的概率分布。本研究以我国某城市燃气管网作为实例验证了本文三维度抗震韧性量化评估方法的可行性。

1 城市燃气管网三维度抗震韧性定量评估方法

科学合理地考虑地震风险评估中各环节的不确定性是地震风险评估结果可靠的基础[17]。在燃气管网抗震韧性评估过程中：首先，由于燃气管网系统覆盖范围较广，地震动强度评估中需要考虑不同位置处地震动的差异与不确定性。其次，对于宏观的燃气管网系统来说，衡量其性能的是整体的连通性，但是由于关键源点或者管线等可能出现的震后破坏或失效，其连通性状态也会出现较大波动和不确定性。最后，在修复过程中，修复资源的分配及破损管线修复的顺序并不是唯一的，不同修复策略均会对结果有较大影响。

上述地震动不确定性、连通性能不确定性以及修复过程不确定性刻画的分别是地震输入，体系响应以及恢复过程中的不确定性；时间尺度上，刻画震前-震中-震后三个环节里面涉及到的不确定性，以上不确定性会层层传递和累积，造成定量衡量城市燃气管网抗震韧性十分困难。

本文将城市燃气管网抗震韧性量化评估过程分为：管网破坏状态评估，恢复过程模拟以及抗震韧性评估三个环节。下面首先定义燃气管网三维度抗震韧性性能函数；再分别阐述抗震韧性评估过程中三个环节及各不确定性模拟方法；最后给出城市燃气管网三维度抗震韧性量化评估流程。

1.1 三维度性能函数

要实现城市燃气管网的三维度抗震韧性量化评估，首先需要选择适合每一维度物理意义的性能函数。经济维度的抗震韧性评价已经不单单是工程领域问题，涉及较复杂的经济核算及恢复策略，限于篇幅本文不做研究。

生命线系统抗震韧性的技术与组织维度一般从系统层面定义，而社会维度从更加宏观的社区(城市)层面定义[15]。对文献[10-13,15]中供水、供气系统的抗震韧性三维度衡量标准进行梳理后发现：各文献对技术维度与社会维度的衡量标准大体相似，均是震后网络单元的失效比例与功能中断受影响的人口比例。组织维度的衡量标准稍有不同，但均衡量了目标体系预定服务功能或对用户需求满足率损失的程度。对于燃气系统，震后管网连通性可以衡量燃气管网震后的供气服务能力与通气用户的比例(本文燃气网络拓扑结构中每一个用户节点，都是小区级别的调压站，文中的通气用户比例实际上指的是连通的调压站节点的比例)，可以作为燃气管网抗震韧性组织维度的衡量标准。

因此，结合上述三维度的内涵，给出城市燃气管网技术、组织、社会维度的性能函数，分别为式(1)～式(3)，不同维度性能衡量原则与函数的物理意义如表1所示。

式中：Ns、ns分别为地震前后未失效门站数；Np、np分别为地震前后未失效管线数；w1、w2为门站与管线重要性因子：w1+w2=1，w1、w2的大小可由相关政府决策人员根据实际情况取值，本文暂各取0.5；

式中，Npre、npos地震作用前后，可以接收到燃气的用户数量：

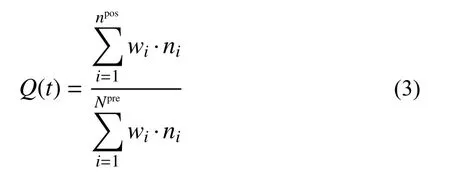
式中：wi代表用户i重要性程度的系数；(如医院、学校、重要交通枢纽等w取为1.5，普通用户取值1)；ni为用户i所覆盖的人口密度。

表 1燃气管网不同维度性能衡量原则与函数物理意义Table 1 Principles of measuring performance and physical meaningsof performance function for gasnetwork in different dimensions

虽然技术与组织维度均从系统层面定义，都是燃气管网自身性能的体现。但是技术维度是指燃气管网各单元物理性能的破坏，而组织维度不仅取决于单元物理破坏的程度，还取决于各单元组成的整体拓扑结构。相比于技术维度，组织维度反映了网络的冗余程度，其恢复效率也能更好的反映出政府决策者的组织协调、应急部署能力。

1.2 燃气管网破坏状态评估

首先，以燃气管网所在区域的某一历史地震或者目标活跃断层的位置作为假想震源，通过联立求解长、短轴地震动土层预测方程得到该市燃气管网各节点的PGA、PGV 单次模拟值，其中用服从正态分布的随机数模拟地震动预测方程中的不确定性(随机误差)。进行N次蒙特卡罗模拟，得到考虑地震动不确定性的不同地震动输入工况。在每一次模拟中，燃气管网门站失效概率与埋地管线的平均震害率也均不相同，采用各单元产生随机数的方式模拟网络各单元的失效，生成新的受损网络，计算每一次模拟工况下的燃气管网震后连通性状况。再根据第1.1节式(1)～式(3)中性能函数的定义，求出对应的不同维度的性能下降值。课题组基于该套蒙特卡罗模拟方法进行了某城市的燃气管网连通易损性评估，参考文献[16]。

与易损性评估时管线失效模拟的差异在于：由于某根埋地管线的破裂数对修复时间有影响，因此抗震韧性评估时埋地管线的失效应模拟出相应的破裂数，采用文献[18]方法。

埋地管线的破坏可以假定为沿管线服从参数为Rf(管线平均震害率)的泊松分布[18]，每根埋地管线从管线接口到第一处破裂点或连续两处破裂点的间距Dj服从参数为Rf的指数分布：

1.3 恢复过程随机模拟

N次模拟工况下的燃气管网破坏状态不尽相同，与之对应的是N个不同的性能恢复过程，本文采取先门站再管线的修复顺序[19]，其中门站的修复时间可以结合实际建筑类型等情况设定为固定天数，下面重点讨论不确定性较大的管线修复时间与修复顺序。

恢复过程暂不考虑重新埋设管线的情况，仅考虑对破裂管线进行修复。如果缺乏当地关于抢修效率的足够资料，HAZUS-MH-MR4中假设震后抢修管线时间服从正态分布[20]：一个完整的施工组抢修渗漏、接口破坏类型的破裂点所需时间服从N～(6 h，3 h)，抢修断裂破坏类型的破裂点所需时间服从N～(12 h，6 h)，依据该分布可以对修复时间进行随机抽样模拟。管道修复顺序可以采用随机策略，即对各条破损管道抢修顺序是随机生成的，比较符合震后无序的状态[13]；也可以采用阈值法对某区域进行优先排查和检修。可以假设每个施工组每天的抢修工作时间为12 h，非抢占式修复。根据实际情况预先设定好施工组的数量，对修复时间和修复顺序进行随机抽样，即可计算得到燃气管网某次模拟工况下的三维度性能实时恢复的进程，并绘制出该次模拟下三维度的性能恢复曲线Q(t)，如图1所示。

图1 单次模拟燃气管网恢复曲线示意图Fig.1 Schematic diagram of gas network recovery curve in a single simulation

1.4 韧性评估指标计算

图1中的纵坐标Q(t)代表时间t时的燃气管网性能。当Q(t)=0时代表整个燃气管网该维度性能彻底瘫痪，Q(t)=100%代表性能水平恢复至震前。地震发生时刻(t0)和修复中某一时刻(tR)的燃气管网性能水平分别用Q(t0)和Q(tR)表示。了体系恢复力的大小。这里假设燃气管网正常运行时性能水平维持100%不变，且性能恢复水平最多达到震前水平，恢复力可用式(5)简化表示。可以看到恢复力的本质就是性能恢复函数与时间轴围成面积与修复时间段的比值。恢复力是对整个燃气管网系统性能恢复能力进行评价的一个综合量度指标，可以对任意修复时间，任意状态下的燃气管网抗震韧性进行评价。

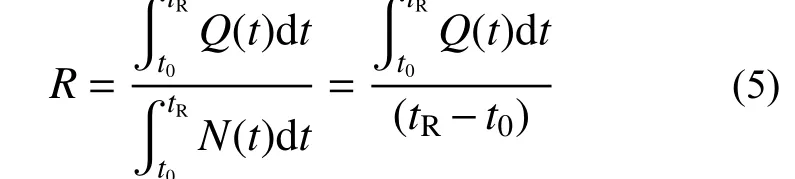
作为韧性量化评估的两个具体指标：鲁棒性指标和快速性指标，定义了震后性能(q0)和修复速率(v)两个指标分别反映燃气管网震后的性能残余值以及震后的性能恢复速率，计算公式分别为式(6)、式(7)，两个韧性指标的物理意义如表2所示。

表2 燃气管网不同韧性指标物理意义Table 2 The physical meaningsof different resilience indexes of gas network

单次模拟过程中的恢复力、鲁棒性和快速性指标结果，并不能刻画燃气管网的抗震韧性。重复N次模拟，可得到N条性能恢复曲线组成的曲线簇。依据式(5)～式(7)分别计算每条性能恢复曲线的恢复力、震后性能和修复速率。通过对多次模拟工况下的上述指标求均值与标准差，即可得到相应指标的期望估计值与离散性。

最后将三个维度恢复力(或者某一具体指标)均值加权相加，便可以得到综合了物理单元震害、供气服务能力以及社会影响三方面的城市燃气管网抗震韧性的整体评价指标，其中不同维度的权重可以根据政府决策者权衡各维度的重要性而定。至此，整个燃气管网系统三维度下的抗震韧性量化评估流程完成，如图2所示。

2 燃气管网三维度抗震韧性定量评估实例

本节选取了文献[16]中国华北某城市部分燃气管网作为算例，应用上文的抗震韧性评估流程对该市燃气管网的技术维度、组织维度、社会维度进行抗震韧性评估，其中各用户节点覆盖人口密度依据该市人口密度分布图确定。

2.1 燃气管网拓扑建模

对该市的燃气管网进行拓扑网络的构建，如图3所示。其中共9个燃气门站，110个用户。门站编号分别为：3、85、117、157、170、178、254、297、299。共306个节点、326条边，燃气管道总长1037.1 km，部分管段信息参考文献[16]。本文以该市历史发生过破坏性地震的某个活断层为假想震源所在断层(如图3所示)，其长轴方向依据所在活动断层走向确定，设定地震震级为8级。由于工程场地勘测钻孔资料的缺失，本文暂不考虑燃气管网所在地区的场地类型差异。

2.2 抗震韧性定量评估结果

应用1.2节式(4)计算燃气管线的破坏。燃气管线在震后以渗漏、接口破坏最为常见，而在液化区或断层附近管体断裂破坏也较为突出[21-23]。由该市的地质勘测资料可知，A 区、B区是地震崩塌高发区，假设震后A 区、B区管线为断裂破坏，其他区域均为渗漏破坏。假设该市具有3个完整的施工组，按照先门站再管线的顺序进行修复[19]，管线修复顺序采取随机策略。假设门站的修复时间为3 d，这样假设：一是比较符合实际情况[19]；二是可以将门站与管线分别修复对体系性能的提升度体现出来。

2.2.1单次模拟三维度性能恢复曲线

图4是某次模拟下，燃气管网三维度性能恢复曲线，它是针对某次震害工况下恢复进程的模拟。从图4可以看到：该次震害下，该市燃气管网的技术维度、组织维度、社会维度性能分别下降到了约为震前水平的73%、47%、52%，组织维度的鲁棒性最差。当3 d 后85号、254号、297号、299号四个在震后失效的燃气门站被修复后，三维度性能分别提升到了约95%、63%、72%，随后三个施工组进行管线修复。共花费13 d 时间将该市燃气管线三维度性能恢复至震前水平。需要注意的是，图中椭圆范围显示修复某段或者某几段管线对同是基于连通性的组织维度和社会维度的性能提升程度并不一致，也即不同管线对不同维度的重要程度是不同的。该结果也警示决策者，在地震发生后，要权衡不同维度的重要性，选择对某维度重要程度更大的管线优先修复。

2.2.2韧性指标计算

图2 城市燃气管网抗震韧性评估流程Fig.2 Seismic resilience evaluation process of urban gas network

该市燃气管网500次模拟结果下的恢复曲线如图5所示，图中给出了均值曲线和加减一倍标准差的分布结果。从图中可以看出单次模拟下的燃气管网技术维度恢复曲线大致呈直线型上升，最后管道修复过程中的均值性能恢复曲线也基本呈线性，这主要是因为技术维度依据的是地震前后未失效门站与管线数的比例，受修复资源的分配方式影响较小，在修复资源一定时，基本与时间是线性关系。而组织与社会维度的恢复曲线由于是基于管网连通性计算的，受修复顺序与资源分配影响较大，单次恢复曲线呈阶梯状，其均值恢复曲线呈先线性上升，后曲线上升的趋势。本案例中，大致在震后12 d 左右(图6(a))，燃气管网在这两个维度下的性能恢复速率出现显著下降。

应用1.4节式(5)～式(7)计算该市燃气管网技术，组织以及社会维度下500次模拟结果的震后性能以及完全恢复时体系恢复力和修复速率，并计算三者的期望值。从图6(b)可以看出该市燃气管网在该次设定地震作用下，三维度下震后性能水平约为70%、32%和34%，技术维度下的鲁棒性最强，而与管网连通性相关的组织与社会维度的鲁棒性最差，这意味着如果不考虑网络连通性，仅仅简单依据地震前后未失效门站与管线比例，对实际的震后灾害后果是较为低估的。通过修复速率指标可以看出，该市在震后技术维度性能每天恢复大约2%，其他两维度性能每天恢复约5%。技术维度下的恢复力期望值约为0.9，比其余两个维度接近0.7的恢复力期望要大很多。以上指标的计算结果对比说明考虑燃气管网的连通性，并从多个维度客观量化评价抗震韧性的重要性。

图3 该市燃气管网简化网络图Fig.3 Simplified network diagram of the city'sgas network

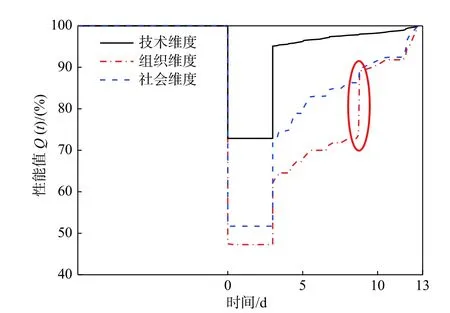
图4 该市燃气管网单次模拟下三维度性能恢复曲线Fig.4 Three-dimensional recovery curves of the city'sgas network in a single simulation

图5 该市燃气管网三维度性能恢复曲线Fig.5 Three-dimensional recovery curves of thecity'sgasnetwork

图6 该市燃气管网三维度均值恢复曲线和韧性指标Fig.6 Three-dimensional mean recovery curves of the city's gasnetwork and resilience index expectations

本文将各维度权重均定为1/3，对该市燃气管网进行整体评价。其中鲁棒性指标约为45%，完全恢复时体系快速性指标约为4%，恢复力为76%，总体来看，该市燃气管网的抗震韧性较好。

上述结果表明：与Cimellaro等[10]采用的仅从输送效能这一组织维度对燃气管网进行的抗震韧性评估方法相比，虽然本文需要在评估工作前收集相对更多的数据(诸如人口密度与建筑物重要性等)，需要进行更多次的蒙特卡罗模拟，但是相较于文献[10]中流量的计算，本文采用的连通性评估，其数学模型却相对简单，并且从评估结果来看，本文考虑各类不确定性的多维度抗震韧性评估方法，从单元物理震害、供气服务能力、社会人口影响等多个方面对城市燃气管网的抗震韧性进行了概率意义上的综合评估，从单一体系上升到社区(城市)层面，能够更加全面把握目标体系的震后的状态、性能以及社会影响。

2.2.3统计分布规律与最优施工组数量确定

经K-S检验，该市燃气管线的震后性能和门站全部恢复时的三维度性能水平均在显著性水平α=0.01时服从正态分布，结果如图7所示。燃气门站修复完成对该市燃气管网的三维度的性能提升度分别约为25%、21%、23%。

图7 震后即时与震后3 d 燃气管网三维度性能分布图Fig.7 Three-dimensional performance distribution maps of the gas network immediately after the earthquake and threedaysafter theearthquake

对该市燃气管网性能达到不同恢复程度的时间进行统计(图8)，在显著性水平α=0.01时，组织和社会维度75%、90%、完全恢复的时间均通过了对数正态分布检验。这里需要指出的是，我们剔除了组织维度在震后三天门站修复完成其性能值就已达到75%的11个特殊的模拟工况。两维度恢复75%、90%、完全恢复的时间期望差异不大，约为7 d、10 d、13 d(图9)。

图8 该市燃气管网不同恢复程度恢复时间分布图Fig.8 Recovery time distribution maps of different recovery levels for the city's gas network

图9 该市燃气管网不同恢复程度恢复时间分布箱型图Fig.9 Recovery time distribution box diagrams of different recovery levels for the city's gas network

本研究同样对该次设定地震下不同施工组数量对恢复时间的影响进行研究。结果显示，不同数量施工组在组织维度与社会维度75%、90%的恢复程度的恢复时间也满足显著性水平α=0.01下的对数正态分布检验。而完全恢复时间在1个～6个施工组参与修复工作时也通过对数正态分布检验，而大于6个施工组时，由于出现怠工的情况，故大多数均未通过对数正态分布检验。

不同数量施工组参与修复时不同恢复程度所对应的的恢复时间均值与标准差如图10所示。图中恢复时间均值曲线呈凹型，由此可见在施工组较少时，性能恢复时间随施工组数量增加下降迅速，之后性能恢复时间达到稳定值，无论施工组数量如何增加，均无法降低恢复时间。因此，对于施工组的投入，应考虑饱和效应，控制施工组数量使其达到最优投入量，以达到相对投入较少，收益较高的目的。图10中恢复时间均值曲线从下降段达到平稳段时施工组数量的拐点，便是该市燃气管网该次设定地震下的最优施工组数量：6个。

图10 不同数量施工组参与修复时在不同恢复程度时所对应的恢复时间均值与标准差Fig.10 Mean and standard deviationsof recovery time corresponding to different recovery levels for different numbers of repair team

国内除汶川地震外，目前尚未有大城市现代燃气管网大面积震害的实例。将本文计算结果与汶川8.0级地震时，属于9度烈度区的都江堰市管网震后抢险救灾结果作对比[19]。都江堰市燃气管网总长度500 km，约为本文案例城市的一半，因缺少都江堰市实际震害时的管线震害率、与连通性损失等数据，因此仅就在相同施工组投入修复工作时的通气恢复时间做了对比：都江堰市发生地震后，共投入五家公司(假设是投入五个施工组)抢险救灾人员进行修复工作，震后5 d～9 d 基本恢复城区供气，由图10结果可知，在五个施工队时，案例城市完全恢复供气的时间均值约为11 d，标准差约为3.5 d，综合考量烈度与管网尺度大小，本文计算结果具有一定的可靠性。

3 结论

本文提出了城市燃气管网三维度抗震韧性量化评估方法，并给出了我国某城市的燃气管网三维度抗震韧性评估实例。评估思路与结论总结如下：

(1)在某设定地震下，首先，衔接GMPE 输入，通过蒙特卡罗模拟对燃气管网连通性进行计算；基于燃气管网三维度性能函数，完成燃气管网不同维度在震后破坏状态评估；再根据所评估地区所具备的恢复条件，得到单次模拟下的三维度性能恢复曲线；最后通过N次的蒙特卡罗模拟，得到该市燃气管网均值恢复曲线及各韧性评价指标期望估计值。

(2)技术维度依据的是地震前后未失效门站与管线数的比例，受修复资源的分配方式影响较小，在资源量一定时，基本与时间是线性关系。而组织与社会维度的恢复曲线是基于管网连通性计算的，受修复顺序与资源分配影响较大，其均值恢复曲线呈先线性上升，后曲线上升的趋势。技术维度下的鲁棒性最强，而与管网连通性相关的组织与社会维度的鲁棒性最差。这说明如果不考虑网络连通性，对实际的震后灾害后果是较为低估的，说明从多个维度客观量化评价抗震韧性的重要性。综合考虑三个维度影响，该市燃气管网整体恢复力约为76%，抗震韧性较好。

(3)就本文所研究的燃气管网案例而言，震后三维度的残余性能值存在差异，但均服从正态分布；组织维度和社会维度性能恢复75%、90%以及完全恢复的时间服从对数正态分布，期望值约为7 d、10 d、13 d。通过对比不同数量施工组修复时的恢复时间期望，得到该市震后最佳施工组数量大致为6个，继续增加施工组数量对性能修复速率提升较小。

本文所提出的方法可以对任意假想地震下目标城市的燃气管网系统的抗震韧性进行评估，不仅可以用于灾后模拟，紧急处置预演，还可以用于灾前统筹资源，管网规划评估。所关心的三个韧性维度可以全方位展现燃气管网的抗震能力与紧急处置效果，方便决策者根据当地的经济水平，因地制宜，因城施策，具有较好的工程应用价值。该评估思路同样可以推广至其他生命线网络系统，如供水系统，供电系统，为其他网络系统抗震韧性定量评估提供借鉴。