新型旋转放大式黏弹性阻尼器性能试验研究

李宏男，李元龙，黄 宙，付 兴

(1.大连理工大学海岸和近海工程国家重点实验室，辽宁，大连 116024；2.沈阳建筑大学土木工程学院，辽宁，沈阳110168)

被动控制一般是指对结构的某些部位进行改造处理，或在结构的某些位置设置特种机构、隔振装置、附加子结构等实现隔振和耗能，从而减小结构的动力响应[1-4]。阻尼器是一种典型的被动控制元件，通过滞回变形耗散地震或风荷载等输入到结构中的能量，达到保护结构安全的目的[5-8]。框架结构在外荷载作用下梁柱节点的受力机理复杂，节点区域是结构的核心部位，常常也是薄弱环节，在梁柱节点处设置转角式节点阻尼器是一种经济适用、耐久高效的保护方法。在外荷载作用下梁柱节点的转角变形带动阻尼器发生滞回变形实现耗能减震的效果，有利于提高结构的整体安全稳定性，符合结构抗震中的延性设计理念[9]。

Martinelli和Mulas[10]提出了一种以能量耗散为目标的无源被动控制技术，即采用基于摩擦、金属屈服、粘弹性固体和流体变形的能量耗散装置，通过在梁柱节点周围设置该转动摩擦耗能装置来提高结构阻尼，可用于框架结构的抗震设计和加固。Soydan 等[11]研究了一种基于在预制钢筋混凝土框架结构梁柱节点区域设置铅挤压阻尼器的新型改造加固方式，进行了1/2缩尺比不加固和加固结构模型的振动台试验以及非线性动力时程仿真分析，结果表明设置铅挤压阻尼器后，预制框架层位移、层间位移角、弯矩和柱基处的塑性变形均明显降低。吴丛晓等[12]设计制作了一种利用铅和橡胶两种耗能材料同时工作的扇形铅黏弹性阻尼器，研究了该阻尼器的滞回曲线、骨架曲线与恢复力模型、疲劳性能及大变形能力等，并进行了有限元分析。王艮平等[13]提出了采用扇形铅黏弹性阻尼器加固框架结构的方法，设计并制作了无控框架和两榀不同连接方式的扇形铅黏弹性阻尼器加固框架，通过低周往复加载试验分析了其滞回性能、承载能力、刚度退化、耗能能力等指标，验证了其加固效果。邹爽等[14]提出了一种适用于村镇木框架结构房屋的新型角位移黏弹性阻尼器，进行了力学试验及低周期疲劳性能试验，探究了在不同温度、加载频率和加载位移下各力学性能指标的变化规律。

然而，钢筋混凝土框架结构在外荷载作用下梁柱节点处产生的转角变形一般较小，传统的节点转角式阻尼器只有当梁柱节点处发生较大的相对转角时才能充分发挥其耗能减震能力，在小变形情况下难以达到理想的耗能效果，实际工程应用中存在一定的局限性。为此，本文提出了一种新型旋转放大式黏弹性阻尼器(rotation-magnified viscoelastic damper，简称RMVD)，利用杠杆原理将梁柱节点处相对较小的转角变形进行放大，从而增大黏弹性材料的滞回变形耗能，可有效提高对结构的振动控制能力。首先介绍了RMVD 的基本构造及工作原理，并加工制作了实物模型，对其进行不同工况下的循环加载试验以及疲劳试验，探究各力学性能指标随加载频率和转角变形幅值的变化规律；并与相同试验工况下传统无放大功能转角阻尼器的耗能效果进行对比分析，验证了RMVD的耗能放大能力。

1 阻尼器基本构造及工作原理

1.1 基本构造

本文提出的新型旋转放大式黏弹性阻尼器构造示意图如图1所示，三维结构图如图2所示，主要构件尺寸图如图3所示。该阻尼器主要由以下部分构成：1—侧板；2—底板；3—转轴；4—内扇形支撑板；5—外扇形支撑板；6—扇形旋转剪切板；7—圆角矩形滑槽；8—12.9级高强螺杆；9—橡胶板(采用20 mm 厚的高阻尼丁基橡胶，其复合剪切模量为0.51 MPa)。

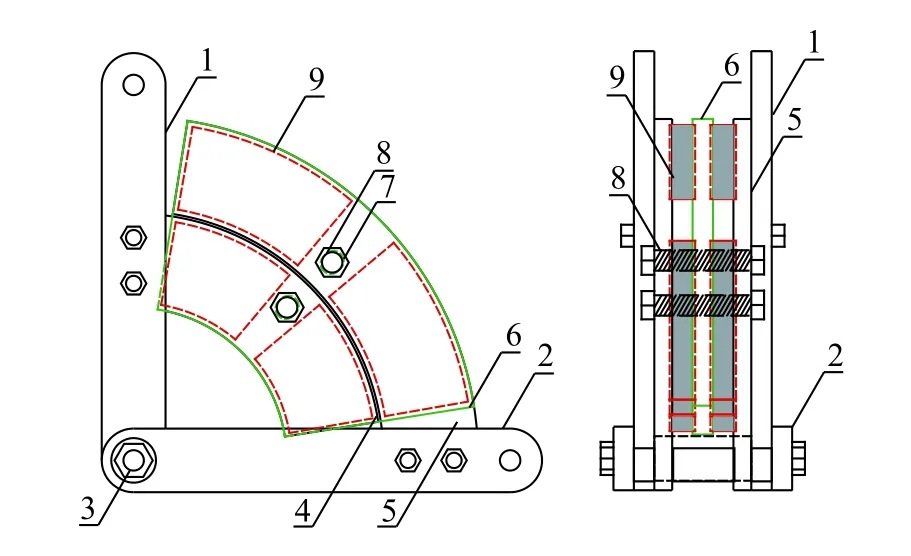
图1 旋转放大式黏弹性阻尼器构造示意图Fig.1 Construction diagram of the RMVD

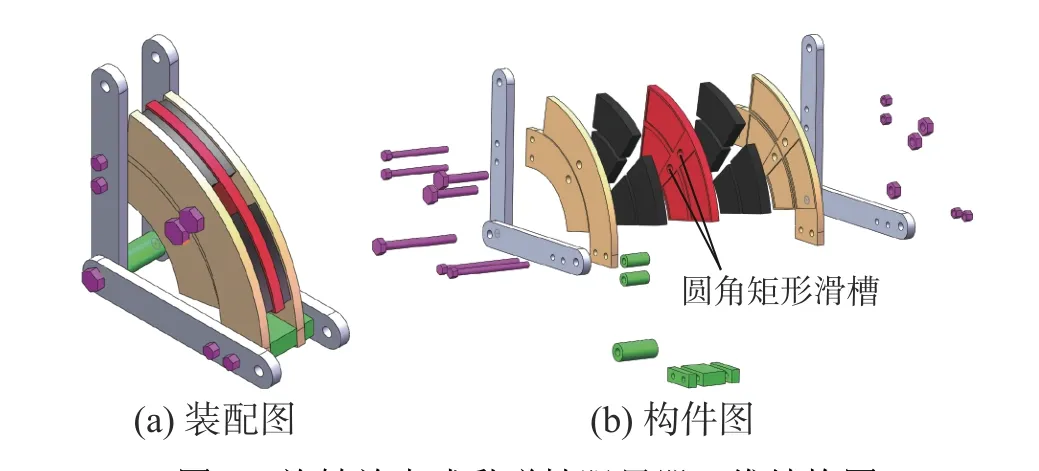
图2 旋转放大式黏弹性阻尼器三维结构图Fig.2 The three-dimensional structure diagram of the RMVD

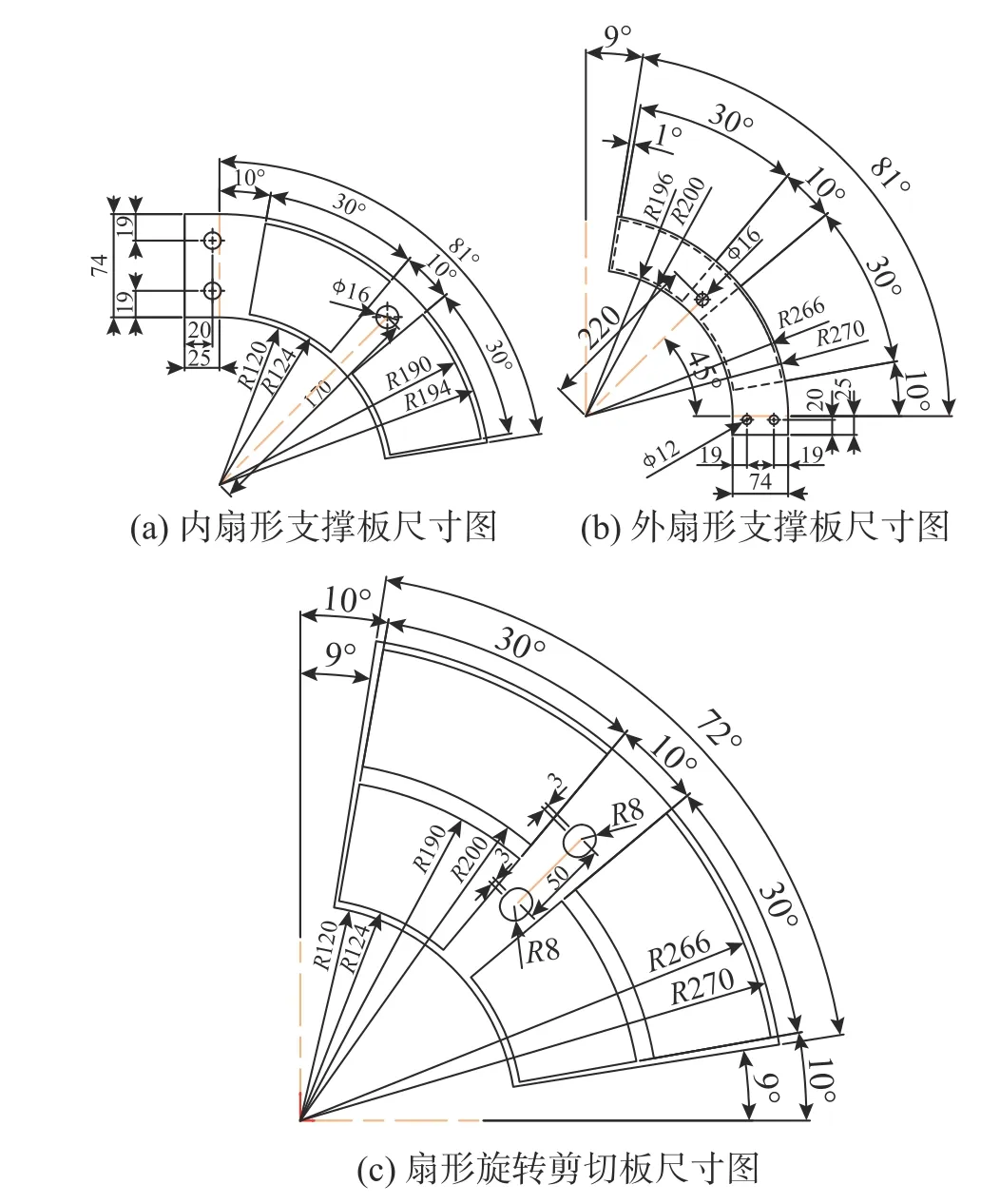
图3 旋转放大式黏弹性阻尼器主要构件尺寸图Fig.3 The main component dimension diagram of the RMVD

侧板1和底板2通过转轴3铰接，内扇形支撑板4、外扇形支撑板5分别通过螺栓和套块固接在侧板1和底板2上。为保证阻尼器绕转轴3转动使橡胶板9发生剪切变形，内扇形支撑板4、外扇形支撑板5 及扇形旋转剪切板6的圆心均应为转轴3。在内扇形支撑板4、外扇形支撑板5上相应位置开圆孔，在扇形旋转剪切板6相应位置开2个圆角矩形滑槽7，用12.9级高强螺杆8穿过内、外扇形支撑板和扇形旋转剪切板，实现铰接。在内、外扇形支撑板与扇形旋转剪切板之间设置橡胶板9，用环氧树脂高强胶黏剂牢固粘结。考虑到阻尼器中橡胶会产生较大的剪切变形，故在内、外扇形支撑板和扇形旋转剪切板之间设置橡胶板的相应位置开设2 mm 凹槽，凹槽的设计可以确保阻尼器工作时橡胶板发生纯剪切变形，且可以保证橡胶板与两侧钢板粘结更牢固，防止其在大变形情况下开裂脱落。该阻尼器所用钢材均为Q345钢，实物图如图4所示。

1.2 工作原理

该阻尼器可直接安装在框架结构的梁柱节点区域，通过预留孔洞用螺杆将侧板和底板与梁柱固定连接，工程安装示意图如图5所示，工作原理示意图如图6所示。当结构梁柱节点变形带动侧板和底板旋转时，阻尼器的内、外扇形支撑板相对转动，促使高强螺杆沿圆角矩形滑槽运动，在高强螺杆的驱动下，扇形旋转剪切板的转角可成倍放大，从而使橡胶板产生更大的剪切变形，充分发挥其滞回耗能能力，达到更理想的耗能减震效果。

图4 旋转放大式黏弹性阻尼器照片Fig.4 Photo of the RMVD

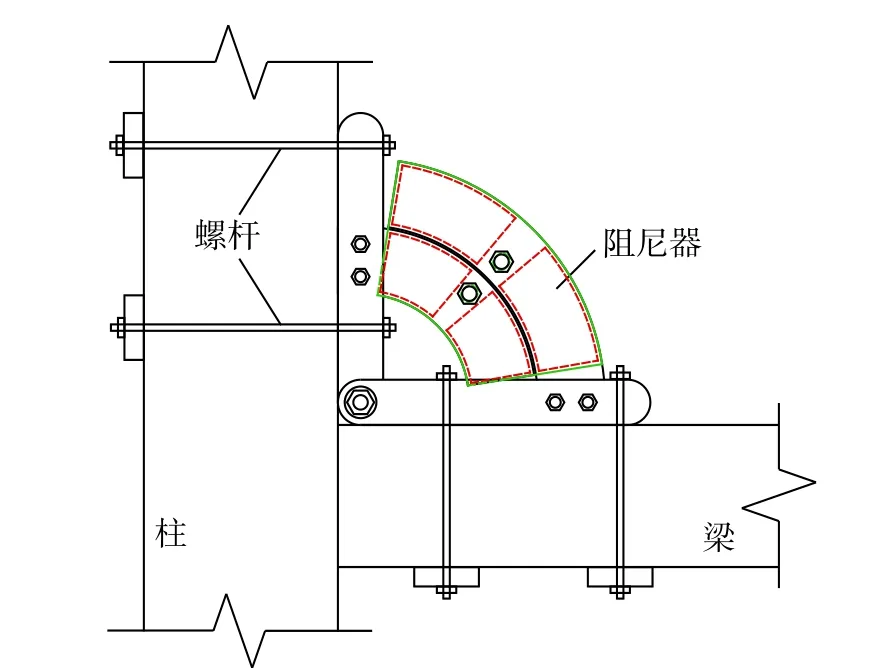
图5 旋转放大式黏弹性阻尼器工程安装示意图Fig.5 Engineering installation diagram of the RMVD

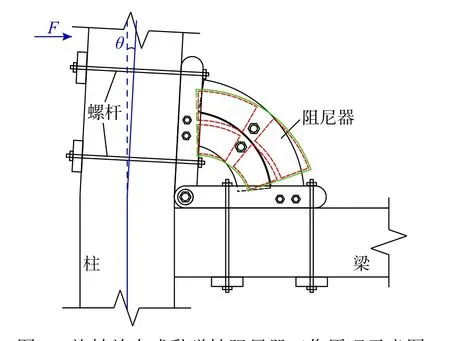
图6 旋转放大式黏弹性阻尼器工作原理示意图Fig.6 Working principle diagram of the RMVD

该阻尼器的转角放大示意图如图7所示，两圆角矩形滑槽中心A、B距阻尼器旋转中心O的距离分别是x和y，本文中x取17 cm，y取22 cm，OAB连线与水平方向夹角为π/4。当结构梁柱节点转动α 时，A、B的位置变化到A′、B′，产生的相对转角γ 为：

图7 旋转放大式黏弹性阻尼器转角放大示意图Fig.7 Angle magnification diagram of the RMVD

则转角放大倍数m为：

该阻尼器不同转角对应的放大倍数如表1所示，可以看出所设计的阻尼器转角放大倍数稳定在3.8～3.9，橡胶板的剪切变形实现有效放大。

表1 转角放大倍数计算表Table 1 Angle magnification calculation table

根据建筑结构的实际情况，可采用以下两种方法调节阻尼器的耗能放大能力：1)调整高强螺杆8的开孔安装位置；2)调整橡胶板9的粘结位置和尺寸。

2 试验概况

2.1 加载方案

加载设备采用MTS电液伺服作动器，最大负荷为100 kN。试验目的是研究加载频率和转角变形幅值对阻尼器滞回性能的影响，采用位移控制加载方式，同一加载条件下，作5次具有稳定滞回曲线的循环，选择第3次循环时滞回曲线的数据作为实测值，疲劳性能试验连续加载30圈[15-18]。试验过程中环境温度保持在23±2℃，力学性能试验在大连理工大学结构监控研究所实验室进行，试验装置如图8所示。

图8 旋转放大式黏弹性阻尼器试验加载图Fig.8 Test loading diagram of the RMVD

试验加载方案如表2所示，每完成一个工况试验后，仔细检查阻尼器是否破坏，橡胶与钢板之间的粘结是否有剥离损坏的情况，若完好无损则继续进行试验。每个工况加载结束后将试件静置15 min，疲劳试验结束后静置60 min，然后再进行下一个工况的试验。

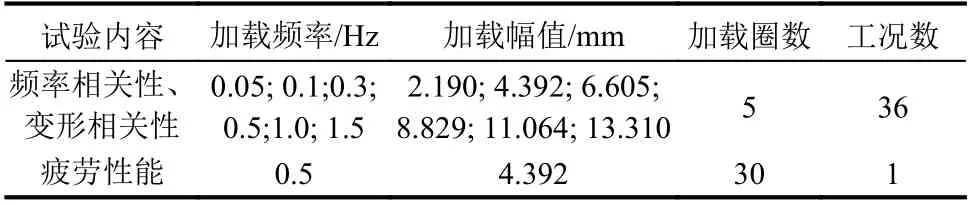
表 2试验加载方案表Table 2 Table of test loading scheme

图9给出了试验过程中该阻尼器几何变形关系图，H(值为270 mm)是从旋转轴中心到加载点中心的距离，L是两个加载点间的初始距离。阻尼器侧板和底板之间的初始弧度为β(值为π/2)。当MTS试验机施加力F时(正负力情况相同)，阻尼器两个加载点的竖向相对位移为Δ，两个加载点间的距离将变为L-Δ；侧板和底板绕转轴旋转弧度为θ，其夹角将变为β-θ。两个加载点L之间的初始距离为：

旋转弧度θ 为：

通过试验数据F、Δ计算得到M、θ，从而得到阻尼器的弯矩-转角滞回曲线。

需要说明，试验数据处理时转角均采用弧度制，但为更直观的描述试验现象，在下文阐述各力学性能指标的变化规律时采用角度值，阻尼器试验过程中加载幅值、旋转弧度及角度的对应关系如表3所示。

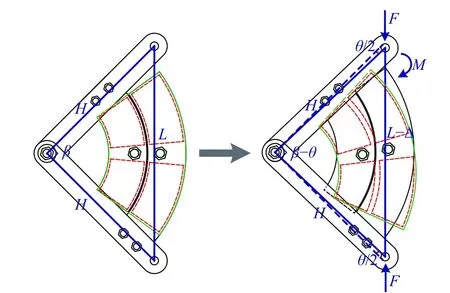
图9 循环加载试验旋转放大式黏弹性阻尼器几何变形关系图Fig.9 Geometric deformation diagram of the RMVD for cycly loading test

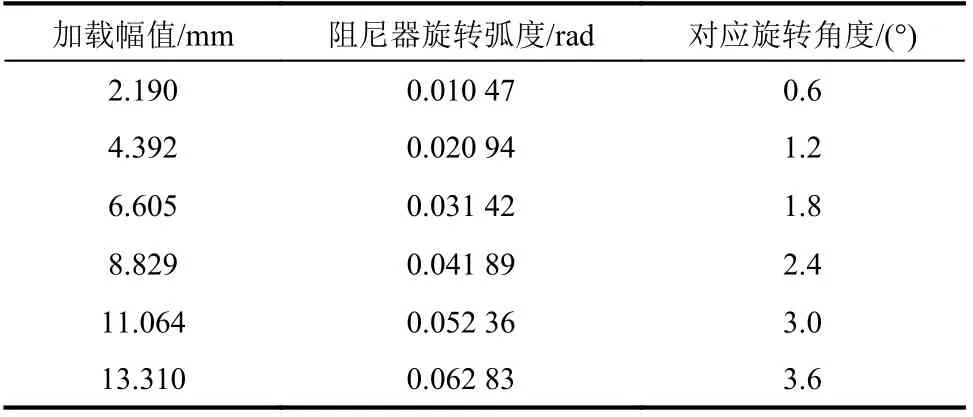
表3 阻尼器试验过程中参数对应表Table 3 Corresponding tableof parametersin RMVD test

2.2 力学性能指标选取

根据《建筑消能阻尼器》(JG/T 209-2012)中对黏弹性阻尼器力学性能和疲劳性能的相关规定，选取最大阻尼力P、等效剪切刚度K、等效粘滞阻尼比ξ 和每循环耗能ΔW等指标[19-20]来评价该阻尼器在不同加载工况下的力学性能。各力学性能指标定义如下：

3 试验结果分析

3.1 试验现象

试件在所有加载工况下工作性能稳定，试验过程中钢板平整无破损，高强螺杆无弯剪破坏，高阻尼橡胶表面平整密实、无任何破坏迹象，橡胶与钢板粘结良好。

3.2 频率相关性

控制加载幅值为2.190 mm、4.392 mm、6.605 mm、8.829 mm、11.064 mm 和13.310 mm，加载频率依次取0.05 Hz、0.1 Hz、0.3 Hz、0.5 Hz、1.0 Hz 和1.5 Hz 分别进行加载试验，研究该阻尼器各力学性能随加载频率的变化规律。图10为该阻尼器频率相关性试验的滞回曲线，可以发现其不同加载频率工况下的滞回曲线饱满稳定，随加载频率的提高滞回环面积增加，曲线更加光滑，耗能能力逐渐增强。

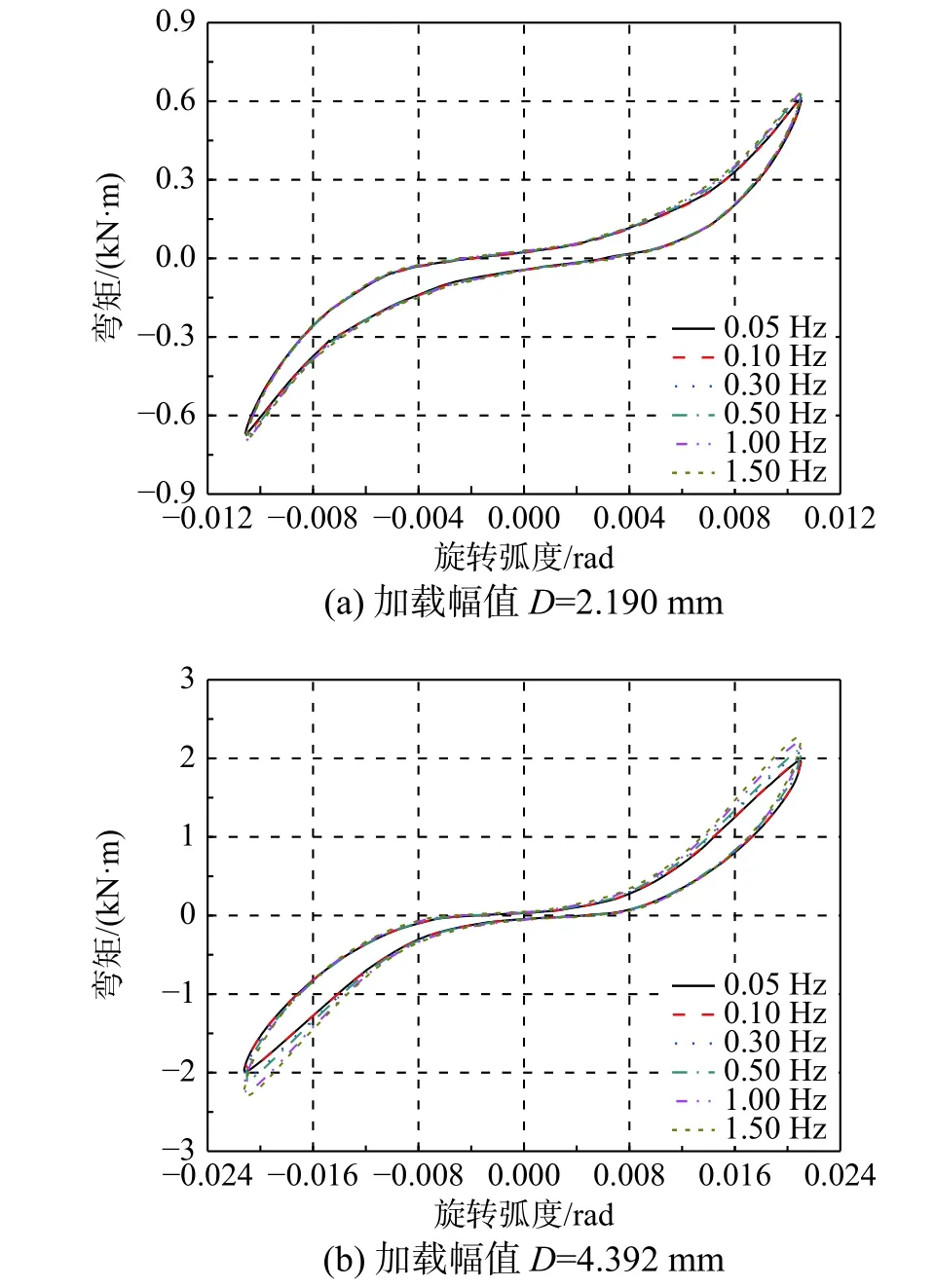
图10 频率相关性试验滞回曲线Fig.10 Hysteretic curve of frequency dependency test

图11给出了该阻尼器的主要力学性能指标随加载频率的变化规律曲线，包括最大阻尼力P、等效剪切刚度K、每循环耗能ΔW和等效粘滞阻尼比ξ。由图11(a)可以看出当阻尼器旋转角度较小时，最大阻尼力P随加载频率的提高变化很小，旋转角度越大时P增大的越快，当旋转角度为0.6°时，P的增幅为4.11%，而当旋转角度为3.6°时，P的增幅达到30.48%。由图11(b)可以看出等效剪切刚度K随加载频率的提高逐渐增大，但当旋转角度为0.6°时，增加不明显，当旋转角度为3.0°和3.6°时，K增幅较接近。由图11(c)可以看出当阻尼器旋转角度小于1.2°时，每循环耗能ΔW随加载频率的提高几乎保持不变，当旋转角度大于1.8°时，ΔW持续增大，该阻尼器的耗能能力不断増强；控制旋转角度为3.6°、加载频率为0.05 Hz 时，ΔW为122.773 kN·m·rad，加载频率为1.5 Hz 时，ΔW为237.613 kN·m·rad，耗能增幅高达93.54%。由图11(d)可以看出随加载频率的提高等效粘滞阻尼比ξ 急剧增长；当阻尼器旋转角度为3.6°、加载频率从0.05 Hz 增加到1.5 Hz时，ξ 提高1.54倍。

综上说明，当阻尼器旋转角度越大时，各力学性能的频率相关性越显著，加载频率越高其耗能效果越好。

3.3 变形相关性

控制加载频率为0.05 Hz、0.1 Hz、0.3 Hz、0.5 Hz、 1.0 Hz 和1.5 Hz， 加载幅值依次取2.190 mm、4.392 mm、6.605 mm、8.829 mm、11.064 mm 和13.310 mm 分别进行加载试验，研究该阻尼器各力学性能随加载幅值的变化规律。图12为该阻尼器变形相关性试验的滞回曲线，可以发现其不同旋转角度的滞回曲线饱满稳定，随阻尼器旋转角度的增大滞回环面积越大，耗能效果越好。

图13给出了该阻尼器各力学性能指标随其旋转角度的变化规律曲线。由图13(a)可以看出最大阻尼力P随阻尼器旋转角度的增加逐渐增大，但增长速度逐渐降低，当阻尼器旋转角度从0.6°增大到3.6°时，不同加载频率下P增幅均超过1110.64%。由图13(b)可以看出当阻尼器旋转角度小于1.8°时，等效剪切刚度K急剧增大；当大于1.8°时，K缓慢减小，表现出一定程度的刚度退化。由图13(c)可以看出，随阻尼器旋转角度的增加每循环耗能ΔW逐渐增大，且增长速度越来越快；旋转角度增加0.6°时，ΔW的最大增值为20.215 kN·mm·rad。由图13(d)可以看出，等效粘滞阻尼比ξ 随旋转角度的增加呈现出先微弱减小后持续增大的趋势，旋转角度为1.2°时，ξ 达到最小值。

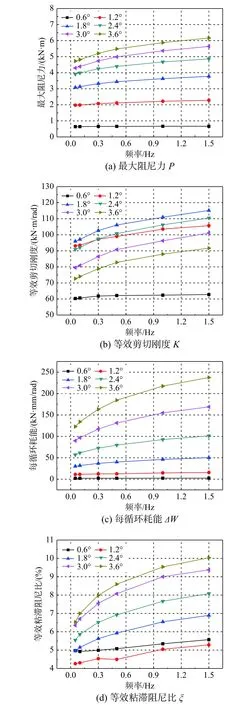
图11 力学性能指标的频率相关性变化规律曲线Fig.11 Frequency dependency variation law curve of mechanical properties index

上述结果表明，该阻尼器在不同加载频率下，各力学性能的变形相关性显著，阻尼器旋转角度越大其耗能效果越好。

3.4 疲劳性能

为研究该阻尼器的疲劳性能，对试件进行频率为0.05 Hz、幅值为4.392 mm 的30圈循环加载[21]，图14为疲劳性能试验的滞回曲线。由图14可以发现，经过30圈循环加载后，该阻尼器滞回曲线依旧对称稳定、变化微弱，仍然保持良好的耗能效果，耗能能力衰减很小。

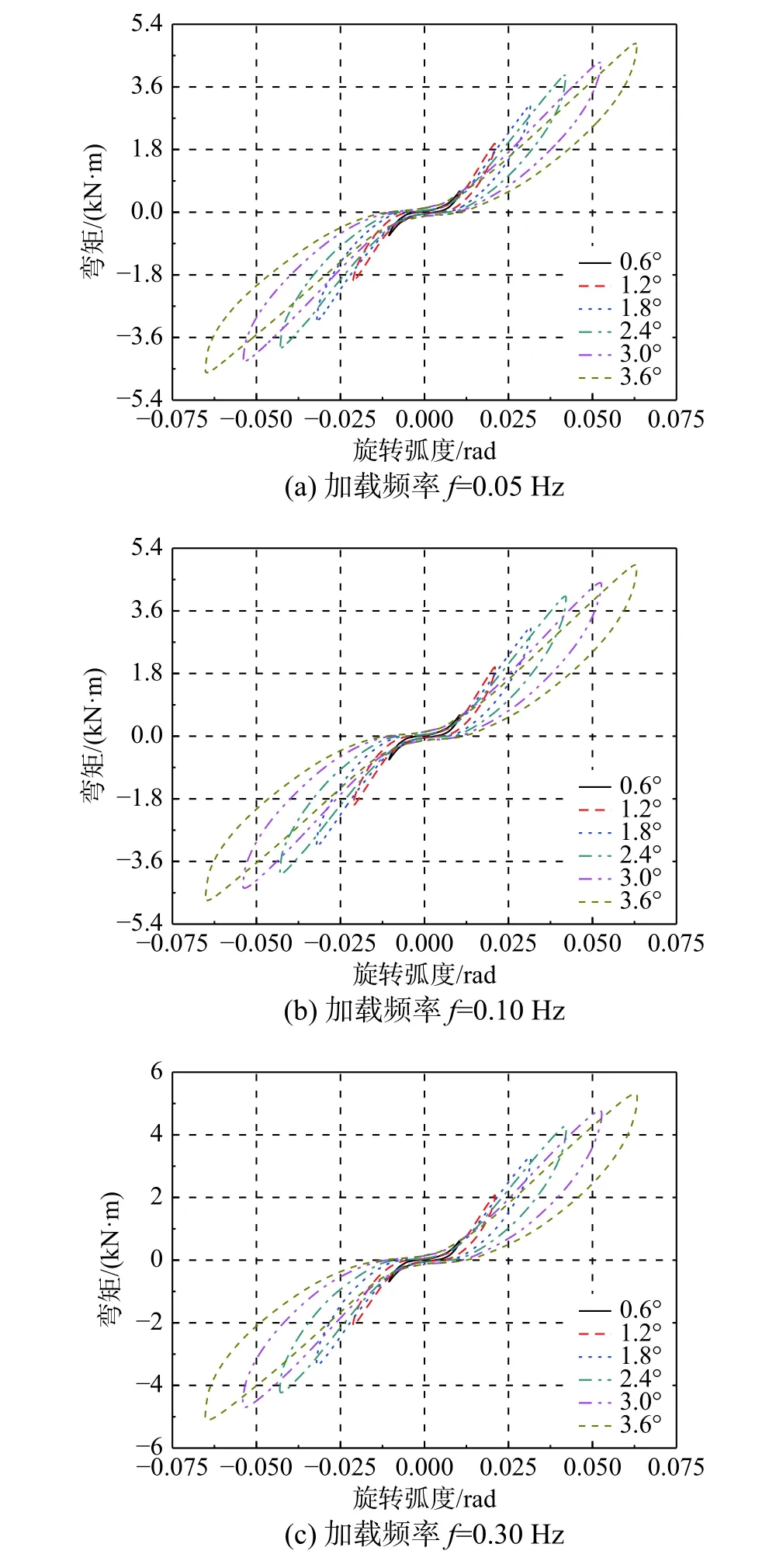
图12 变形相关性试验滞回曲线Fig.12 Hysteretic curve of deformation dependency test

图15给出了该阻尼器各力学性能指标随加载圈数的变化规律曲线。由图15(a)可以看出最大阻尼力P随加载圈数的增加逐渐降低，但降低速度越来越小，前6圈的衰减量与后24圈的衰减量大致相等。由图15(b)可以看出，等效剪切刚度K随加载圈数的增加慢慢退化，由第2圈的98.132 kN·m/rad 下降到第29圈94.102 kN·m/rad，相对衰减率为4.11%。由图15(c)可以看出，每循环耗能ΔW随加载圈数的增加持续降低，但下降速度越来越慢，前10圈ΔW的衰减量占总衰减量的59.51%。由图15(d)可以看出，等效粘滞阻尼比ξ 随加载圈数的增加存在一定的波动性，但总体呈现逐渐降低的趋势。

图13 力学性能指标的变形相关性变化规律曲线Fig.13 Deformation dependency variation law curve of mechanical properties index

表4给出了疲劳性能试验第2圈～第29 圈的各力学性能指标的衰减率，可以发现衡量黏弹性阻尼器疲劳性能的各力学性能指标均呈下降趋势，但衰减率低于《建筑消能阻尼器》(JG/T 209-2012)规范中±15%的规定。因此表明：该阻尼器具有良好的疲劳稳定性，疲劳工况加载对其力学性能和耗能效果影响较小。

4 与传统无放大功能转角阻尼器对比研究

为研究RMVD的实际耗能放大效果，现将阻尼器中起杠杆式放大效果的高强螺杆取出，其他构件尺寸保持不变，重新加工组装成传统无放大功能的黏弹性阻尼器。并按照表2所示的试验加载方案，对其进行相同加载工况下力学性能试验。RMVD和传统无放大功能转角阻尼器对比图如图16所示。

传统无放大功能转角阻尼器试验滞回曲线如图17所示，可以看出所有工况的滞回曲线稳定、饱满。通过对比图12和图17发现该RMVD的滞回曲线在平衡位置附近存在一定的捏缩现象，这是因为在循环加载试验过程中，高强螺杆在圆角矩形滑槽内运动，造成其与扇形旋转剪切板之间存在相对滑移的情况，致使接触传力滞后造成的。

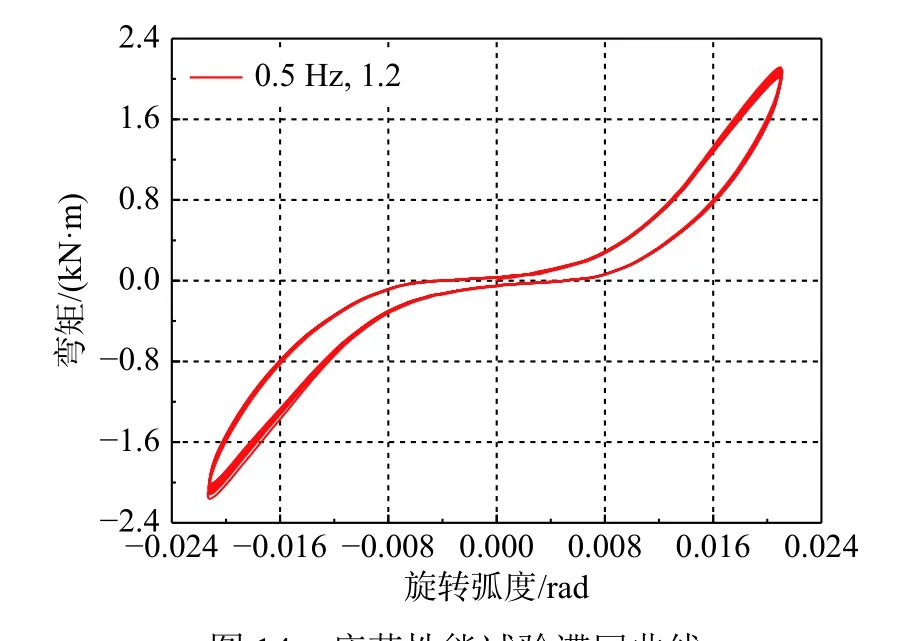
图14 疲劳性能试验滞回曲线Fig.14 Hysteretic curve of fatigue test

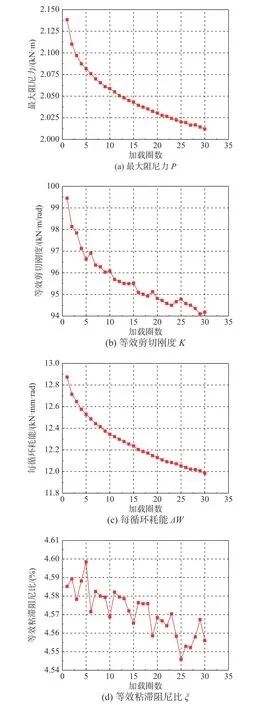
图15 疲劳性能指标试验的力学性能变化规律曲线Fig.15 Variation law curve of mechanical properties index in fatigue test

表4 疲劳性能试验的力学性能指标衰减率Table 4 Decay rate of mechanical properties index in fatiguetest

图16 新型旋转放大式阻尼器和传统无放大功能转角阻尼器对比图Fig.16 Comparison diagram of the RMVD and the traditional angle damper without amplification function

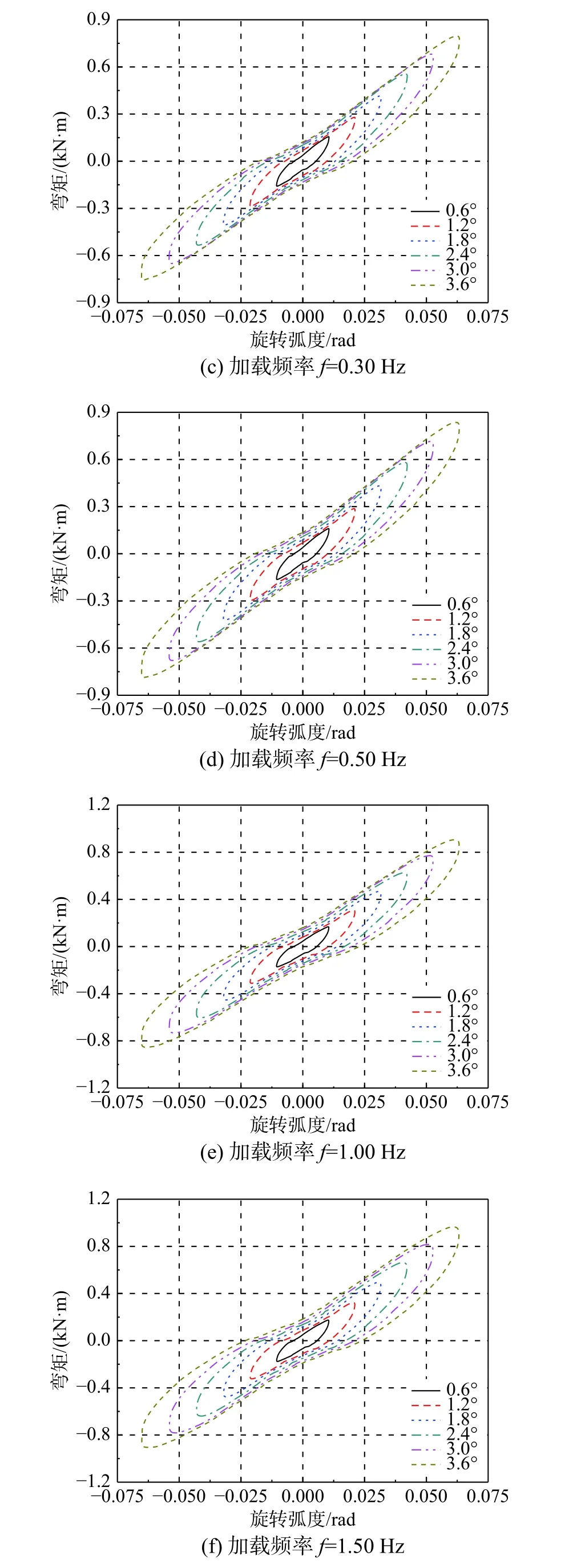
图17 传统无放大功能转角阻尼器试验滞回曲线Fig.17 Hysteretic curve of the traditional angle damper without amplification function

图18 力学性能指标放大倍数的变化规律曲线Fig.18 Variation law curve of mechanical properties index magnification

为进一步对比RMVD与传统无放大功能转角阻尼器耗能效果的差异，图18给出了各力学性能指标放大倍数(RMVD与传统无放大功能转角阻尼器相对应工况下力学性能指标的比值)的变化规律曲线。由图18可知，加载频率对阻尼器各力学性能指标的放大倍数影响较小，旋转角度对其影响较大。由图18(a)、图18(b)可以发现，最大阻尼力P、等效剪切刚度K随加载频率的提高逐渐降低，但下降不明显，最大阻尼力P的放大倍数在3.79～8.51，等效剪切刚度K的放大倍数在3.96～8.58；随着阻尼器旋转角度的增大，最大阻尼力P和等效剪切刚度K的放大倍数均呈先急剧增大后缓慢减小的趋势。由图18(c)可以发现，每循环耗能ΔW的放大倍数均大于1，其随加载频率的提高波动性较小；每循环耗能ΔW的放大倍数随着阻尼器旋转角度的增大持续增大，但增大速度逐渐降低，当加载角度为3.6°、加载频率为0.5 Hz时，ΔW的放大倍数达到最大值4.42。

综上所述：与传统无放大功能转角阻尼器相比，该RMVD的耗能放大效果显著，能在结构发生小变形的情况下充分发挥阻尼器中黏弹性材料的滞回变形耗能能力，达到更理想的耗能效果。

5 结论

本文设计制作了一种新型旋转放大式黏弹性阻尼器，通过不同工况下的循环加载试验，研究了其各项力学性能指标随加载频率和转角变形幅值的变化规律以及抗疲劳能力。并与传统无放大功能转角阻尼器进行了相同加载工况下的耗能对比，验证了该阻尼器的耗能放大效果。具体结论如下：

(1)该新型旋转放大式黏弹性阻尼器的滞回曲线饱满，滞回性能稳定，表现出良好的耗能能力。

(2)随加载频率的提高，滞回曲线越发饱满，耗能能力持续增强。最大阻尼力、等效剪切刚度、每循环耗能、等效粘滞阻尼比随加载频率的提高均逐渐增大，但增长率逐渐减小，每循环耗能最大增幅达93.54%。

(3)随转角变形幅值的增加，最大阻尼力、每循环耗能逐渐增大；等效剪切刚度先增大后减小，当阻尼器旋转角度为1.8°时达到最大值；等效粘滞阻尼比先减小后增大，当旋转角度为1.2°时达到最小值。

(4)疲劳试验加载中滞回曲线形状基本保持不变，各力学性能指标衰减率均小于5.51%，满足规范的要求[15]。

(5)该旋转放大式黏弹性阻尼器耗能放大效果显著。随阻尼器旋转角度的增大，最大阻尼力和等效剪切刚度的放大倍数呈先增大后减小的趋势，最大放大倍数均达到8.5倍；每循环耗能的放大倍数持续增大，放大倍数最大值为4.42。