一种基于头架主轴为变速运动的曲轴随动磨削加工方法研究*

范晋伟 李晨宝 李伟华 谢本田

(①北京工业大学材料与制造学部，北京 100022；②北京第二机床厂有限公司，北京 100165)

在曲轴随动磨削加工过程中，磨削运动轨迹直接影响加工精度和效率[1]。针对曲轴随动磨削方式较为复杂的特点，本文提出一种基于头架主轴在旋转过程中为变速运动，工件磨削点相对于连杆颈中心为恒速运动的曲轴随动磨削方法，并分别对主轴变速随动磨削运动轨控制模型和传统控制模型[2]进行仿真分析。

1 随动磨削加工瞬时位置方程的建立

为满足曲轴高效、精密加工要求，曲轴的磨削技术朝着数控非圆磨削方向发展。所谓非圆磨削一般是指在数控磨削过程中，磨削点的轨迹为非圆曲线的磨削过程[3](其工作原理如图 1 所示)，是通过控制曲轴的回转运动(C轴和砂轮的直线进给运动X轴)，保持砂轮外圆与曲轴连杆颈加工表面始终处于相切的状态，从而保证曲轴的轮廓精度[4]。如图2所示，在加工连杆颈的过程中，通过控制头架的回转运动与砂轮的横向的进给，来确保砂轮的磨削点始终与连杆颈相切，达到实时跟踪磨削。

图 3 为在曲轴随动磨削过程中在某一瞬时的砂轮与曲轴的相对位置关系。首先，在主轴颈轴、砂轮以及连杆颈轴中心建立与各自部件固连的坐标系O1X1Y1，O2X2Y2，O3X3Y3。其次，在主轴颈轴中心建立固定惯性坐标系O0X0Y0。初始位置时，主轴颈转角θ1与连杆颈转角θ2为零。其他坐标系坐标轴均与惯性坐标系平行，令坐标系O1X1Y1原点坐标为(0，0)，则坐标系O2X2Y2的原点坐标表示为(LSC，0)，坐标系O3X3Y3的原点坐标为(Re，0)，设砂轮位移量参数为x。

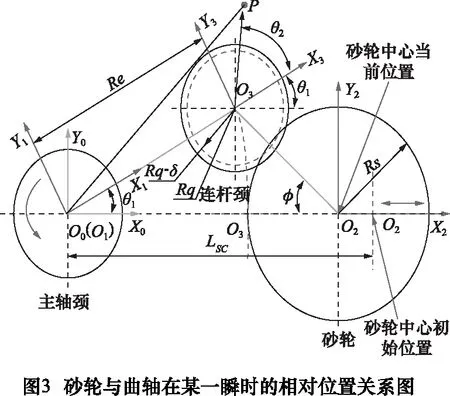
设在坐标系O3X3Y3中有一矢量O3P，起点为(0，0)，终点为任意点P，与X3轴的夹角为θ2，任意点P在坐标系O3X3Y3中的坐标表示为：

(1)

由坐标变换原理可得任意点P在坐标系O1X1Y1中的坐标为：

(2)

当主轴颈做回转运动时，任意点P在惯性坐标系中的坐标为：

(3)

式中：Re为主轴颈与连杆颈的中心距；θ1为曲轴绕主轴颈中心转动的角度。

在惯性坐标系中令任意点P与砂轮中心相重合，得到随动磨削加工过程中任意点P的瞬时位置方程：

(4)

式中：r连杆颈和砂轮中心距，为Rq+Rs-δ；Rq为连杆颈半径；Rs为砂轮半径；δ为磨削余量；LSC为初始位置时主轴颈与砂轮轴中心距；x为砂轮横向进给时位移量。

由式(4)第二行可得：

Resinθ1+rsin(θ1+θ2)=0

(5)

对式 (5) 求一阶导，从而得到：

Recosθ1ω1+rcos(θ1+θ2)(ω1+ω2)=0

(6)

在坐标系O3X3Y3中，砂轮绕连杆颈轴中心转速为：

(7)

式中：ω1为主轴颈转速；ω2为砂轮绕连杆颈轴中心转速。

由式(7)可得，为避免产生速度位置奇异，则θ1+θ2≠90°， 根据式(5)可得：

(8)

其中r为Rq+Rs-δ，得随动磨削约束方程：

Rs>|Resinθ1-Rq+δ|

(9)

所以砂轮半径应取较大，而实际生产加工中，砂轮半径远大于该值。

2 随动磨削运动轨迹控制模型的建立

曲轴随动磨削加工实质是数控系统按照一系列关于θ1-x的离散数据点指令来驱动砂轮磨削点与连杆颈任意加工点始终处于相切的状态，其中θ1表示主轴转动角度，x表示砂轮平移运动的位移。为了避免连杆颈表面的加工问题，本文采取恒磨除量的磨削方式。

将砂轮绕连杆颈轴中心旋转一周范围内θ2值进行离散化，以Δθ为均匀采样周期，如下式：

(10)

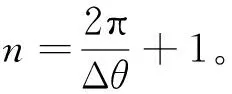
由式(4)第二行可得：

(11)

利用式(11)，得到相应的θ1的离散值，然后根据式(4)第一行得到对应的x值，即数控系统发出驱动指令信息，从而得到数据矩阵列表：

(12)

利用式(12)，根据θ2-θ1-x离散矩阵列表，获得曲轴随动磨削控制参数，从而建立了随动磨削运动轨迹控制模型。由式(4)第二行可知，θ1的值存在多组解的情况，因此在实际的加工过程中，给定曲轴连杆颈中心在砂轮坐标系中的坐标(xO3O2,yO3O2,zO3O2)T，根据图 3 中砂轮与曲轴在某一瞬时的相对位置关系，在惯性坐标系中令任意点P与砂轮中心重合，可以得到式(11)和(12)，从而得到θ1的值。

θ1=θ2-φ

(13)

(14)

将式(14)整理成如下形式：

(15)

当θ2=0时，φ=0，θ1=0；

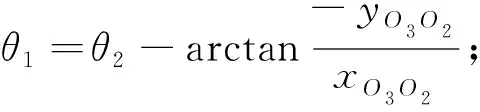
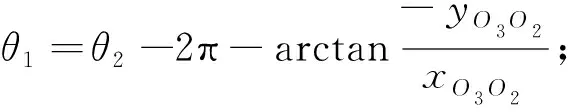
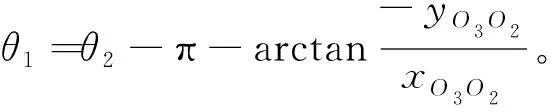
3 建模仿真分析

为验证本文所提出的主轴变速磨削运动轨迹控制模型具有可行性，本节分别对主轴变速磨削运动轨迹控制模型和传统控制模型两种方法进行了仿真分析，并对分析结果进行了量化。

在给定连杆颈轴半径与磨削余量下，选择砂轮半径分别为 200 mm、400 mm和800 mm进行仿真。根据式(7)和式(13)，保持主轴转速ω1为π/3不变，得到传统磨削方式转速影响曲线图，r如图4所示。根据转速影响曲线图得到转速差值柱状图和转速差值降幅率，分别如图6和表1所示。保持砂轮绕连杆颈中心转速ω2为π/3不变，可以得到主轴变速磨削方式的转速影响曲线图，从而得到转速差值柱状图和转速差值降幅率，如图4、图6和表11所示。

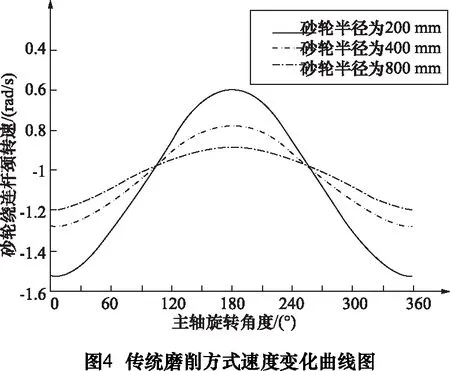
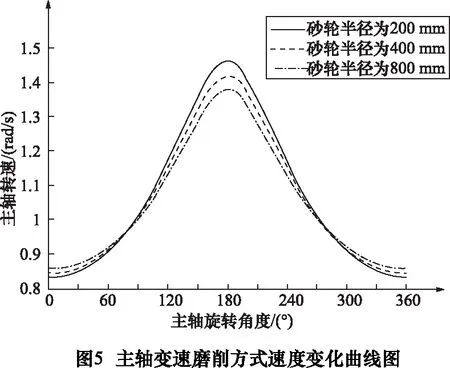
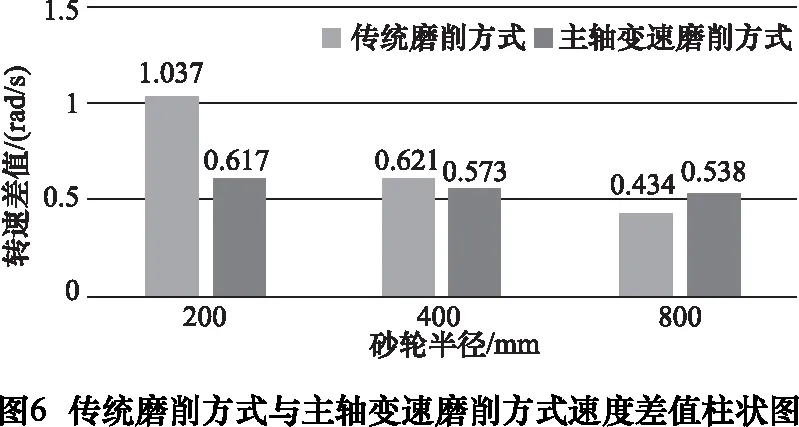
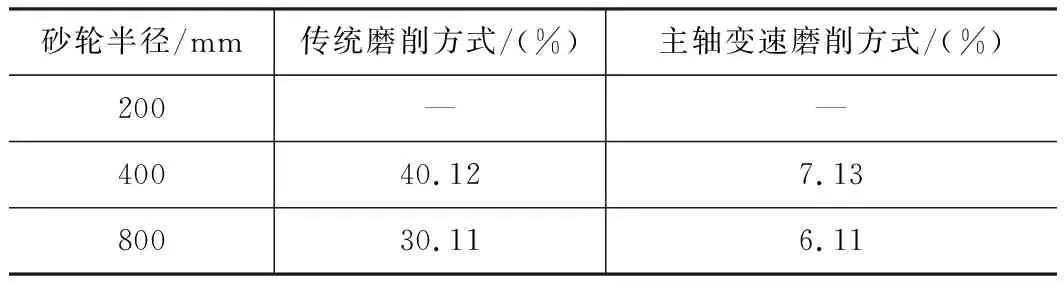
表1 转速差值的降幅率

根据图4和表1，随着砂轮半径的增大，传统磨削方式的转速差值，分别为1.037 rad/s、0.621 rad/s和0.434 rad/s，转速差值降幅率分别为40.12 %和30.11 %；而本文提出的主轴变速磨削方式的转速差值分别为0.617 rad/s、0.573 rad/s和0.538 rad/s，转速差值降幅率分别为7.13%和6.11%。由此可见，本文提出的磨削方式受砂轮尺寸的影响较小。因此，本节提到的随动磨削运动轨迹控制模型，转速和受力状态相对稳定，能大大提高曲轴的表面加工质量。

4 结语

本文提出的一种基于头架主轴在旋转过程中为变速运动的恒磨除率曲轴随动磨削方法。针对曲轴随动磨削加工的运动结构和工作特点，推导出磨削加工时，砂轮和曲轴磨削点的瞬时位置运动轨迹表达方程。利用一系列关于θ2-θ1-x的离散数据矩阵列表，获得头架旋转的控制参数和砂轮驱动位置信息，从而建立了曲轴随动磨削运动轨迹控制模型，为达到恒速曲轴随动精密磨削加工奠定了理论基础。最后利用仿真分析对比传统磨削方式与本文提出的主轴变速随动磨削方式，观察到本文提出的主轴变速磨削方式受砂轮尺寸影响较小，连杆颈上的磨削点相对于转动中心的速度和受力状态是相对稳定的，能大大提高曲轴的表面加工质量。