一类具有等级结构的种群系统的最优控制
徐 阳,赵 春
(天津师范大学数学科学学院,天津300387)
研究不同生物种群的特性,对帮助人们在合理利用自然资源的基础上达到与自然和谐共生的状态有非常重要的意义.大部分种群系统中存在等级差异[1],具有等级差异的种群模型也能更准确地反映现实情况,等级结构差异包括年龄、尺度和攻击力等因素.近年来,关于具有年龄结构与尺度结构的种群模型已取得了一些研究成果[2-11].其中:文献[9-10]研究了一类由“年长优先”原则所确立的等级结构种群模型,分析了模型的适定性和预设目标调控问题;文献[11]分析了一类年轻个体占优的生物种群模型解的适定性,利用特征线法和不动点原理得到了非负解的存在唯一性和有界性,以及解对控制变量的一致连续性.本文研究一类年长个体占优的种群系统的最优控制问题,证明了系统解的存在唯一性和解对控制变量的连续依赖性,利用法锥的性质得到了最优控制的必要性条件.
1 模型建立
考虑如下模型
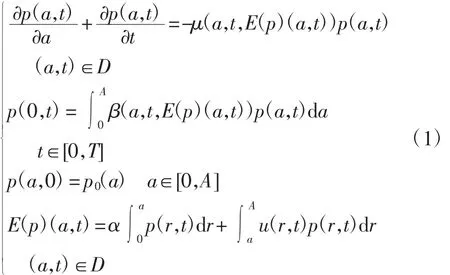
其中:D=[0,A]×[0,T],A 为种群个体的最大年龄,T为种群个体的控制周期;年龄为a 的个体被赋予较小权重值 α,0≤α <1;p(a,t)为t 时刻年龄为a 的种群密度;μ 和β 分别为个体的平均死亡率和繁殖率,均与环境E(p)有关;p0(a)为种群个体年龄的初始分布;u(a,t)为控制变量,满足u∈X={v(a,t)∈L∞(D),0≤
本文做如下基本假设:
(H1) μ(a,t,x)≥0,β(a,t,x)≥0 (a,t,x)∈D×R+
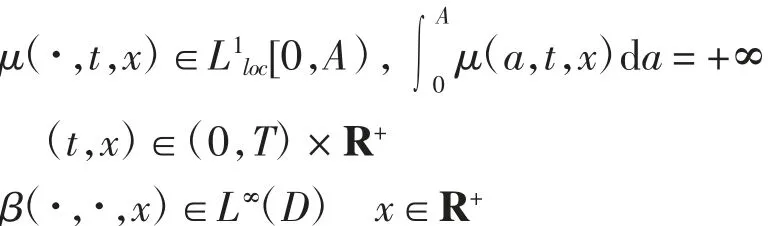
(H2) μ 和 β 关于第3 个变量均满足Lipschitz 条件:对任意M >0,存在常数L(M)>0,使得
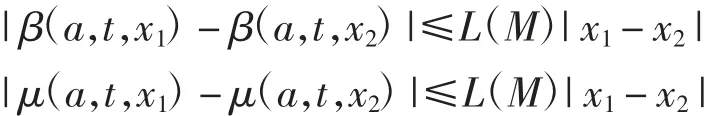
对满足|xi|≤M,i=1、2 的x1、x2均成立.
(H3)对任意给定的(a,t)∈D,β(a,t,·)单调不增,μ(a,t,·)单调不减.
(H4)p0(a)∈L∞(0,A),0≤p0(a)≤p0,p0为正常数.
考虑控制问题
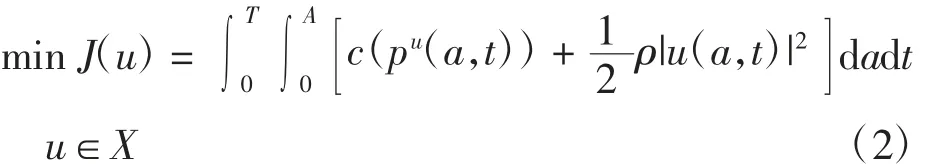
其中:pu(a,t)为状态系统(1)对应于u(a,t)的解;ρ >0表示控制成本因子;对任意x∈R+,有c(x)∈C2(R+),c(x)≥0,c′、c″均有界.
定义 若p(a,t)∈L∞(0,T;L1(0,A))在每条特征线t-a=k 上都绝对连续,k 为常数,且
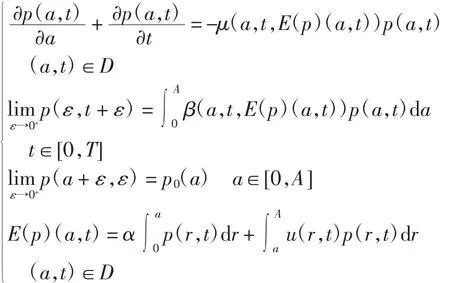
则称p(a,t)为系统(1)的解.
2 解的存在唯一性
取固定函数q(a,t)∈L∞(0,T;L1(0,A)),q(a,t)≥0,考虑系统
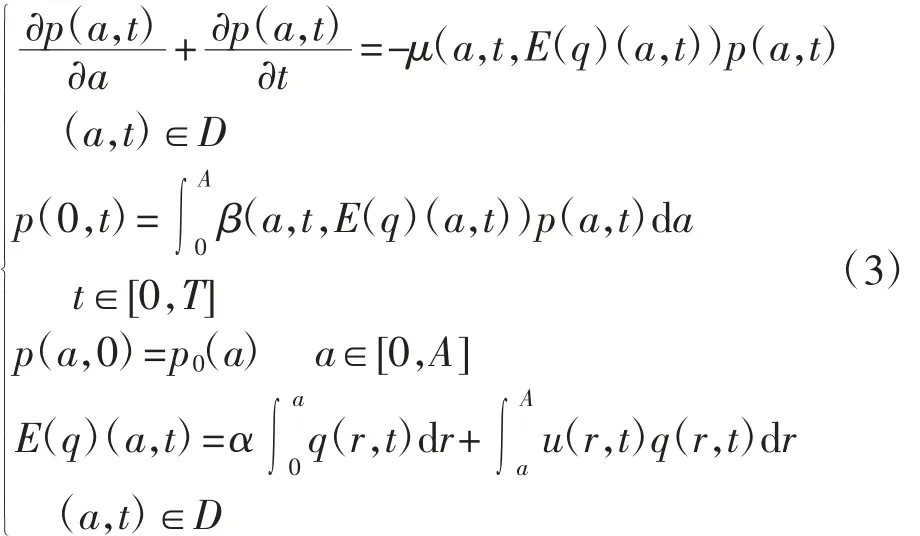
由文献[12]知系统(3)必有唯一非负解
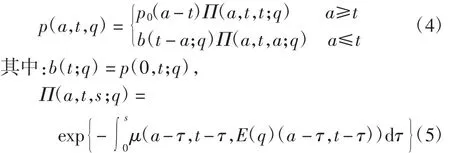
将式(4)代入系统(3)的第2 个等式,可得b(t;q)满足
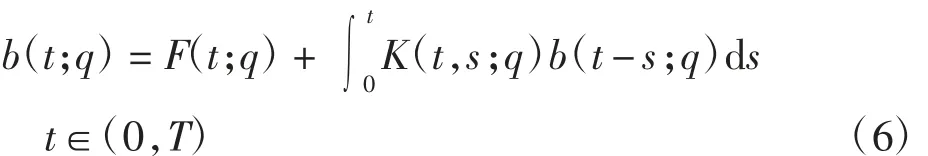
其中:
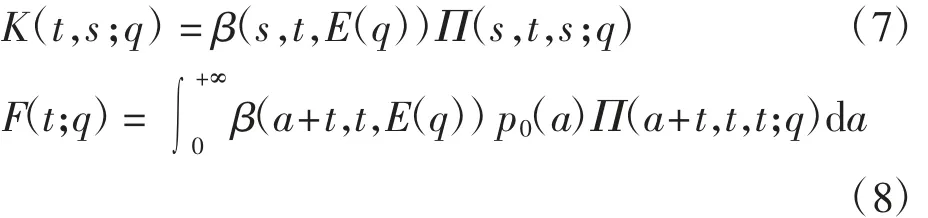
式(7)和式(8)中的函数β 和p0在其定义域外延拓为0.
下面的讨论在T >A 的情况下进行,对于T≤A的情况,讨论过程类似且更简单.
定义
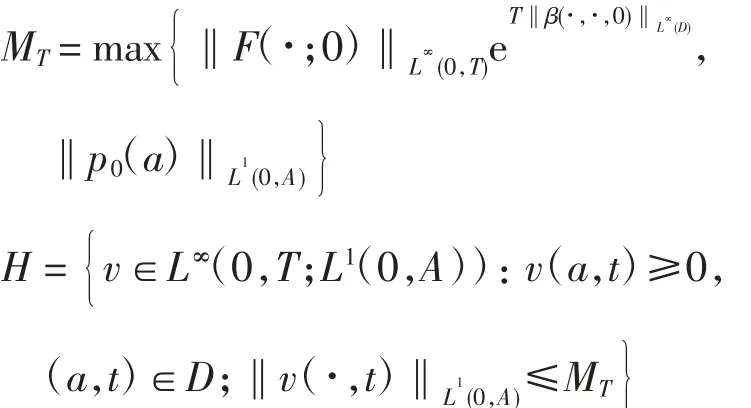
引理1 存在常数M1T、M2T≥0,使得对任意q1、
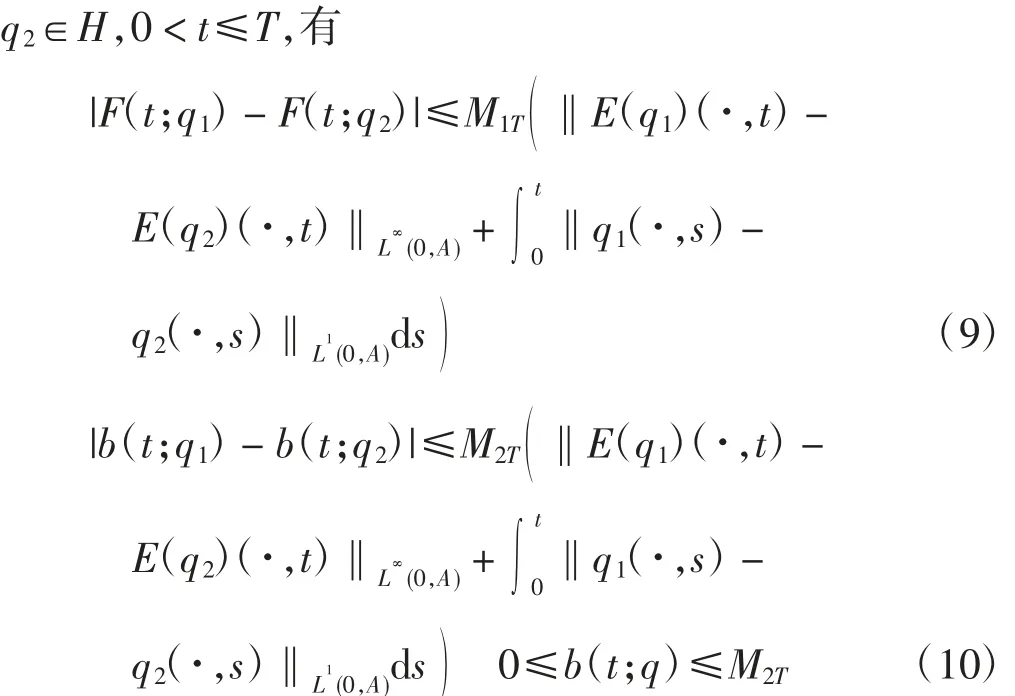
证明当t∈[A,T]时,β(a + t,t,E(q))≡0,则F(t;q)≡0,显然式(9)成立.
当t∈(0,A)时,由系统(3)的第4 个等式有
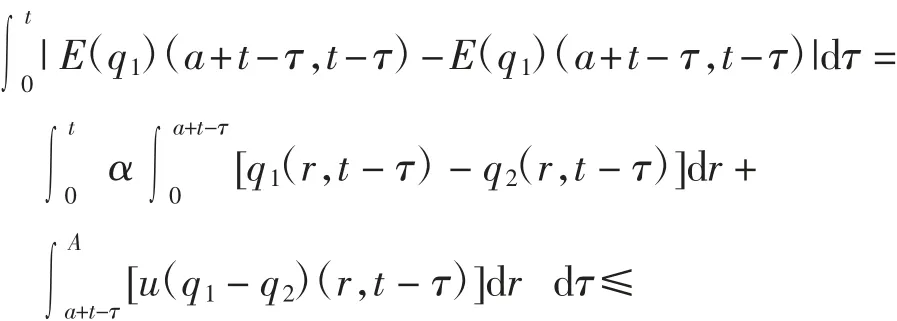
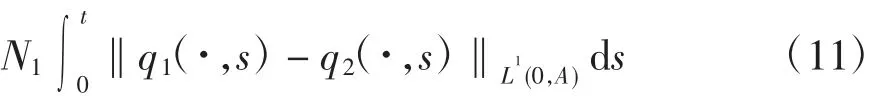
其中N1=max{1,u}.
利用式(5)和式(8)可得
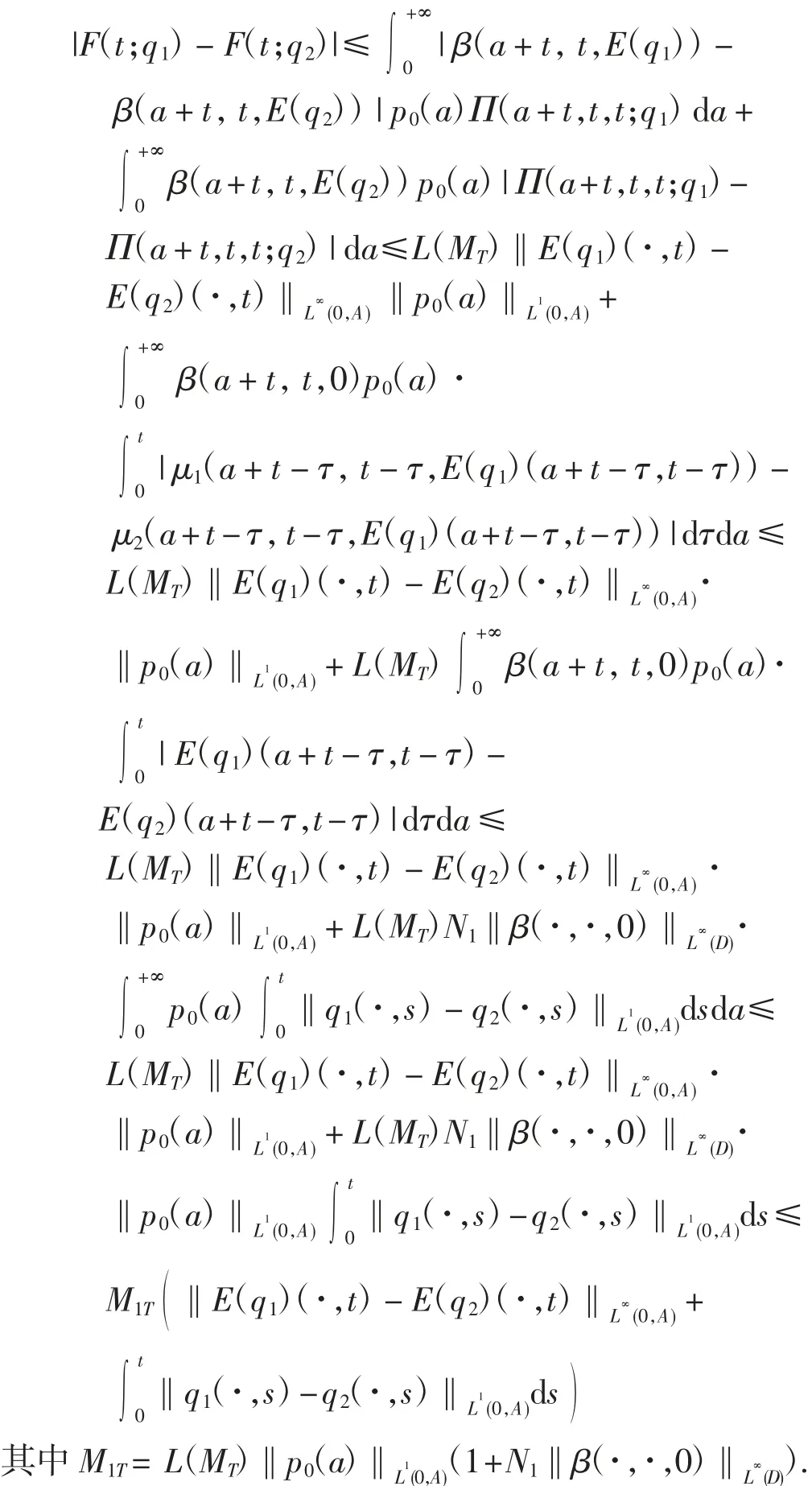
因此式(9)成立.
利用式(6)和Bellman 引理可得
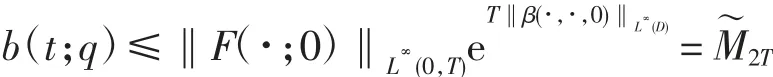
由基本假设及式(6)~式(8)可得
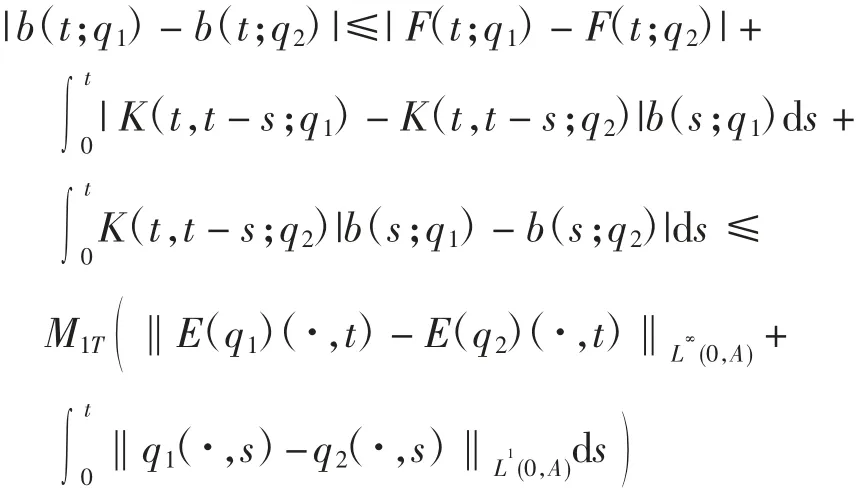
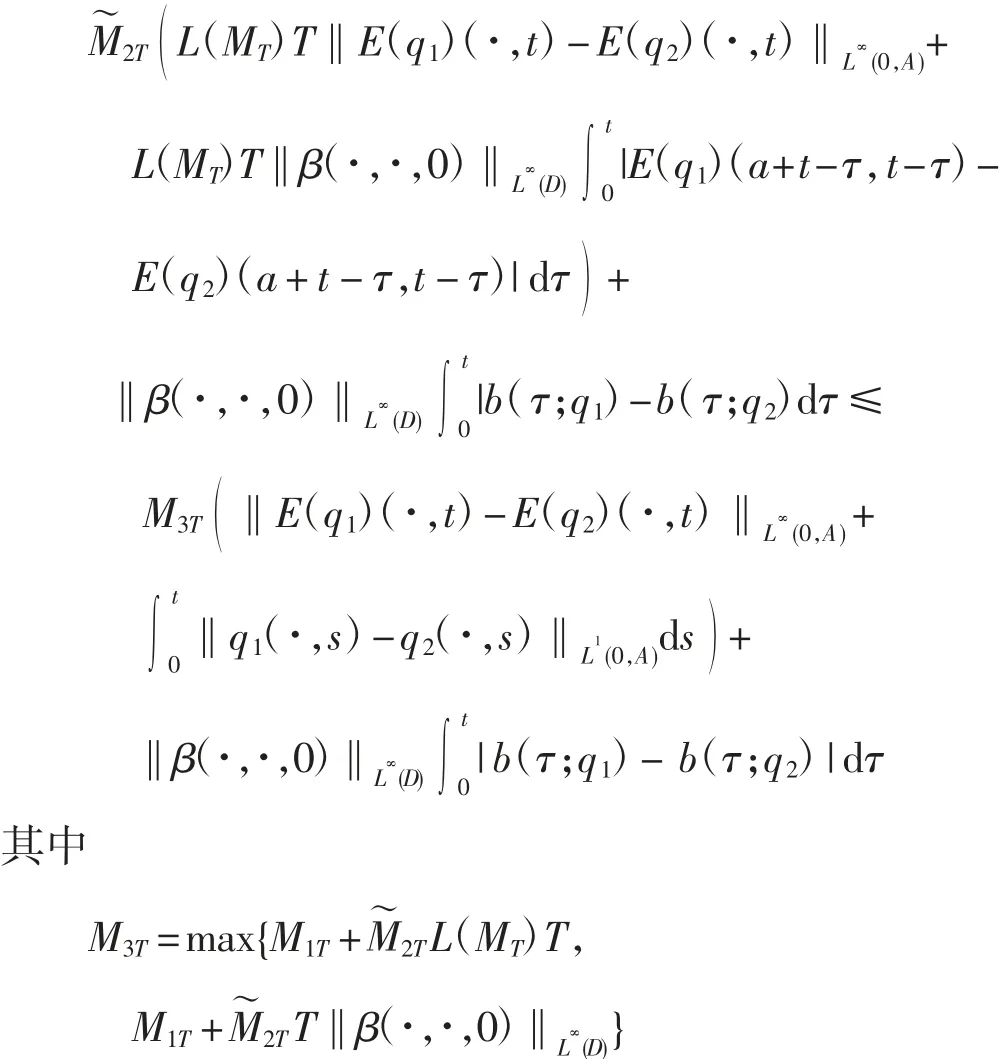
再由Gronwall 引理可得式(10)成立.引理证毕.
定义映射
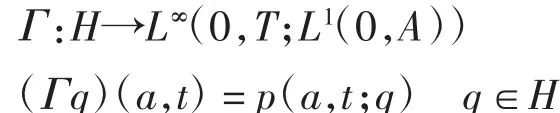
其中p(a,t;q)为系统(3)的解.
引理2 映射Γ 是一个从H 到其自身的映射,且存在仅依赖于T 的常数MT>0,使得对任意q1、q2∈H,0 <t≤T,有
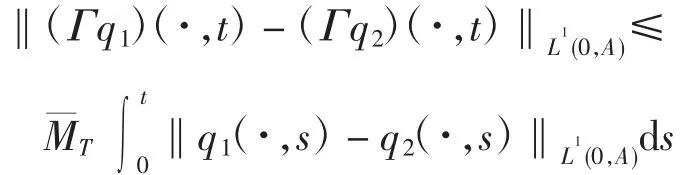
证明当t∈(0,A)时,利用式(4)和引理1 可得
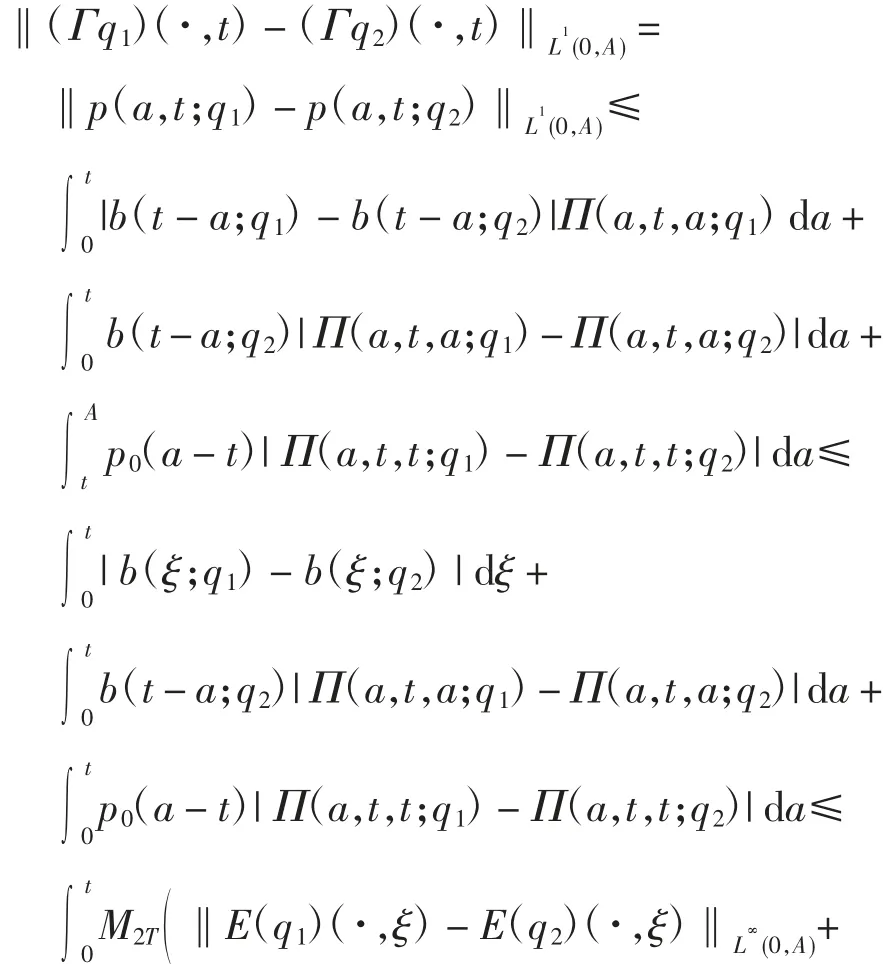
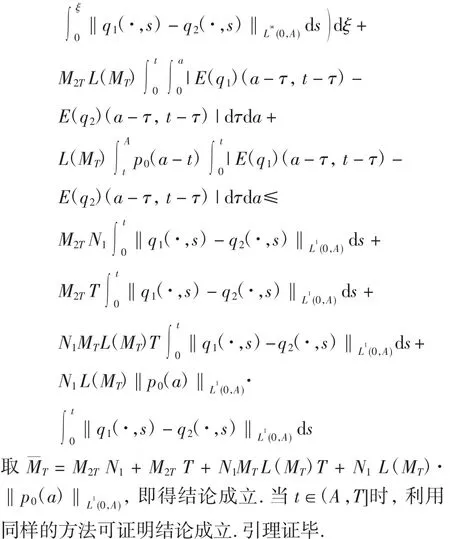
定理1 设条件(H1)~(H4)成立,则系统(1)有唯一非负解.
证明选择常数λ >MT,定义L∞(0,T;L1(0,A))上的等价范数为
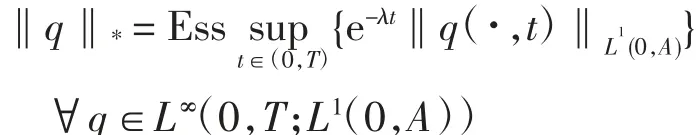
由引理2 可得
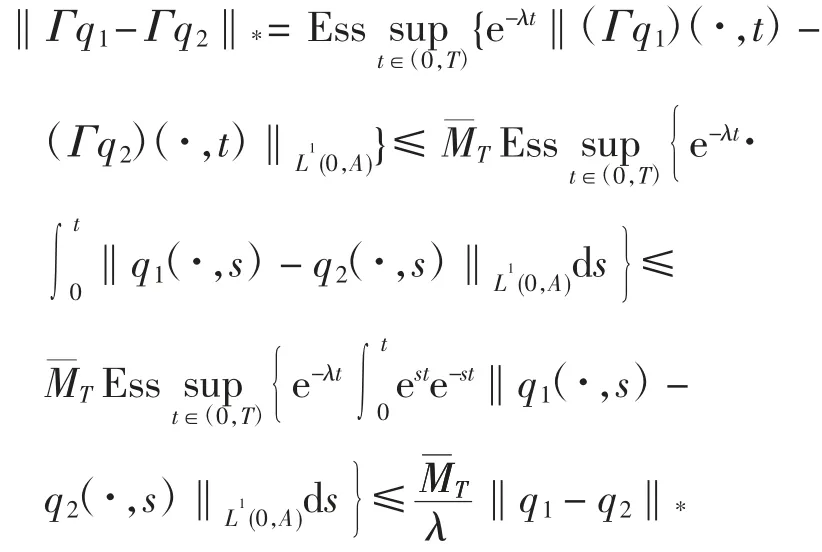
因此Γ 为一个压缩映射,由Banach 不动点定理知,映射 Γ 具有唯一的不动点q*,q*即为系统(1)的解.定理证毕.
3 解对控制变量的连续依赖性
仅讨论T >A 的情况,T≤A 的情况讨论过程类似.
利用特征线法,系统(1)的解可表示为
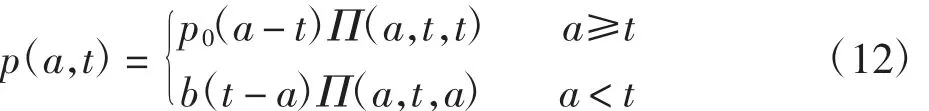
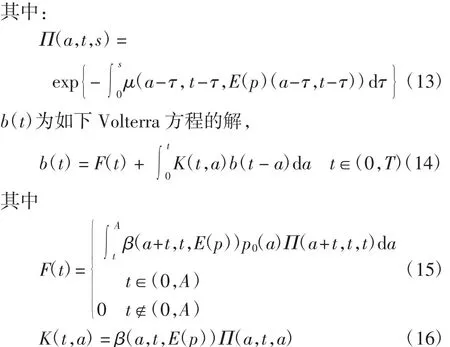
引理3 对任意u、v∈X,存在不依赖于u、v 的常数C1、C2,使得
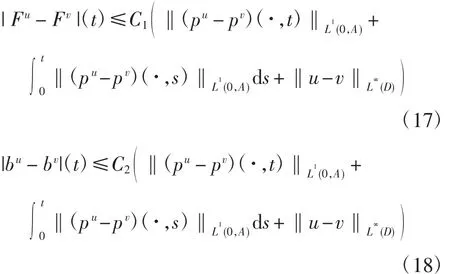
证明当t∈(A,T)时,β≡0,则F(t)≡0,显然式(17)成立.
利用系统(1)与式(13)可得
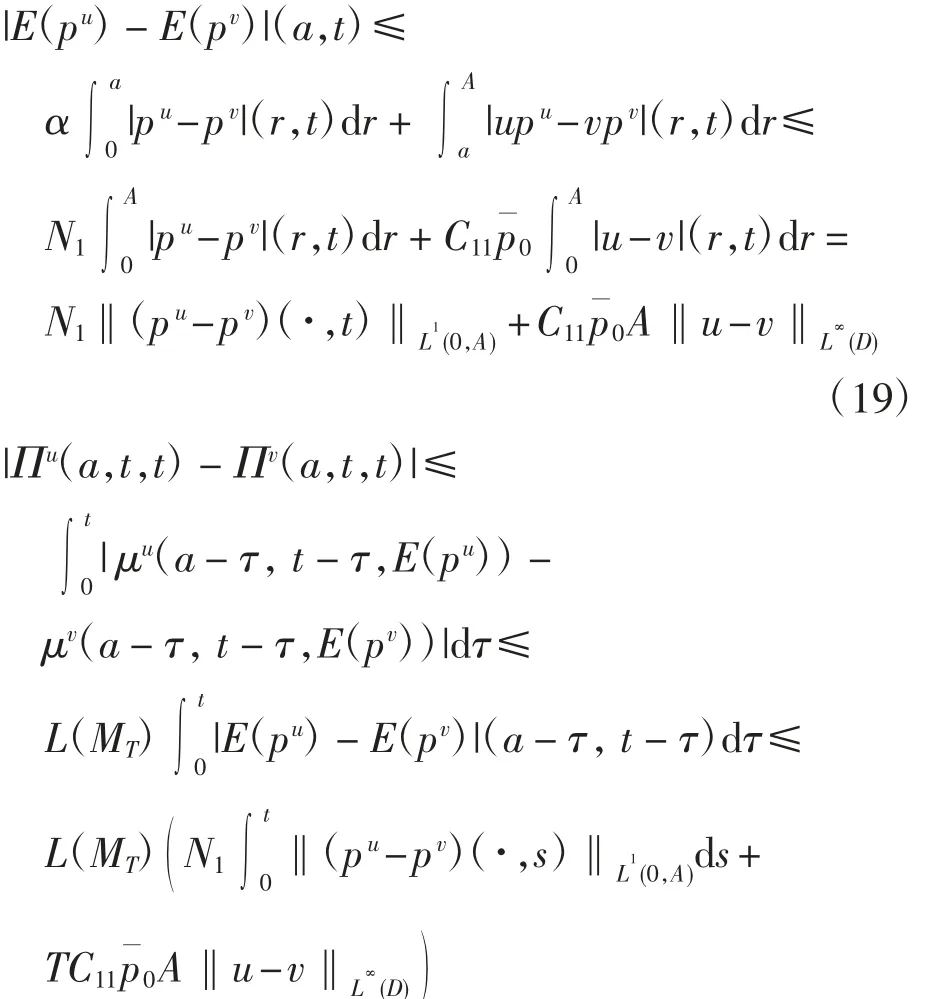
当t∈(0,A)时,由式(13)、式(15)和条件(H1)~(H4)可得
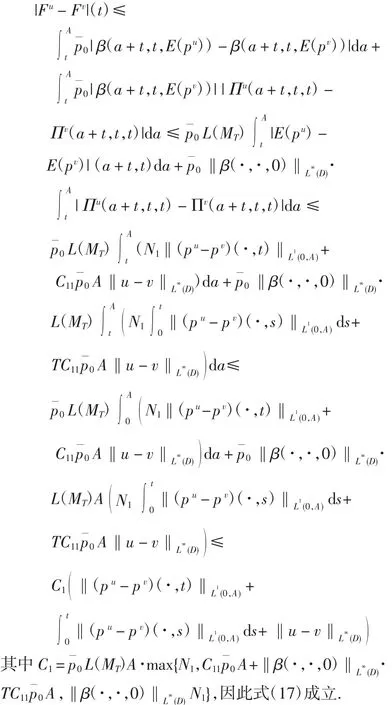
由式(14)~式(16)可得
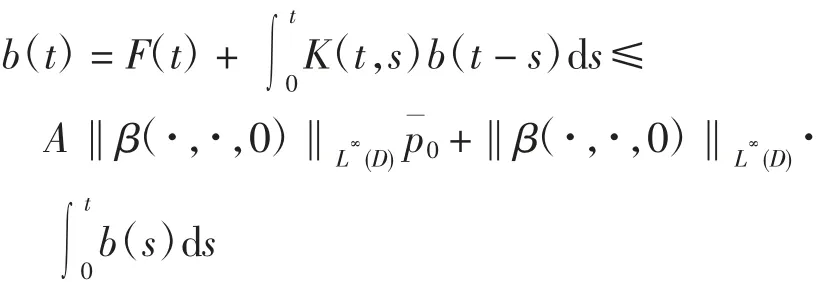
再利用Bellman 引理可得
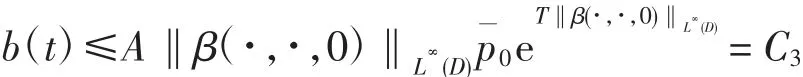
由式(13)和式(16)可得
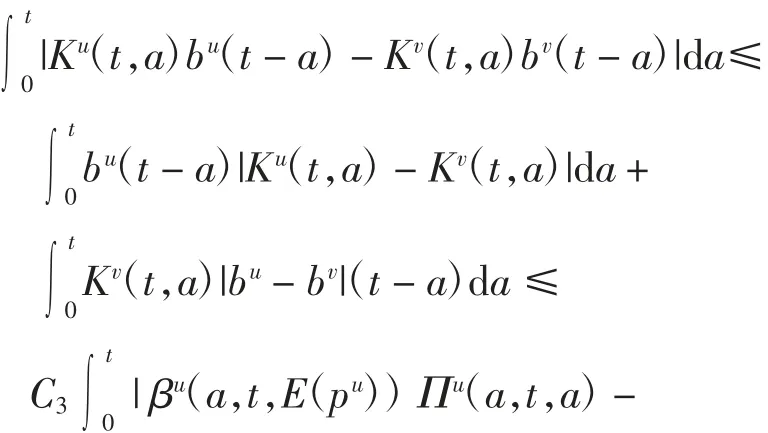
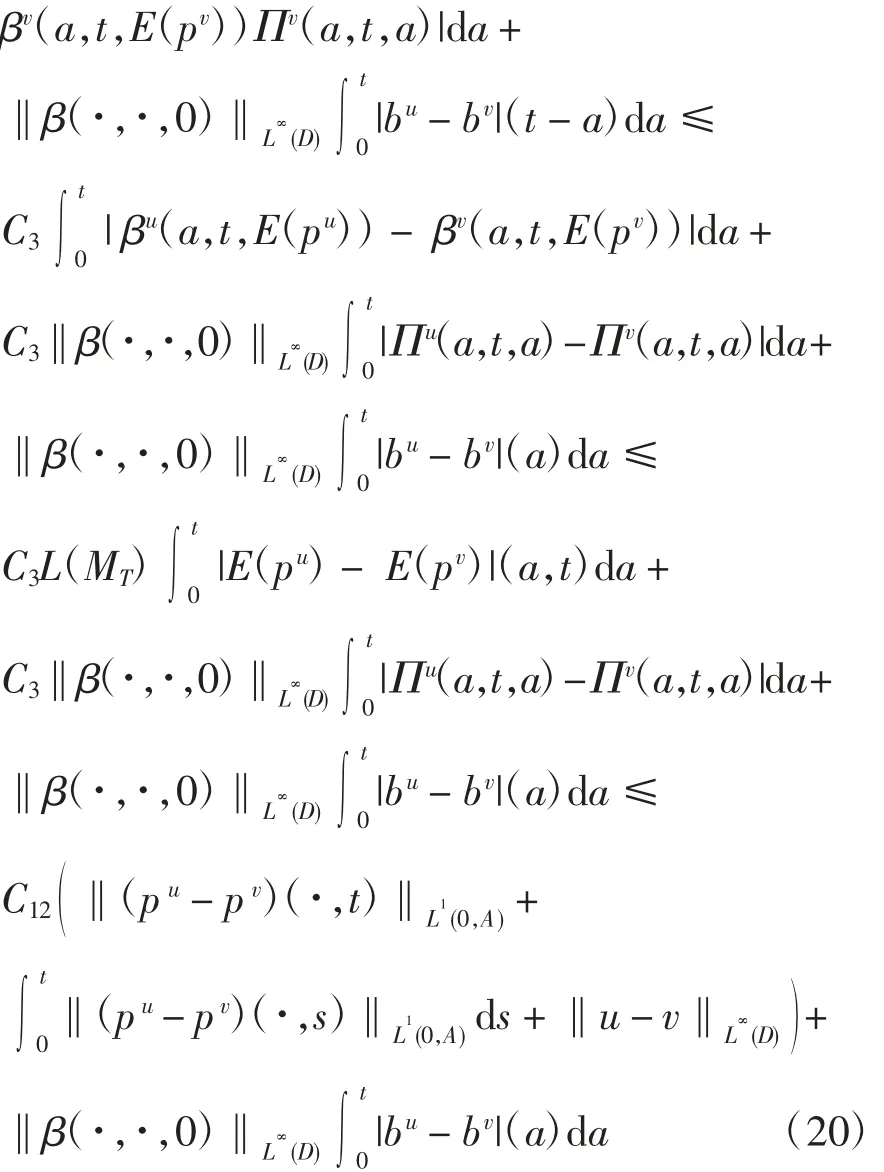
其中C12是与u、v 无关的常数.由式(14)、式(17)和式(20)可得

证明由式(12)、式(18)和式(19)可得
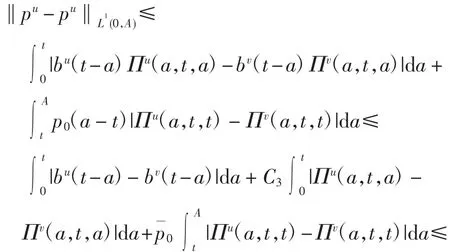

定理证毕.
4 最优控制的必要性条件
定理3 设(u*,p*)为系统(1)的最优解,q*满足如下共轭系统
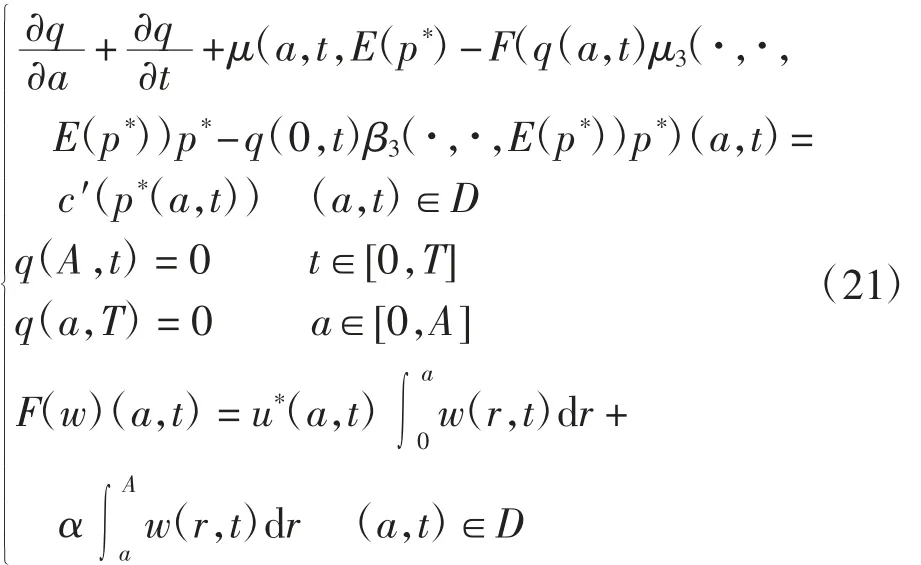
其中 μ3和 β3分别为 μ 和 β 对其第3 个变量的偏导数.最优控制可表示为
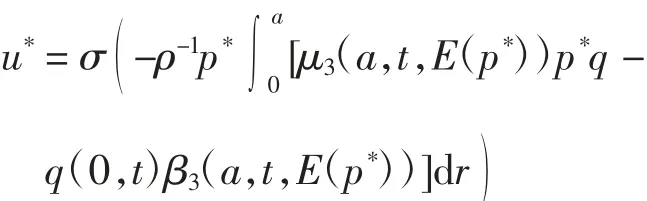
其中函数σ 定义为
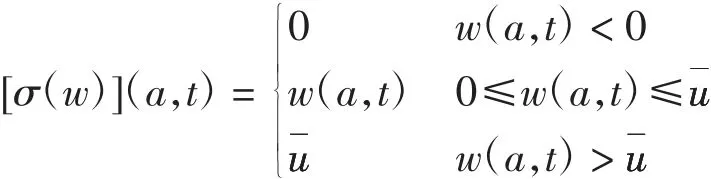
证明对任意v∈T(Xu*)(容许控制集X 在u*处的切锥),当 ε >0 且充分小时,有uε=u*+εv∈X.由J(u*)≤J(uε)得
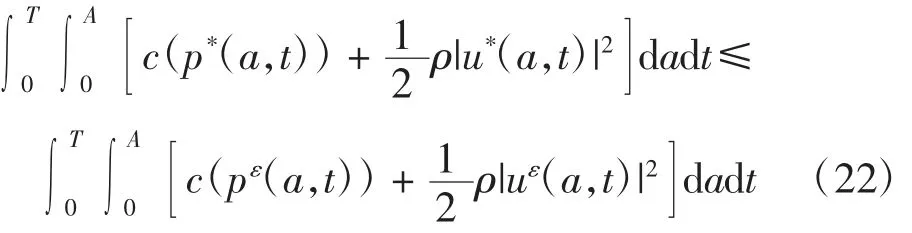
其中pε是系统(1)及其控制问题(2)相应于uε的解.由式(22)可得
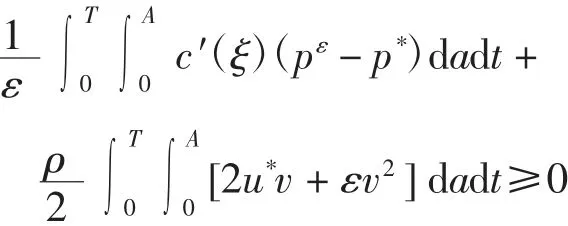
其中 ξ 是介于p*与pε之间的一个函数.令 ε→0+,可得

将方程(24)的第1 个式子两边同时乘以q(a,t),加上系统(21)的第1 个式子两边同时乘以z(a,t),并在D上积分,得到
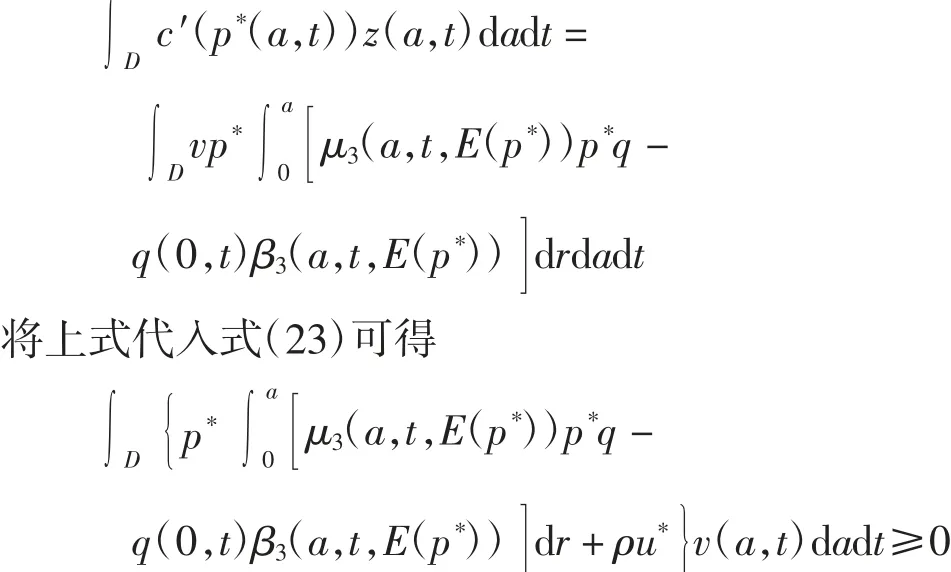
根据法锥的定义可得
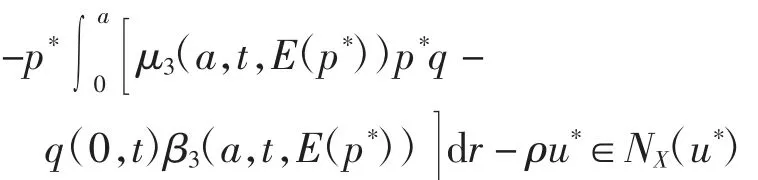
由法锥的性质可知结论成立.定理证毕.

