基于统一边界和梁格模型的整体式桥台桥梁分析

金永学，徐 栋，郑明万，贾 栋

（1.同济大学土木工程学院，上海200092；2.济南市市政工程设计研究院（集团）有限责任公司，山东济南250002）

桥梁伸缩缝有着释放温度变化产生的纵向变形和汽车荷载产生的纵向变形及梁端转动变形的作用［1］。然而，伸缩缝直接承受车轮荷载的反复冲击且易因灰土杂物的堵塞而失去作用。其作为桥梁的薄弱部位病害多发、耐久性差，需要进行长期的维护和更换［2］。由此设想，对于一些中小跨径的桥梁，可以取消桥梁的伸缩缝将梁与桥台连成一体。这样的桥梁被称为整体式桥台桥梁。

由于整体式桥台桥梁的上部结构与下部结构连成一体，在计算时需要同时建立上、下部结构模型并考虑结构-土相互作用。针对结构模型问题，Diclei［3-4］提出一种简化的二维框架模型，桥台桩基础及桩侧土作用通过一定长度的悬臂梁等效，而Faraji等［5］提出了三维弹簧-框架的有限元模型，采用离散的文克勒土弹簧作为桥梁结构的边界条件，三维模型能够计算出桥梁受力的空间效应，且相较于等代悬臂梁法，土弹簧对土体进行模拟更为准确，故三维弹簧-框架的计算模型目前更为人们所接受；针对结构-土相互作用问题，根据弹性地基梁理论，一般认为桩上任一点所受的横向弹性土抗力与该点的位移成正比，且不考虑桩土之间的粘着力和摩阻力，即

式中：σxz为深度z处桩的弹性土抗力；Cz为深度z处的地基系数，表示单位面积土在弹性限度内产生单位变形时所需的力；Xz为深度z处桩的横向位移。

地基系数与土体类别、性质有关，且随深度变化而变化。常用的几种确定地基系数的方法有：“m”法、“K”法、“c值”法和“C”法［6］。由于测试条件和分析方法的不同，几种方法描述的地基系数随深度的分布规律也有所差异。我国的《公路桥涵地基与基础设计规范》JTG D63—2007［7］提供的确定地基系数的方法是“m”法，认为地基系数Cz值随深度成正比例地增长，即

式中：m为地基比例系数；z为地基土深度。

湖南大学邵旭东、马竞、刘钊等［8-9］在清远市四九桥的模型中将“m”法确定刚度的文克勒弹簧作为整个结构的边界条件，进行整体式桥台桥梁的力学性能分析。

结构-土相互作用可以从台-土相互作用和桩-土相互作用2个部分讨论，二者的不同之处在于桥台单侧与土体相互作用，桩两侧均与土体相互作用。在只考虑土体受压性能的条件下，对桩单侧布置土弹簧作为边界条件模拟桩-土相互作用是合理的；而台后沿高度方向何处需要布置土弹簧应根据具体工况具体分析：在某一给定工况下，结构与土体挤压的位置应布置土弹簧，结构与土体脱开的位置应撤掉土弹簧，因此在计算过程中需要对结构体系进行反复调整。这种边界条件非线性造成体系与荷载相关，给实桥的设计带来诸多困难。我国的《公路桥涵设计通用规范》JTG D60—2015［10］给出多种组合对桥涵进行设计，每种组合下各项荷载又要考虑分项系数。对于整体式桥台桥梁，具体分项系数下的荷载组合带来较大的工作量，不利于设计与调整。

本文选取一座两跨的整体式桥台桥梁，建立简化的“单梁+单桩”实体有限元模型，其核心在于根据公式同时调整桩径及土弹簧刚度，并验证简化手段的可行性。通过计算“单梁+单桩”模型在整体升温工况下的梁端轴力与形心处线位移及跨中加载工况下的梁端弯矩及角位移，将下部结构及土体对上部结构的约束作用提取出来，转化成加在梁端形心处的一个线弹簧与一个角弹簧的组合，进而转化成2个与梁端形心竖向保持一定距离的线弹簧，作为上部结构梁格模型的边界条件。

1 工程概况

以一座两跨整体式桥台桥梁为计算实例，如图1所示。主梁为2×40m连续预应力混凝土小箱梁，两端与桥台固结，中部桥墩处设置固定支座。

桥台位置处的横断面和桥台具体尺寸如图2、3所示。横桥向6片小箱梁全宽16.7m，高2.0m；桥台宽1.80m，高1.85m，背墙高2.30m，单侧桥台下布置5根钻孔灌注桩，桩径1m，桩长15m，桩台位置的土质为粉质黏土，粉质黏土的地基比例系数取m=10 000kN·m-4。

整体式桥台桥梁采用如下的方式进行施工：在桥位处建造下部结构；张拉正弯矩预应力束，吊装小箱梁形成简支梁体系；中支点浇筑，张拉顶板负弯矩预应力束形成连续梁体系；边支点浇筑，主梁与桥台固结；台后填土，台后土压力传递至结构上。

2 基于统一边界和梁格模型的整体式桥台桥梁分析方法

2.1 概述

基于统一边界和梁格模型的整体式桥台桥梁的分析方法其思路在于：从实体有限元模型中提取出来边界条件，作用于梁格模型上。由于边界相对于主梁有尺度差异，计算需要更为精细，所以采用实体模型提取边界条件。但实体模型往往计算量大，需要对其进行一定的简化，因此考虑将全桥模型转化成“单梁+单桩”模型。

图1 1/2桥梁立面（单位：cm）Fig.1 The elevation of half bridge(unit:cm)

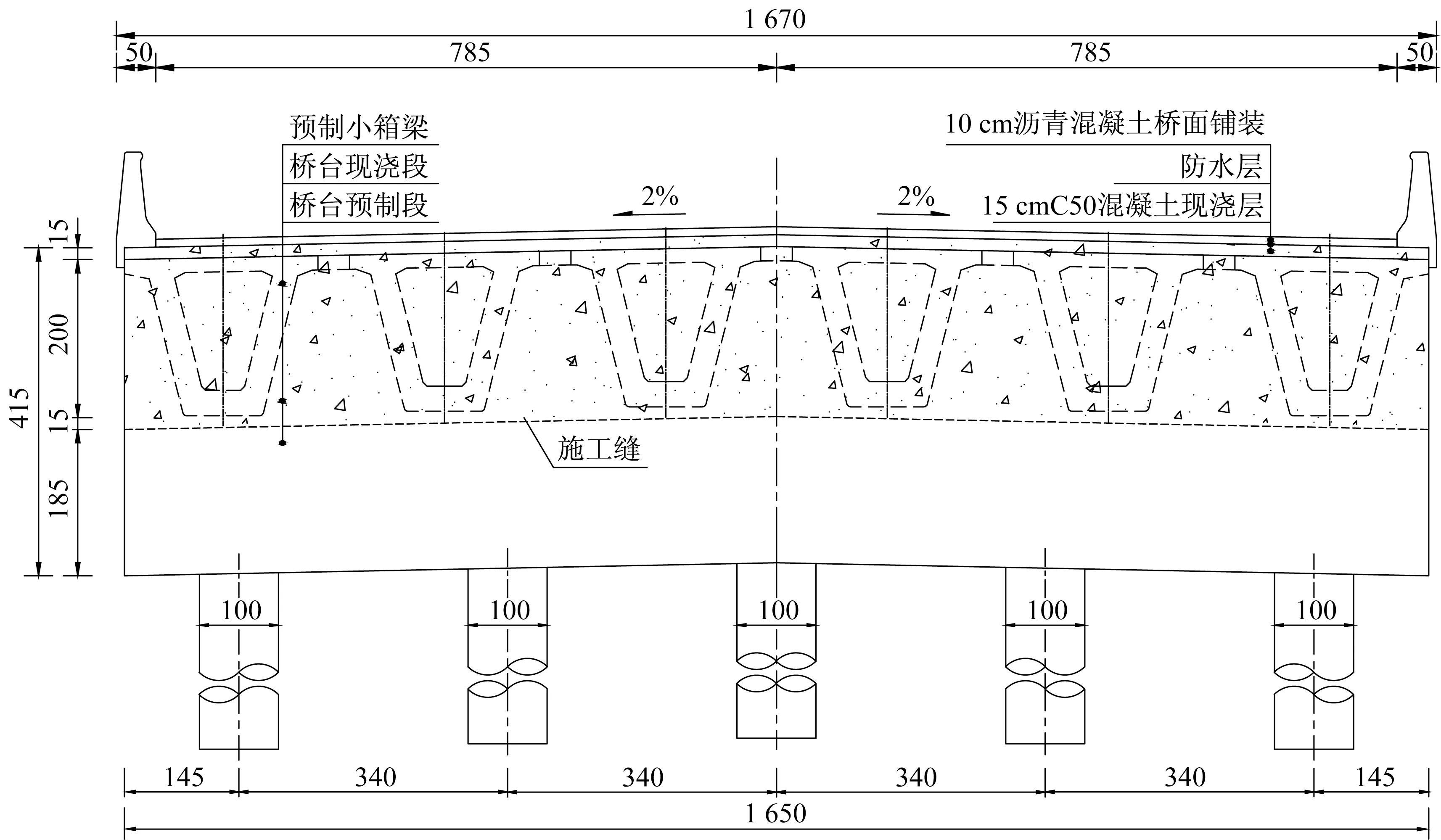
图2 桥台位置处横断面（单位：cm）Fig.2 Cross section at abutment location(unit:cm)

台后土弹簧的非线性导致了体系的不确定性，针对这一问题，需要根据代表性工况对边界条件进行统一。梁格模型的边界条件可以看作是由置于梁端形心处的一个角弹簧和一个线弹簧组成，进一步地可以转化成置于梁端的2个具有一定距离的线弹簧。在“单梁+单桩”模型中，通过整体升温工况，得到梁端轴向力和形心处线位移，求出线弹簧刚度；通过跨中集中力加载工况，得到梁端弯矩及角位移，求出角弹簧刚度。实体有限元模型中提取的边界条件将应用于梁格模型中。

2.2 “单梁+单桩”的简化模型

整体式桥台桥梁的模拟不同于常规桥梁，需要同时建立上部结构和下部结构联合分析。但在建模过程中，可以借鉴常规桥梁全桥简化成“单梁”的思路，将整体式桥台桥梁简化成“单梁+单桩”的模型。本例中存在梁数和桩数不对等的问题，需要强行改变梁或桩的数量。假定梁的数量、尺寸不发生变化，则需要调整桩的数量、尺寸及土弹簧刚度，以保证变化前后下部结构对上部结构的约束效果不变。若关注桩的弯曲受力且认为桥台刚度足够大，令变化前后桩截面总惯性矩不变，有

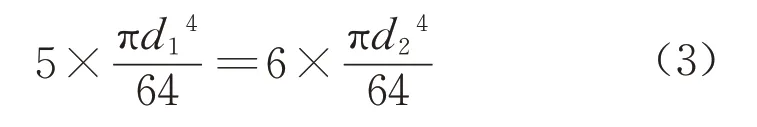
其中，调整前单桩桩径d1=1 000mm，则调整后单桩桩径d2=955mm，调整前后的桩截面如图4所示。

显然，在不考虑桩侧土影响的情况下，这样的简化是成立的。考到桩后总面积的增加，土体的抗推刚度增加，需要对土弹簧刚度做出调整。杨位洸［11］推导了桩的内力与位移的具体计算公式。在其公式的基础上，假定桩底顺桥向线位移为零，弯矩为零，则有桩顶横向位移x0、转角φ0如下：

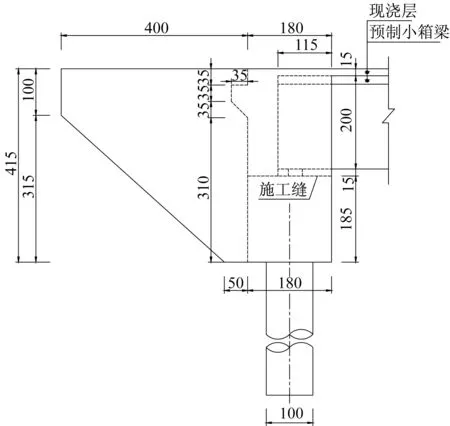
图3 桥台具体尺寸（单位：cm）Fig.3 Dimensions of the abutment(unit:cm)

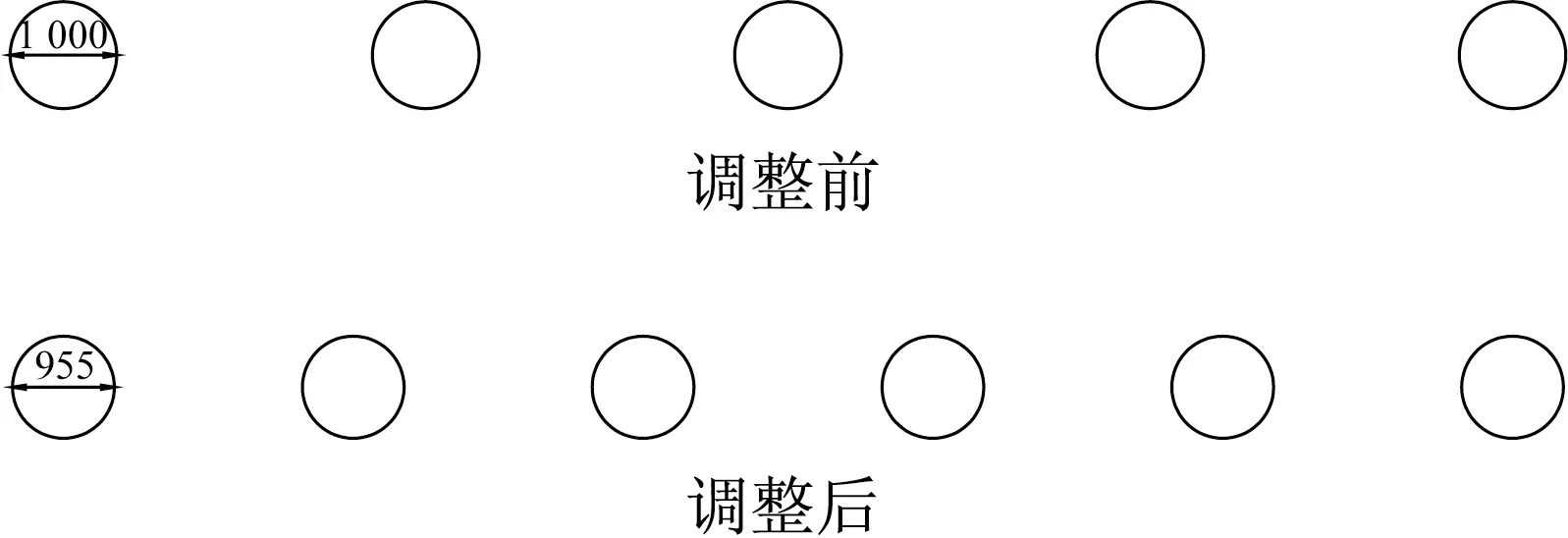
图4 调整前后的桩截面（单位：mm）Fig.4 The pile section before and after adjustment(unit:mm)

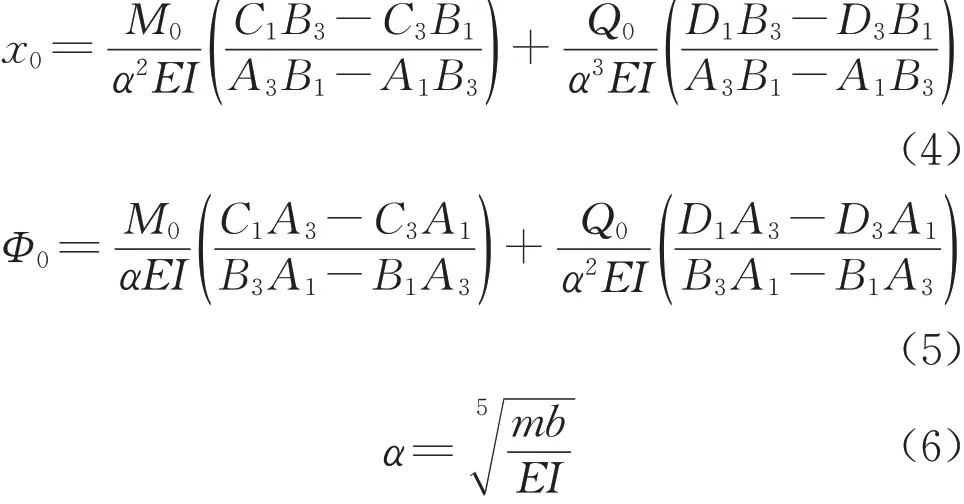
其中，M0为桩顶弯矩，Q0为桩顶水平力，m为地基比例系数，α为桩变形系数，b为桩计算宽度，E为桩材料弹性模量，I为桩截面抗弯惯性矩，A、B、C、D项都是与α有关的参数。由于分式较为复杂，若令刚度不变就需要令桩变形系数α不变，已知调整前的桩截面惯性矩I1等于调整后桩截面惯性矩I2，若使调整前桩变形系数α1与调整后桩变形系数α2相等，有

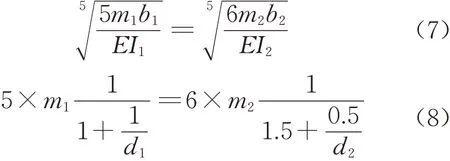
式中：下角标1表示调整前，下角标2表示调整后，即m1为调整前的地基比例系数，m2表示调整后的地基比例系数，b1表示调整前的桩基计算宽度，b2表示调整后的桩基计算宽度。已知d1=1.000m，d2=0.955m，m1=10 000.0kN · m-4，则 m2=8 431.5kN·m-4。关于此推导的理想解释是，虽然变化前后桩的截面抗弯惯性矩没变，但桩后总周长增加导致桩土相互作用面积增加，只有减小地基系数m（相当于减小土弹簧刚度），才能保证变化前后下部结构对上部结构的约束不变。

为了验证简化模型的可行性，分别建立简化前、简化后仅调整桩径和简化后同时调整桩径与土弹簧刚度的下部结构模型，对3个模型的桩顶施加相同大小的z向弯矩105kN·m，如图5所示。

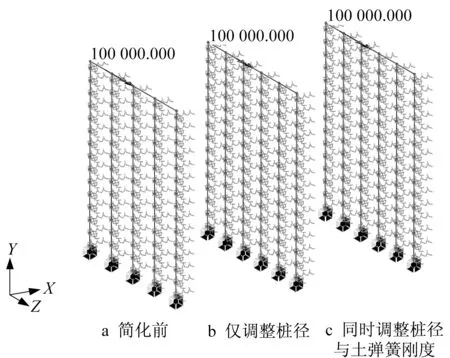
图5 相同弯矩下的3种下部结构模型Fig.5 Three substructure models under the same bending moment

桩身的位移和转角结构如图6所示。

对3个模型的桩顶施加相同大小的x向水平力105kN，如图7所示。

桩身的位移和转角结构如图8所示。

从图6、图8中可以看出，只调整桩径得到的桩身刚度与简化前的模型相比具有一定的误差，尤其在桩顶部，相同荷载下的位移与转角误差较大。而同时调整桩径与土弹簧刚度得到的桩身刚度与简化前的模型相比误差很小，说明这种简化是可行的。

建立“单梁+单桩”的实体有限元模型如图9所示。其中，混凝土用Solid单元模拟，预应力钢绞线及钢筋用Truss单元模拟。混凝土、钢筋与钢绞线都视为均匀弹性体，以弹性模量与泊松比表示结构的材料特性。严格按照实际尺寸建模，z轴沿桥梁纵向，y轴竖直向上，x轴沿桥梁横向。

图6 3种下部结构模型在相同弯矩下的桩身变形Fig.6 Pile deformation of three substructure models under the same bending moment

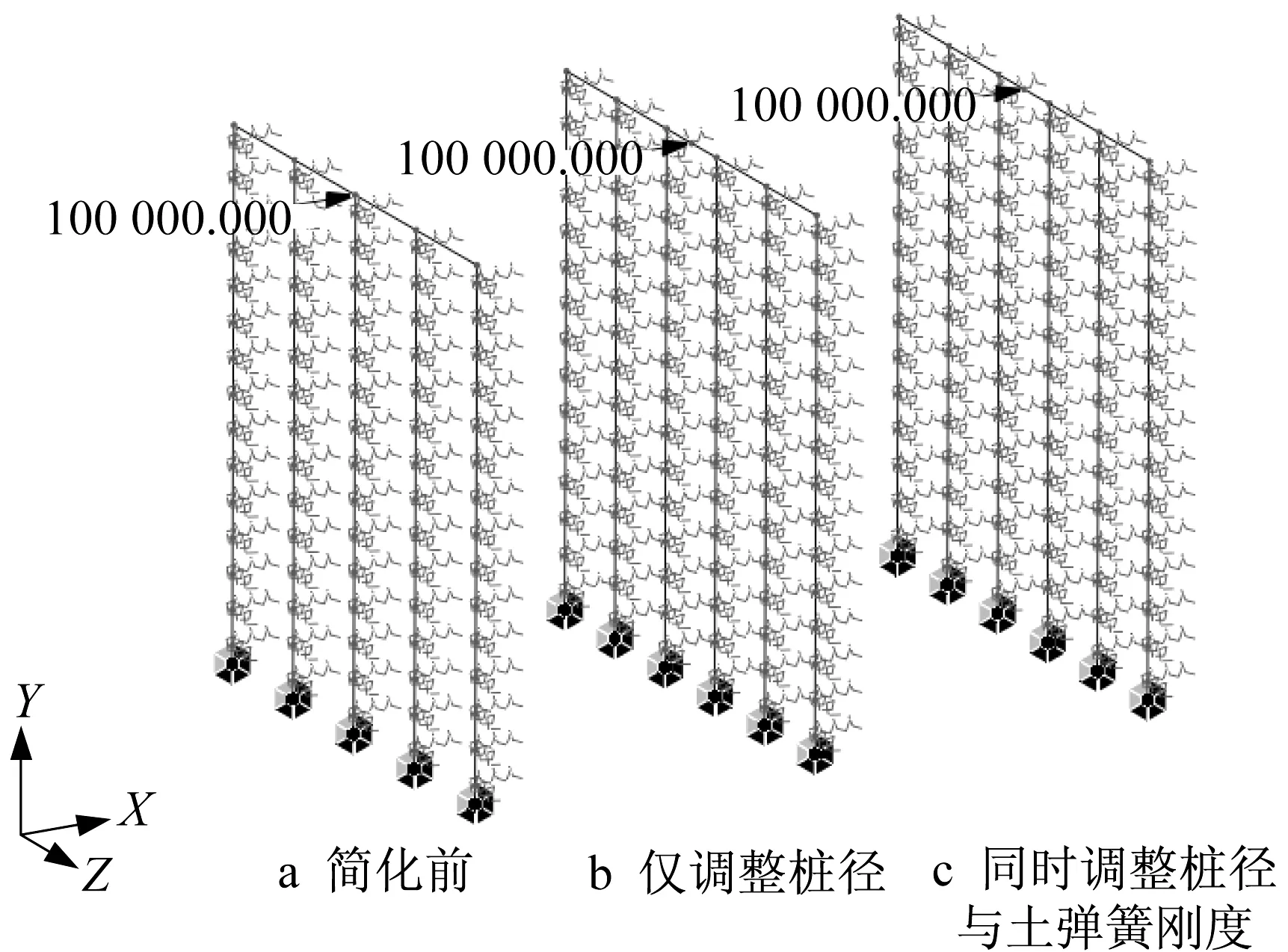
图7 相同水平力下的3种下部结构模型Fig.7 Three substructure models under the same horizontal force

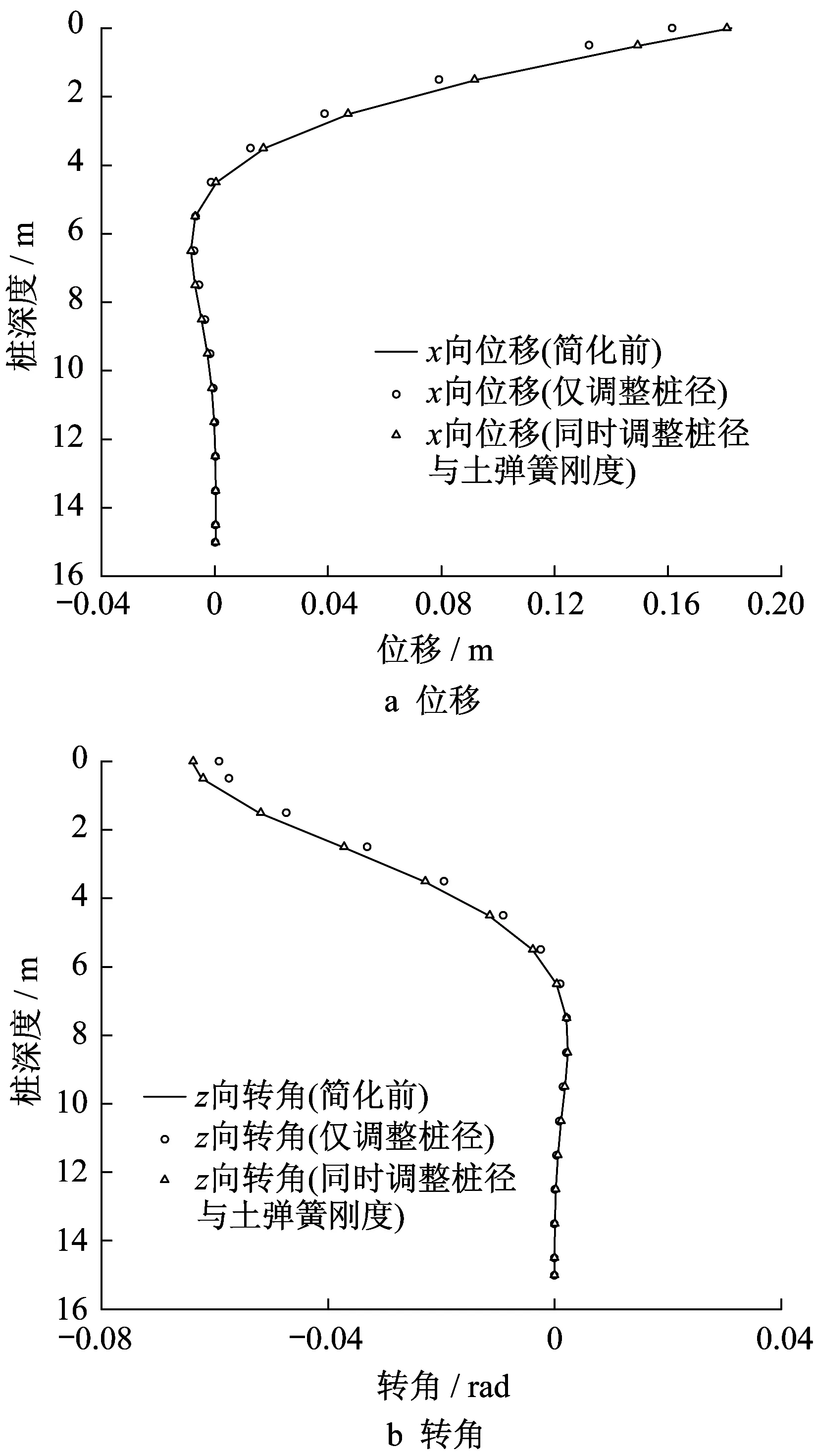
图8 3种下部结构模型在相同水平力下的桩身变形Fig.8 Pile deformation of three substructure models under the same horizontal force

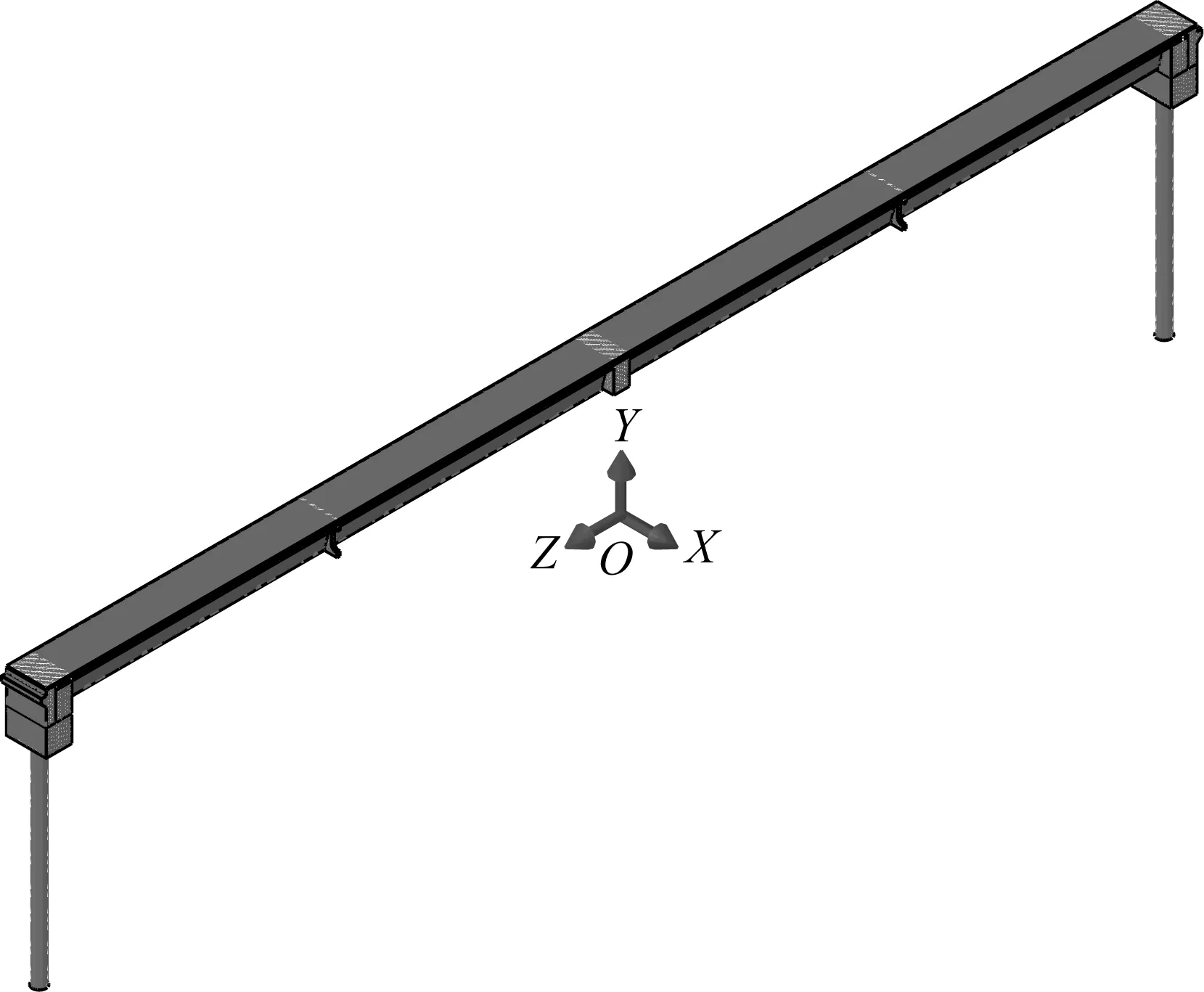
图9 “单梁+单桩”模型Fig.9 The“single beam+single pile”model

台后及桩后的土弹簧布置如图10所示。台后在每约0.2m×0.2m的尺寸范围内布置一个土弹簧，桩后每隔1m的深度布置一个土弹簧，土弹簧刚度根据计算取值。

图10 土弹簧布置Fig.10 Soil spring arrangement

2.3 基于“单梁+单桩”模型的上部结构边界条件

拟将“单梁+单桩”模型的相关计算结果转换成上部结构的梁格模型的边界条件，用于梁的组合工况计算中，思路如下：

将梁格模型的边界条件处理成一个约束梁端位移的线弹簧与一个约束梁端转动的角弹簧，如图11所示。线弹簧刚度及角弹簧刚度由“单梁+单桩”模型在以下2种特定的工况计算：①在整体升温10℃的情况下，计算梁端的轴力和形心处线位移；②在单跨跨中施加1 000kN的集中力时，计算梁端的弯矩和角位移。

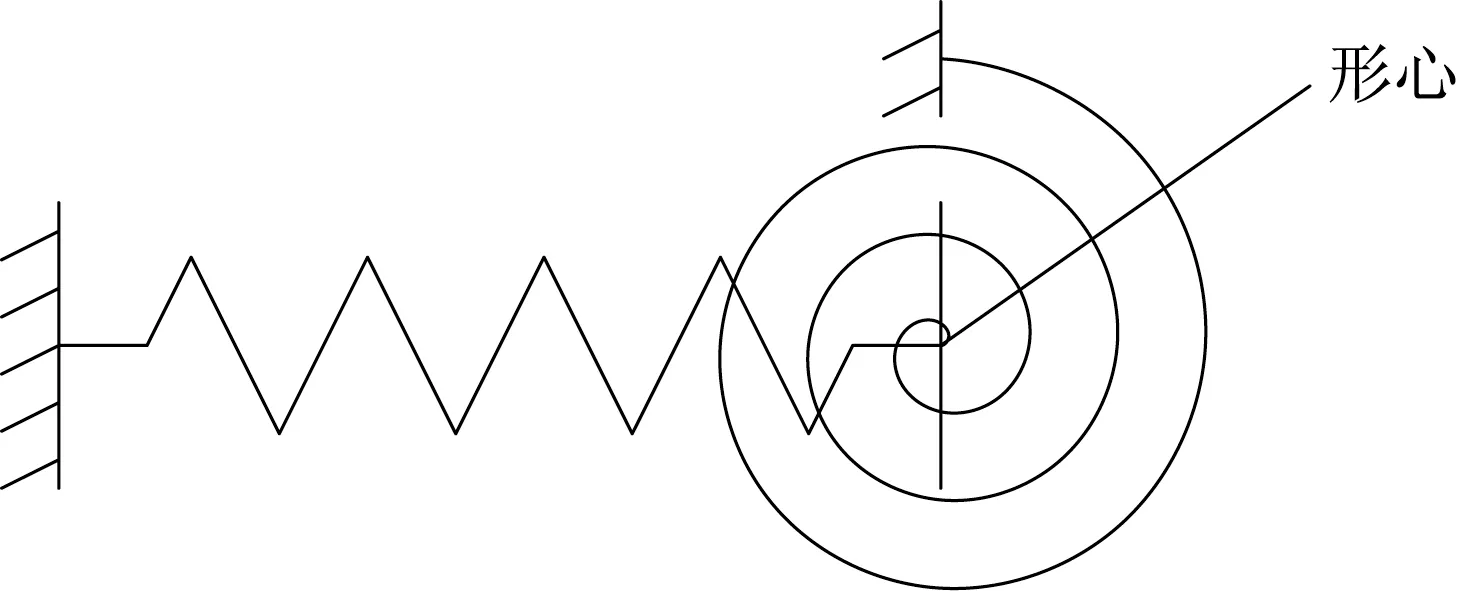
图11 置于梁端形心位置的角弹簧与线弹簧Fig.11 An angle spring and a wire spring placed at the centroid of the beam end

如图12所示，整体升温10℃，梁端的轴力为961.4kN，梁端形心线位移为3.26mm。根据计算获得线弹簧的刚度kl为：

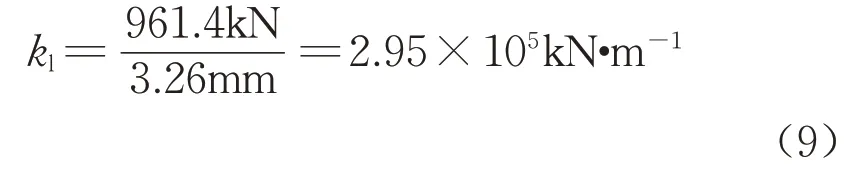
如图13所示，单跨跨中施加1 000kN的集中力，梁端弯矩为2 858kN·m，梁端角位移为：根据计算获得角弹簧的刚度kr为：

图12 整体升温情况下的物理量Fig.12 Quantities under the condition of overall heating

进一步地，将角弹簧与线弹簧的组合转化成2个有一定距离的线弹簧，设转化前角弹簧刚度为kr，线弹簧刚度为kl；转化后2个线弹簧组的刚度分别为k1和k2。如图14所示，转化前后应保证在相同轴力下的位移及相同弯矩下的转角不变，存在以下的刚度换算关系：

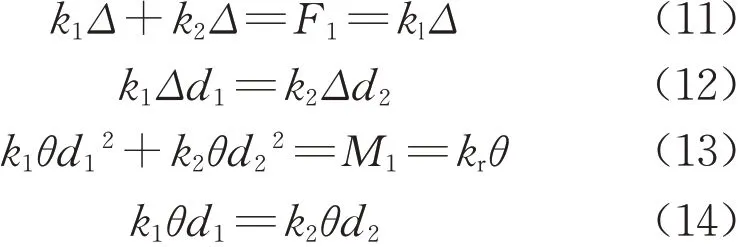
将刚度换算公式简化后有

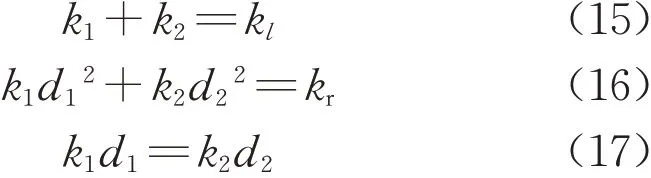
设d1=4m，求解得

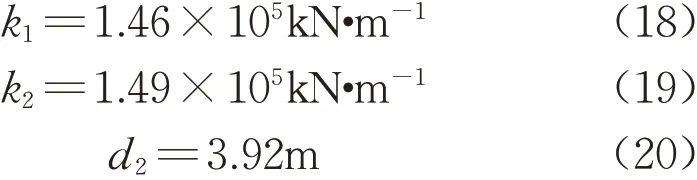
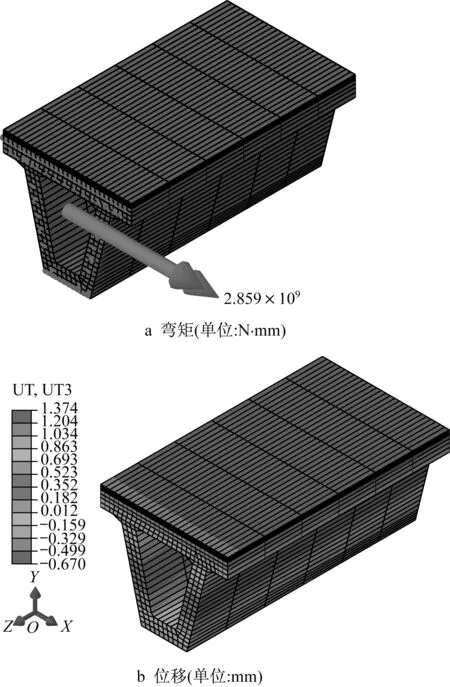
图13 单跨跨中加载情况下的物理量Fig.13 Quantities under single-span loading

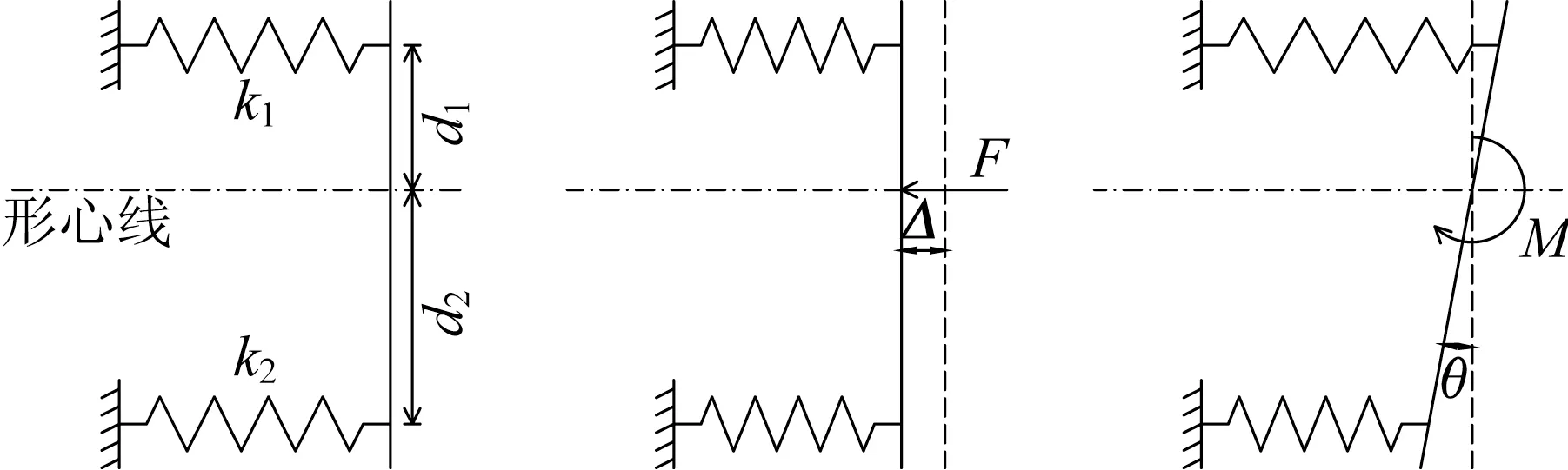
图14 线弹簧刚度求解Fig.14 Calculation of wire spring stiffness

3 计算模型及结果

3.1 梁格模型及荷载

图15 梁格模型的边界条件Fig.15 Boundary condition of grillage model

取预制梁和现浇段作为梁格模型的纵向单元，预制梁和现浇段之间通过虚拟横梁连接，虚拟横梁的厚度为顶板厚度，长度为预制梁外侧加腋根部至现浇段形心，如图16所示。沿顺桥向每1m对主梁进行划分，端部适当加密。建立的梁格模型如图17所示。

图16 梁格模型划分Fig.16 Division of grillage model

图17 全桥梁格模型Fig.17 Grillage model of whole bridge

考虑的荷载包括恒载、二期恒载、活载、整体温度作用、梯度温度作用、基础沉降、徐变。其中，参考《公路桥涵设计通用规范》JTG D60—2015，设计车道荷载采用公路Ⅰ级（即均布荷载标准值为10.5kN·m-1，集中荷载标准值为340kN）；以寒冷地区为基准，混凝土桥梁的有效温度标准值，最低为—10℃，最高为34℃，故考虑整体升降温为22℃；按照《公路桥涵设计通用规范》JTG D60—2015，考虑梯度升降温的影响，其中梯度降温数值为梯度升温数值的一半；基础沉降分成中墩沉降1cm和2个边墩同时沉降1cm这2种情况讨论；与徐变有关的年平均湿度取65%，预制小箱梁认为存放3个月，加载龄期取90d，现浇段的加载龄期为28d。

3.2 计算结果

通过梁格模型查看几种荷载下主梁结构内力，分析如下：

将施工完毕、徐变10年后及一次落架的结构弯矩进行对比，如图18所示。可以看出，尽管从施工步骤上来说，整体式桥台桥梁的恒载主要由简支梁承担，但由于徐变作用，其内力向着一次落架施工的方向上靠拢，且徐变对结构影响很明显。

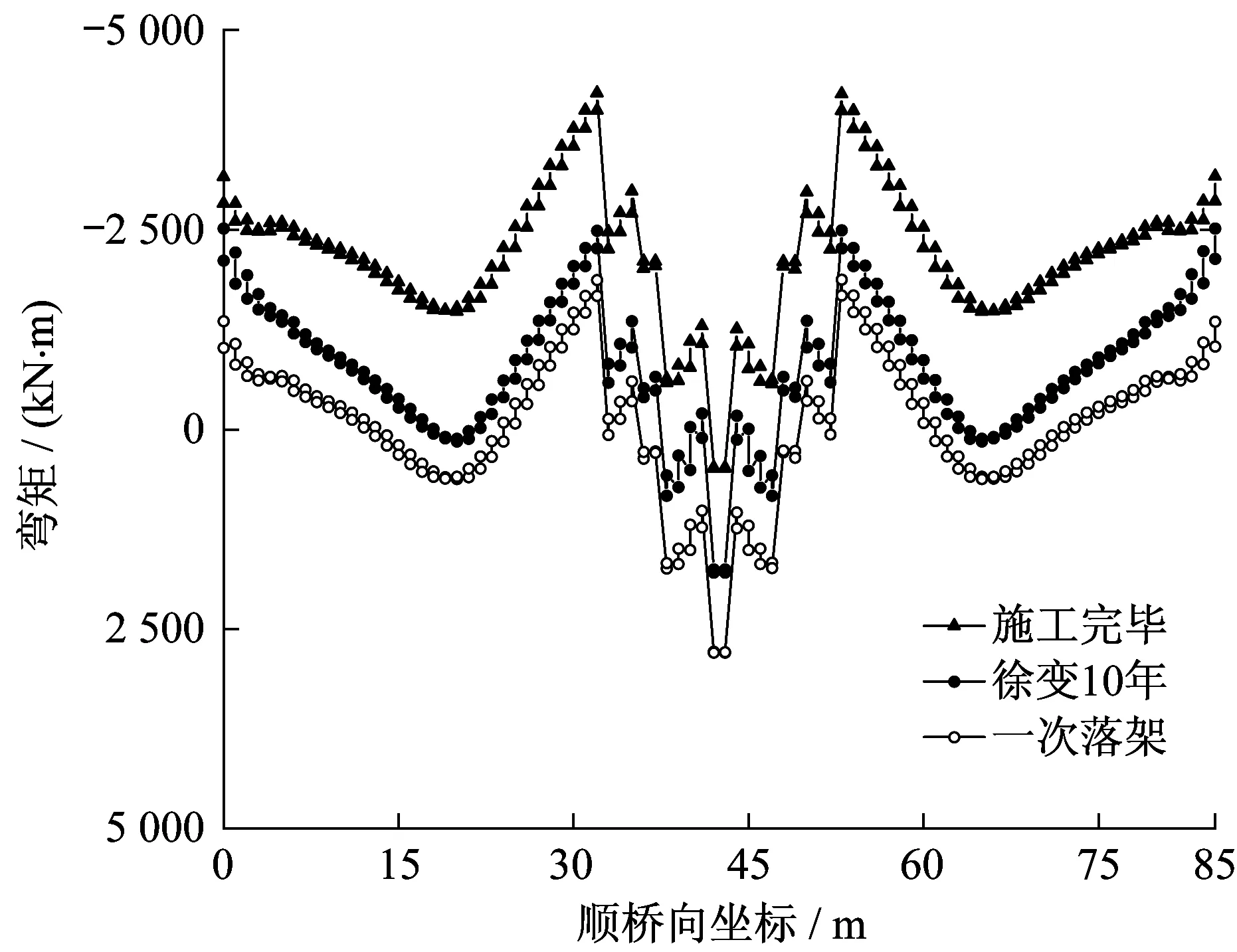
图18 徐变作用下的结构弯矩Fig.18 Moment of structure under creep

整体温度作用下结构弯矩如图19所示。在整体升温工况下，梁端产生负弯矩，整体降温产生正弯矩。整体式桥台桥梁由于受到下部结构及土体的约束，在温度作用下梁体胀缩，端部会受到弯矩作用，这种情况与框架梁较类似。

基础作用下结构弯矩如图20所示。在中支点沉降情况下，由于下部结构的约束作用，会导致梁端产生负弯矩，边支点沉降产生正弯矩。

对几种荷载进行组合，以《公路桥涵设计通用规范》JTG D60—2015中的基本组合为例，取结构重要性系数1.1，恒载作用分项系数1.2，基础变位分项系数0.5，活载作用分项系数1.4，整体温度作用及梯度温度作用分项系数1.4，组合值系数0.75。组合后的弯矩值与规范值的比较结果如图21所示，弯矩值均小于抗力值。由于提取边界条件后得到了一个线性体系，因此能够实现上部结构在多种荷载组合下的验算，方便指导设计工作。

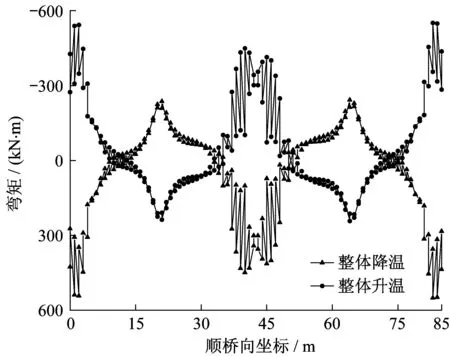
图19 整体温度作用下的结构弯矩Fig.19 Moment of structure under integral heating

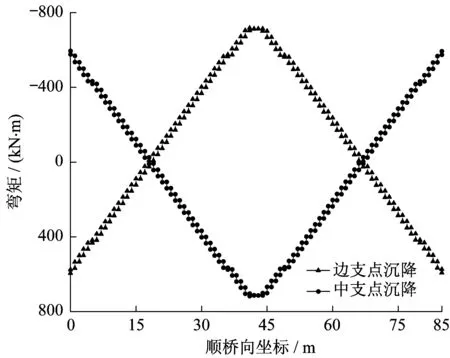
图20 基础沉降作用下的结构弯矩Fig.20 Moment of structure under settlement

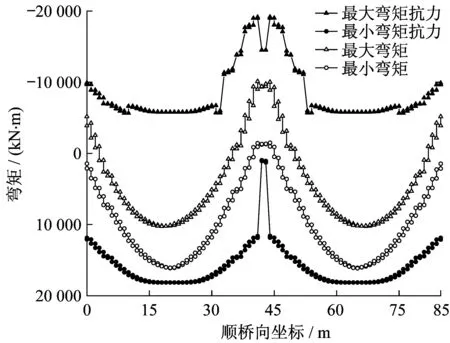
图21 承载能力极限状态的抗弯承载力Fig.21 Bending capacity in ultimate limit states

4 结论

（1）在采用“m”法确定文克勒土弹簧刚度的基础上，提出了一种简化模型，并通过同时调整桩径和土弹簧刚度保证了下部结构对上部结构的约束作用不变。对原下部结构和简化后的下部结构施加相同的单位荷载发现桩端位移接近，验证了简化手段的可行性。

（2）考虑2种代表性工况下简化模型上部结构端部的内力及位移，计算刚度后将2个线弹簧作为边界条件，安装到上部结构的梁格模型的端部。由此能够实现上部结构在不同荷载组合下的验算与调整，为整体式桥台桥梁上部结构的设计提供一种新思路。

（3）在《公路桥涵地基与基础设计规范》JTG D63—2007中，计算桩在非岩石地基中水平位移及作用效应时采用“m”法。而对于岩石地基，则认为其抗力系数Cz不随岩层埋深变化，即Cz=C0，此时计算方法中的土弹簧刚度的确定应按照规范取岩石地基抗力系数C0。

作者贡献申明：

金永学：推导理论公式、数值计算及撰写论文。

徐 栋：提出理论及指导论文撰写。

郑明万：提供数据及整理资料。

贾 栋：提供数据及整理资料。