装配式自复位屈曲约束支撑滞回性能
张超众,郭小农,朱劭骏,高舒羽
(同济大学土木工程学院,上海200092)
屈曲约束支撑(BRB)由于其滞回曲线饱满、耗能能力强、拉压性能相近的特点,越来越多地应用于建筑工程领域,国内外学者也对BRB及BRB框架结构进行了广泛研究[1-9]。虽然BRB弥补了传统中心支撑框架强震下支撑易受压屈曲的缺点,但是相关研究[6-8]表明,由于BRB屈服后刚度较小,结构在强震下易出现层间变形集中现象,且震后存在明显的残余变形。为了改善BRB框架结构的层间变形集中效应,Pan等[10]提出了双屈服点屈曲约束支撑,Wang等[11]也提出了带备用索的屈曲约束支撑,其本质都是通过增大支撑的屈服后刚度使结构的变形模式得到控制。然而上述研究并没有解决BRB框架强震后残余变形较大的问题,当残余层间位移角大于0.5%时,结构的维修成本将超过重建的费用[12]。
自复位耗能支撑既能为结构提供耗能能力,又能提供复位能力,使结构在震后仅产生较小的残余变形甚至无残余变形;同时,支撑与梁柱节点连接方便,不存在自复位节点或自复位墙等与相邻构件变形不协调的问题[13],因而引起了国内外学者的广泛关注。Zhu等[14-15]利用形状记忆合金(SMA)的超弹性和耗能能力,提出了一种自复位耗能支撑;在此基础上,通过增加摩擦耗能装置,进一步提出了自复位摩擦耗能支撑,提高了支撑的耗能能力。Christopoulos等[16]提出了以预应力芳纶纤维筋复位、摩擦装置耗能的自复位摩擦耗能支撑,特殊的构造使支撑无论是受拉还是受压状态,提供恢复力的预应力筋均处于受拉状态。在此基础上,Erochko等[17]和Chou等[18-19]通过串联2组预应力筋,使得支撑的变形能力提高到原来的2倍。刘璐等[20]研究了钢绞线作为复位材料的自复位屈曲约束支撑,然而受限于钢绞线的弹性变形能力,支撑难以满足设计要求。碟形弹簧通过叠合和对合组合可以具有较高的承载力和变形能力,基于此特点,徐龙河等[21]提出预压碟簧自复位摩擦耗能支撑,韩强等[22]提出一种内嵌碟簧型自复位防屈曲支撑,并通过试验验证了其耗能能力和复位性能;但该支撑构造复杂,装配时需要较多的焊接工作,震后损伤部件不易更换。
相比摩擦阻尼器,金属阻尼器具有更稳定的耗能机制。本文在上述研究基础上,提出了一种装配式自复位屈曲约束支撑(assembled self-centering buckling-restrained brace,ASC-BRB)。首先,阐述了ASC-BRB的构造及工作机理,并建立了描述其滞回特性的理论恢复力模型。随后,建立了数值模型并将理论模型与数值模拟结果进行了对比。最后,通过参数分析研究了ASC-BRB关键构造参数对支撑滞回性能的影响规律。
1 ASC-BRB的构造及工作原理
1.1 ASC-BRB的构造
ASC-BRB的构造见图1,由屈曲约束支撑(BRB)和自复位(SC)系统两部分组成。该支撑的耗能内芯在装配时采用全螺栓连接,避免了焊接带来的不利影响,同时便于震后支撑的损伤检测及损伤部件的快速更换。

图1 ASC-BRB的构造Fig.1 Configuration of ASC-BRB
BRB系统由内、外约束套管(简称内管和外管)、2个一字型耗能内芯和连接件组成。内管和外管为方形截面钢管,对耗能内芯起约束作用,防止其受压时出现面外屈曲。内管左端与十字形连接件(左连接件)焊接为一体,外管右端两侧面焊有T型连接件(右连接件),耗能内芯与内外管均采用自攻螺丝连接。一字型耗能内芯包括中间削弱部分的屈服段和两端截面扩大的非屈服段,屈服段和非屈服段间为圆弧过渡段,以减小截面变化部分的应力集中;内芯两侧设置有约束板,以防止内芯绕强轴屈曲;内芯表面粘贴无粘结材料,以减小与约束部件的摩擦;内芯两端开孔,与内外管采用自攻螺丝连接,便于更换。
SC系统由2组钢绞线、碟簧组合、内外管和端板组成。每组钢绞线包括4根钢绞线,2组钢绞线与碟簧组合三者为串联关系,每组钢绞线各有一端锚固于碟簧装置两侧的挡板,另一端分别锚固在内外管两端的端板上。左端板开有十字形槽孔,以便左连接件穿过;左、右端板通过钢绞线的预张力顶紧内外管两端,仅存在接触压力,而无其他连接。
1.2 ASC-BRB的工作原理
ASC-BRB的工作原理见图2。图中F为支撑所受轴向荷载,δ为支撑轴向位移。当支撑处于未受力状态时(图2b),在复位装置预应力筋的预拉力作用下,左右端板挤压内外管,使内外管存在一定的压缩变形;由于内外管轴向刚度比较大,该初始压缩变形较小。ASC-BRB在此阶段处于自平衡状态。
假设ASC-BRB左端固定,当支撑受到向右的拉力F时(图2a),随着外力增大,内管对右端板的压力逐渐减小,外管对左端板的压力也逐渐减小,内外管、耗能内芯和复位装置两端有伸长趋势,直到外力F增加至可以克服预应力筋的预张力,内外管开始出现相对运动。此阶段内外管、耗能内芯和复位装置变形协调,为支撑提供较大的初始刚度。之后内外管不再受力,耗能内芯逐渐受拉屈服提供耗能能力,左右端板距离不断增加使复位装置变形也进一步增加,即预应力筋伸长、碟簧组合压缩,复位装置弹性恢复力进一步增大。若支撑达到某一位移时,耗能内芯未出现破坏,而碟簧组合在外力作用下已经压并,则当外力继续增加时,复位装置中仅有预应力筋进一步伸长。支撑卸载后,复位装置的弹性恢复力克服耗能内芯的屈服力,使得支撑具有较小的残余变形。

图2 ASC-BRB的工作原理Fig.2 Working mechanism of ASC-BRB
若支撑受到向左的压力F(图2c),当F增加至可克服预应力筋的预张力和耗能内芯所需的弹性恢复力时,内外管各有一端与端板脱离并出现相对运动。之后随着外力增大,左右端板在内外套管的推动下距离不断增加,耗能内芯逐渐受压屈服,复位装置弹性恢复力增大。支撑卸载后,复位装置为其提供复位所需的恢复力。与受拉时不同,支撑受压时,内外管推动两侧端板产生相对运动,内外管始终承受轴向压力。
通过上述分析可知,不论支撑受拉还是受压,复位装置两端距离均增大,使其复位能力增加。由于2组钢绞线与碟簧组合串联,因此支撑变形为钢绞线伸长量与碟簧组合压缩量之和,相对仅由钢绞线作为复位系统的支撑,其变形能力显著提高。
2 ASC-BRB的恢复力模型
ASC-BRB系统的恢复力模型可由BRB系统的恢复力模型和SC系统的恢复力模型叠加而成。
BRB系统的钢材强化特性同时包含等向强化和随动强化,并且耗能内芯受压时由于泊松效应和内芯与内外管之间的摩擦作用,其受压承载力略大于受拉承载力。为了便于简化计算,采用只考虑随动强化的双线性弹塑性模型,见图3。图中,δy和Py分别是BRB的屈服位移和屈服荷载;δm和Pm分别是BRB的极限位移和峰值荷载;Kc1和Kc2分别是BRB弹性刚度和屈服后刚度。
现有的基于预应力筋复位的SC系统为双线性弹性模型,而由于提出的ASC-BRB采用2组钢绞线和碟簧组合三者串联为支撑提供复位力,恢复力模型为三线性弹性模型,见图4。图中δat(δac)、δit(δic)、δut(δuc)分别为SC系统受拉(压)时的启动位移、碟簧压并时的位移和极限位移;Pat(Pac)、Pit(Pic)、Put(Puc)分别为SC系统受拉(压)时的激活荷载、碟簧压并时的荷载和极限荷载;Kst1(Ksc1)、Kst2(Ksc2)、Kst3(Ksc3)分别为SC系统受拉(压)阶段的第一刚度、第二刚度和第三刚度。
由于SC系统变形能力较大,并且碟簧组合压并后SC系统表现出屈服后刚度增大的特点。因此耗能内芯可能在碟簧压并前失效,也可能在碟簧压并后失效,从而使ASC-BRB的恢复力模型表现出2种不同特征。为了保证ASC-BRB对结构变形模式的控制效果,要求内芯在碟簧组合压并后失效,则ASC-BRB的恢复力模型见图5。以ASC-BRB首次加载阶段为例,推导其恢复力模型。该恢复力模型共分为9个阶段,各阶段的变形和刚度推导如下。

图3 BRB的恢复力模型Fig.3 Restoring force model of BRB
2.1 支撑不受力时
ASC-BRB未受外力时,在钢绞线预张力T0的作用下,内外管和耗能内芯均受压力,各部件初始压缩变形为
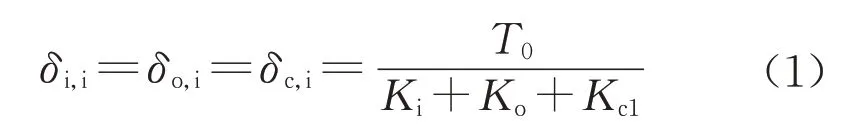

图4 SC系统的恢复力模型Fig.4 Restoring force model of SC system

图5 ASC-BRB恢复力模型Fig.5 Restoring force model of ASC-BRB
式中:δi,i、δo,i和δc,i分别为钢绞线预张力引起的内外管和耗能内芯的初始压缩变形;Ki、Ko和Kc1分别为内管、外管和耗能内芯的轴向刚度,其中


式中:E为钢材弹性模量;Ai、Ao和Li、Lo分别为内管和外管的面积和长度;Ac、Aj、At和Lc、Lj、Lt分别为耗能内芯屈服段、非屈服段和过渡段的面积和长度。
2.2 OA阶段
外力F小于支撑激活荷载Fat时,内外管、耗能内芯和复位装置变形协调,四者为并联关系,支撑第一阶段刚度K1为
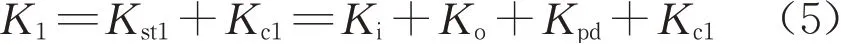
式中:Kpd为2组预应力筋和碟簧组合的串联刚度,即复位装置的刚度。Kpd按式(6)计算:

式中:Kp1、Kp2、Kdz分别为第1组预应力筋、第2组预应力筋和碟簧组合的刚度。其中

式中:Ep为预应力筋的弹性模量;Ap1和Ap2分别为第1组和第2组预应力筋的总截面面积;Lp1和Lp2分别为2组预应力筋的长度。碟簧组合的刚度Kdz可根据国家规范GB/T 1972—2005[23]计算。SC系统启动时,支撑激活荷载为

支撑启动位移δat与各部件初始压缩变形δi,i相同。
2.3 AB阶段
拉力F超过激活荷载Fat后,内外管退出工作,耗能内芯和复位装置继续承担外力,二者为并联关系,直到耗能内芯受拉屈服,则此阶段支撑刚度K2为

由于支撑未受力时,耗能内芯存在初始压缩变形δci,当外力F达到激活荷载Fat时,耗能内芯恢复至不受力状态。因此,耗能内芯屈服时对应的支撑位移δyt为

此时支撑所受拉力Fyt为

2.4 BC阶段
耗能内芯受拉屈服后,随着外力F进一步增大,内外管相对移动距离增加,耗能内芯变形也不断增加,直至碟簧组合达到压并状态。此阶段支撑刚度K3为

参考Miller[24]的建议,耗能内芯的屈服后刚度比取0.03,即Kc2=0.03 Kc1。设碟簧组合自由变形高度为fz,碟簧组合在初始预压力T0作用下的变形量为

当支撑位移为δat时,碟簧组合进一步压缩量为

因此,当SC系统处于第二刚度Kst2范围内时,碟簧组合的最大变形量为

则碟簧组合压并时,支撑的位移δit为

此时支撑所受拉力Fit为

2.5 CD阶段
碟簧组合压并后,随着外力F进一步增大,SC系统刚度仅由2组串联的预应力筋提供,直至支撑达到目标位移。此阶段支撑刚度K4为

2.6 DE阶段
支撑达到目标位移δ后开始卸载。卸载至E点时,根据复位装置和耗能内芯受力状态的不同,存在2种情况,分别见图5中ASC-BRB恢复力模型的实线和点划线。图中实线表示耗能内芯卸载并在复位装置复位力作用下反向受压达到屈服点,而复位装置的碟簧组合仍处于压并状态,此时E点对应支撑位移为δ-2δy;图中点划线表示耗能内芯在达到反向受压屈服点前,复位装置的碟簧组合已恢复至压并临界状态,此时E点对应支撑位移为δit。此阶段支撑卸载刚度为

2.7 EF阶段
根据DE阶段的卸载情况,该阶段亦存在2种情况。
其一见图5中实线,耗能内芯在复位装置复位力作用下处于受压屈服状态,碟簧组合仍处于压并状态,卸载到F点时,碟簧组合处于压并临界状态,此阶段支撑卸载刚度为

其二见图5中点划线,耗能内芯继续卸载并在复位装置复位力作用下反向受压达到屈服点,此阶段支撑卸载刚度为

2.8 FG阶段
支撑继续卸载至内外套管逐渐达到两端平齐并与端板接触的状态,此阶段支撑卸载刚度为

2.9 GH阶段
随着外力进一步减小,内外管、耗能内芯和复位装置协同变形,直至外力F卸载至零。此阶段支撑刚度为

支撑完全卸载之后,由于复位装置的部分预张力与耗能内芯反向受压屈服后的力平衡,支撑无法恢复至初始状态,会产生一定的残余变形δr。δr按式(25)计算:

式中:Pco为支撑复位到原点时耗能内芯的屈服力。由式(25)可见,若能保证Pco≤T0,则δr≤δat。对于自复位屈曲约束支撑,由于其第一刚度K1很大,因此支撑启动位移δat通常很小,则支撑的残余变形δr便可忽略不计。考虑到自复位屈曲约束支撑耗能内芯应变强化及拉压不均匀特性,在自复位屈曲约束支撑设计中,若要实现支撑完全复位,应保证T0≥Pc,max,Pc,max为考虑耗能内芯拉压不均匀特性的最大受压承载力,即T0≥ΦωPy,Φ为耗能内芯受压承载力调整系数,ω为耗能内芯应变硬化系数,根据Miller[24]的建议,可取Φ=1.20,ω=1.35。
需要说明的是,若自复位屈曲约束支撑初始受压,由于外管轴向刚度一般大于内管,支撑达到受压激活荷载前,内外管并非始终变形协调。该结论可通过对支撑各部件取隔离体分析得到。支撑受压时,其启动位移δac和激活荷载Fac可以表示为

支撑受压时,由于SC系统激活后,内外管均受压力,并且内外管与复位装置三者受力为串联关系,因此支撑受压激活后刚度会略小于受拉激活后刚度。
3 有限元模型的建立和验证
3.1 有限元模型的建立
通过有限元软件ABAQUS建立ASC-BRB的精细化模型,以研究ASC-BRB的滞回性能。模型主要部件尺寸如表1所。ASC-BRB整体有限元模型见图6a,其中复位装置模型见图6b。支撑耗能内芯、内管、外管、端板、连接板等部件均采用C3D8R实体单元模拟,钢绞线采用T 3D2桁架单元模拟。除耗能内芯采用Q235钢材外,其余实体部件均采用Q345钢材,钢材材料参数按文献[25]取值。Q235钢材的屈服强度为293 MPa,抗拉强度为465 MPa,弹性模量为202 GPa;材料本构采用可考虑随动强化和等向强化的混合强化模型,强化参数见表2。表中,σ|0为等效塑性应变为零时的材料应力,Q∞和biso为等向强化参数,C1、γ1、C2、γ2、C3和γ3为随动强化参数。Q345钢材采用双线性随动强化模型,屈服强度335 MPa,强化模量取钢材弹性模量的1%。预应力钢绞线的钢丝直径为5 mm,规格为1×7,公称直径为15.2 mm,抗拉强度为1 860 MPa,单根破断荷载为260 kN;材料本构采用线弹性模型,弹性模量取195 GPa;4根钢绞线的总预张力为200kN,通过降温法施加预应力,其中线膨胀系数取1.2×10-5℃-1。已有研究[26]表明,采用弹簧单元模拟碟簧力学性能具有良好的精度。考虑到碟簧组合压并后刚度可视为无限大,采用connector连接器定义非线性弹簧单元,碟簧组合为2片叠合、10组对合,根据规范[23]可求得碟簧组合压并前刚度为7.82kN·mm-1。通过求解力法方程可得,施加200 kN的预张力时钢绞线需降温1 246.85℃。

表1 ASC-BRB模型主要部件尺寸Tab.1 Dimensions of main components of ASC-BRB
模型中连接件与内外管的焊接连接及耗能内芯与内外管的螺栓连接均采用绑定约束,端板与内外管的接触定义为“硬接触”。由于耗能内芯与内外管管壁存在大面积接触,并且加载过程中接触状态不断发生变化,模型采用摩擦接触难以收敛,因此,通过约束耗能内芯的面外平动自由度考虑所受到的侧向约束作用。钢绞线与端板的锚固连接通过耦合钢绞线和端板孔壁相应的节点自由度实现。
支撑一端固定,另一端通过参考点施加轴向位移。加载制度采用等幅递增的位移加载模式,参考相关规范和试验[24,27],并考虑到碟簧压并后,钢绞线变形能力有限,位移幅值分别为±2Δy、±4Δy、±6Δy、±8Δy、±10Δy、±12Δy、±14Δy、±16Δy、±18Δy,Δy为耗能内芯屈服时对应的支撑位移,每个位移幅值循环加载2圈。设支撑与梁的夹角为30°,则支撑加载的最大位移对应的层间位移角为3%。
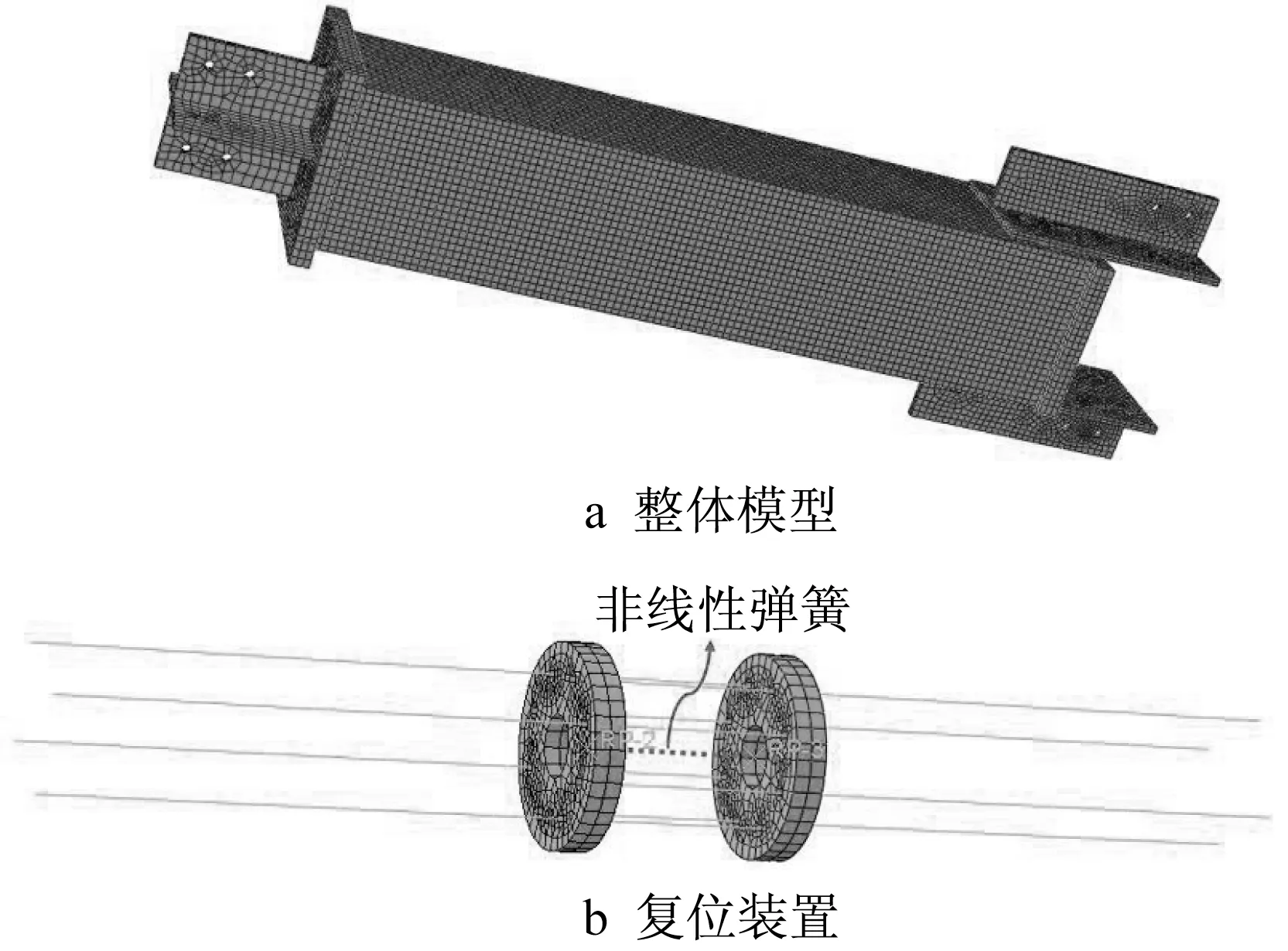
图6 ASC-BRB有限元模型Fig.6 Finite element model of ASC-BRB

表2 耗能内芯材料强化参数Tab.2 Hardening parameters of core plate
3.2 有限元模型的验证
为了保证建模方法的合理性,首先分别对BRB和SC系统进行了模拟,并进行验证。
3.2.1 BRB模型的验证
由于模拟耗能内芯时未考虑内芯受压时与内外管管壁的接触作用,而是直接约束其面外平动自由度,因此需对该模拟方法得到的结果进行评估。采用文献[25]描述的BRB低周往复加载试验的结果进行验证,通过建立与文献相同的耗能内芯模型,并采用相同的加载制度,得到的滞回曲线见图7。从图中可以看出,模拟得到的滞回曲线与试验结果整体吻合较好。试验中内芯与约束部件间的摩擦作用使得BRB受压承载力略大于受拉承载力,因此,模拟得到的受压承载力略小于试验值,误差为6.2%。
3.2.2 SC系统的验证
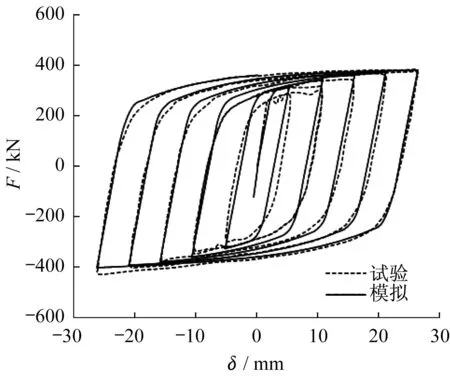
图7 BRB模拟与试验结果对比Fig.7 Comparision of simulation and test results of BRB
按照3.1节描述的方法,建立只包含SC系统的有限元模型,模拟得到的滞回曲线见图8,同时与理论结果进行对比,SC系统的关键参数对比如表3。由图8和表3知,SC系统滞回曲线呈现典型的三段线性特征,模拟结果与理论结果整体吻合程度较高,仅初始刚度误差较大,达到了—25.05%。经分析发现,由于SC系统初始刚度很大,因而启动位移非常小,约为0.05 mm。有限元模拟时,端板的弹性变形会使SC系统的初始刚度显著降低,而理论分析时没有考虑端板弹性变形的影响。采用刚体模拟端板时,模拟曲线与理论曲线几乎完全重合,初始刚度误差仅为—4.10%。SC系统激活荷载为199.85 kN,表明采用降温法施加钢绞线的预应力十分准确。SC系统受压阶段刚度均略小于受拉阶段,如第2节所述,支撑受拉超过启动位移后,内外管不再受力;受压时,内外管均承担压力,由于内外管和复位装置三者串联使得SC系统受压刚度略小于受拉刚度。从表3也可看出,由于内外管截面面积比较大,轴向刚度较大,因此SC系统受拉与受压刚度相差很小,为了简化分析,可认为SC系统拉压性能相同。
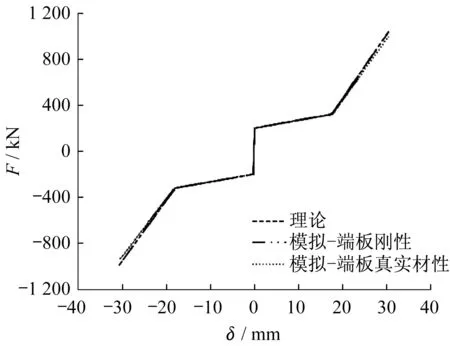
Fig.8 Simulation results of SC system
钢绞线应力和支撑位移关系曲线见图9。可见,该曲线呈现出典型的“V形”特征,无论支撑受拉还是受压,钢绞线均受拉提供复位力。此外,钢绞线应力随支撑位移变化表现出双折线特征,碟簧组合压并前,复位系统刚度较小,钢绞线应力变化较小;碟簧组合压并后,复位系统刚度仅由钢绞线提供,其刚度较大,随着支撑位移增加,钢绞线应力快速增加。从图中也可看出,由于端板弹性变形的影响,支撑位移相同时,钢绞线应力略小于端板刚性的情况。
上述分析结果表明,本文的建模方法可以有效模拟ASC-BRB的滞回性能。
2002年,哈尔滨市规划局委托哈尔滨工业大学规划设计院,一起负责其城市的色彩规划,开始了参与手绘城市色彩的规划,并于同年完成了此方案的制定。
3.3 ASC-BRB的模拟结果
由图10可见,加载至18 mm时,碟簧组合压并,表现出屈服后刚度增大的特点。从图中可见,支撑初始屈服后刚度较小,可充分利用耗能部件的塑性变形耗散地震能量;当支撑达到某一位移后,屈服后刚度显著增加,可减轻楼层的变形集中效应,避免局部楼层变形过大导致结构倒塌。

表3 SC系统关键参数的模拟值与理论值Tab.3 Simulation and theoretical values of key parameters of SC system

Fig.9 Curve of stress of steel strand-brace displacement
图10 还对比了ASC-BRB恢复力模型的理论值与模拟结果,表4给出了支撑各关键参数的对比结果。从图10和表4可以看出,滞回曲线的理论值与模拟结果吻合程度较高,除了初始刚度相差较大外,其余结果最大误差仅为4.14%,表明理论恢复力模型能够有效描述ASC-BRB的滞回特性。

图10 ASC-BRB有限元与理论滞回曲线对比Fig.10 Comparison of finite element and theoretical hysteretic behavior of ASC-BRB

表4 ASC-BRB关键参数的模拟值与理论值Tab.4 Simulation and theoretical values of key parameters of ASC-BRB
4 参数分析
4.1 参数分析模型
进行ASC-BRB设计时,需考虑不同构造参数对支撑滞回性能的影响。在3.3节数值模基础上,考虑钢绞线预张力、耗能内芯面积、钢绞线面积、碟簧对合组数4个关键参数对ASC-BRB滞回性能的影响,并建立13个有限元模型,具体构造参数见表5。各模型命名规则为:字母W代表耗能内芯宽度,字母T代表钢绞线预张力,字母D代表钢绞线公称直径,DS代表碟簧对合组数。W40T200D15DS10为基准模型,基准模型各部件的弹性刚度见表6。
定义强度比β为钢绞线预张力与耗能内芯最大受压承载力的比值,即

由第2节分析可知,若要保证ASC-BRB完全复 位,β值需不小于1。
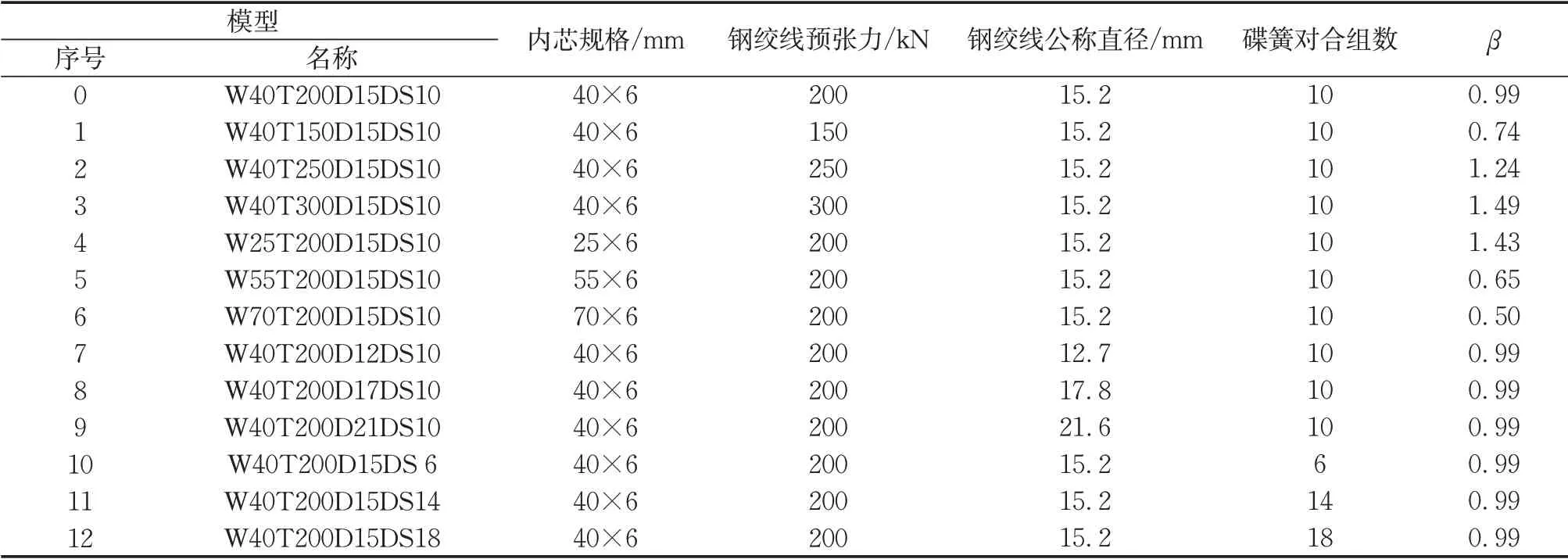
表5 ASC-BRB参数分析模型Tab.5 Parametric analysis models of ASC-BRB

表6 基准模型各部件弹性刚度Tab.6 Elastic stiffness of each component of benchmark model k N·mm-1
4.2 钢绞线预张力的影响
钢绞线预张力分别为150 kN、200 kN、250 kN和300 kN时,ASC-BRB模型的滞回曲线见图11,关键参数模拟结果见表7。表7中,Kv是参数分析模型中改变参数后的部件的弹性刚度;各关键参数均采用量纲一化表示,其值为当前模型模拟结果与基准模型模拟结果的比值。随着钢绞线预张力的增加,支撑激活荷载提高,在相同位移幅值下,W40T 300D15DS10承载力最高,预张力的改变对支撑各阶段刚度没有影响。4个模型的强度比β分别为0.74、0.99、1.24和1.49,残余位移分别为6.37 mm、0.18 mm、0.10 mm和0.06 mm,表明预张力的增加可以有效减小支撑的残余位移。其中,W40T 200D15DS10的强度比为0.99,略小于1,而支撑残余位移仅为0.18 mm,可忽略不计。因此,如前面理论分析,保证ASC-BRB的强度比β不小于1便可以实现支撑完全复位。由于钢绞线预张力的增加,碟簧组合的预压量随之增加,支撑在碟簧组合压并时的位移减小,提前达到较大的屈服后刚度,而受限于钢绞线的弹性变形能力,支撑的极限位移减小。W40T 300D15DS10的预张力为基准模型的1.5倍,而其极限位移仅为基准模型的55.70%。因此,在支撑设计时,钢绞线预张力取值能保证支撑的复位效果即可,从而使支撑具有更大的变形能力。

图11 钢绞线预张力的影响Fig.11 Influence of pretension of steel strands
4.3 耗能内芯面积的影响

表7 ASC-BRB参数分析结果Tab.7 Parametric analysis results of ASC-BRB
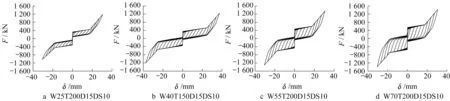
图12 耗能内芯面积的影响Fig.12 Influence of area of core plates
4.4 钢绞线面积的影响
钢绞线公称直径分别为12.7 mm、15.2 mm和17.8 mm和21.6mm时,ASC-BRB模型的滞回曲线见图13,关键参数模拟结果见表7。钢绞线面积的增加对支撑初始刚度K1和屈服后刚度K2、K3影响较小,而屈服后刚度K4显著增大。因为复位装置是由2组钢绞线和碟簧组合串联组成,由表6可知,在碟簧组合压并前,复位系统激活后刚度由刚度较小的碟簧组合控制;而碟簧组合压并后,复位系统的刚度由刚度较大的钢绞线决定。因此,碟簧组合压并前,各模型在相同位移幅值下的承载力几乎相同,而碟簧组合压并后,钢绞线面积的增加使支撑承载力显著增大,可以更有效地抑制结构层间变形快速增加。而支撑所受轴力过大时,会对连接节点和相邻构件产生不利影响。需要注意的是,在施加相同预张力的情况下,钢绞线面积越小,其剩余弹性变形能力越小;W40T 200D12DS10钢绞线面积最小,支撑的屈服后刚度K4和极限变形能力均为最小,结构容易在强震作用下因层间变形过大导致钢绞线断裂。因此,在支撑设计时,可以通过适当增加钢绞线面积提高ASC-BRB对结构变形模式的控制效果。
4.5 碟簧对合组数的影响
碟簧对合组数分别为6、10、14和18时,ASCBRB模型的滞回曲线见图14,关键参数模拟结果见表7。随着碟簧对合组数的增加,支撑屈服后刚度K2和K4略有降低,而K3显著减小。碟簧对合组数的改变对碟簧压并时的支撑位移和支撑极限位移有明显影响。当对合组数为6时,碟簧压并时的支撑位移为11.48 mm(对应层间位移角1.2%),此时支撑能较早地限制结构的层间变形快速增加,而支撑极限位移仅为23.85 mm(对应层间位移角2.44%);当对合组数为18时,碟簧压并时的支撑位移较大,为30.61 mm(对应层间位移角3.1%),此时支撑无法有效控制结构的变形模式,结构可能会出现层间变形集中现象,支撑极限变形能力较强,为44.24 mm(对应层间位移角4.5%)。因此在支撑设计时,需选择合适的碟簧对合组数,使支撑具有足够变形能力而结构的层间变形集中效应又能得到有效控制。

图13 钢绞线面积的影响Fig.13 Influence of area of steel strands

图14 碟簧对合组数的影响Fig.14 Influence of groups of disc springs in series
5 结论
(1)ASC-BRB自复位系统的恢复力模型呈现典型的三段线性特征,碟簧组合压并后,屈服后刚度显著增大,可以使结构在强震下的层间变形更加均匀,减小层间变形集中效应。
(2)ASC-BRB有限元模拟结果与理论恢复力模型整体吻合较好,说明理论恢复力模型能较好地预测ASC-BRB的滞回性能。
(3)对ASC-BRB的滞回性能进行了参数分析,研究了钢绞线预张力、耗能内芯面积、钢绞线面积、碟簧对合组数4个关键参数的影响。结果表明,钢绞线预张力的增加和碟簧对合组数的减少均会使支撑在碟簧组合压并时的位移减小,提前达到较大的屈服后刚度,而受限于钢绞线的弹性变形能力,支撑的极限位移减小;耗能内芯面积的增加对支撑各阶段刚度的影响不明显,能有效提高支撑耗能能力,但会使残余变形增大;控制强度比β不小于1来匹配钢绞线预张力与耗能内芯承载力的关系,保证支撑具有良好复位性能的同时,也具有较高的耗能能力;钢绞线面积的增加能显著提升碟簧组合压并后支撑的刚度,使支撑更有效地防止结构层间变形快速增加。
作者贡献申明:
张超众:提出具体构造,数值模拟,数据分析并撰写论文。
郭小农:提出研究方向,构思研究计划,审阅、修改论文,提出指导意见。
朱劭骏:数据分析,审阅初稿,提出指导意见。
高舒羽:审阅初稿,提出指导意见。

