车用多堆燃料电池系统能量管理与控制策略

周 苏，王克勇，文泽军，张 岗

（1.同济大学汽车学院，上海201804；2.同济大学中德学院，上海201804）

氢燃料电池是氢能源的典型应用，其本质上是一种化学能至电能的能量转换装置，不受卡诺循环限制，考虑热电联供，理论效率可高达90%；若采用绿氢，可真正意义上实现零排放和达到最佳性能［1-2］。随着国家能源战略的调整和节能减排的迫切需求，燃料电池汽车（fuel cell vehicle，FCV）已成为近期的研发热点。

FCV广泛采用“燃料电池/动力电池+电机”的电驱动结构，其中燃料电池、动力电池作为主、辅电源给电机提供电能，动力电池还用于电机负载的“削峰填谷”。能量管理策略（energy management strategy，EMS）根据整车功率需求进行燃料电池和动力电池输出功率的分配，既要满足车辆动力需求，又要实时监控燃料电池和动力电池的状态以及考虑这2个动力电源的效率和寿命等因素。因此，EMS对燃料电池系统的耐久性和燃料经济性具有较大的影响。针对FCV整车EMS问题，卢兰光等［3］分析对比了恒压浮充策略、基于母线电压的MAP图策略、基于SOC（state of charge）的修正策略以及基于SOC和电机需求功率的模糊控制策略，其中后者具有较好的鲁棒性。Feroldi等［4］提出了基于需求功率和SOC的查表法，简单有效，可输出稳定的燃料电池功率。

与纯电动汽车相比，燃料电池汽车在重卡和远程公交领域具有一定的经济性优势；重卡和远程公交车需求功率较大（大于100kW），已有的、技术较为成熟的单堆燃料电池系统（功率小于100kW）满足不了这样的应用需求，多堆燃料电池（multi-stack fuel cell，MFC）系统是一种可能的解决方案。Herr等［5］将预测和健康管理应用于MFC系统，预测其剩余使用寿命。Marx等［6］基于3种典型工况对MFC的串联型和并联型2种结构进行了仿真比较，结果表明并联结构在耐久性和经济性2项指标上均优于串联型。Bernardinis等［7］研究了由3个PEM燃料电堆组成的MFC系统，可根据电堆的健康状态SOH（state of health）独立控制每个电堆。Garcia等［8］提出了一种基于MFC效率最优的功率分配算法，相比于单堆燃料电池，模块化的MFC系统可工作在更佳的区域且减少故障率。

燃料电池汽车能量管理策略的研究主要可归纳为3类，即基于规则的策略、基于优化的策略和基于智能控制的策略。MFC系统的研究主要集中于系统结构、故障诊断与容错、降级工作模式和功率分配，较少涉及基于车辆行驶工况的能量管理策略与多堆协同控制。因此，本文提出了一种基于车辆行驶工况实时识别的车用MFC系统EMS与多堆协同控制方法，深入研究了燃料电池车两级EMS，针对双堆燃料电池分配控制策略进行效率和寿命对比分析，提出兼顾效率和寿命的优化目标函数。

1 燃料电池汽车整车仿真模型

采用的燃料电池整车仿真模型架构如图1所示。驾驶员模型根据整车循环工况的目标车速和实际车速的差值调整需求功率，EMS将需求功率分配至MFC和动力电池2种能量源，最后2种能量源将各自实际可提供的功率传递到车辆模型，车辆模型输出实际车速，并将其反馈至驾驶员模型，从而构成一个闭环的整车仿真模型。

2 包含MFC的燃料电池汽车二级能量管理策略

图2以包含2个电堆构成的MFC为例，描述了燃料电池汽车二级能量管理结构。第一级能量管理策略（图中EMS1）首先根据驱动工况，计算功率需求；然后，基于工况的实时识别结果，将总的功率需求分配至MFC和动力电池。第二级能量管理策略（图中EMS2）对分配至MFC的功率需求在多堆之间进行二次分配，实时控制每个电堆的输出功率。

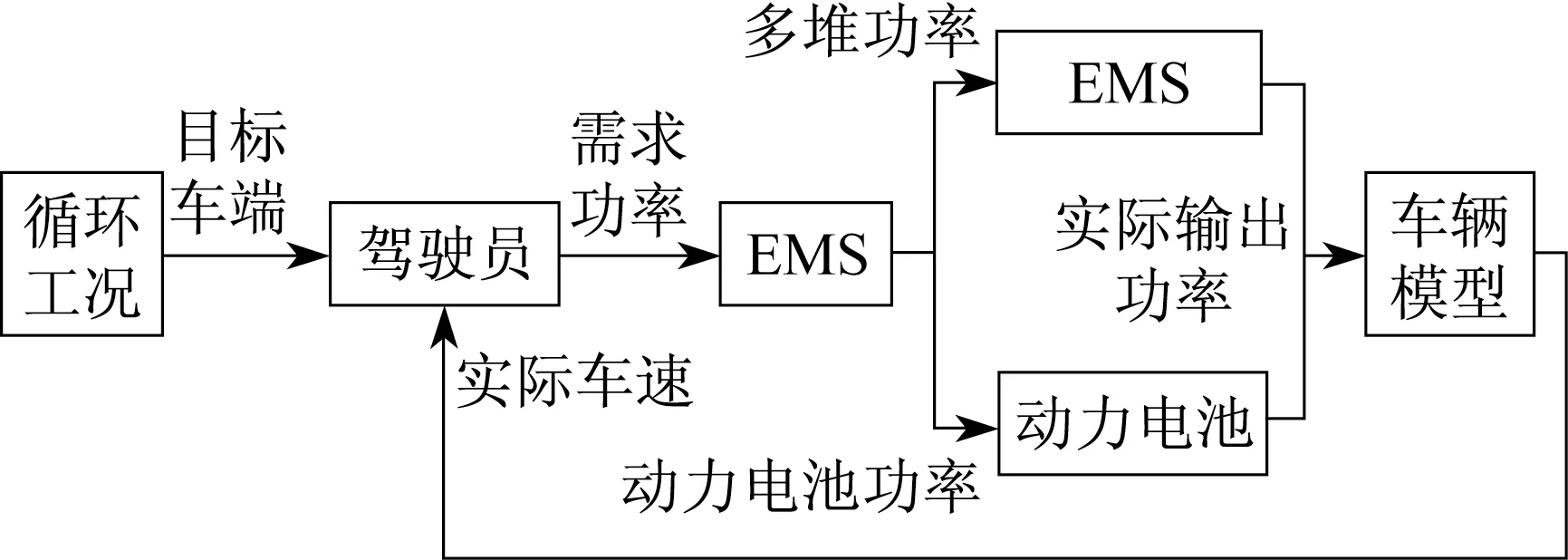
图1 整车仿真模型架构Fig.1 Architecture of vehicle simulation model

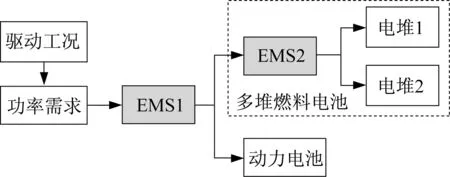
图2 包含MFC的燃料电池汽车二级能量管理结构Fig.2 Principle of multilevel energy management strategy

2.1 第一级能量管理与控制策略EMS1

EMS1采用基于工况识别的自适应功率跟随型能量管理策略。EMS1的基本策略为功率跟随型控制，增加了对实时工况的识别，基于识别结果实现燃料电池汽车的驱动功率自适应分配。为此，针对每种类型工况建立了参数优化的数学模型，并基于遗传算法求解获得每种典型工况的最优EMS1能量管理策略控制参数，用于对实时工况的功率分配自适应调节。

2.1.1 车辆行驶工况识别

国内外已形成了多种类型的标准循环工况，如日本JP10-15复合工况、US06高速工况和欧洲ECE15工况等。本文研究所用的工况数据库选择了分别代表城市工况、市郊工况和高速公路工况的NYCC工况、UDDS工况和HWFET工况，如图3所示。

选择复合等分法对3个典型工况进行运动学片段划分。在构建典型工况数据库时，既要保证样本有效又要样本数量尽可能多，因此，设定识别周期ΔT=100s，更新周期Δω=3s。构建的工况数据库由814个工况片段构成，可以从中提取工况特征，用于建立相应的工况识别模型。

建立工况识别模型首先需要从工况数据库中提取工况特征，原则是尽可能多地包含每个循环工况的特征信息。但是，工况特征参数过多会导致计算量增大，过少又会影响工况识别的准确度。初选10个常用的特征参数，即平均车速、最高车速、平均加速度、平均减速度、最大加速度、最大减速度、停车时间比例、加速时间比例、减速时间比例和匀速时间比例，得到一个814行乘以10列的典型工况数据库矩阵，作为下一步建立工况识别模型的基础样本集。每种工况前5个片段的数据见表1。表中为平均车速，vmax为最高车速，-aa为平均加速度，-ad为减速度，aamax为最大加速度，admax为最大减速度，Ps为停车时间比例，Pa为加速时间比例，Pd为减速时间比例，Pc为匀速时间比例。

初选的10个特征参数之间存在相关性，如平均车速和最高车速存在正相关的关系，加速时间比例、减速时间比例和匀速时间比例的和为1。这不仅会增加工况识别模型复杂度和计算时间，而且还会降低识别准确度。因此，需要对上述典型工况数据进行预处理。数据预处理步骤包含数据标准化和特征参数降维。本文采用Z标准化（Z-score标准化，又称0-1标准化或者标准差标准化）对基础样本集的数据进行标准化处理，采用主成分分析（Principle Component Analysis，PCA）对特征参数进行降维处理。如果PCA定义的累计贡献率达到85%以上，那么降维后的数据足以表达降维前原始数据所包含的信息［9］。如图4所示，经PCA分析，前3个特征参数的累计贡献率为88.69%，从而得到降维后的一个814行乘以3列的数据矩阵Xpca，用于训练工况识别模型。

在车辆实际行驶过程中，工况识别模型需将当前的实际行驶工况识别为与典型工况数据库中最相似的一种类型，用于实现基于工况识别的自适应能量管理。本文选用极限学习机（extreme learning machine，ELM）网络作为工况识别模型，其结构如图5所示。输入层共3个节点（k=3），分别表示3个主成分得分，隐含层节点数为L（需要自己设定），输出层1个节点，表示工况类型编号（1、2、3）。

图3 3种典型工况Fig.3 Three typical driving cycles

表1 部分工况片段的特征参数Tab.1 Characteristic parameters of some driving cycle segments

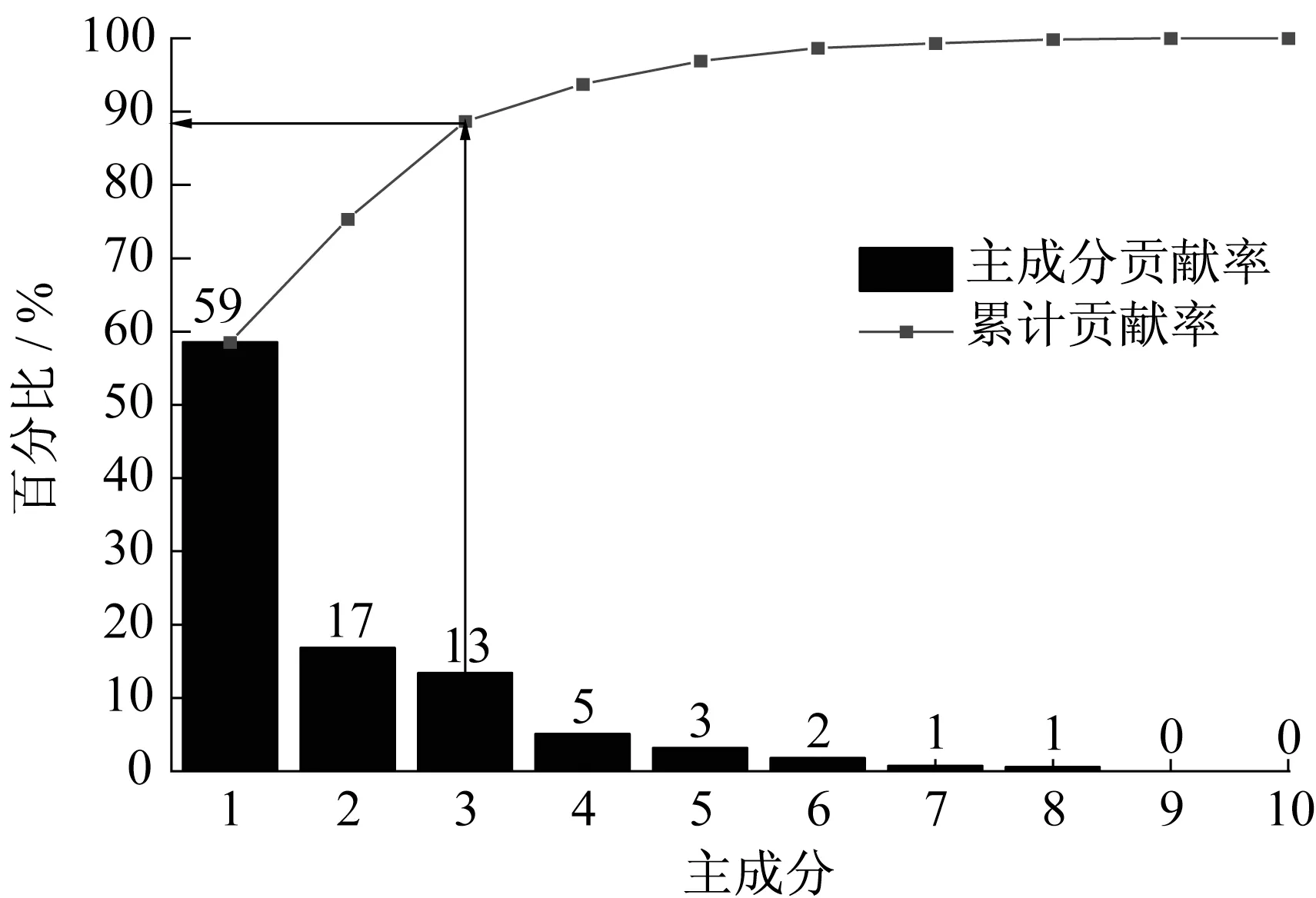
图4 PCA降维结果Fig.4 Results of PCA dimensionality reduction

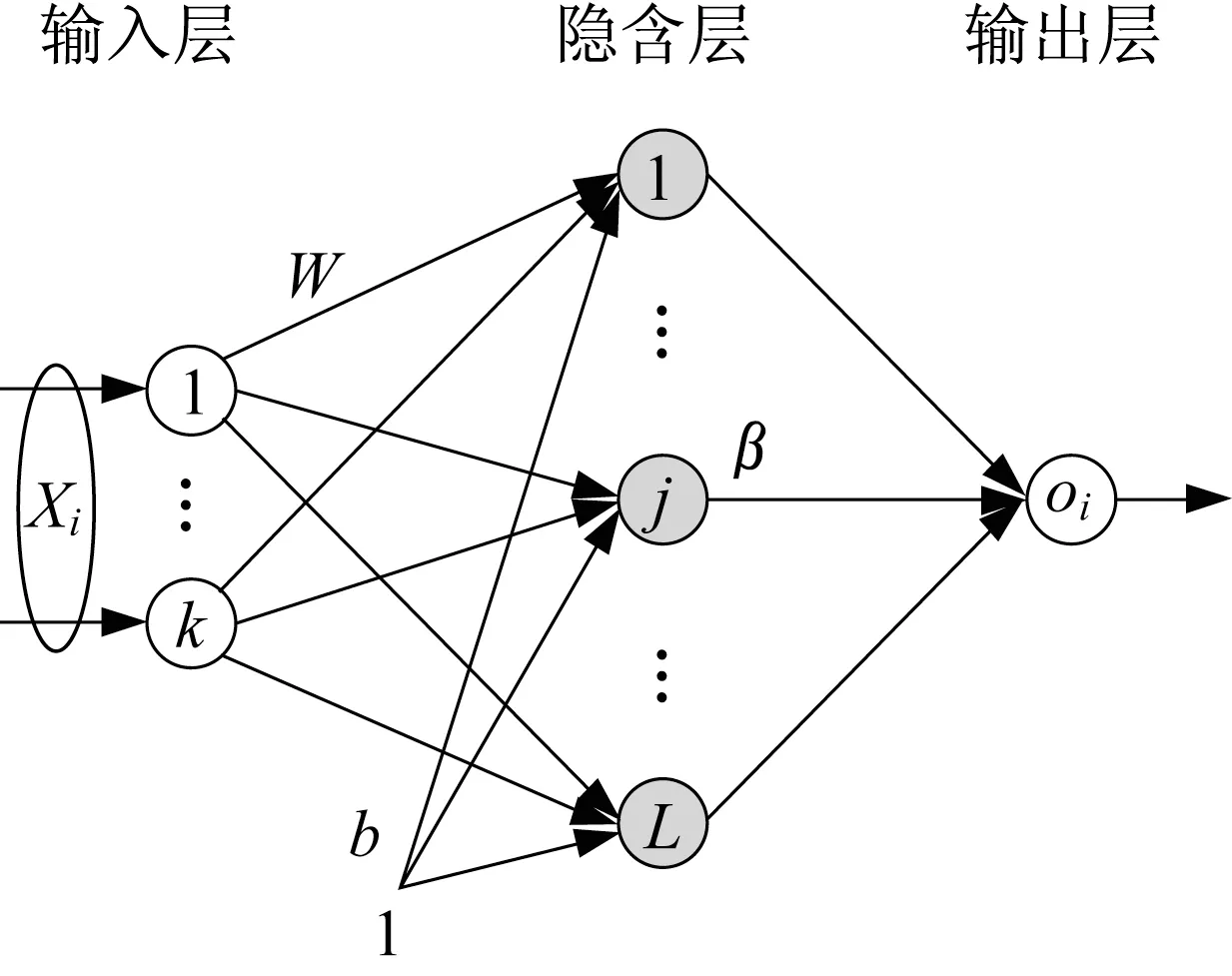
图5 ELM算法网络结构Fig.5 Structure of ELM algorithmic network

2.1.2 功率跟随型能量管理策略

EMS1采用的功率跟随型控制策略是一种较为简单的、基于规则的功率修正控制策略，主要包括燃料电池开关控制子系统和基于SOC的功率修正子系统两部分，前者根据当前的需求功率和动力电池SOC值，给出是否开启MFC系统的信号，后者调节实际输出功率。图6描述了本文采用的功率跟随型控制策略控制逻辑。

2.1.3 基于遗传算法的控制策略参数优化

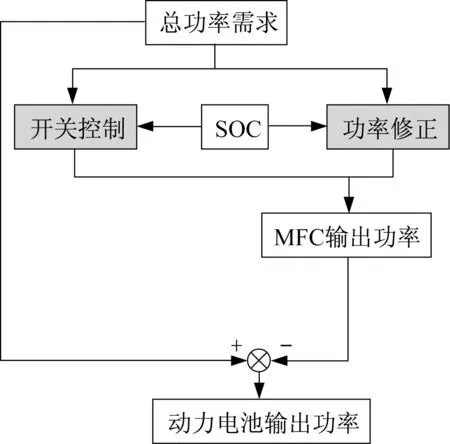
图6 功率跟随型策略原理Fig.6 Principle of power following strategy

EMS1采用功率跟随型控制策略，其中有部分参数值如动力电池SOC允许上下限和最大充电功率、燃料电池输出功率变化的容许斜率等，需要根据使用的动力电池、燃料电池以及工况特征予以优化标定。优化这些待标定参数，可以保护燃料电池和动力电池，提高使用寿命，增强耐久性。燃料电池系统的经济性和耐久性与以上描述的控制策略参数值相关，因此，需要针对每种典型工况分别确定各个最优值［10-12］。对功率跟随型控制策略中的5个关键参数进行优化，如表2所示，x1表示动力电池允许的SOC上限，x2表示动力电池允许的SOC下限，x3表示燃料电池给动力电池的充电功率（单位为W），x4表示燃料电池输出功率最大上升斜率（单位为W·s-1），x5表示燃料电池输出功率最大下降斜率（单位为W·s-1），其中每个参数的允许上下限主要根据相关参考文献和实际经验给出。

表2 功率跟随型控制策略中的关键控制参数Tab.2 Key control parameters in power followingcontrol strategy

表征燃料电池汽车动力系统燃料经济性的目标函数F（X）（等效燃料消耗）为

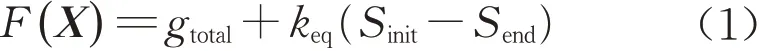
式中：X是由待优化变量组成的控制策略参数向量，gtotal为MFC消耗的总氢气量，keq表示将动力电池SOC的变化转换为等效氢气消耗的转换因子，Sinit、Send分别为动力电池运行初始、结束时的SOC值。遗传算法（Genetic Algorithm，GA）可用于求解复杂的非线性规划和优化问题，相比传统的梯度下降法，可以搜索到更加准确的解空间［13］，并且具有较高的鲁棒性和很好的收敛性。因此，采用GA算法对式（1）进行求解，在满足表2的约束条件下，针对工况数据库选择的3种典型工况，获得了对应的3组最优控制参数Xopt。

2.2 第二级能量管理与控制策略EMS2

EMS2对MFC中每个电堆的输出电功率进行控制，在保证正常工作条件下尽可能地提高MFC的整体效率和/或寿命。首先，仅考虑效率，对目前常用的平均分配、逐级链式分配和效率最优的3种功率控制策略进行分析和对比，其中重点研究效率最优的分配控制策略，建立其效率优化模型，并进行求解和仿真分析。然后，引入兼顾效率和寿命的目标优化函数，研究权衡MFC效率和寿命因素的综合功率最优分配。

2.2.1 功率平均分配策略

功率平均分配策略是一种简单的分配方法，将需要MFC输出的功率平均分配给每个电堆，并同时开启和关闭。每个电堆的实际输出功率可表示为

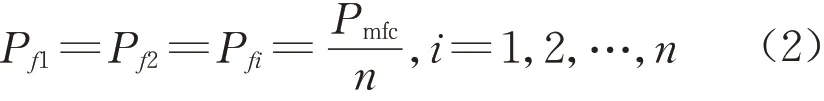
式中：Pfi表示第i电堆实际输出的功率，Pmfc表示EMS1分配给MFC的总需求功率。如果MFC包含双堆，那么每个电堆的输出功率可表示为

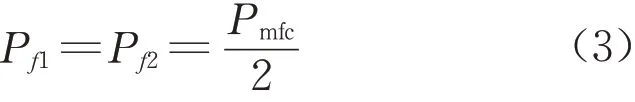
2.2.2 功率逐级链式分配策略

功率逐级链式分配策略的原则是尽量开启最少数量的电堆，每个电堆有其对应的最大可输出功率，当前一个电堆已经达到其最大可输出功率后，再开启下一个电堆，实现逐级的开启和关闭电堆，开启的电堆个数取决于Pmfc的大小。双堆MFC在逐级链式分配策略下的效率η可表示为

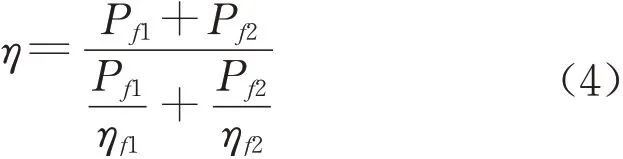
2.2.3 效率最优的功率分配策略

效率最优的分配控制策略是在离线条件下针对已知的应用场景或MFC需求功率工况｛Pmfc（t），t=tI，tI+1，…，tE—1，tE｝，寻找一组最优的MFC中各电堆功率分配方案，使得MFC总效率最大，从而降低氢耗，提高经济性。约束条件共3个，即①分别是所有电堆输出功率之和等于Pmfc；②每个电堆输出功率不能大于其最大可输出功率；③每个电堆输出功率对应的效率曲线。上述优化问题可用如下数学公式描述：

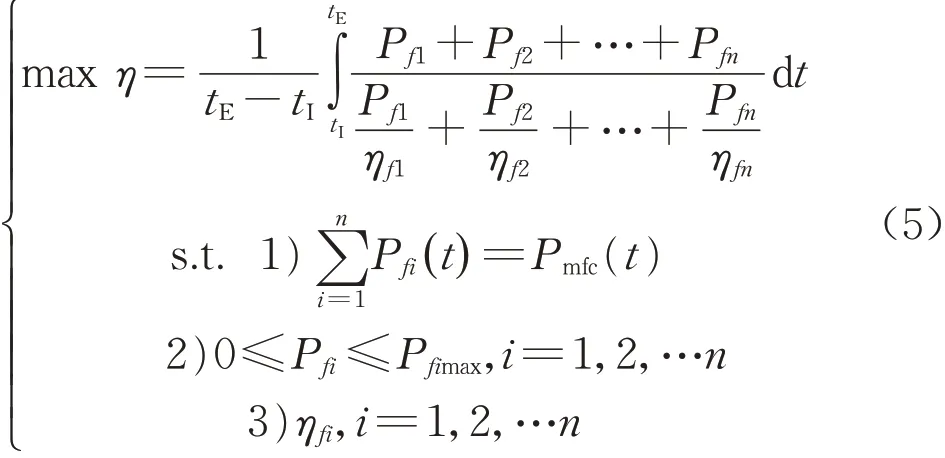
式中，η为MFC总效率，n代表电堆的个数（n≧2），Pfi、Pfimax分别表示第i个电堆的输出功率、最大输出功率，ηfi表示第i个电堆输出功率为Pfi时的效率。

针对双堆MFC系统，n取2即可。针对该类型的非线性规划问题，选用专业优化软件Lingo进行求解。由于max｛Pmfc（t）｝=30kW，MFC需求功率工况｛0≤Pmfc（t）≤30，t=tI，tI+1，…，tE—1，tE｝，取步长为0.1kW，可获得已知的MFC需求功率工况下的最优功率分配方案及其对应的最大效率。

2.2.4 考虑寿命因素的第二级能量管理策略EMS2

上述EMS2没有考虑寿命因素，但是，在电堆实际使用过程中无法避免性能衰减和剩余使用寿命（remaining useful life，RUL）降低的情况。电堆的使用寿命不仅取决于它当下和以前的输出功率，还受到其制造工艺、工作环境和操作条件等因素的影响，是一个非常复杂且与多因素关联的问题，目前还没有一种模型或方法能够准确描述寿命衰减和老化的过程。

文献［5］提出了一种用于描述燃料电池的剩余使用寿命与输出功率之间关系的简化模型，如图7所示。该简化模型与输出功率和效率关系类似，当电堆的输出功率处于中间某个区域时，RUL达到最大值，该区间称为最佳寿命工作区间；当输出功率不在最佳寿命工作区间，都会导致RUL下降。RUL曲线的形状由每个电堆自身的特性决定。

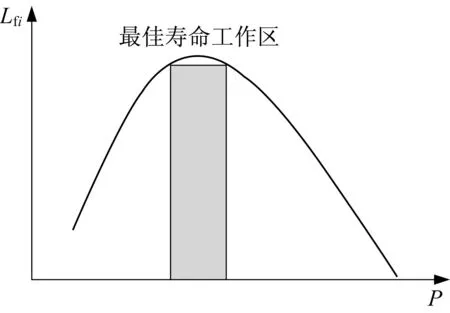
图7 RUL与输出功率的近似关系曲线Fig.7 Approximate relation curve between RUL and output power

前文优化模型中目标函数仅包含系统总效率，研究的是效率最优的分配控制策略。基于以上RUL模型，将影响电堆的寿命因素加入到目标函数，则可以实现权衡系统效率和寿命后的综合最优分配。在式（5）中，将目标函数修改为

式中第一项为效率因素，其中kη为效率因素的权重，第二项为寿命因素，其中kT为寿命因素的权重，TRUL为系统平均剩余使用寿命，其定义如下：

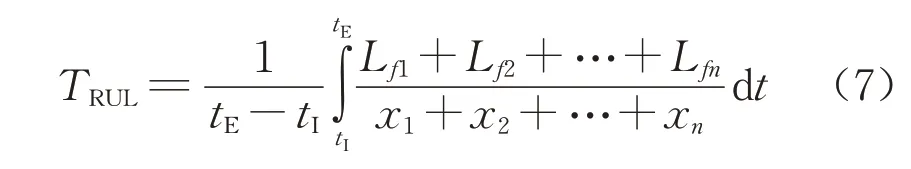
在式（5）中，约束条件(3)增加

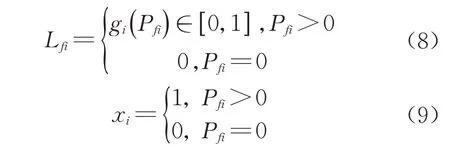
式中，Lfi表示第i个电堆的剩余使用寿命，是一个量纲一化的量，表示剩余寿命的比例，gi（Pfi）表示第i个电堆输出功率与剩余使用寿命的函数关系，xi表示第i个电堆是否开启。

引入兼顾效率和寿命的目标优化函数（6），采用前面介绍的优化数值求解方法，可获得权衡MFC效率和寿命因素的综合功率最优分配。

3 仿真结果与对比分析

3.1 第一级能量管理与控制策略仿真对比分析

基于图1所示的仿真系统，仿真分析是将所有功能模块集成后的完整仿真分析和对比过程。为体现工况识别模块对EMS1中控制参数的自适应调整，仿真所用的工况是将NYCC、UDDS和HWFET按顺序连接后组成的一个复合工况。该工况持续时间为2 734 s，模拟从拥堵的城市开始，中途经过市郊，最后驶上高速工况的一个完整行驶过程，全程共30.4 km。仿真初始SOC值设为0.7，步长设置为0.1 s。

3.1.1 工况跟随性

车辆动力响应好坏可通过车辆实际行驶速度与工况目标车速之间的差异来体现，图8给出了仿真的实际车速和目标车速。从图中可看出工况跟随性较好，但局部放大图显示，部分区间的实际车速和目标车速间存在大约1km·h-1的偏差。总体来说，整车仿真模型满足了车辆动力性的需求，实际车速可以很好跟随目标车速。

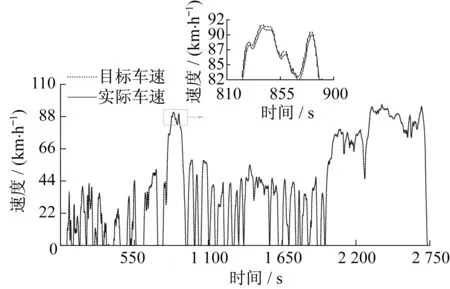
图8 仿真目标车速和实际车速Fig.8 Simulated target speed and actual speed

3.1.2 动力电池系统

SOC是动力电池重要的一个状态，其过高或过低都会对动力电池造成损害，因此必须控制SOC在合理范围，即EMS1中定义的SOC允许上下限。仿真过程中SOC变化曲线如图9所示，初始SOC值设为0.7，行驶在城市道路工况区间（0至750s），需求功率变化频繁且较为激烈，燃料电池系统动态响应较差，这部分需求功率主要由动力电池提供因此，SOC一直呈现下降的趋势。城市道路工况结束后，SOC维持在0.6左右，仅呈小幅波动，EMS1可以有效地将SOC维持在其合理的范围。

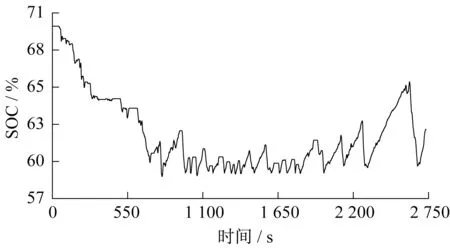
图9 动力电池SOC变化曲线Fig.9 SOC curve of power battery

3.1.3 工况识别结果

针对仿真的复合工况，工况识别结果如图10所示。从图中可以看出，2种工况连接处因工况特征不明显，容易发生错误识别的情况，但整个仿真过程的工况类型识别准确率为87.49%，达到工况识别的目的。

图10 工况识别结果Fig.10 Results of driving cycle identification

3.1.4 工况仿真对比分析

NYCC工况下各控制参数（x1，…，x5）、氢燃料消耗（gtotal，g）、动力电池SOC的变化（DSOC）和等效燃料消耗（geq，g）优化前后的值见表3。参数优化后，实际氢耗（gtotal）增加了0.83g，动力电池SOC的变化（DSOC）减小了0.01，相应地等效燃料消耗（geq）从12.55g减少到12.35g，整个燃料电池系统的燃料经济性提高了1.54%。

表3 NYCC工况下优化前后参数比较Tab.3 Comparison of parameter optimization in NYCC

UDDS工况下优化前的控制策略参数（x1，…，x5）与NYCC工况一致，各优化参数、氢燃料消耗（gtotal）、动力电池SOC的变化（DSOC）和等效燃料消耗（geq）优化前后的比较见表4。从表中可看出，参数优化后氢耗（gtotal）增加了5.42g，但是由于动力电池SOC的变化（DSOC）减小了0.08，从而将等效燃料消耗（geq）从58.07g减少至54.13g，燃料经济性提高了6.78%。

表4 UDDS工况下优化前后参数比较Tab.4 Comparison of parameter optimization in UDDS

HWFET工况下参数优化前后的各参数和指标的对比见表5。参数优化后氢耗（gtotal）虽然增加了15.33g，但动力电池SOC的变化（DSOC）从0.24减小到0.07，等效燃料消耗（geq）从77.48g减 少 到72.17g，燃料经济性提高了6.85%。

表5 HWFET工况下优化前后参数比较Tab.5 Comparison of parameter optimization in HWFET

基于GA算法，对EMS1中5个控制参数进行优化，获得了3种典型工况的最优参数值，通过对参数优化前后的EMS1的效果比较，发现NYCC工况、UDDS工况和HEFET工况下等效燃料经济性分别提高了1.54%、6.78%和6.85%。

3.2 第二级能量管理效率仿真对比分析

3.2.1 3种功率分配策略对比

为了直观体现2.2节介绍的3种功率分配策略的特点，图11给出了30kW双堆MFC系统EMS2实施相应功率分配策略的系统效率曲线。图中效率最优策略和逐级链式策略下的系统效率曲线在Pmfc为10.375 kW和15.000 kW处分别出现拐点。前者拐点左侧区域内2种功率分配策略下的系统效率相同，且都高于平均分配策略下的系统效率。采用平均分配策略，MFC系统效率曲线与一个单堆燃料电池系统的相同，体现不出MFC的优势。拐点10.375 kW右侧区域内效率最优分配与平均分配策略下的系统效率相同，且都高于逐级链式分配策略下的系统效率。逐级链式分配策略下的系统效率在其拐点15 kW达到一个极小值，且在左右邻近区域效率都较低。逐级链式分配策略下需求功率较小对应的MFC系统效率较高，效率最优分配策略下整个需求功率区间都可保持较高的效率，扩大了燃料电池系统的高效工作范围。综上，EMS2采用效率最优功率分配策略，有利于MFC工作在高效率区间，提高FCV燃料经济性。

图11 EMS2三种功率分配策略的MFC系统效率曲线Fig.11 Efficiency curves of MFC system based on EMS2 three kinds of power allocation strategies

3.2.2 单堆系统与双堆MFC系统效率对比

单堆系统和双堆MFC系统在输出相同总功率情况下的累计氢耗曲线如图12所示，其中双堆MFC系统的累计氢耗在整个仿真过程中都低于单堆系统，且随着仿真时间的推移，两者的累计氢耗差异逐步增大。仿真结束时单堆系统总氢耗为123.33g，双堆MFC系统总氢耗为117.92g，后者较前者燃料经济性提高了4.39%。

3.2.3 考虑电堆寿命的仿真对比

30kW双堆MFC中假设2个电堆的RUL曲线不同，如图13所示。

电堆一的RUL曲线较电堆二低，两者的RUL曲线分别为

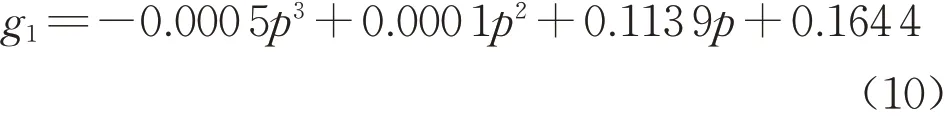
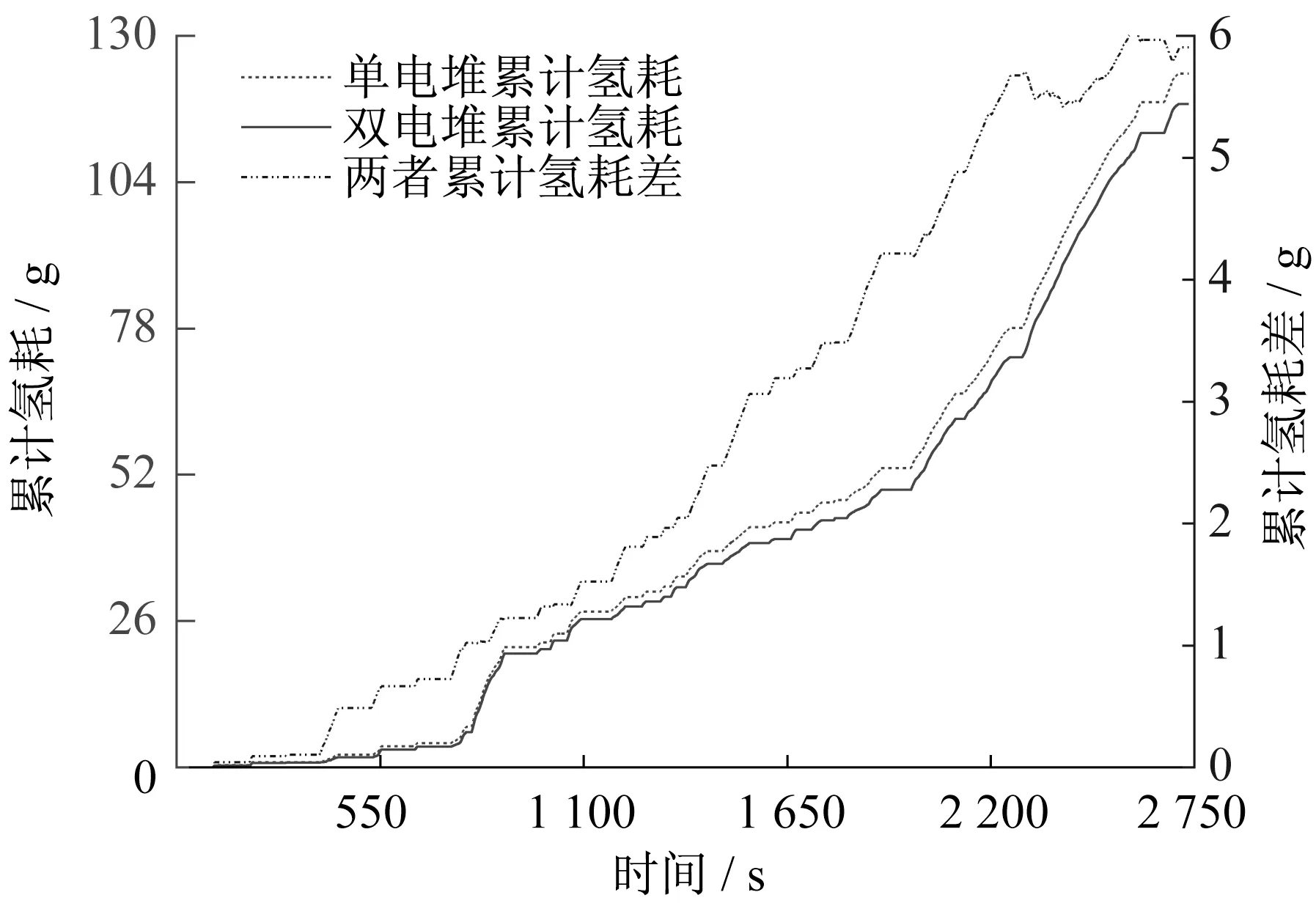
图12 2种燃料电池系统累计氢耗对比Fig.12 Comparison of cumulative hydrogen consumption of two fuel cell systems

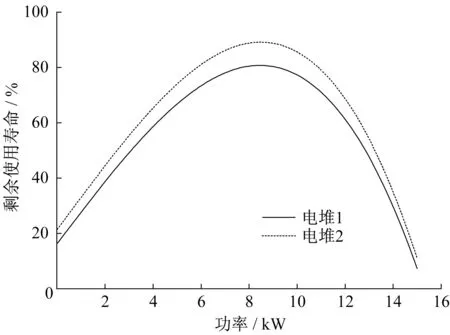
图13 2个15 k W电堆的输出功率-RUL曲线Fig.13 Output power-RUL curves of two 15k W stacks

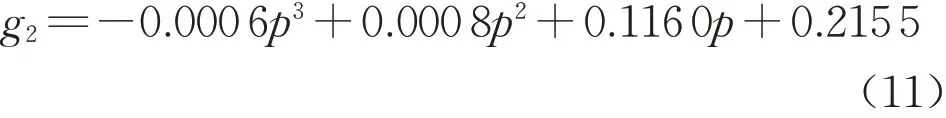
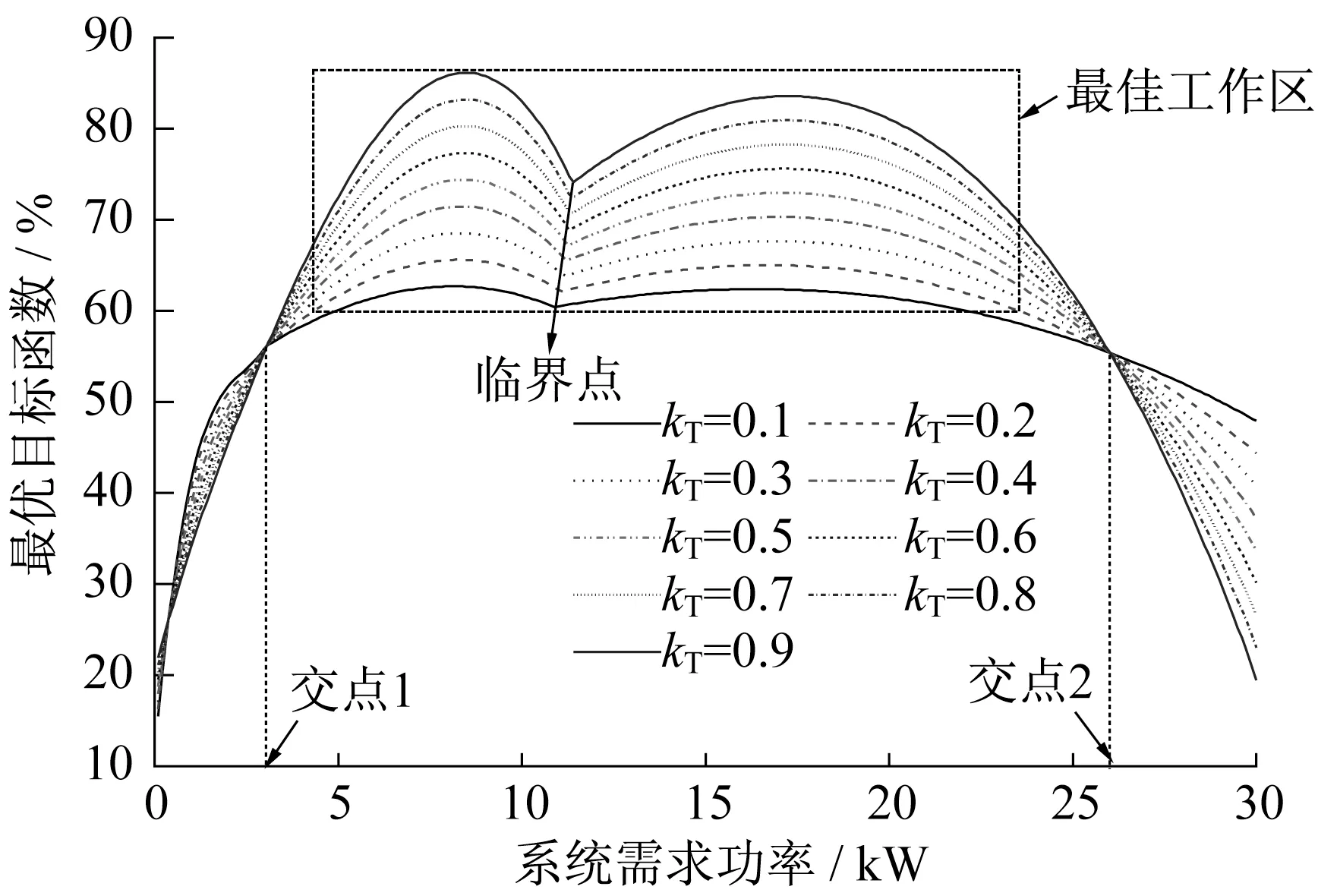
图14 不同寿命因素权重下的目标优化函数Fig.14 Objective optimization function at different life factor weights

根据式（6），得到不同寿命因素权重kT下兼顾效率和寿命的最优目标优化函数曲线，如图14所示。图中各最优目标函数优化曲线有2个交点分别位于Pmfc=3.1kW和Pmfc=26.0kW处。当需求功率位于2个交点的功率值时，最优目标函数值与寿命影响因子无关，当需求功率在交点1左侧或者交点2右侧时，最优目标函数值随着kT增大而减小，当需求功率位于交点1和交点2中间区域时，最优目标函数值随着kT增大而增大。综上，从最优目标函数值大小可以看出，系统的最佳工作区间在交点1和交点2之间，且kT越大，则系统最优目标函数值越大。

4 结论

以车用多堆燃料电池系统为研究对象，对其能量管理与控制策略展开研究。提出了多堆燃料电池系统的二级能量管理概念，第一级能量管理EMS1基于工况识别模型识别整车工况，实现在燃料电池电源和动力电池电源之间的自适应功率分配，仿真结果可节省燃料约1.54%，具有改善燃料经济性的潜力；第二级能量管理EMS2引入了兼顾效率和寿命的目标优化函数，在多堆内分配每个电堆的实时输出功率。以一个30 kW双堆MFC系统为例，进行了仿真研究，研究结果表明，MFC系统相比于传统单堆燃料电池系统，既具有提高系统燃料经济性也具有提高系统寿命性能的潜力。

作者贡献申明：

周 苏：主要贡献为论文指导。

王克勇：主要贡献为论文撰写。

文泽军：主要贡献为论文撰写相关支持。

张 岗：主要贡献为论文撰写相关支持。