汽车起步颤振动力学问题研究综述

吴光强，苑仁飞

（1.同济大学汽车学院，上海201804；2.东京大学生产技术研究所，东京153-8505）

对于配备手动变速器（manual transmission，MT）、双离合自动变速器（dual-clutch transmission，DCT）和电控机械式变速器（automated manual transmission，AMT）的车辆，广泛地使用离合器进行动力传递和切断，分别对应于离合器接合和分离，以应对起步、换挡工况。在起步工况下，由于摩擦的黏滑非线性，使得离合器在滑摩状态下导致传动系统出现剧烈的扭转振动，进而表现为车辆的低频纵向振动，频率范围在5～20Hz之间，称之为汽车起步颤振现象［1-2］，是动力传动系统的典型振动与噪声（noise，vibration and harshness，NVH）问题。拥堵路况使汽车处于停车-起步-再停车的状态，频繁的离合器分离与接合使起步颤振问题更加突出，降低驾乘体验和使用寿命，亟待优化改善，尤其是手动变速器车辆。

汽车起步颤振现象发生在离合器接合过程，与离合器性能密切相关，同时与汽车动力传动系统也密不可分。通过仿真建模和试验分析等研究手段，剖析汽车起步颤振现象的产生机理，分析摩擦非线性因素对其影响规律并提出抑制措施，其中涉及摩擦学、振动力学、非线性系统动力学和控制理论等多个学科领域。围绕汽车起步颤振问题，国内外学者已开展了大量工作并取得了丰富的研究成果。

本文归纳总结汽车起步颤振问题的国内外研究现状和发展趋势。对于整车动力传动系统仿真模型，着重论述了建模方法以及与起步工况密切相关的部件，包括离合器操纵特性、摩擦特性和发动机模型等。针对汽车起步颤振问题，着重从试验研究、产生机理、抑制措施3个方面阐述当前在起步颤振问题研究上取得的研究成果及其不足。最后从研究重点和难点的角度做出总结与展望，为汽车起步颤振动力学问题研究明确方向。

1 整车动力传动系统的动力学模型

汽车起步颤振现象虽是源于离合器接合过程，但表现形式是车身的低频纵向振动，因此需建立整车动力传动系统模型作为现象再现的仿真平台，是研究起步颤振的基础。整车动力传动系统模型由发动机、离合器、变速器、主减速器、差速器、半轴、轮胎和车身等部件组成，用于模拟再现车辆使用过程中的各种现象及效果。对客观对象进行抽象处理，得到整车动力传动系统的动力学模型，所应用建模理论包括集总参数法、多体动力学理论、有限元理论、连续系统振动理论、动态子结构模态综合法等［3］，其中以集总参数法为主。

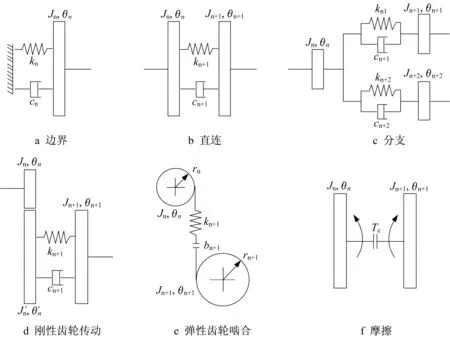
图1 传动系统的扭转有限单元Fig.1 Torsional finite elements for powertrain

集总参数法，又称为集中质量法，将整车动力传动系统的各部件抽象为若干个无弹性的质量块或惯量盘、无质量或惯量的理想弹簧以及黏性阻尼器。按照传动系统的结构特点，由理想弹簧和黏性阻尼器来连接各个质量块或惯量盘，组装成离散系统模型。根据牛顿第二定律或拉格朗日方程建立数学模型，即运动微分方程，配合求解算法即可得到各个质量块或惯量盘的位移、速度、加速度以及传递力或力矩等信息。

Crowther等［4］基于集总参数法提出了单元化建模方法，划分了边界、直连、分支、刚性齿轮传动、弹性齿轮啮合和摩擦等基础模块，并给出了对应的惯量矩阵、刚度矩阵、阻尼矩阵，称为扭转有限单元（torsional finite element），如图1所示。利用扭转有限单元分别组建了配备MT、AT、无级变速器（continuously variable transmission，CVT）的传动系统模型以及用于研究离合器接合过程的动力学模型。

针对离合器接合过程的动力学模型，Idehara等［5］将整车动力传动系统简化为最基础的三自由度扭振模型，如图2所示，并利用牛顿第二定律建立数学模型。图2中J1为离合器主动部分的转动惯量，包括发动机曲轴、飞轮、离合器压盘；J2为离合器从动部分的转动惯量，包括离合器摩擦片、齿轮、传动轴；J3为车轮、整车的等效转动惯量；k1为等效扭转刚度；c1、c3为等效黏性扭转阻尼；Te为发动机扭矩；Tc为离合器摩擦扭矩；Tr为阻力矩。

三自由度扭振模型代表了集总参数法的核心思想，其他的整车动力传动系统模型可在此基础上扩展细化，但对汽车起步颤振现象的模拟效果不够准确，无法与实车试验结果对比。

在上述集总参数建模方法下，大量学者针对不同的研究对象及其问题已开展丰富的建模与分析工作。Couderc等［6］针对传动系统在离合器同步时出现的纵向喘振（shuffle）现象，在考虑离合器扭转减振器的迟滞特性和齿轮的齿侧间隙的基础上，建立了包含传动系统和底盘系统在内的纵-扭动力学模型。对于液力变矩器（torque converter，TC）的锁止离合器在接近闭锁时的颤振现象，金书彝等［7］根据拉格朗日方程建立了闭锁过程的四自由度动力学模型，并利用李雅普诺夫（Lyapunov）第二方法推导了发生颤振的必要条件。

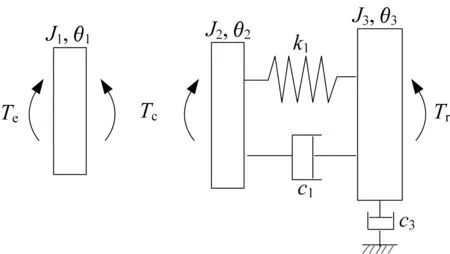
图2 整车动力传动系统的三自由度扭振模型Fig.2 Three DOF torsional vibration model of vehicle powertrain

轮胎与路面间的地面纵向力构建了传动系统的扭转运动和车身的纵向运动之间的耦合关系。轮胎纵向力和车身纵向加速度与车身的俯仰运动密切相关，也构建了车身的纵向运动和垂向运动之间的耦合关系。车轮的垂向动载荷与轮胎地面纵向力密切相关，使车身的垂向振动也影响着纵向运动和传动系统的扭转运动。以上构成了扭转、纵向、垂向运动相互之间的闭环耦合关系，如图3所示。

栾文博［8］在传动系统分支扭转模型的基础上，并假设前、后轴的左、右车轮垂向载荷一致，建立了26自由度的车辆扭-纵-垂振动耦合模型，分析汽车起步颤振现象的影响因素。Lee等［9］针对齿轮传动系统的弯-扭耦合振动力学模型的特点，将有限元理论和集总参数法相结合建立了传动系弯-扭耦合模型。对于不同研究对象及其NVH问题的仿真建模工作，需具体问题具体分析，以模拟再现问题特征为核心要求，在模型精度和计算效率之间权衡，根据各自特点得到适合模拟再现NVH问题的仿真模型。

2 离合器摩擦扭矩的建模工作

汽车起步颤振现象源于离合器的滑摩状态，摩擦是一种复杂的非线性物理现象，表现为在具有相对运动或有相对运动趋势的接触面间的摩擦力，摩擦力本身因受诸多因素影响，如温度、材料属性、作用力、接触粗糙度、速度等，表现出强烈的不稳定性及非线性特征。摩擦广泛存在于机械系统中，对系统的振动特性有着重要的影响，离合器摩擦片的摩擦特性是自动变速器起步控制策略制定及相关零部件设计的重要参考依据，摩擦特性的精确数学模型有利于提高自动离合器的控制性能。因此，在汽车起步颤振的仿真模型中，需着重关注与离合器摩擦特性相关的建模工作，主要涉及摩擦片的摩擦系数、离合器夹紧力等参数，离合器摩擦扭矩Tc的计算表达式为

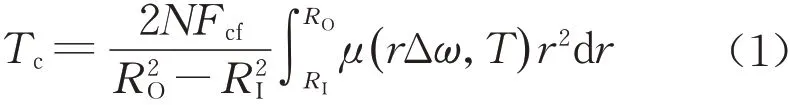
式中，Fcf为离合器夹紧力；μ(rΔω，T)为摩擦系数，与离合器的相对速度、摩擦片温度相关；N为摩擦面个数；RO为摩擦片的外半径；RI为摩擦片的内半径。

2.1 离合器操纵特性

在离合器从动盘的结构中有2个关键的弹性组件：①周向弹性组件。扭转减振器，安装在从动盘轮毂和摩擦片之间，衰减传动系统的扭转振动；②轴向弹性组件。膜片弹簧-波形片-传动片组合，缓和飞轮-摩擦片-压盘间的正压力波动和冲击，使离合器夹紧力平稳地增长。

波形片的轴向压缩特性表现为压紧力随位移的增大先缓慢增大后急剧增大，由波形片的变形量即可得到对应离合器夹紧力。Cappetti等［10］针对波形片轴向压缩特性，选取波形高度、厚度、孔径和波峰数4个设计参数进行了灵敏度分析，有限元仿真结果表明波形高度和厚度是其主要影响因素，并分析了温度对轴向压缩特性的影响。栾文博等［11］考虑到波形片的非线性轴向压缩特性，对其实验数据进行插值拟合，建立了压盘行程（即波形片变形量）与离合器夹紧力之间的对应关系，并控制压盘接合行程及接合速度来实现发动机恒转速起步，但在电控离合器中对分离轴承行程的控制更具现实意义。

膜片弹簧位于压盘和离合器盖之间，建起了分离轴承和压盘之间的力或位移传递关系，Almen和Laszlo［12］在铁摩辛柯（Timoshenko SP）假设下，即在轴向载荷的作用下碟形弹簧的矩形子午截面只是绕某一中性点转动，而矩形截面本身没有变形，推导了膜片弹簧压缩特性的理论计算A-L法，计算结果表明：随变形量的逐渐增大，载荷则是先增大随后减小再次增大。史佳薇等［13］基于膜片弹簧的A-L法，选取碟形弹簧外半径、内截锥高度、压盘作用半径、支撑环作用半径4个结构参数，分析了它们对压缩特性中的凹凸点位置和载荷的影响规律。林恩等［14］考虑了膜片弹簧与压盘和支撑环之间的接触和摩擦，建立了膜片弹簧大端受载的精确有限元模型，对其力学特性进行分析，与试验结果对比表明：有限元分析结果比A-L法计算结果更加精确，能够表达加载-卸载过程的迟滞特性。

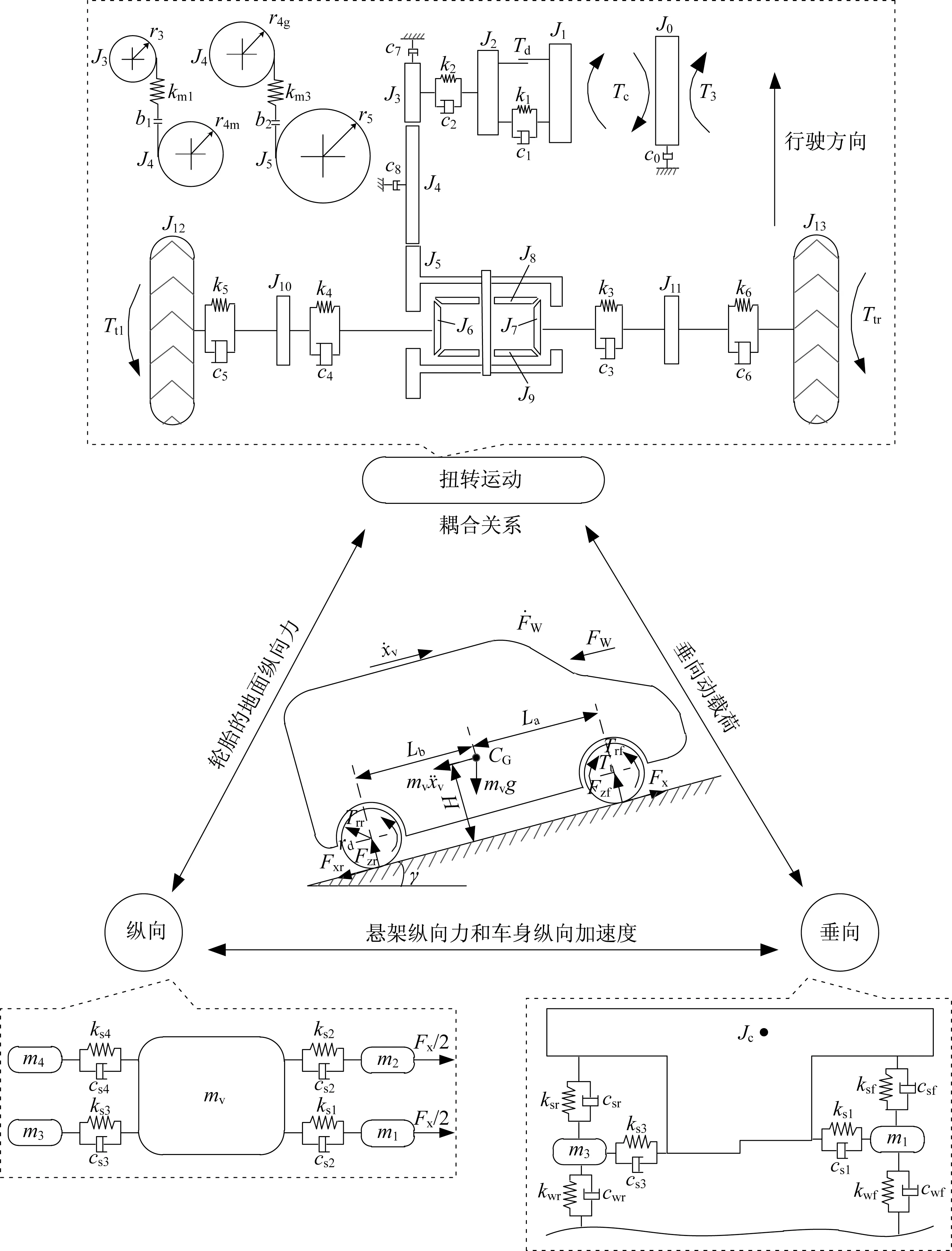
图3 扭-纵-垂向耦合的整车动力传动系统模型Fig.3 Torsion-longitudinal-vertical coupling of vehicle powertrain model

对电控离合器的位置或速度控制来说，还需进一步推导分离轴承行程与离合器摩擦扭矩的对应关系。对于干式离合器的夹紧力，涉及膜片弹簧、波形片、传动片3个弹性部件的轴向压缩特性。Yuan等［15］根据膜片弹簧、波形片和传动片的轴向压缩特性及其三者之间的受力关系建立了分离轴承行程和离合器夹紧力之间的非线性关系。

2.2 摩擦特性

计算离合器摩擦扭矩的另一个关键参数是摩擦系数，是接触面间的摩擦力与垂直于接触面的压力之比，其与滑摩速度、温度、夹紧力、磨损和材料成分等因素相关。对于离合器接合过程，离合器夹紧力逐步增大，离合器主、从动部分的相对速度逐步减小，由摩擦生热使摩擦片温度逐步升高。

对于干式离合器，Bostwick等［16］针对重型汽车用的陶瓷基摩擦材料，通过台架试验研究了摩擦系数与滑摩速度之间的关系，在滑摩速度从1 000r·min-1降至零的过程中，摩擦系数多次出现随滑摩速度的增大而减小的现象，称为负斜率特性，尤其是在低滑摩速度（0～100 r·min-1）和中滑摩速度（400～700 r·min-1）时，并表明负斜率特性使传动系统倾向于发生起步颤振现象。Li等［17］研究了离心式离合器在接合过程中的颤振问题，试验分析了18种摩擦材料样本的摩擦特性，包括动静摩擦力矩之比、摩擦系数相对滑摩速度的斜率等特性，试验结果表明不同摩擦材料的摩擦系数随滑摩速度的变化率皆为负值，即负斜率特性，并且动静摩擦力矩之比皆大于1.15。Lin等［18］在建立干式离合器的摩擦扭矩模型时，对编号为Schaeffler B-8805的摩擦材料进行了多因素交叉的64组台架实验，基于实验数据所建立的摩擦系数模型中考虑了温度、滑摩速度和夹紧力3个因素，结果表明摩擦系数随滑摩速度的增大而减小，随温度的增大则先增大后减小（拐点在200°C左右），随夹紧力的增大而减小。Hoić等［19］设计了销盘式摩擦磨损试验机（pin-on-disc tribometer），可直接控制其夹紧力、滑摩速度和温度，用于测量不同摩擦材料的摩擦系数、颤振倾向性和磨损率，试验结果表明：在不同夹紧力和磨损率下，摩擦材料B的摩擦系数与滑摩速度之间皆表现为负斜率，对起步颤振现象的发生更加倾向，摩擦材料A则与之相反。

对于湿式离合器，Iqbal等［20］指出了湿摩擦由Stribeck效应和黏滞效应两部分组成，利用SAE#2试验装置测试了湿式离合器的压力、转速、转矩信号，试验数据显示：在低速滑摩区，摩擦力矩以Stribeck效应为主，即负斜率特性；在高速滑摩区，摩擦力矩以黏滞效应为主，即正斜率特性。Ost等［21］以湿式离合器用纸基摩擦材料为研究对象进行了摩擦特性试验，试验表明：摩擦系数还受循环次数和夹紧力的影响，随循环次数的增大而减小，且愈来不稳定；随夹紧力的增大而减小，并渐进趋于平稳。

对于起步工况来说，滑摩速度必然从怠速逐渐降至零，其是影响摩擦系数的主要因素，发动机转速是计算滑摩速度的因素之一，因此对发动机模型提出了较高的精度要求。

2.3 发动机扭矩

发动机为车辆提供动力的同时也为传动系统引入了扭转激励，对整车性能具有重要影响，针对不同的研究课题，发动机模型方法可分为两大类：试验法和解析法。

试验法：通过拟合发动机万有特性的台架试验数据得到MAP图，对转速和节气门开度进行数值插值即可得到相应的发动机扭矩，称为稳态发动机模型。逄淑一等［22］针对油门突变所导致的发动机动态特性与稳态特性不一致问题，在稳态发动机模型的基础上建立了一阶滞后环节的动态修正模型。现有的车辆动力学商业软件中同样建立了基于MAP图的稳态发动机模型，如Carsim、ADAMS/Car和AVL/Cruise等。稳态发动机模型适用于整车动力学分析与控制方面的研究课题，但在振动与噪声方面的研究课题中不能模拟扭振成分。可在发动机稳态扭矩的基础上加入傅里叶（Fourier）级数来模拟发动机的扭转振动［23］，一般表达式为

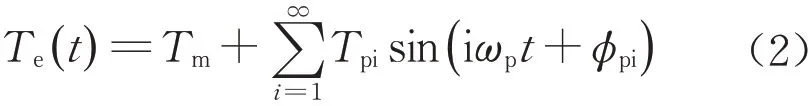
式中，Tm为发动机的稳态扭矩；ωp为点火圆频率，对应于发动机转速并与气缸数量有关；Tpi为发动机波动力矩的第i阶分量的幅值；φpi为发动机波动力矩的第i阶分量的相位，根据不同的精度需求，可选择不同的阶数。

解析法：基于曲柄连杆机构的动力学和运动学分析，如图4所示，考虑不同节气门开度下的缸内气体燃烧压力以及活塞往复惯性力矩，计算得到不同转速和节气门开度下的发动机瞬态扭矩。

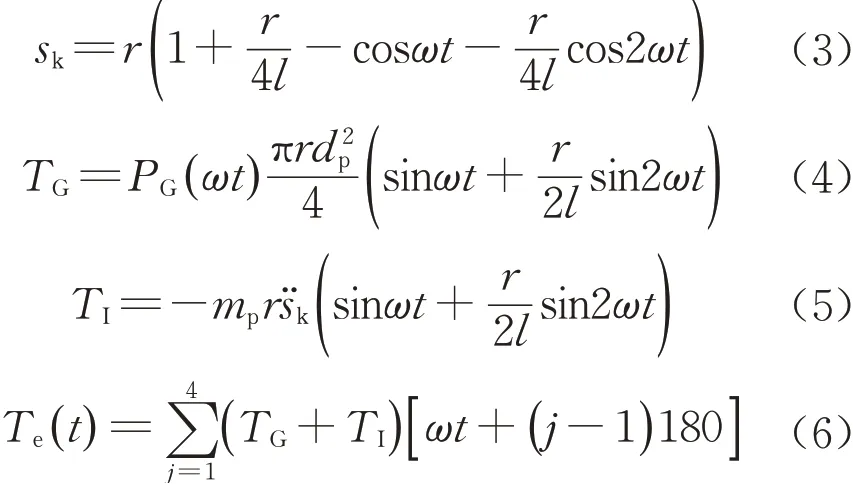
式中，l为连杆长度；r为曲柄半径；ω为曲轴角速度；dp为活塞直径；mp为活塞、活塞环、活塞销及部分连杆的等效往复质量；PG(ωt)为随曲轴转角变化的缸内气体燃烧压强；j为气缸编号。

缸内气体燃烧压力可由试验或者数值模型获得，Desbazeille等［24］以韦伯（Wiebe）燃烧模型为基础，根据温度、压强和体积之间的热力学关系，推导了缸内气体压力的理论公式，与点火延迟、燃烧持续时间等相关。已有成熟商业软件，如GT-Power、AVL/Boost、AMEsim等，以一维流体动力学为基础，模拟发动机的喷油、配气、正时、燃烧等一系列过程，可方便地控制转速和节气门开度（与MATLAB/Simulink软件协同仿真），通过缸内气体燃烧压力、往复惯性力矩和摩擦力矩等计算发动机瞬态扭矩。

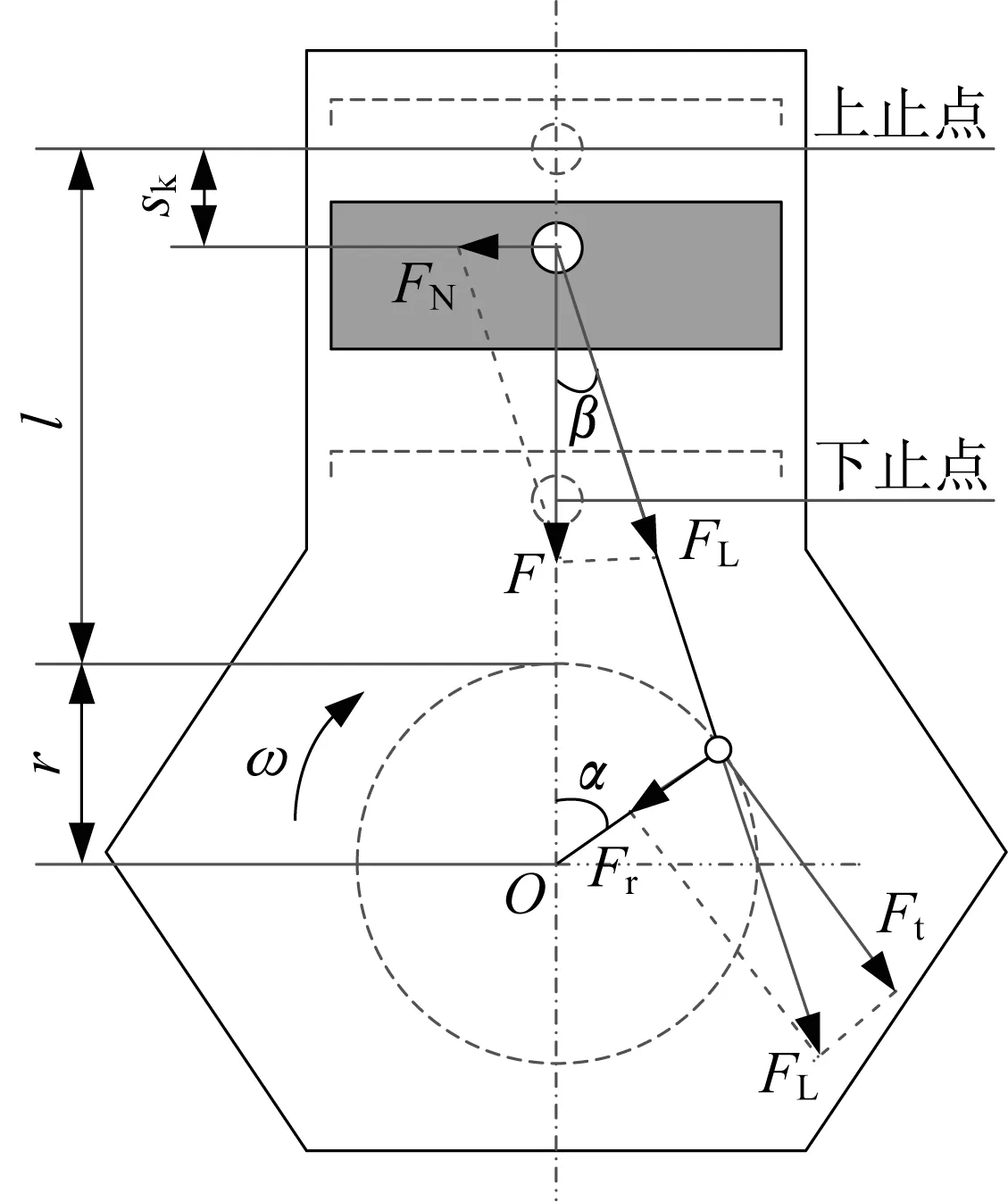
图4 发动机的动力学和运动学分析Fig.4 Kinematic characteristics and force analysis of engine

综合可知，总结了整车动力传动系统的建模方法，针对汽车起步颤振现象着重介绍了离合器操纵特性、摩擦特性和发动机模型，在仿真模型的基础上可深入展开与起步颤振相关的研究工作。

3 汽车起步颤振问题的研究现状

对于解决NVH问题的一般思路：首先设计试验方案，数据采集并辨识现象特征；然后建立试验对象的仿真模型并试验数据验证，基于仿真模型剖析现象发生机理及影响因素；最后从破坏机理条件的角度，提出相应的抑制措施并试验验证。因此，论述汽车起步颤振现象的国内外研究现状及发展趋势，着重从起步颤振的试验研究、产生机理、抑制措施3个方面展开，如表1所列。

表1 汽车起步颤振问题的研究内容Tab.1 Research content of vehicle start-up judder

3.1 起步颤振的试验研究

为分析汽车起步颤振现象的特性，国内外多家企业、研究机构及高校开展了试验研究，用于辨识现象特征、仿真模型验证及抑制措施的试验验证，可分为台架试验和整车试验。

（1）台架试验。台架试验排除了其他干扰激励，可针对性地研究与离合器相关的起步颤振现象，缩短产品的测试周期。试验台架围绕离合器接合与分离而搭建，主要由驱动电机、飞轮、离合器总成、等效负载盘、伺服电机和传感器等部件组成，模拟起步工况并采集能够反映颤振现象的各种信号。在台架试验中可采集传动轴扭矩、等效负载盘转速、夹紧力等信号来反映离合器接合过程的颤振现象，试验结果表明轴系不对中或摩擦面不平度会导致夹紧力波动，其激励频率与相对速度和摩擦盘转速相关［25］。还可测试不同摩擦材料在不同温度下的颤振现象，试验结果表明在低温（60°C）和高温（250°C）时更易发生颤振现象［26］。与整车试验相比，缺乏对汽车起步颤振现象的主观评价。

（2）整车试验。整车试验是研究车辆实际使用工况下的NVH问题的重要手段之一。根据汽车起步颤振现象的特征设计试验方案，包括挡位、油门、离合器接合速度等信息的试验工况等；布置传感器采集各类振动与噪声信号，主要是发动机转速、变速器转速、驾驶员座椅导轨的纵向加速度等；通过时频分析等数据处理后辨识汽车起步颤振的特征频率，并结合传动系统的固有频率分析颤振机理［27］。

试验研究NVH问题的特征测试、验证优化或解决方案都会涉及对汽车起步颤振现象的主、客观评价。Gregori等［28］通过多元统计方法分析了台架试验的摩擦材料斜率特性与整车试验的颤振主观评价之间的相关性，表明负斜率特征越明显（负斜率小于—0.004s·m-1时），起步颤振的主观评价则越不可接受（纵向加速度大于2.1m·s-2时主观评价不可接受）。

数据处理方法是试验分析的重要手段，在时域、频域、时频域和阶次域内，从原始实测数据中多维度地挖掘重要信息来反映现象特征。由于发生起步颤振时的转速或加速度信号皆是非平稳的，快速傅里叶变换的频域分析不能够定位频率的时间信息，因此需短时傅里叶变换（short time Fourier transform，STFT）等时频分析方法，同时在时域和频域内联合观察信号的能量分布情况，方便辨识起步颤振的特征频率。

综合可知，台架试验和整车试验的各自侧重点不同，台架试验的试验数据可为离合器摩擦特性的建模提供详细的参数，而整车试验更便于观察和感受起步颤振现象，试验数据可用于辨识特征、计算客观指标、进行主观评价、仿真模型调试与验证等，使仿真结果与试验结果在时频域内皆有较好的一致性，为颤振机理研究奠定基础。

3.2 起步颤振的产生机理

试验研究明确了汽车起步颤振现象的特征，还需通过机理研究来剖析现象发生的推演过程，揭示内在规律性，总结影响现象的本质因素。汽车起步工况伴随着离合器的接合过程，其中涉及到摩擦副的滑摩和夹紧力的施加，使飞轮与离合器从动盘的转速趋于一致。因此，关于汽车起步颤振的机理研究主要集中在摩擦自激振动和强迫振动两方面。

（1）摩擦自激振动。自激振动系统是非保守非线性自治系统，依靠自身运动状态的内在反馈机制自主地从恒定能源中汲取能量，得以周期性地补充耗散能量，是自然界和工程中广泛存在的一类振动形式。自激振动的2个发生条件：第一，系统在平衡点附近的不稳定性；第二，迫使系统的工作点略微偏离平衡点的外界扰动。研究摩擦自激振动机理的典型例子是单自由度传动带-滑块模型，由恒速传动带与滑块之间的摩擦力驱动滑块运动，其中摩擦特性至关重要。

离合器的滑摩过程对整车动力传动系统引入了不稳定因素，分析离合器的摩擦特性有助于深入地理解汽车起步颤振现象的产生机理。在三自由度扭振模型（图2）中，描述离合器从动盘的运动微分方程为

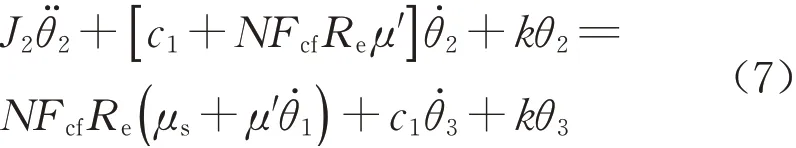
式中，μ′为摩擦系数随相对速度的变化率，当μ′小于零（即摩擦系数随相对速度的增大而减小，表现为负斜率特性）且使式（7）的阻尼系数也小于零时，则使系统发散并诱发颤振。因此，从摩擦自激振动的角度，摩擦系数的负斜率特性为系统导入了负阻尼，是起步颤振发生的必要条件。通过分析系统稳定性的临界条件，或者对比不同斜率特性下的离合器从动盘转速波动，已有文献工作证明了上述观点，但只是说明了摩擦特性的负斜率与起步颤振之间的因果关系，起步颤振是系统出现负阻尼时的表现形式，但皆未深入剖析负阻尼的导入过程及其作用机制，这对解释起步颤振的产生机理及后续抑制措施不利。基于试验验证的整车动力传动系统仿真模型，Yuan等［29］指出：由Stribeck效应的负斜率特性所构成的闭环正反馈过程，即是负阻尼的导入机制，其逐渐加剧离合器从动盘的转速波动，并说明了起步颤振的特征频率与系统固有特性之间的关系。

（2）强迫振动。除了摩擦自激振动之外，强迫振动是汽车起步颤振现象的另一产生机理，主要与离合器夹紧力的激励相关，进一步影响到离合器摩擦扭矩。当激励频率与传动系统的固有频率接近或相等时，系统则发生共振，表现为起步颤振现象。强迫振动的激励源主要来自：①制造与安装超差，如轴系不对中、飞轮和压盘的端面跳动、分离轴承倾斜等；②外部激励，如离合器操纵力或油压的波动等；③热效应，如非均匀热变形等。

Kato等［30］分析了影响离合器摩擦扭矩波动的因素，包括与旋转部件相关的压盘倾斜、波形片高度等，试验和仿真结果表明纵向加速度随两者的增大而增大。Yang等［31］对比分析了摩擦面间的油压波动和发动机输出扭矩的谐次激励对起步颤振的影响，油压和发动机扭矩的波动频率与系统固有频率接近或相等时，起步颤振现象明显。Menday等［32］研究了颤振问题车辆的离合器摩擦片在内、外半径处发现的热点，研究表明热点是由于离合器夹紧力的分布不均匀，主要是在高温度梯度下，热量快速累积并发生局部变形和环形焦烧，从而影响摩擦扭矩。

综合可知，不管是摩擦自激振动机理还是强迫振动机理，最为关键的因素是起步过程中的离合器摩擦扭矩。因此，对于汽车颤振现象的机理研究，不应孤立地研究单一机理，而是应当从两者相辅相成的角度来理解起步颤振的推演过程并总结其产生机理。

3.3 起步颤振的抑制措施

研究NVH问题是为了抑制或减缓所不希望的振动与噪声现象。在汽车起步颤振机理和影响因素的基础上提出相应的抑制措施，主要从结构与参数优化和主动控制策略两方面展开起步颤振的抑制研究。

（1）影响因素的参数优化。从摩擦自激振动机理的角度，需改善离合器摩擦片的斜率特性，减小负斜率的绝对值，或为正斜率，缩小静、动摩擦系数之差。从强迫振动机理的角度，需缓和离合器夹紧力的冲击、波动等情况，避免其频率与传动系统固有频率接近时的共振，适当降低波动片的轴向压缩刚度。除此之外，从振动系统的角度，适当增大系统阻尼，提高扭转刚度，加大从动部分转动惯量，有助于抑制起步颤振强度，但会受到其他工况下振动问题的掣肘。

Zhang等［33］研究了不同斜率特性、系统阻尼、系统刚度、最大静摩擦系数、齿侧间隙、油压波动和发动机扭振等因素对起步颤振的影响规律，从传动系统的结构参数设计及优化的角度，为抑制或减缓汽车起步颤振现象提供了理论参考。Li等［34］通过改善波形片的结构，增大主波高度和过渡半径可使其轴向压缩特性更加平缓，整车试验结果验证了这一抑制措施的有效性。对于液力变矩器中的锁止离合器，Zhao等［35］表明合适的自动传动油液（automatic transmission fluid，ATF）可使摩擦特性表现为正斜率，具有抗颤抖性能，此外Ryu等［36］提出了在作动活塞上加装动力吸振器来抑制颤振问题。

从机理角度不难找到抑制汽车起步颤振的方法，但是改变离合器的摩擦特性在实践中却是困难而昂贵的，尤其是干式离合器。同时传动系统的参数调整还需考虑动力性、耐久性等其他性能要求，比如接合时间、滑摩功、换挡冲击等问题。

（2）颤振抑制的主动控制。随着AMT、DCT等自动变速器的广泛使用，离合器操纵的自动化控制是关键技术之一。鉴于分离轴承行程或油压与离合器夹紧力之间的对应关系，分离轴承行程或油压可作为一个方便的可控变量来实现对离合器摩擦扭矩的实时调控，以滑摩功、起步冲击度等性能为最优指标，利用最优控制、鲁棒控制、模糊控制等控制理论，达到车辆平稳起步的效果。

为使离合器接合过程既快又平稳，Naus等［37］设计了鲁棒稳定的反馈控制器，以离合器夹紧力为控制变量，建立了考虑摄动参数的系统模型，包括外部干扰、摩擦特性、参数误差等不确定性参数，并在硬件在环（hardware in the loop，HIL）仿真平台上验证了控制器对抑制起步颤振的有效性。Pisaturo等［38］应用模型预测控制（model predictive control，MPC）研究了AMT在起步工况下的性能表现，设定了输入变量和输出变量的约束条件，由于在同步时刻前后系统模型的自由度不连续，针对滑摩阶段（五自由度）和同步阶段（四自由度）设计了不同参数的多约束MPC控制器，对比了有无约束条件时的控制效果。

Lu等［39］将最优控制理论应用在自动离合器上，构建哈密尔顿（Hamilton）函数时考虑了滑摩功和起步冲击度等因素，以发动机扭矩和离合器摩擦扭矩为控制变量，利用极值原理求解了离合器的最优接合规律，结果表明滑摩功和起步冲击度的加权系数之比可作为主要的调整参数来代表不同的驾驶员起步意图，包括慢速起步、中速起步和快速起步，并且冲击度皆满足设定要求。

杨伟斌等［40］在DCT的起步模糊控制中，用加速踏板开度及其变化率来辨识驾驶员起步意图，用起步意图、转速比（发动机转速减去离合器从动盘转速再除以发动机转速）和转速差来决定离合器接合速度，基于均匀设计方法获得了隶属度函数组合，通过仿真验证了所指定控制策略的合理性。

综合可知，上述各类控制策略的本质皆是为了控制离合器摩擦扭矩来实现起步颤振的抑制效果，但是所建模型过于简单或者基于不合理的假设，其中变速器输入轴转速的仿真结果与实车试验结果差异较大，不能真实地反映出由离合器接合所引起的起步颤振问题。在滑摩速度及其变化率的计算中，控制模型并未考虑发动机固有的转速波动情况，这与实际情况不符，并且诸多控制策略缺乏实车试验验证。因此，应当从汽车起步颤振的产生机理入手，通过主动控制或结构优化等手段来阻断其产生条件，进而达到抑制起步颤振的效果。

4 总结与展望

总结了汽车起步颤振动力学问题研究现状，重点分析了起步颤振在试验研究、产生机理和抑制措施等方面的研究成果及其不足，建议今后的研究应主要集中在以下几个方面：

（1）模拟汽车起步颤振现象的特征。建立整车动力传动系统模型，需着重关注离合器摩擦扭矩，包括发动机瞬态扭矩、离合器操纵特性、动态摩擦模型等，同时存在其他的强非线性因素，比如轮胎的非线性附着特性、斜齿轮的时变啮合刚度及齿侧间隙。在反映起步颤振特征上，模型仿真结果需与实车试验结果保持较好的一致性。

（2）剖析汽车起步颤振现象的产生机理。基于整车动力传动系统模型，从摩擦特性和激励频率切入，分析摩擦自激振动和强迫振动对起步颤振的作用机理，解释负阻尼的导入过程及影响因素，并验证起步颤振机理的有效性和正确性。

（3）机理导向的颤振抑制措施。以分离轴承位置或油压为控制变量，设计能够破坏起步颤振机理的控制策略，以达到抑制起步颤振的效果，并通过电控离合器系统的实车试验来验证控制策略的可行性。

作者贡献申明：

吴光强：确定总体架构，甄别相关重要文献，负责指导论文并撰写纲要。

苑仁飞：系统查询、总结相关文献，撰写论文主要内容，与第一作者合作完善。