混凝土/花岗岩界面Ⅰ-Ⅱ复合型动态断裂试验研究

马振洲， 钟 红， 陈育志， 王小乐

(1.河北渤海投资集团有限公司，河北 沧州 061113；2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100048； 3.金陵科技学院 建筑工程学院，南京 211169)

工程领域中的裂缝问题一直是研究坝体安全的焦点问题，裂缝是否发展、如何发展将直接关系到坝体溃决甚至民众安全。工程实际中的坝体多建立在岩基之上，混凝土与岩石的交接处是结构的薄弱部位，微裂缝往往在此产生并多处于复合应力环境中。近年来，针对Ⅰ-Ⅱ复合型混凝土-岩石界面断裂的研究已开展了许多，主要结论涉及如下：确定合适的评价准则可以有效判断界面裂缝起裂-扩展问题[1-6]，如已提出的临界应力强度因子评价准则、最大拉应力(应变)准则、界面椭圆型断裂准则等；加载模态比、界面粗糙度、缝高比等单一特殊变量的改变对断裂韧度、应变能释放率等重要断裂参量的影响比较显著[7-9]。上述成果虽多维度研究了混凝土/岩石的界面断裂特性，但均表现在静态特征范畴，针对界面断裂的动态加载性能研究还鲜有报道。

坝体在运行阶段除了承受静载作用之外，还可能遭遇地震、动水压力等外界动荷载的影响，对结构的安全性评价往往也由其在动荷载作用下所表现出的性质决定。外界荷载与应变率存在一定的对应范围[10]，可由相应范围的应变率描述动力荷载。调研发现虽然已有关于界面材料在动荷载作用下的特性研究，如碳-环氧结构、混凝土-FRP片材结构等，但对于工程上混凝土/岩石界面应变率效应问题的研究则很少被开展，目前仅发现王瑶等[11-12]对砂浆-花岗岩界面试件进行了率相关性试验以及钟红等[13]开展的混凝土-花岗岩界面轴拉Ⅰ型动态断裂性能试验，故有必要拓展对混凝土/岩石界面在动态特性方面的研究。基于此，本论文以建在岩基上的混凝土结构的抗震性能为背景，对混凝土/花岗岩复合试件进行地震特征应变率范围的四点剪切试验，研究混凝土/花岗岩界面在复合型应力条件下的应变率特性，从而为工程实际中混凝土/岩石界面结构的抗震安全评价提供试验参考。

1 试验概况

1.1 试件制备

本试验试件形式采用500 mm×100 mm×100 mm的混凝土/花岗岩复合型试件，在交界面部位预制一深度为30 mm的裂缝，如图1所示。试件制备方式如下：首先对经加工好的花岗岩一侧进行人工切槽用以保证两种母材的结合性，切割深度为3 mm；然后在切割面下方粘贴两层100 mm×30 mm的薄膜片以隔离母材形成预制裂缝；最后按照混凝土(配合比为水泥∶水∶砂子∶石子=1∶0.55∶3.41∶1.83)制备的标准程序进行复合试件的成型-养护(因试验设备问题，复合试件在养护7个月后取出进行试验)工作。

图1 四点剪切梁(mm)Fig.1 Four-point shear beam(mm)

1.2 试验方案

试验考虑10-5s-1，10-4s-1,10-3s-1和10-2s-1四种应变率，利用美国MTS-322液压伺服试验机对混凝土/花岗岩复合试件在每种应变率下进行四点剪切试验，试件及监测设备的安装形式如图2所示，其中，裂缝张开位移和裂缝剪切位移通过引伸计监测；两加载点挠度由LVDT监测；荷载经试验机系统采集。通过调整混凝土和花岗岩二者的相对长度，使模态角均匀分布。经计算，将每种应变率下的试验分为三组模态工况，即模态角ψ(ψ=arctan(τxy/σyy)=arctan(K2/K1)，以正值进行表示，在进行模态比相关性分析时通过模态角来表征)分别为21.8°，41.7°和60.3°，试验方案如表1所示。

图2 试件的安装方式Fig.2 Installation method of composite specimen

表1 试验方案Tab.1 Test scheme

加载过程由试验机自带的夹式引伸计监测到裂缝张开位移CMOD的变化量进行控制。动态断裂试验同时设计了三点弯曲试验和四点剪切试验，本试验采用了三点弯曲试验的控制速率[14]，由三点弯曲梁受力时的理想变形确定。假定如图3所示的均质梁在裂缝a未扩展时绕支座旋转[15]，支座距试件中心L/2，受荷载P作用，加载点位移的变化量为δ，试件绕支座旋转角度为θ，则裂缝张开位移CMOD与加载点位移δ的关系见式(1)，而加载点位移变化量可由应变关系得到，故而可获得每种应变率下裂缝张开位移的控制速率。

图3 三点弯曲梁变形图Fig.3 Three-point bending beam deformation diagram

(1)

2 试验结果

2.1 P-CMD曲线

四点剪切试验中混凝土/花岗岩复合试件的断裂形式呈现出一致性，即断裂位置均发生在花岗岩与混凝土的交界面处。将试验过程中采集到的荷载P与裂缝口位移CMD(CMOD为裂缝张开位移；CMSD为裂缝剪切位移)的关系曲线如图4所示，可以发现，三种模态工况试验在应变率为10-5s-1和10-4s-1时均获得了完整的P-CMD曲线(多数文献在准静态情况下进行四点剪切试验，以加载点位移控制试验过程，仅得到试验曲线的上升段)；在应变率为10-3s-1和10-2s-1时，由于“加载-断裂”过程极短，峰值以后的数据点呈直线下降，明显偏离试验曲线的趋势，视为无效点(试件已发生失稳破坏)，仅在图中展示有效的峰前段部分。随着模态角的增加，图4(a)～图4(c)各对应应变率下的峰值荷载均有不同程度的提高。比较裂缝口位移发现，每种模态工况的复合试件在断裂前的初始刚度基本一致，且同一时刻的CMOD的值均大于CMSD的值。

图4 P-CMD曲线Fig.4 The P-CMOD curves

2.2 断裂韧度的椭圆准则

利用试验-数模耦合方式计算Ⅰ-Ⅱ复合型应力强度因子。应力强度因子K1和K2可通过对界面力学定义的裂缝面开口位移表达式[16]进行变换求出

(2)

式中：δx,δy分别为裂缝剪切位移和裂缝张开位移；K1,K2分别为界面张开型应力强度因子和界面剪切型应力强度因子；κ，μ分别为材料的卡帕参数和剪切模量；下标1,2为两种材料号；ε为界面裂纹的振荡因子；r为裂缝翼缘到裂尖的距离；L为特征长度(计算时取L为预制裂缝长度的2倍)。

采用ANSYS软件建立混凝土/花岗岩复合试件的有限元模型，如图5所示，材料参数经试验测得，如表2所示。将试验获得的荷载时程曲线作为试件有限元动力时程分析的输入，通过逐步求解动力方程获得在加载过程中试件的响应时程，在此基础上计算每一时刻裂尖处的应力强度因子。以模态角为21.8°、应变率为10-2s-1的工况作为示例，图6中展示了一个试件在试验中测得的荷载-时间曲线，以及Ⅰ型、Ⅱ型应力强度因子时程曲线。

图5 有限元模型Fig.5 Finite element model

表2 材料力学参数Tab.2 Mechanical parameters

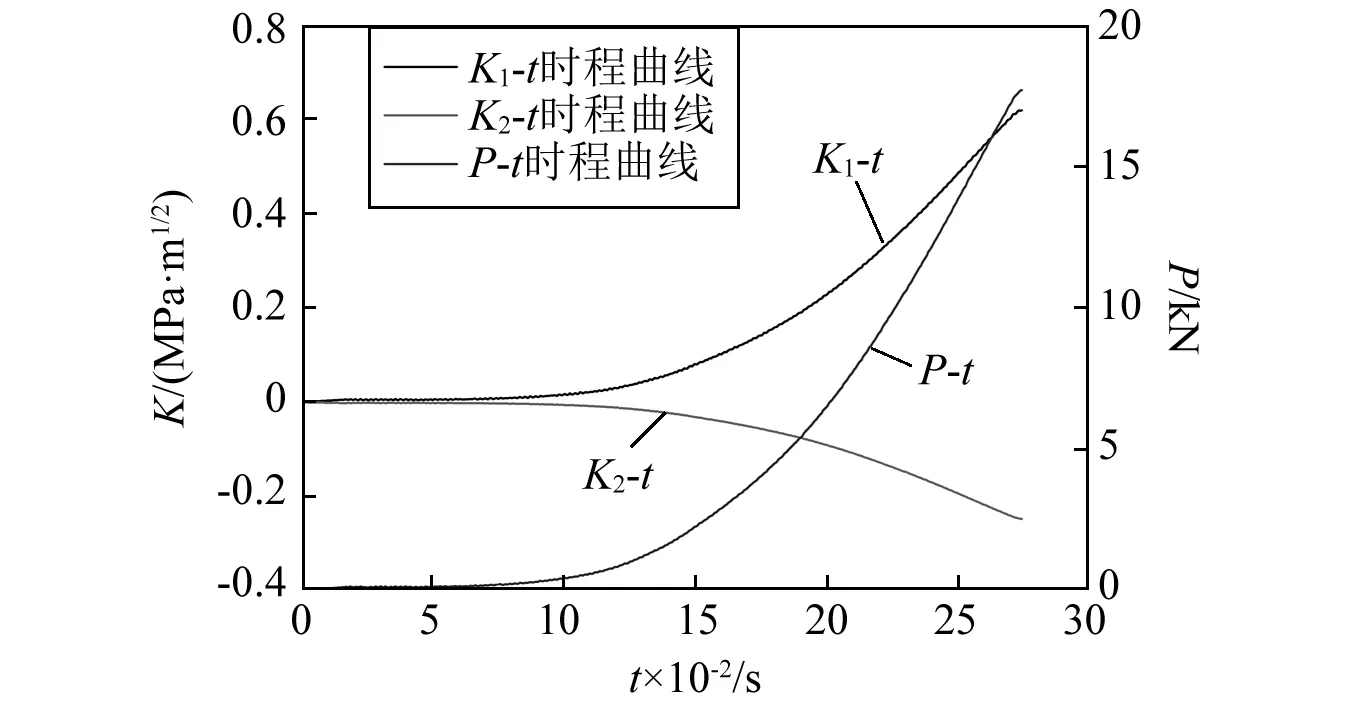
图6 Ⅰ-Ⅱ型应力强度因子时程曲线Fig.6 Mode I-II stress intensity factor time history curves

图7 断裂韧度Fig.7 Fracture toughness

2.3 断裂韧度的率相关性及模态比相关性分析

根据表3数据结果，以Ⅰ型和Ⅱ型断裂韧度的平均值进行分析，断裂韧度和应变率(以目标应变率与基准应变率之比的对数值表示)的关系如图8所示，可以发现，三种模态工况试验的断裂韧度均存在一定的率相关性：随着应变率的提高，当模态角为21.8°时的断裂韧度值分别提高0.9%，26.5%和47.8%；当模态角为41.7°时的断裂韧度值分别提高5.3%，22.1%和32.6%；当模态角为60.3°时的断裂韧度值分别提高6.2%，29.6%和40.8%。混凝土/花岗岩复合试件率敏感性机理可表征为：随着应变率的提高，裂缝尖端微裂缝产生速率加快、数量增多，消耗的能量更多，造成试件强度增加，从而使Ⅰ型、Ⅱ型断裂韧度值增大。

表3 计算结果Tab.3 The calculation results

图8 断裂韧度与应变率的关系Fig.8 Relationship between fracture toughness and strain rate

当以模态比(Ⅰ型和Ⅱ型断裂韧度的纵向数据对比)作为变量，发现每一应变率时的断裂韧度值均具备模态比相关性。以最小模态角21.8°作为基准，随着模态角的增加，荷载值逐渐增加，Ⅰ型断裂韧度逐渐减小，Ⅱ型断裂韧度逐渐增加。以Ⅱ型断裂韧度为例，发现其值在应变率为10-5s-1时分别提高65.5%和89.9%；在应变率为10-4s-1时分别提高72.7%和99.9%；在应变率为10-3s-1时分别提高59.7%和94.5%；在应变率为10-2s-1时分别提高48.5%和80.9%。断裂韧度在每种应变率工况的模态变化程度均非常显著，原因在于模态角越大，界面位置会逐渐靠近试件中心，主要分载点(左侧)远离界面，岩石侧承载比例增强，使复合试件的承载能力增加。同时，随模态角度增加，复合试件承受的剪切荷载分量增加，正应力分量相对减小，从而表现出Ⅰ型和Ⅱ型韧度值的模态敏感性。

2.4 应变能释放率的率相关性及模态比相关性分析

应变能释放率G是对结构断裂分析时除断裂韧度之外的另一重要参量，用以描述裂缝的扩展能力，受复合应力强度因子的影响。利用均质材料求解应变能释放率的方式，假设界面裂缝由初始长度a沿着界面扩展了长度Δa，通过积分变换，得出界面裂缝的应变能释放率的表示式如下

(3)

根据上述定义，每种工况下的应变能释放率计算结果列如表3所示，每种应变率下应变能释放率G和模态角ψ之间的关系如图9所示。通过线性回归可以发现，应变率在10-5～10-3s-1时，应变能释放率随模态角的增大而增加；当应变率为10-2s-1时，数据点的离散性较大，反映出的提高程度不明显。以应变率作为单一变量分析，发现应变率对应变能释放率(以断裂韧度的平均值计算得到的G值分析)的作用效果显著：随着应变率的提高，应变能释放率的值在模态角为21.8°时分别提高1.8%,59.9%和118.4%；在模态角为41.7°时分别提高10.8%,49.1%和75.9%；在模态角为60.3°时分别提高12.7%,68.0%和98.4%。

图9 应变能释放率与模态角的关系Fig.9 Relationship between strain energy release rate and mode angle

3 结 论

通过对混凝土/花岗岩复合试件进行四点剪切动态试验，可以得出以下结论：

(1)复合试件在各试验工况条件下均从界面处破坏。每种模态工况的复合试件在断裂前的初始刚度基本一致，并且同一时刻时的裂缝张开位移均大于裂缝剪切位移。

(2)断裂韧度具有率敏感性和模态比相关性。界面Ⅰ型和Ⅱ型断裂韧度的值均随应变率的提高而逐渐增加，Ⅰ型断裂韧度随着模态角的增大而减小，Ⅱ型断裂韧度随着模态角的增大而增加，且本试验下的界面破坏可由以断裂韧度点(K2C，K1C)构成的椭圆准则来描述。

(3)以模态角作为单一变量，各试验应变率下应变能释放率的值随模态角的增大而增加；以应变率作为单一变量，各模态工况下应变能释放率的值随应变率的提高而增加，并且提高程度十分显著。