内凹-反手性蜂窝结构的面内动态压溃性能研究

魏路路， 余 强， 赵 轩， 朱国华

(长安大学 汽车学院，西安 710064)

拉胀蜂窝材料作为一种负泊松比材料在单轴拉伸(或压缩)作用下呈现横向膨胀(或收缩)的特性[1]。由于其独特的变形特性，拉胀蜂窝材料较传统材料具有更为卓越的剪切刚度、抗冲击性、抗压痕性及能量吸收特性，在航空航天、汽车、座椅等领域具有广泛的应用前景[2-3]。与传统蜂窝结构相比，拉胀蜂窝材料在微观结构和变形模式方面均呈现其独特性，其内凹及旋转变形机制使蜂窝在变形时呈现负泊松比效应[4]。因此，如何构建蜂窝拉胀材料胞元的微结构、优化其变形机制、提高材料抗冲击性及能量吸收性能成为拉胀蜂窝材料力学性能研究的热点。

内凹蜂窝结构及手性蜂窝结构的力学特性已经被大量研究。Lakes[5]首次利用聚氨酯泡沫得到了负泊松比泡沫材料。Caddock等[6-7]通过聚四氟乙烯微孔结构实现了负泊松比效应。此后，更多的负泊松比材料被设计，例如手性结构、星型结构、双箭头结构和内凹结构等。Hou等[8]分析了内凹蜂窝结构的面内动态破碎行为，并与传统蜂窝结构进行了对比。Li等[9]通过在内凹六边形结构中增加正弦曲线韧带及多阶内凹六边形的方式提高面内抗冲击性能及能量吸收能力。Liu等[10]利用有限元方法研究了内凹六边形结构的动态破碎行为和能量吸收性能，并分析了不均匀内凹六边形结构对动态破碎行为的影响。通过数值模拟的方法，Zhang等[11]研究了微结构对内凹六边形蜂窝面内动态破碎行为的影响，并讨论了胞壁角、冲击速度、长细比对蜂窝结构变形模式、平台应力和能量吸收特性的影响，指出平台应力与冲击速度的平方呈正比。Wang等[12]利用内凹六边形结构与星型结构结合得到内凹-星型拉胀蜂窝结构，对不同冲击模式下蜂窝的变形模式及负泊松比效应进行分析，并利用能量法估算低速及高速冲击载荷下的平台应力。

手性蜂窝结构在面内压缩载荷作用下圆环节点转动，并带动韧带绕圆环节点缠绕，从而实现能量吸收及负泊松比效应[13]。卢子兴等[14]对4-韧带手性、6-韧带手性结构不同冲击速度、韧带长度及厚度下的变形模式及能量吸收性能进行了研究。Alderson等[15-16]研究了3-韧带手性、4-韧带手性、6-韧带手性、反手性结构、内凹手性、内凹反手性的面内弹性，并得到了不同几何参数下的杨氏模量和泊松比。Jiang等[17]通过手性结构与内凹结构相结合，提出一种新型手性蜂窝结构，讨论了不同胞元尺寸和内凹角下蜂窝的拉伸性能。Hu等[18-19]通过实验和仿真的方法研究了内凹-反手性蜂窝(re-entrant anti-trichiral honeycomb，RATH)准静态载荷下的力学性能，并推导了不同变形阶段蜂窝的压溃应力及泊松比的理论公式；指出蜂窝的变形受韧带弯曲和圆环节点转动的影响，压溃应力受整体应变、几何参数和基体材料的影响。目前，受制备工艺和基体材料的限制，对内凹-反手性蜂窝结构的研究主要集中在准静态载荷下的力学性能方面，对于面内动态冲击性能的研究多集中于经典拉胀蜂窝材料，而内凹-反手性蜂窝面内动态冲击压溃性能的研究尚未有相关的文献资料。然而，蜂窝材料作为填充构件用于碰撞防护及抵抗冲击时均承受的是动态冲击载荷。因此，研究内凹-反手性蜂窝的面内动态响应及抗冲击性能显得尤为必要。

本文以内凹-反手性蜂窝为研究对象，采用数值模拟的方法对不同冲击速度下内凹-反手性蜂窝的变形模式、临界冲击速度、平台应变及平台应力进行研究，并讨论中低速冲击时内凹-反手性蜂窝不同变形阶段的能量吸收性能。此外，深入讨论了内凹与手性组合结构蜂窝的面内动态响应，并与三边反手性蜂窝结构进行对比。通过对内凹-反手性蜂窝面内动态压溃性能的研究，揭示内凹与旋转组合变形机制蜂窝的抗冲击特性，从而为探索新型拉胀蜂窝结构奠定基础。

1 模型构建及临界冲击速度

1.1 内凹-反手性蜂窝的几何模型

内凹-反手性拉胀蜂窝是将内凹六边形结构与反手性结构相结合得到的一种拉胀结构材料，其中包含内凹及旋转两种变形机制，图1为内凹-反手性蜂窝结构的示意图及几何参数。该拉胀蜂窝结构利用反手性拉胀结构圆环节点替换内凹六边形顶角(圆虚线标记)得到的一种拉胀蜂窝材料。图中：l为倾斜韧带的长度；h为两个水平相邻圆环节点的距离；r为圆环节点的半径；t为胞壁及圆环节点的壁厚；θ为水平韧带与倾斜韧带之间的夹角。

图1 内凹-反手性蜂窝的结构及几何参数Fig.1 Configuration and geometric parameters of RATH

对于周期性拉胀蜂窝材料，其变形模式及能量吸收特性均与蜂窝结构的相对密度有关。蜂窝结构的相对密度可用蜂窝结构单元实体部分的面积与蜂窝结构单元的横断面积之比表示，因此内凹-反手性拉胀蜂窝结构的相对密度为

(1)

式中：ρ*为拉胀蜂窝结构的表观密度；ρs为拉胀蜂窝结构的基体材料密度。

1.2 有限元模型

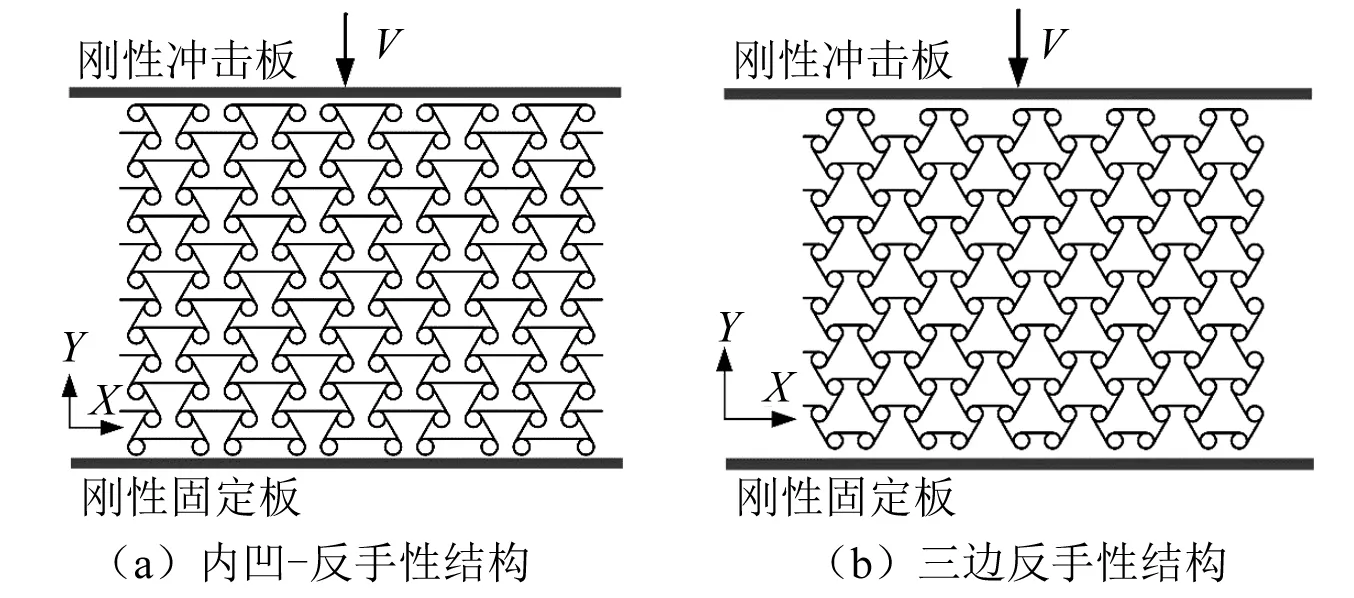
图2 两种拉胀结构的面内冲击有限元模型Fig.2 Finite element models for two honeycombs under in-plane impact

1.3 有限元模型验证

为确保本文有限元模型的准确性，选用Hu等研究的内凹-反手性蜂窝准静态压溃实验的材料属性建立有限元模型，并与Hu等研究的试验结果进行对比。图3为内凹-反手性蜂窝有限元模型的变形过程与试验模型的对比。在相同压缩应变下，有限元模型的变形模式与实验结果基本吻合，均在靠近冲击端呈现出向内收缩的变形模式。内凹-反手性蜂窝的仿真与实验的应力-应变曲线对比如图4所示。在压缩过程中，有限元仿真得到的应力-应变曲线与实验结果具有较高的一致性。从而可以验证，本文建立的有限元模型具有较高的准确性，可以用于后续的研究。

图3 有限元模型与试验模型的变形对比Fig.3 Comparison of deformation processes between FE models and experimental models

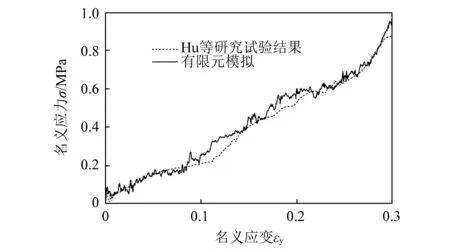
图4 内凹-反手性蜂窝的仿真与实验的应力-应变曲线对比Fig.4 Comparison of stress-strain curves for the RATH between test and simulation

1.4 临界冲击速度

在动态冲击载荷作用下，冲击速度的变化将影响蜂窝的动态变形行为。当冲击速度足够高时，应力幅值超过蜂窝的屈服应力，蜂窝出现局部塑性变形。在临界状态，导致塑性变形的加载速度被称为屈服速度或第一临界速度。Hönig等[20]基于“陷波”理论得到单轴应力载荷下临界速度的解析式，由此可得vcr1

(2)

随着冲击速度的增大，蜂窝的局部变形更为明显。蜂窝受“压实波”的影响由冲击端以逐层连续的方式坍塌，该应力波被称为“稳定波”[21]。与其相对应的冲击速度被称为第二临界冲击速度，即

(3)

2 数值结果与讨论

2.1 变形模式

动态冲击载荷下，蜂窝的变形模式受冲击速度变化的影响，对2 m/s，25 m/s，100 m/s三种不同冲击速度下蜂窝的变形模式进行研究。图5给出了2 m/s冲击时两种蜂窝的变形历程，两种蜂窝的变形过程均呈现出两个变形阶段。第一阶段为韧带旋转内凹并绕圆环节点缠绕及圆环节点的旋转，如图5(a)～图5(c)所示。在初始时刻，与内凹六边形蜂窝变形相似，内凹-反手性蜂窝在x方向整体向内收缩，在冲击端和固定端分别出现“V”形和“倒V”形的局部变形带(见图5(a))。随着压缩应变的增大，内凹-反手性蜂窝的横向收缩更为明显，韧带更为紧密的缠绕在圆环节点上，表现出典型的“><”形颈缩(见图5(b)～图5(c))。相反，三边反手性蜂窝在变形初始阶段仅在冲击端形成“︶ ”形的变形带，且在压缩过程中蜂窝的变形呈四周密实化而芯部中空的变形模式，横向收缩无内凹-反手性蜂窝明显;第二阶段均为圆环节点胞壁的坍塌(见图5(d))，两种蜂窝的韧带均缠绕在圆环节点上，且各圆环节点的胞壁已相互接触，在冲击载荷的作用下圆环节点的胞壁变形并坍塌，蜂窝趋于密实化。

图5 2 m/s冲击速度时三边反手性及内凹-反手性蜂窝的变形模式(t=0.364)Fig.5 Deformation modes of RATH and ATH under impact velocity of 2 m/s(t=0.364)

随着冲击速度增大(25 m/s)，两种蜂窝的冲击端均呈现出明显的局部变形带(见图6(a))，其变形主要为圆环节点胞壁的坍塌，惯性效应逐渐增强。随着压缩应变的增大，靠近蜂窝冲击端中部的胞元变形主要为倾斜韧带的弯曲变形，两侧胞元的变形为韧带旋转内凹并绕圆环节点缠绕及圆环节点的旋转，出现明显的局部“颈缩”现象，蜂窝呈现出明显的“V”形变形带(见图6(a)～图6(b))。然后局部“V”形变形带逐渐向固定端扩展，圆环节点逐渐堆积在一起并趋于密实化(见图6(c))，在冲击载荷的作用下圆环节点逐渐坍塌，直至蜂窝被完全压实。然而，三边反手性蜂窝在中速冲击时靠近冲击端胞元的韧带绕圆环节点缠绕，并逐层周期性向固定端扩展，直至圆环节点堆积在一起被完全压实，变形中无明显横向收缩。在该冲击模式下，两种蜂窝的变形均呈现出与低速冲击模式相似的两个变形阶段。

图6 25 m/s冲击速度时三边反手性及内凹-反手性蜂窝的变形模式(t=0.364)Fig.6 Deformation modes of RATH and ATH under impact velocity of 25 m/s(t=0.364)

高速冲击时(100 m/s)，惯性效应起主导作用。两种蜂窝均呈现出与普通蜂窝相似的变形模式，靠近冲击端的韧带和圆环节点首先被压溃，形成“I”形的变形带，并由冲击端向固定端逐层坍塌，直至蜂窝完全密实化。在该冲击模式下，蜂窝的变形几乎无横向收缩，观察不到“颈缩”现象，如图7所示。

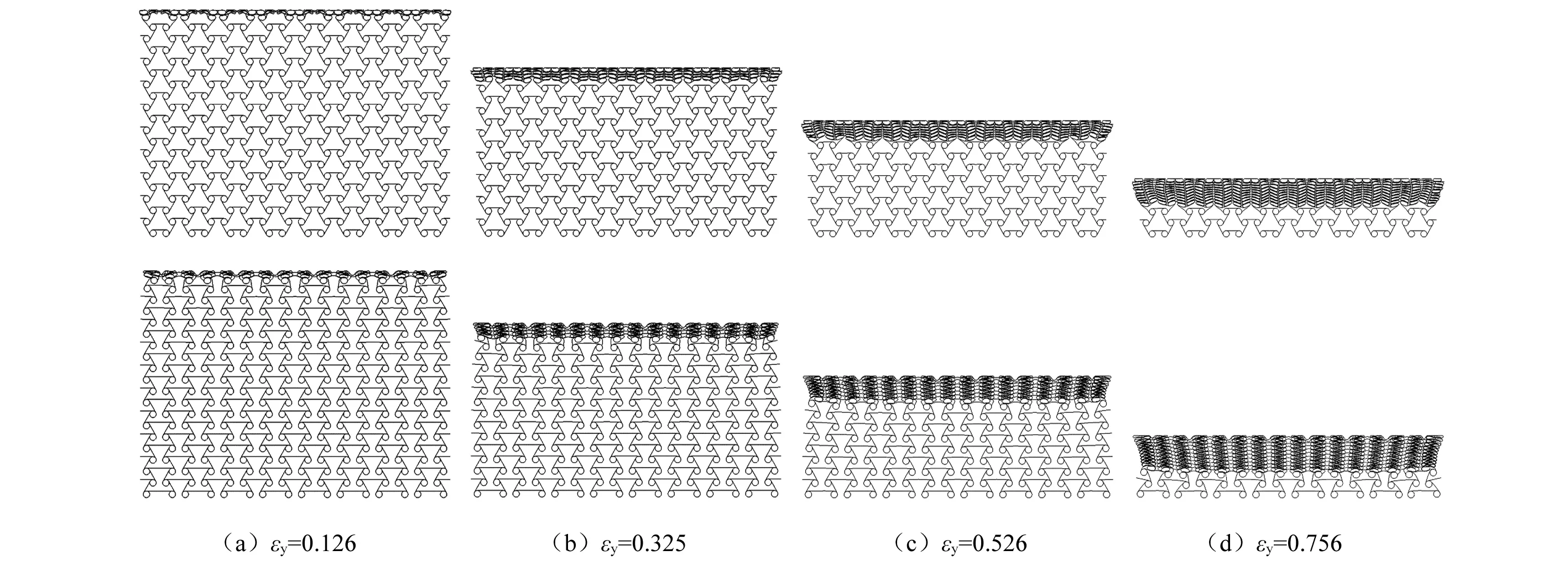
图7 100 m/s冲击速度时三边反手性及内凹-反手性蜂窝的变形模式(t=0.364)Fig.7 Deformation modes of RATH and ATH under impact velocity of 100 m/s(t=0.364)

典型拉胀蜂窝材料在变形过程中仅呈现胞壁内凹收缩的内凹变形机制或圆环节点旋转收缩的旋转变形机制。然而，内凹-反手性蜂窝在中低速冲击时呈现出内凹和旋转混合的变形机制。图8为中低速冲击时内凹-反手性蜂窝的变形机制图。在冲击载荷下，韧带L1和K1分别以不同的转动方向带动胞元左侧内凹收缩(见图8(a))，使蜂窝的变形呈现内凹变形机制。同时，两个韧带不同的转动方向又促使圆环节点O3以顺时针方向转动(见图8(b))，蜂窝又呈现旋转变形机制，并进一步促进蜂窝的横向收缩。同理，胞元的右侧韧带与圆环节点出现与左侧相同的变形机制。因此，内凹-反手性蜂窝变形时，内凹变形机制首先主导蜂窝的横向收缩变形，使其呈现出局部“V”形变形带；同时，韧带的不同转动方向促使圆环节点的旋转，且倾斜韧带绕圆环节点缠绕，使蜂窝整体横向收缩，负泊松比效应更为明显(见图8(c))。随着圆环节点的转动，水平韧带弯曲并缠绕至圆环节点上，蜂窝将进一步横向收缩，圆环节点的等效壁厚增大，蜂窝芯部趋于密实化(见图8(d))。

倾斜韧带绕圆环节点旋转变形时，在韧带的A点、B点、C点和D点产生塑性铰(见图8(b)虚线圆)，吸收冲击载荷产生的能量。随着韧带的旋转及绕圆环节点的缠绕，塑性铰吸收的能量增大，冲击应力呈现出平台期，如图9(a)所示。由于水平韧带绕圆环节点缠绕，在水平韧带两端的E点和F点也产生塑性铰(见图8(c))。此时，蜂窝的能量吸收能力增强，冲击应力及能量吸收效率均呈现逐渐增大的趋势，如图9(a)所示。当韧带完全缠绕至圆环节点上，圆环节点的等效壁厚增大，在冲击载荷的作用下圆环节点胞壁坍塌，冲击应力将迅速增大，直至蜂窝胞壁相互接触，进入密实化阶段，如图9(a)～图9(b)所示。

图8 中低速冲击时内凹-反手性蜂窝的变形机制Fig.8 Deformation mechanism of RATH under low-andmedium-velocity impact

图9 内凹-反手性蜂窝应力-应变及能量吸收效率曲线Fig.9 Stress-strain and energy absorption efficiency curves of RATH

由上述变形过程分析可得，不同冲击速度下内凹-反手性蜂窝呈现出不同的变形模式。而临界冲击速度可从理论上精确的划分蜂窝变形模式的边界，且临界冲击速度受蜂窝的相对密度影响。因此，通过对不同相对密度的内凹-反手性蜂窝在不同冲击速度下的数值模拟，基于线性回归理论可得到临界冲击速度的经验式(4)和式(5)。根据两临界冲击速度将内凹-反手性蜂的变形分为三种模式：vv时为局部变形模式(L-model)，蜂窝呈现“I”形变形带。由此可得，内凹-反手性蜂窝在不同冲击速度和相对密度下的变形模式如图10所示。

图10 内凹-反手性蜂窝的变形模式图Fig.10 Deformation modes of RATH

vcr1=5.2

(4)

(5)

2.2 平台应变及平台应力

与传统蜂窝的变形不同，内凹-反手性蜂窝的变形及应力变化均呈现两个不同的阶段。图9给出了内凹-反手性蜂窝的应力-应变及能量吸收效率曲线。其中应力-应变曲线的两个变化阶段为：韧带旋转内凹并绕圆环节点缠绕过程呈现平台应力阶段，圆环节点胞壁坍塌过程呈现应力迅速增大阶段。因此，内凹-反手性蜂窝的平台应力阶段仅为整个应力变化过程的一部分，其平台应力由式(6)可得

(6)

式中：ε0为初始峰值应力时对应的应变；εp为内凹-反手性蜂窝平台应力阶段结束时刻对应的应变(平台应变)。与密实化应变εd相同，εp是一个速度敏感性变量。因此，基于能量吸收效率的方法确定内凹-反手性蜂窝的这两个应变，密实应变εd可定义为

(7)

式中，E(ε)为蜂窝吸收的能量与名义应力的比值，即

(8)

图9中内凹-反手性蜂窝的能量吸收效率-应变曲线上有多个局部极大值点，取最后一个局部极大值点对应的应变为密实化应变εd，能量吸收效率趋于平稳之前的一个局部极大值点对应的应变为平台应变εp。图11给出了不同壁厚的蜂窝在不同冲击速度下的平台应变。随着冲击速度的增大，平台应变εp逐渐增大，平台应力阶段持续的时间增长。当冲击速度小于第二临界速度(vv)时，平台应变与胞壁厚度t的变化呈反比。

图11 不同冲击速度及壁厚下内凹-反手性蜂窝的平台应变Fig.11 Variations of plateau strains for RATH with different cell wall thicknesses under various impact velocities

图12给出了不同冲击速度下不同胞壁厚度的蜂窝的密实化应变。与平台应变的变化相同，密实化应变与冲击速度的变化呈线性增大关系，与胞壁厚度的变化呈反比。然而，中低速冲击时圆环节点胞壁坍塌与高速冲击时胞元的逐层坍塌过程相似。因此，不同冲击速度时内凹-反手性蜂窝的密实化应变相差不多(2 m/s与100 m/s冲击时仅差0.045)。此外，随着冲击速度的增大，惯性效应逐渐起决定作用，平台应变εp增大并逐渐接近密实化应变εd。当冲击速度为100 m/s时，内凹-反手性蜂窝的平台应变与密实化应变相同。

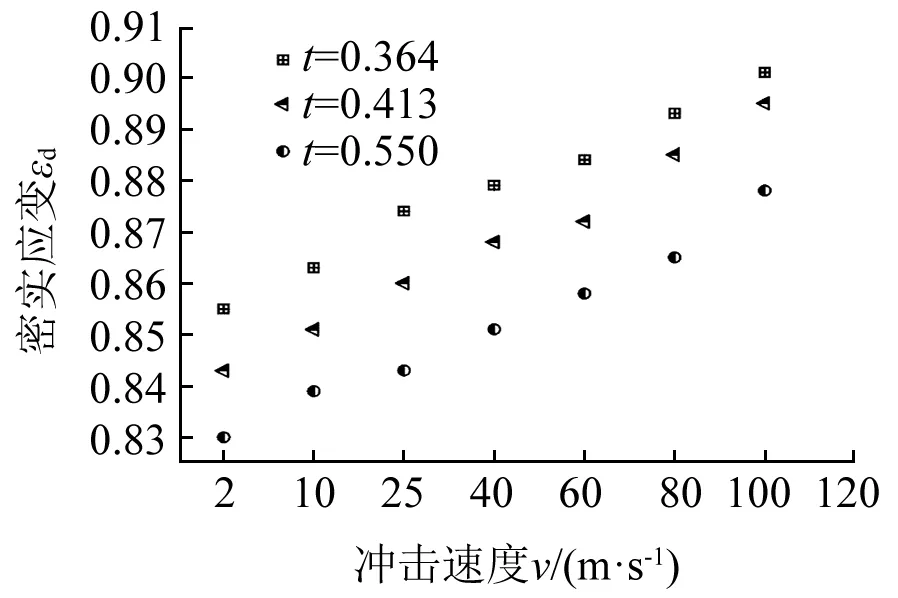
图12 不同冲击速度及壁厚下内凹-反手性蜂窝的密实化应变Fig.12 Variations of densification strains for RATH with different cell wall thicknesses under various impact velocities

Qiu等[22]基于一维冲击波理论对蜂窝的动态冲击平台应力经验公式进行优化，得到了蜂窝材料平台应力的简化公式

(9)

式中：σys为蜂窝基体材料的屈服应力；A和B为经验公式的拟合系数。

通过对不同相对密度的内凹-反手性蜂窝在不同冲击速度下的数值模拟，根据式(6)得到相对应的平台应力。由式(9)，基于最小二乘法拟合的方法得到内凹-反手性蜂窝动态冲击平台应力的经验公式

(10)

图13给出了不同相对密度的内凹-反手性蜂窝的动态冲击平台应力的数值结果与式(10)的对比。由图可得，式(10)能够较好的预测内凹-反手性蜂窝的动态冲击平台应力。此外，平台应力的大小与蜂窝的相对密度和冲击速度相关。随着相对密度和冲击速度的增大，内凹-反手性蜂窝的平台应力明显增大。其中，冲击速度对内凹-反手性蜂窝平台应力的增大作用更为显著。

图13 不同相对密度及冲击速度下内凹-反手性蜂窝的平台应力Fig.13 Variations of plateau stresses for RATH with different cell wall thicknesses under various impact velocities

2.3 能量吸收性能

能量吸收性能是蜂窝力学性能的一个重要指标，因此对内凹-反手性、三边反手性及传统六边形蜂窝的能量吸收性能进行对比分析。由于三种蜂窝结构的几何尺寸存在差异，采用蜂窝的比吸能(specific energy absorption, SEA)进行对比研究。蜂窝结构的SEA被定义为

(11)

式中：U为蜂窝的总吸收能量；σ(ε)为蜂窝的名义应力。

图14给出了内凹-反手性、三边反手性及六边形蜂窝(hexagon honeycomb, HH)在不同冲击速度下的能量吸收性能对比。不同冲击速度下内凹-反手性蜂窝的能量吸收能力均大于三边反手性蜂窝。表1给出了三种蜂窝SEA的详细对比。内凹-反手性蜂窝的SEA比三边反手性蜂窝2 m/s冲击时提高157.35%，比25 m/s冲击时提高63.01%，而高速冲击时两蜂窝的SEA相差不多。此外，由于低速冲击时内凹-反手性蜂窝在内凹变形阶段产生的塑性铰较少，其SEA在变形初始阶段(εy<0.4)小于三边反手性。随着内凹-反手性蜂窝横向收缩，圆环节点旋转挤压水平韧带，导致胞元的所有韧带均出现塑性铰，且蜂窝芯部更为致密化，内凹-反手性蜂窝的SEA逐渐增大，甚至超过25 m/s冲击速度时三边反手性蜂窝的SEA。

表1 不同冲击速度下蜂窝的能量吸收能力Tab.1 Energy absorption capacity of honeycombs under different impact velocities

由于正六边形蜂窝的孔隙率较大，且低速冲击时每个胞元产生的塑性铰是固定的，因此其SEA随压缩应变均匀增大。然而在低速冲击时，随着压缩应变的增大，内凹-反手性蜂窝逐渐横向收缩趋于密实化。胞元的倾斜和水平韧带产生的塑性铰逐渐增多，且韧带缠绕至圆环节点上增大了圆环节点的等效壁厚，内凹-反手性蜂窝能量吸收能力逐渐增强。因此，内凹-反手性蜂窝的能量吸收能力在压缩应变εy<0.6时小于正六边形蜂窝，然后超越并迅速增大，如图14所示。且可以看出，不同冲击载荷下内凹-反手性及三边反手性蜂窝均呈现出比正六边形蜂窝更优异的能量吸收能力。

图14 不同冲击速度下蜂窝的比吸能对比Fig.14 Comparisons of SEA for honeycombs under different impact velocities

在低速及中速冲击过程中可明显的观察到内凹-反手性蜂窝的比吸能呈两个不同的变化阶段，在平台应力阶段蜂窝的比吸能均匀增长，圆环节点坍塌阶段比吸能将迅速增大。此外，内凹-反手性蜂窝比吸能的两个变化阶段也与蜂窝变形时呈现的两个变形阶段相互对应。

图15给出了冲击速度小于第二临界冲击速度时两变形阶段比吸能相对于总吸收能量的百分比。随着冲击速度的增大，内凹-反手性蜂窝的韧带直接屈曲变形明显，平台应力增大且持续的时间增长，第一变形阶段所吸收的能量也逐渐的增大。此外，变形过程中韧带绕圆环节点的缠绕增大了圆环节点的壁厚，因此在中低速冲击时圆环节点胞壁坍塌(第二变形阶段)所吸收的能量占整个能量吸收的绝大部分。然而，随着冲击速度的增大第二变形阶段吸收的能量占比减小，当冲击速度大于第二临界速度后，蜂窝的坍塌过程仅为胞元的逐层坍塌。

图15 不同变形阶段内凹-反手性蜂窝的能量吸收Fig.15 Energy absorption of RATH with different deformation stages under different impact velocities

2.4 动态泊松比

图16 蜂窝的横向位移测量示意图Fig.16 Schematic diagram of lateral displacement measurement of honeycombs

(12)

(13)

图17给出了不同冲击速度下两种蜂窝的动态泊松比。不同冲击速度下，内凹-反手性蜂窝均呈现出负泊松比特性，而三边反手性蜂窝的泊松比均呈现出由负变正的变化过程，且仅在低速冲击时的变形前期呈现出较弱的负泊松比特性。在动态冲击过程中，冲击速度越大惯性效应越明显，内凹-反手性蜂窝的负泊松比特性越不明显。因此，在中速冲击的初始时刻，动态泊松比的绝对值远远小于低速冲击时刻。随着压缩应变的增大，中低速冲击载荷下蜂窝的变形模式趋于相似。故εy>0.5后，两冲击速度下蜂窝的动态泊松比相差不多。此外，高速冲击时内凹-反手性蜂窝也呈现出较为稳定的负泊松比特性，且其动态泊松比维持在一恒定值波动。由此可得，引入内凹变形机制可有效的提高手性蜂窝的负泊松比效应。

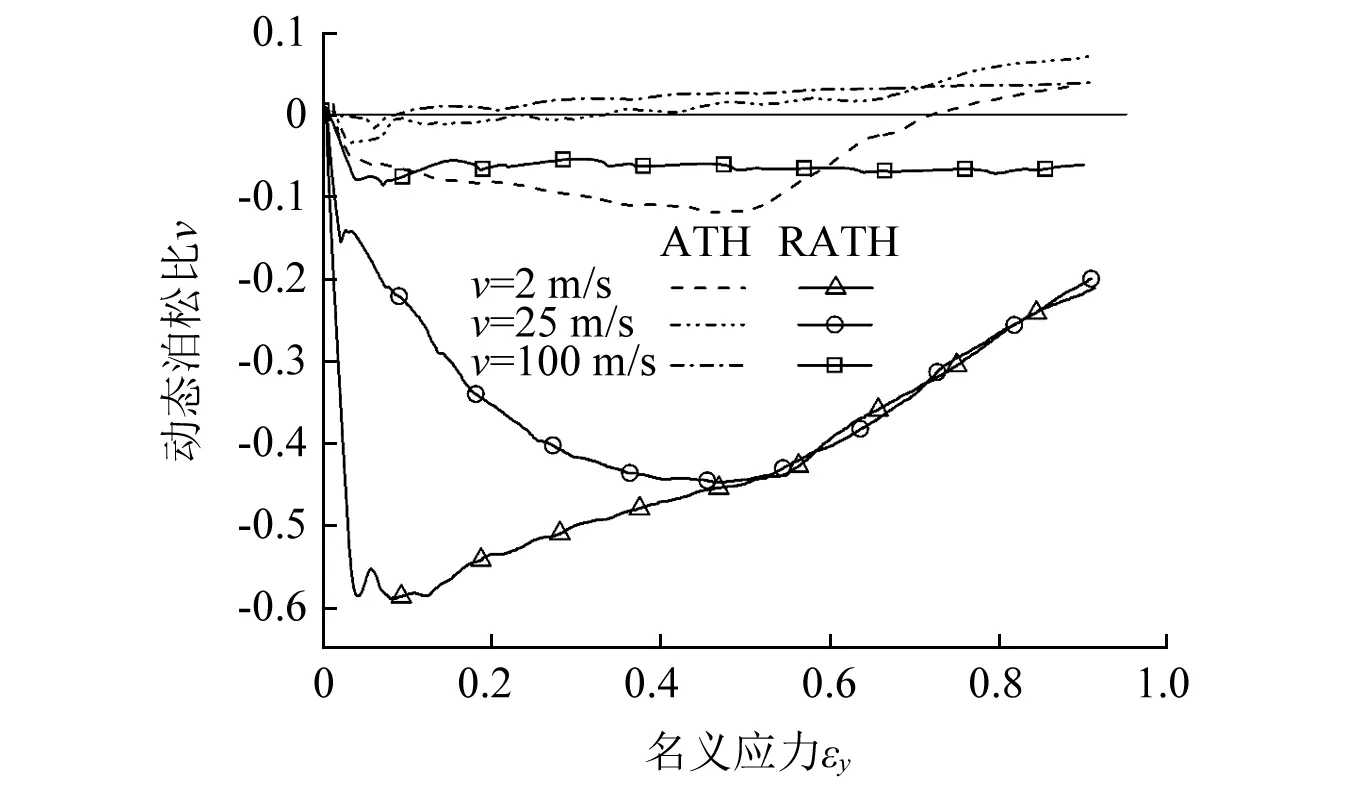
图17 不同冲击模式下蜂窝的动态泊松比对比Fig.17 Comparison of Poisson’s ratio for RATH under different impact models

3 结 论

通过内凹六边形蜂窝与三边反手性蜂窝的结合得到一种内凹-反手性蜂窝结构，利用显示动力有限元软件LS-DYNA对内凹-反手性蜂窝的面内动态压溃性能进行研究，得到如下结论：

(1)具有内凹与旋转组合变形机制的内凹-反手性蜂窝在变形初始阶段同时呈现内凹与旋转两种变形机制，并呈相互促进的关系。随着压缩应变的增大，旋转变形机制起主导作用，水平及倾斜韧带均缠绕至圆环节点上，蜂窝横向收缩，芯部逐渐趋于密实化。

(2)根据能量吸收效率的变化，内凹-反手性蜂窝的应力变化可划分为平台应力阶段和应力增强阶段。其中，平台应力与冲击速度的平方呈正比，且拟合得到的平台应力经验公式与数值模拟结果吻合的较好。

(3)内凹-反手性蜂窝的平台应变及密实化应变均与冲击速度呈正比，与胞壁厚度呈反比。其中，平台应变随冲击速度的增大对胞壁厚度的变化更敏感。

(4)与三边反手性蜂窝及传统蜂窝相比，不同冲击速度下内凹-反手性蜂窝均呈现出优异的能量吸收性能。在中低速冲击模式下，内凹-反手性蜂窝的圆环节点胞壁坍塌所吸收的能量占总吸收能量的比重更高，但随着冲击速度的增大逐渐减小。

(5)引入内凹变形机制可有效提高反手性蜂窝的负泊松比效应。在不同冲击模式下，内凹-反手性蜂窝均呈现出比三边反手性蜂窝更明显的负泊松比效应。