计及运动副间隙的双曲柄六杆压力机机构动力学仿真向量键合图法

王中双， 尹久政

(齐齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006)

平面多体系统在工业生产中应用十分广泛[1-3]，双曲柄六杆压力机机构是典型的该类系统，其低速锻冲和急回特性十分突出，具有较高的推广应用价值。然而，多体系统构件的实际加工及装配均会产生误差，所导致的运动副间隙会引发设备运行中的冲击、振动及噪声问题，给其性能及工作寿命带来不利的影响。因此，计及运动副间隙的平面多体系统动力学研究一直是学术界关注的热点问题[4-7]。现有的运动副间隙碰撞模型多数是以Hertz理论为基础，但在机构实际运动过程中，Hertz定律的假设条件并不能始终得到满足，这会对间隙接触碰撞力描述的准确程度产生影响。为此，文献[8]基于L-N(Lankarani-Nikravesh)碰撞力模型及改进弹性基础模型，提出了一种修正的运动副间隙连续碰撞力混合模型，实际应用中能够更精确地描述运动副间隙。

上述模型的建立方法是以分析力学及弹性力学为基础，对于计及运动副间隙的多种能量形式并存的系统(例如：电机驱动的双曲柄六杆压力机机构系统)，不能用统一的方式实现系统动力学的建模，这在很大程度上制约了该类系统的动力学自动建模与仿真。键合图法[9]从理论上可以有效地解决该类问题，但对于复杂的平面多体系统(例如:计及运动副间隙的双曲柄六杆压力机机构系统)，其标量键合图模型的表达方式过于繁杂，实用价值有限。文献[10]将标量键合图的概念进一步扩展，提出了向量键合图法。不仅可以用统一的方式实现多能域并存系统的建模，还具有表达方式简明、建模过程程式化的特点，对于复杂多体系统动力学计算机建模与仿真问题的研究颇具特色及潜力。

文献[11]基于向量键合图方法，推导出便于计算机建模的系统驱动力矩及运动副约束反力方程，建立了三角形肘杆压力机机构的向量键合图模型，实现了其动力学自动建模与动态静力计算。文献[12]阐述了以广义位移、广义速度向量为关键向量的平面连杆机构向量键合图模型的建立方法，应用相应的算法，在计算机上自动建立了RRR-RRP型平面六连杆压力机机构驱动力矩方程，揭示了脉冲载荷作用下的机构驱动力矩变化规律。文献[13]基于向量键合图的基本概念，推导出便于计算机自动建立的系统状态方程及运动副约束反力方程的统一公式，实现了计及驱动电机在内的3-RRR型平面并联机器人机构系统动力学计算机建模及仿真，其方法特别适用于多种能量形式并存系统的动力学统一化建模及仿真问题。

上述以向量键合图法为基础的研究工作，均未有涉及到计及运动副间隙的机构动力学问题。文献[14]基于二状态非连续接触运动副间隙模型，建立了考虑运动副间隙的平面四连杆机构向量键合图，对其动态特性进行了分析。由于所建立的机构向量键合图模型存在微分因果关系，使其建立机构动力学方程的过程局限于手工推导。文献[15]以MLSD(massless-link/spring-damper)运动副间隙模型为基础，建立了含转动副间隙的RRR-RRP六连杆压力机机构的向量键合图模型，实现了其计算机自动建模及动力学仿真。但是，其在精确程度及实用性方面具有局限性。

为此，本文基于白争锋的研究所提出的修正非线性连续接触碰撞力混合模型，推导出间隙运动副的相对碰撞速度向量方程，建立了更加精确描述运动副间隙的向量键合图模型，具有通用性强、模块化的特点，便于嵌入到系统的向量键合图模型中。在此基础上，建立了计及驱动电机、运动副间隙的双曲柄六杆压力机机构向量键合图模型。应用王中双等所述算法，实现了机构的计算机建模及动力学仿真。通过对仿真结果的分析讨论，揭示了运动副间隙对双曲柄六杆压力机机构刀具的加速度及运动副约束反力的影响，验证了所述方法的可靠性及有效性。通过与无质量弹簧阻尼运动副间隙模型的计算对比，进一步表明本文方法可以提高系统动力学仿真的精度及实用性。

1 修正非线性连续接触碰撞力混合间隙向量键合图模型

图1为修正非线性连续接触碰撞力混合间隙模型简图，构件Fi为轴套；构件Fj为轴；OFi，OFj分别为轴套和轴的轴心点；RFi，RFj分别为轴套和轴的半径；rFOi，rFOj分别为轴套、轴的轴心点在全局坐标系OXY中的位置向量；δFi，δFj分别为轴套、轴的碰撞点在全局坐标系OXY中的位置向量；e为轴与轴套的偏心向量，其表达式为

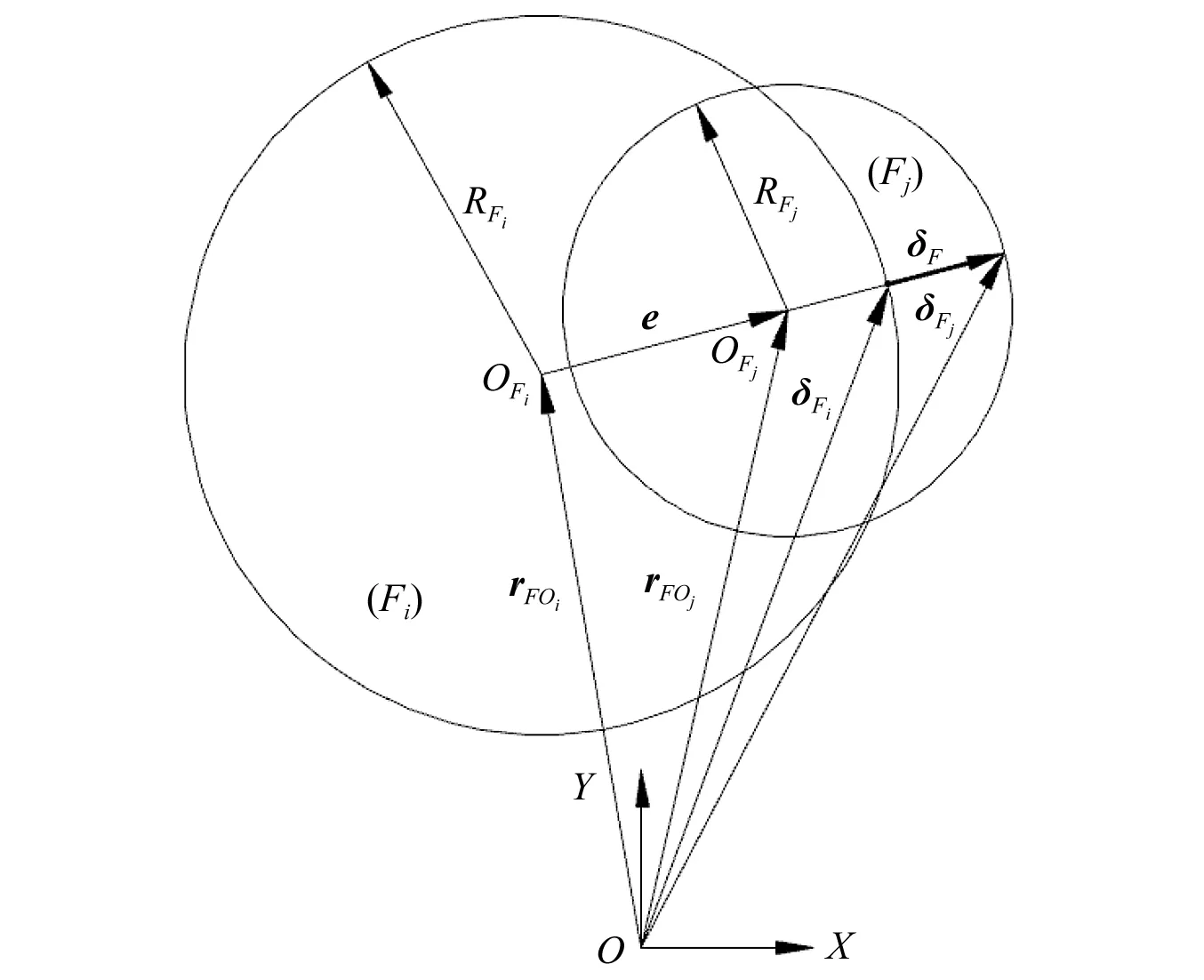
图1 修正非线性连续接触碰撞力混合模型简图Fig.1 An improved hybrid nonlinear continuous contact and collision model

e=rFOj-rFOi

(1)

设δF为轴与轴套相互碰撞的压入深度向量，相应的压入深度δF为

δF=e-c

(2)

式中：c=RFi-RFj，为轴与轴套的半径差；e为轴与轴套的偏心量。

在白争锋的研究基础上，间隙运动副的连续接触碰撞力可以进一步归纳成如式(3)向量形式

(3)

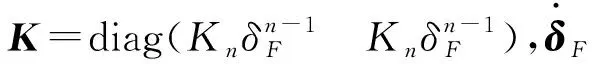
(4)

(5)

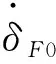
由图1可得向量δF，δFi，δFj间的关系式为

δF=Sn(δF)(δFj-δFi)

(6)

对式(6)两边求导得

(7)

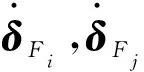
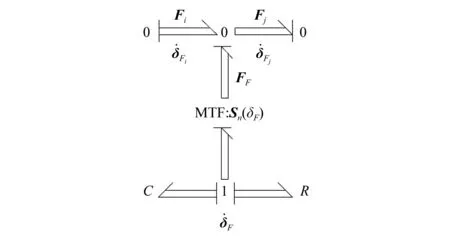
图2 间隙转动副向量键合图模型Fig.2 A vector bond graph model with joint clearance

Behzadipour等和王中双等的研究详细阐述了平面多体系统向量键合图模型的建立方法，将图2所示间隙转动副向量键合图模型嵌入到系统向量键合图模型的相应处，便可以建立计及运动副间隙的平面多体系统向量键合图模型，这为该类系统的计算机建模与仿真奠定了重要基础，下面通过仿真实例对此具体予以说明。

2 计及运动副间隙的双曲柄六杆压力机机构向量键合图模型

由王中双和等的研究可建立该系统永磁式直流驱动电动机的键合图模型，如图4(a)所示。由图3可以看出，该机构是由通用曲柄滑块压力机的曲柄和传动轴之间串联一个双曲柄机构所构成，曲柄AB、连杆BC、曲柄CDE、机架及连杆EF彼此间用转动副连接，滑块(刀具)与机架通过移动副连接。由于机构运行时滑块(刀具)冲切工件会发生碰撞与冲击， 转动副F受实际冲切力的影响最直接，极易产生磨损，故这里仅计及转动副F的间隙。应用Behzadipour等研究所述方法，可以分别建立图3所示机构各构件的向量键合图模型，将其按照机构的上述运动约束关系键接起来，可以建立计及运动副间隙的双曲柄六杆压力机机构向量键合图模型，将其与图4(a)驱动电机的键合图模型进一步键接，可以建立图3所示系统完整的向量键合图模型，如图4所示。其中，间隙转动副F的向量键合图模型如图4(b)所示。

图3 电机驱动含运动副间隙的双曲柄六杆压力机机构Fig.3 Double crank six-bar press mechanism with joint clearance driven by motor

通过上述方法所建立的机构向量键合图模型，同时具有积分因果关系及微分因果关系，直接应用现有的方法进行机构的计算机建模及动力学仿真，代数上的处理非常困难。为此，将该机构各运动副约束反力向量Se5(转动副B)、Se8(转动副C)、Se10(转动副D)、Se12(转动副E)作为未知势源向量，添加在图4相应的0-结处，可以完全消除微分因果关系。如此建立的如图4所示的机构向量键合图，所有贮能元件皆具有积分因果关系，可以直接应用王中双等所述方法实现机构的计算机建模与动力学仿真。

3 计及运动副间隙的双曲柄六杆压力机机构动力学仿真

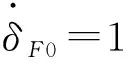
由王中双等所述方法知，与图4所示系统向量键合图相对应的系统独立贮能场独立运动的能量变量向量为

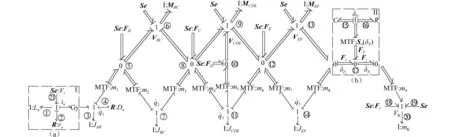
图4 系统向量键合图模型Fig.4 Vector bond graph model of system

(8)

式中，pi(i=1,3,7,11,14)为图2中相应惯性元件的广义动量。

系统独立贮能场非独立运动的能量变量向量

(9)

式中，pix，piy(i=6,9,13)为图4中相应惯性元件的广义动量向量在X轴及Y轴方向的投影；p20为图4中相应惯性元件的广义动量；VBCx，VBCy，VCDEx，VCDEy，VEFx，VEFy分别为相应构件质心速度向量在X轴及Y轴方向的投影；q15x，q15y为图4相应容性元件的广义位移δF在X轴及Y轴方向的投影。

相应的共能量变量向量

[VBCxVBCyVCDExVCDEyVEFxVEFyFFxFFyVK]T

(10)

式中：fi(i=1,3,7,11,14,20)为图4相应惯性元件的流变量；e15x，e15y为图4相应容性元件的势变量向量在X轴及Y轴方向的投影；fix，fiy(i=6,9,13)为图4相应惯性元件的流变量向量在X轴及Y轴方向的投影。

耗散场输入、输出向量分别为

(11)

(12)

式中：ei，fi(i=2,4)分别为图4相应阻性元件的势变量和流变量；e16x，e16y，f16x，f16y分别为图4相应阻性元件的势向量和流向量在X轴及Y轴方向的投影。

系统已知势源向量

U1=[Se21Se6xSe6ySe9xSe9ySe13xSe13ySe18Se19]T=

[Vt0-mBCg0-mCDEg0-mEFgFr-mKg]T

(13)

式中，Seix，Seiy(i=6,9,13)分别为图4相应势源向量在X轴及Y轴方向的投影；Se1，Se18，Se19分别为图4相应的势源。

系统未知势源向量

U2=[Se5xSe5ySe8xSe8ySe10xSe10ySe12xSe12y]T=
[FBxFByFCxFCyFDxFDyFExFEy]T

(14)

式中：Seix，Seiy(i=5,8, 10,12)分别为图4相应势源向量在X轴及Y轴方向的投影；FBx，FBy，FCx，FCy，FDx，FDy，FEx，FEy分别为运动副B、C、D、E约束反力向量在X轴及Y轴方向的投影。

应用王中双等所述方法，由图4可以建立向量Xi1与向量Zi1之间的关系矩阵Fi1、向量Xi2与向量Zi2之间的关系矩阵Fi2、向量Dout与向量Din之间的关系矩阵R。同时，可以建立与图4所示系统向量键合图模型相对应的结型结构矩阵。

将系统状态变量向量Xi1，Xi2的初值、系统的结构参数、已知势源向量U1、矩阵Fi1，Fi2，R及结型结构矩阵代入以王中双等所述算法为基础所编制的MATLAB软件中去，可以用程式化的方式自动建立形式为一阶非线性微分方程组的系统状态方程并求解，部分仿真结果曲线如图5～图7所示。值得说明的是本文所采用的求解器Ode45，其基础算法是变步长Runge-Kutta-Felhberg方法，适用于对精度要求较高的问题，是实际工程中应用较多的有效算法。

对图3所示机构各构件进行受力分析，应用牛顿-欧拉法可以分别建立各运动构件质心加速度与所受外力的关系方程(既牛顿方程)及各构件角加速度与其所受力矩的关系方程(既欧拉方程)，将所得到的二阶微分方程组形式的牛顿-欧拉动力学方程进一步降阶整理并与驱动电机的动力学方程联立，可以得到以Xi1，Xi2为状态变量向量的一阶非线性常微分方程组，这在形式上与用本文方法所得到的系统动力学方程是完全一致的。在MATLAB环境下，选用与本文上述方法同样的求解器、设定同样的参数求解，部分计算结果如表1、表2所示，与本文方法所得结果是完全一致的。将表1、表2所列数据用涂黑的圆点表示在图5～图7中，这些圆点均在对应的仿真曲线上，更加直观地表明了这一点。但是，这一验证过程手工处理量较大，相当繁琐。相比而言，本文所述方法可以用统一的方式使该机电系统的动力学建模、仿真及分析过程以程式化的方式由计算机来完成，提高了该类工作的效率及可靠性。

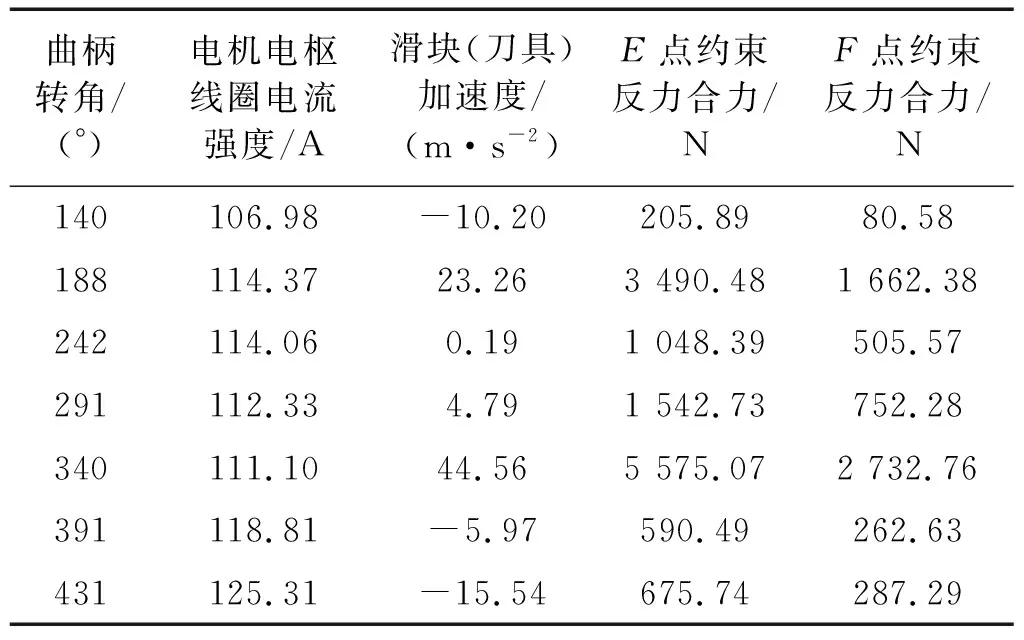
表1 无间隙机构牛顿-欧拉动力学方法部分计算结果Tab.1 Some results without clearance calculated by Newton-Euler dynamic method

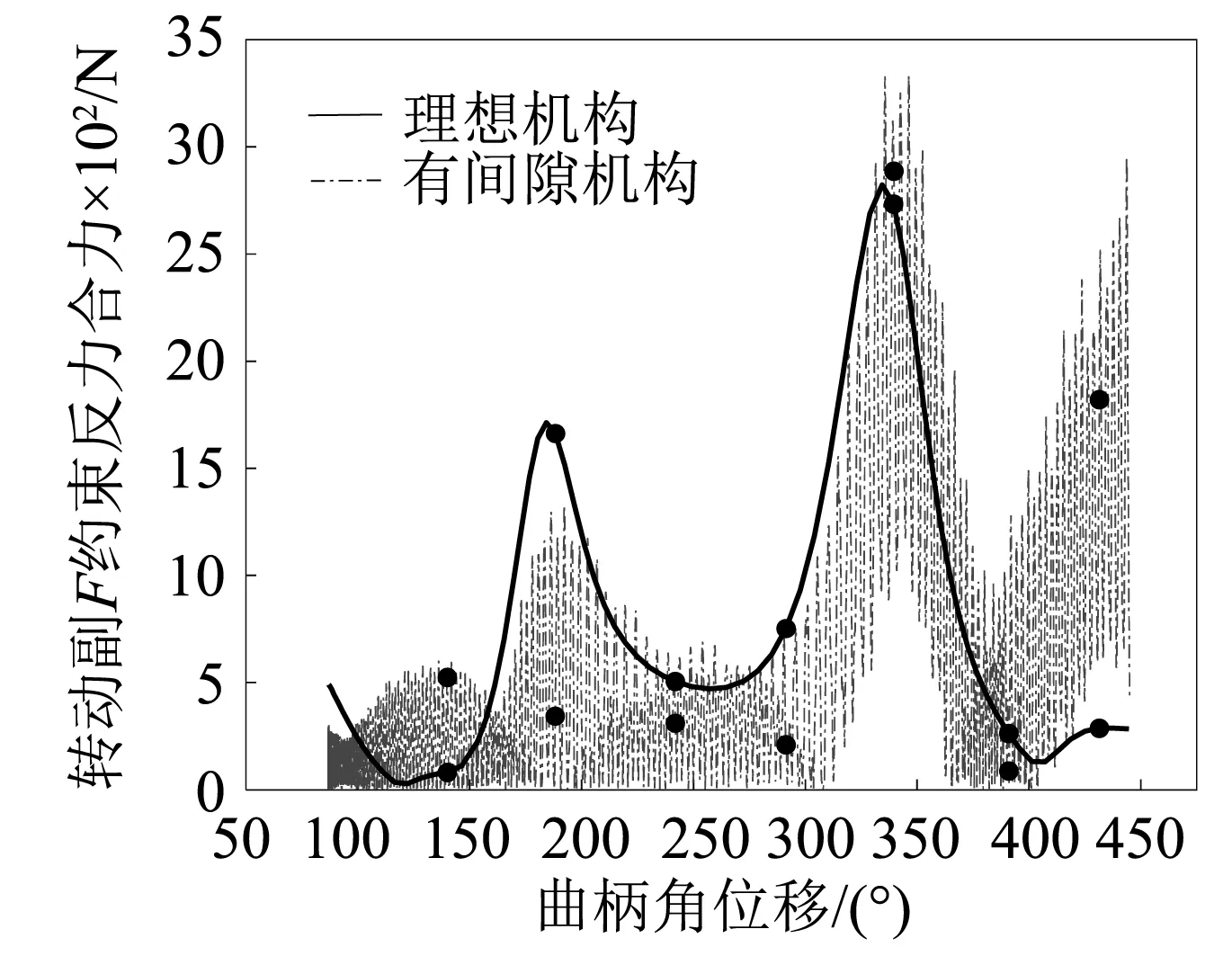
图5 转动副F约束反力合力Fig.5 Resultant constraint force of joint F

图6 滑块(刀具)加速度曲线Fig.6 Acceleration of slider (cutter)

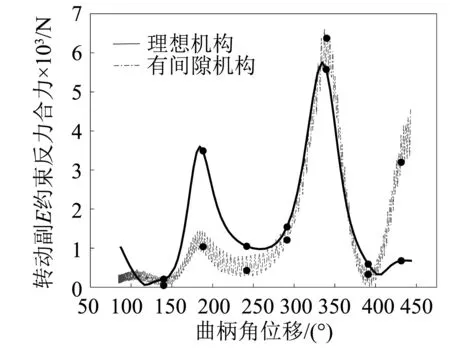
图7 转动副E约束反力合力Fig.7 Resultant constraint force of joint E

表2 有间隙机构牛顿-欧拉动力学方法部分计算结果Tab.2 Some results with clearance calculated by Newton-Euler dynamic method

图5～图7中，曲柄角位移的初值为87°(对应刀具上极限位置)。曲柄由该位置逆时针转360°，机构完成一个运动周期。在机构一个工作循环中，对应无间隙机构的动力学仿真曲线均比较光滑。间隙使运动副轴与轴套间产生脉冲式的间隙碰撞力，导致间隙转动副F的约束反力曲线、刀具加速度曲线及无间隙转动副E的约束反力曲线均呈高频振荡状态，在初始点附近表现得尤为明显。另外，转动副F的间隙使其本身的约束反力、(刀具)加速度及转动副E约束反力的最大峰值均显著增大。相比无间隙机构，有间隙机构相应仿真曲线的总体变化趋势相近。具体分析如下：

由图5知，曲柄角位移q1=334°时，无间隙机构转动副F的约束反力最大峰值为2 821.41 N，角位移q1=336°时，有间隙机构转动副F的约束反力最大峰值为3 329.14 N，其最大峰值增加了507.73 N，两者达到最大峰值曲柄角位移相差2°。

由图6知，当曲柄角位移q1=334°时，无间隙机构刀具加速度的最大峰值为47.54 m·s-2，当角位移q1=336°，含间隙机构刀具加速度的最大峰值为55.66 m·s-2，其最大峰值增加了8.12 m·s-2，两者达到最大峰值曲柄角位移相差2°。

由图7知，当曲柄角位移q1=334°时，无间隙机构转动副E约束反力的最大峰值为5 757.34 N，角位移q1=336°时，有间隙机构转动副E约束反力的最大峰值为6 622.33 N，其最大峰值增加了864.99 N，两者达到最大峰值曲柄角位移相差2°。

由此可见，相比无间隙机构，含间隙机构刀具的加速度及运动副约束反力达到最大峰值时曲柄角位移相差均较小。间隙转动副F本身的约束反力、刀具的加速度及转动副E的约束反力对间隙均十分敏感，最大峰值分别增加了18%，17%，15%。其中，间隙转动副F约束反力最大峰值的增长率尤为突出。这会导致压力机机构的实际运行产生较大的冲击、振动及噪声，加剧运动副的磨损，给机构运动的稳定性、零部件的强度及工作寿命均带来不利的影响。

针对本文的机电系统，应用王中双等所述方法，将基于MLSD运动副间隙模型的向量键合图嵌入到本文机电系统的向量键合图模型中，可以建立计及MLSD间隙模型的系统向量键合图模型。在此基础上，采用王中双等研究中MLSD模型的物理参数值，应用与本文同样的建模方法(详见王中双等的研究)实现系统的动力学建模与仿真，其仿真结果曲线如图8～图10所示。

通过与图5～图7对比分析可知，两种方法所得到的间隙转动副F约束反力曲线、刀具加速度曲线及无间隙转动副E约束反力曲线总体变化趋势相近。在曲柄转动的初始阶段，均呈现高频波动状态。但是，随着曲柄角位移的增大，图8～图10所示仿真曲线的波动频率均有所下降，明显低于图5～图7相对应的仿真曲线。图8所示间隙转动副F约束反力曲线的最大值为3 630.61 N，比图5相应曲线的最大值增加了301.47 N；图9所示刀具加速度曲线的最大值为71.23 N，比图6相应曲线的最大值增加了15.58 N；图10所示转动副E约束反力曲线的最大值为7 053.29 N，比图7相应曲线的最大值增加了430.96 N。由此可见，基于MLSD运动副间隙模型所得到的间隙转动副F约束反力、刀具加速度及转动副E约束反力的最大值均有所增加。进一步对比分析可知，图8～图10与图5～图7相对应的仿真曲线取得最大值的时间也皆不相同。

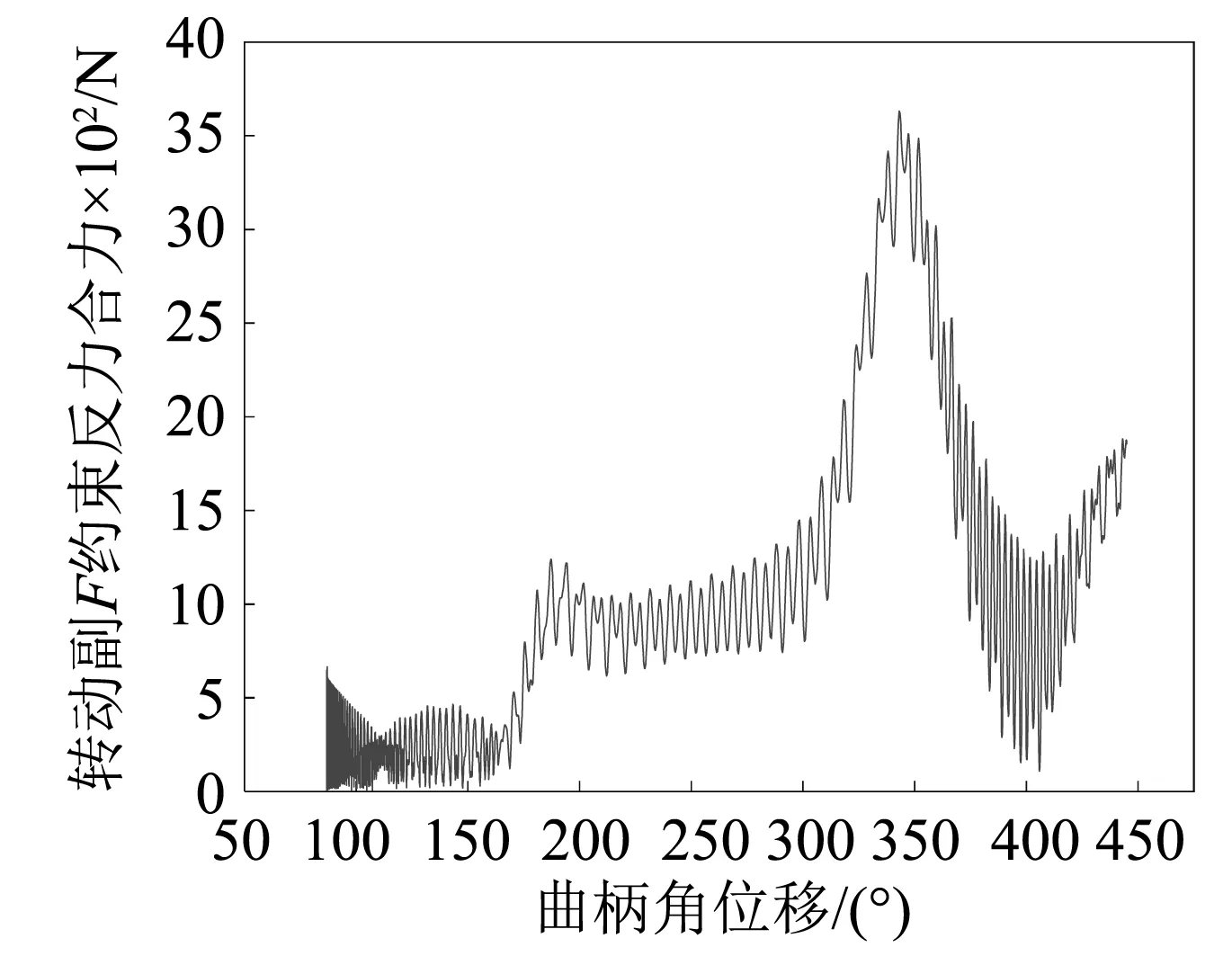
图8 MLSD模型转动副F约束反力合力Fig.8 Resultant constraint force of joint F based on MLSD model

图9 MLSD模型机构滑块(刀具)加速度曲线Fig.9 Acceleration of slider (cutter) based on MLSD model

图10 MLSD模型转动副E约束反力合力Fig.10 Resultant constraint force of joint E based on MLSD model

导致上述两种方法仿真结果出现偏差的主要原因在于机构运行时，其间隙运动副轴与轴套间的碰撞是复杂的非线性过程，MLSD模型是用线性弹簧阻尼描述运动副间隙的弹性及阻性效应，不能真实反映运动副轴与轴套间碰撞过程中的非线性特性。另外，实际应用中准确地给出弹簧阻尼器的弹性系数及阻尼系数比较困难，本文所采用的MLSD模型的具体参数是通过直接引用白争锋和王中双等的研究来获得，这也是导致其仿真结果产生误差的重要原因。相比较而言，本文所建立的模型是用非线性弹簧阻尼描述运动副间隙的弹性及阻性效应，不但能够描述碰撞过程中的能量转换特性，还包含碰撞体本身的材料属性、局部变形及碰撞速度等信息，比较真实客观地反映了间隙运动副的碰撞过程，有效地解决了实际应用中碰撞刚度系数及阻尼系数取值较困难的问题，且不受间隙尺寸和恢复系数的限制。由此可见，应用本文所建立的修正非线性连续接触碰撞力混合间隙向量键合图模型，可以进一步地提高计及运动副间隙的机电系统计算机建模及动力学仿真的精度及实用性。

4 结 论

(1)本文基于修正非线性连续接触碰撞力混合间隙模型，推导出间隙运动副相对碰撞速度向量方程。在此基础上所建立的间隙转动副向量键合图模型，可以用简明的图形方式更精细地描述运动副间隙，具有通用性强、模块化的特点，便于嵌入到平面多体系统向量键合图模型中，为更精确地实现计及运动副间隙的多能域系统计算机建模、动力学仿真及分析奠定了重要基础。

(2)建立了计及驱动电机、运动副间隙的双曲柄六杆压力机机构向量键合图，实现了其计算机统一建模及动力学仿真。验证对比分析表明：本文所述方法是可靠的，进一步提高了系统动力学仿真的精度及实用性，其程式化的建模方式提高了计及运动副间隙的机电系统动力学建模、仿真及分析工作的效率。

(3)通过对具体实例的仿真结果分析，揭示了运动副间隙对电机驱动的双曲柄六杆压力机机构刀具的加速度、运动副约束反力的影响，对于机构的设计、控制及可靠性问题的研究具有一定的价值。

(4)本文工作为同类问题的研究提供了特色鲜明的新途径，进一步拓展了向量键合图理论及应用的研究领域。