基于检测指数判决的子空间方位估计方法
杨 丽, 沈 统, 秦 洁
(沈阳理工大学 装备工程学院,沈阳 110159)
空间目标方位估计一直是雷达、声纳、通讯领域中重要的研究课题[1-4],为了降低空间目标方位估计方法对原始信号最低信噪比需求,人们常采用布阵与信号合成方式提高输出信号信噪比,等价于降低了空间目标方位估计方法对原始信号最低信噪比需求[5-8]。为了提高方位估计分辨率,在信号处理方面,提出采用子空间分解方式实现高分辨方位估计[9-10](本文称之为子空间方法),并在频域和波束域对该方法进行了工程化应用[11-14]。
由于频域和波束域子空间方法在对一帧数据对应协方差估计中,①将一帧时域数据通过傅里叶变换(Fourier transform,FT)转换为不同频点频域数据,实现频域压缩采样;②再对每一频点利用频域单个数据求取该频点协方差矩阵;③通过多帧频域数据累积实现协方差矩阵估计[15-16]。该过程在空间数据非平稳时,难以通过频域多帧数据累积实现协方差矩阵估计,影响子空间分解效果,对实际应用带来了限制[17-18]。如何降低子空间高分辨方位估计方法对空间数据平稳性的要求,提高子空间高分辨方位估计方法在实际应用中的稳健性,是本文需要解决的问题。
本文通过分析影响子空间高分辨方位估计方法稳健性差的因素,提出了一种基于检测指数判决的子空间方位估计方法。该方法完全基于时域处理,在短时内可以获得足够多的时间采样点数,通过一帧数据内时域多个采样点累积降低空间非稳定数据对子空间分解产生的影响;同时依据空间目标在各子空间强度谱检测指数差异,对各子空间合成空间强度谱进行检验统计量判决处理,进一步降低了背景噪声对最终合成空间强度谱影响。同时通过数值仿真及实测数据处理进一步验证了本文方法的有效性。
1 子空间方法
1.1 基本原理
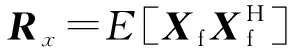
(1)
式中,W(θ)=[ej2πfτ1,ej2πfτ2,…,ej2πfτN]为导向权向量。

(2)
式中,K为一次处理数据分帧数,一般取大于阵列所含传感器数的2倍,以使目标方位估计时的增益损失降低到3 dB以下。
1.2 空间数据影响分析
在频点fi上, 第k帧数据的协方差矩阵可表示为
(3)

由文献[19]可知,一次处理数据帧数K对子空间方法的影响可近似表示为
(4)
式中,σP(θ)为子空间方法所得目标方位估计方差。

(5)
由式(4)和式(5)可知,对空间运动目标实现检测和方位估计时,由于子空间方法一次处理数据分帧数有限,将影响目标检测和方位估计性能。
2 本文方法
2.1 基本原理
由FT分析可知,对于一帧多个时域采样点数据经过FT后,在频域同一频点只包含单个频域数据,再利用单个频域数据求取不同频点协方差矩阵时,容易出现非满秩现象。对此,本文采用时域直接处理方法,通过对一帧多个时域采样点数据的累积,提升协方差矩阵稳定性。
为了能够在时域实现对协方差矩阵的稳定估计,本文根据相位与时延之间的关系,首先在时域构建经时延后的协方差矩阵,求取经时延后的子空间;然后利用延时补偿后信号子空间各通道数据一致性和噪声子空间各通道数据随机性,求取各子空间对应空间强度谱;最后利用空间目标在各子空间强度谱检测指数差异对各子空间合成空间强度谱进行判决处理,合成最终空间强度谱,实现空间目标方位估计。
将接收阵拾取数据按向量形式,可表示为
X=S+V
(6)
式中:S=[s1(t),s2(t),…,sN(t)]T为接收阵各传感器拾取数据中目标信号向量;V=[v1(t),v2(t),…,vN(t)]T为接收阵各传感器拾取数据中噪声向量。

然后,在搜索角度θ上,对各传感器时域复解析数据Y按τn=(rcos(θ-(n-1)α))/c(圆阵)或τn=((n-1)dcosθ)/c(线阵)进行时延补偿,c为声速,r为接收阵半径,d为接收阵相邻阵间距,α=2π/N,1≤n≤N,得经时延补偿后数据。

(7)
式中,φτ=[φτ1,φτ2,…,φτN]T。

(8)

最后,利用延时补偿后信号子空间各通道数据一致性和噪声子空间各通道数据随机性,在无目标先验信息情况下,按式(9)获得本文方法输出空间强度谱
(9)
式中:I1×N=[1,1,…,1]1×N为1×N单位矩阵;αn为合成空间强度谱过程中第n个子空间对应的判决处理因子。
2.2 实现过程
本文算法实现过程可分为以下几个步骤:
步骤1根据空间数据短时平稳特性,对拾取数据进行分帧(将传感器采集I个采样点数据为一个处理单元,即为一帧,相邻两帧之间按L=0.5I长度进行重叠处理)和复解析小波变换处理,得到第k帧复解析数据Y,k=1,2,…,K。
步骤2按式(7)所示,在搜索角度0≤θ≤Θ(Θ为预设搜索角度数)上,对第k帧复解析数据中各传感器数据进行时延补偿。

步骤4按式(10)得到第k帧数据对应的各子空间空间强度谱Pn(k,θ),1≤n≤N。
(10)
步骤5更新搜索角度θ,θ=θ+1,重复执行步骤2~步骤4,直到θ=Θ,得到各子空间在0≤θ≤Θ上的空间强度谱Pn(k,θ)。
步骤6更新处理帧数据,k=k+1,重复执行步骤2~步骤5,直到k=K,使各子空间均得到K个空间强度谱Pn(k,θ),k=1,2,…,K; 0≤θ≤Θ。

(11)

(12)
步骤9求取各子空间空间强度谱对应检测指数系数DT(n),1≤n≤N,并将其作为各子空间判决统计量
(13)
步骤10求取各子空间输出空间强度谱对应判决因子αn,n=1,2,…,N
(14)
式中,T由检测指数系数和检测概率通过纽曼-皮尔逊准则计算所得,一般取T=6[21]。
步骤11在无先验信息情况下,并利用各子空间对应判决因子实现对各子空间强度谱判决处理,得到下最终合成空间强度谱
(15)
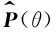
2.3 性能分析

(16)
同样,由于空间噪声子空间不包含空间目标信号,其输出空间强度谱对应最大值Pθ,max、均值Pθ,mean、均方差σθ可表示为
(17)
由式(16)和式(17)可知,目标子空间对应检测指数系数DT(N)和噪声子空间对应检测指数系数DT(n)|n≠N可表示为
(18)
由式(18)可知,在空间噪声稳定情况下,对于空间辐射一定能量的目标信号,目标子空间对应检测指数系数DT(N)将远大于噪声子空间对应检测指数系数DT(n)|n≠N,即DT(N)≫DT(n)|n≠N此时,通过式(14)和式(15)处理,在无先验信息情况下,可有效降低背景噪声对最终合成空间强度谱的影响。
3 数据处理分析
3.1 数值仿真分析
为了进一步对比本文方法和子空间方法在空间目标方位估计方面的性能,接下来进行如下数值仿真。
仿真条件:接收阵为传感器间距2 m的40元均匀分布线列阵,接收阵拾取数据所用采样率为8 kHz,目标信号为两个等强度的信号源(带宽为250~500 Hz),目标方位初始值为30°,60°。其中,方位初始值为60°处的目标在0~100 s内以的方位变化率相对接收阵变化,噪声为空间加性白噪声,目标信号与背景噪声谱级比为-18 dB。具体处理过程如下:①对一次处理长度为16 k个采样数据采用128阶FIR带通滤波器进行250~500 Hz频段滤波处理;②对一次处理数据分125帧处理(单帧数据长度为256,帧与帧之间重叠128个采样数据),对每帧数据做FT分析;③对各频点作协方差矩阵估计、特征分分解、空间强度谱合成。处理中目标先验信息未知,图1和图2分别为子空间方法和本文方法处理所得时间历程图。图3为起始时刻两种方法输出空间强度谱结果。图4为本文方法在无目标先验信息情况时,通过提取检测指数处理所得各子空间强度谱判决因子αn。

图1 子空间方法输出方位历程图Fig.1 Output bearing course diagram of subspace method
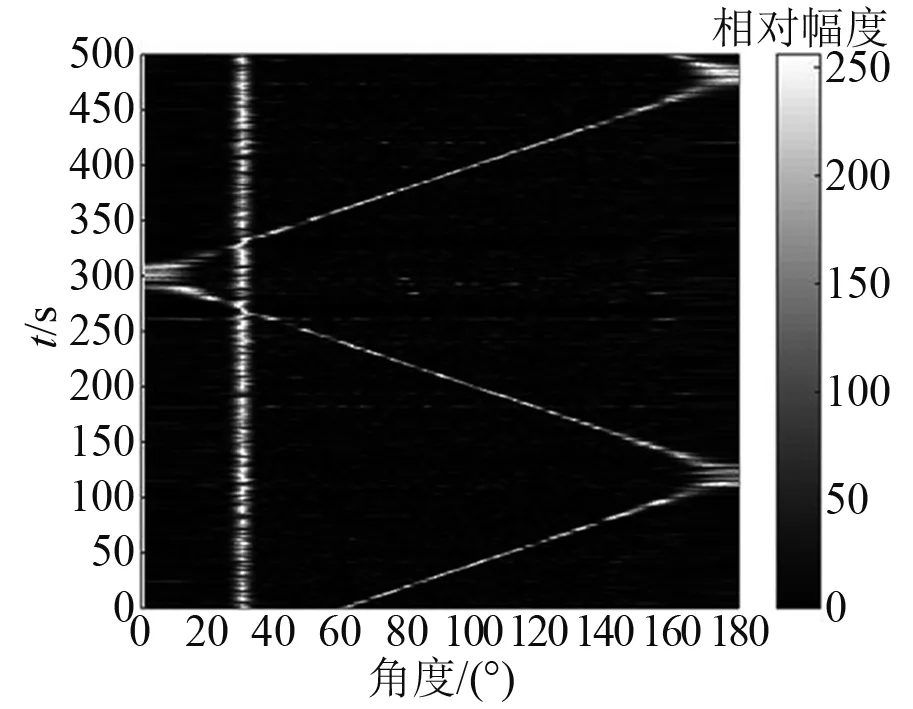
图2 本文方法输出方位历程图Fig.2 Output bearing course diagram of this method

图3 本文方法和子空间方法输出空间强度谱Fig.3 Output spatial spectrum of this method and subspace method

图4 本文方法所得的判决因子 αnThe judgment factor αn of this method
由式(5)可知,在该仿真条件下,受目标快速运动影响,一次处理数据可用帧数K1≤10,同时由式(4)可知,受目标方位估计方差限制,一次处理数据所需帧数K2>N,K2≤K1表明该仿真中数据平稳性不能满足子空间方法需求,即在该仿真中一次处理数据时间内,同一方位数据中信号的参数(目标信号方位)发生了变化,统计特性发生了变化,即通过事先划分的125帧频域数据完成协方差矩阵累积求取时,同一目标信号将被分配到两个子空间上,影响子空间方法求取协方差矩阵估计结果和空间谱估计结果。
图1~图3仿真结果也进一步验证了:相比子空间方法,本文方法对目标方位估计效果更好;子空间方法所得结果背景噪声级远高于本文方法,本文方法所得空间强度谱主副瓣比大于子空间方法所得空间强度谱主副瓣比10 dB以上,本文方法比子空间方法有更低的背景噪声级。该现象进一步说明在一次处理数据中,同一方位空间数据稳定性较差时,本文方法可以有效降低子空间方法对协方差矩阵估计所需稳定数据量,即本文方法可通过对1帧数据时域多点累积实现协方差矩阵估计,同时采用图4所示判决因子αn对各子空间空间强度谱进行了处理,在无目标先验信息情况下,可有效提升空间目标子空间强度谱在最终合成空间强度谱中的比重,降低了背景噪声对合成空间强度谱的影响。
为进一步验证本文方法对目标方位估计性能,目标信号与背景噪声平均谱级比为-30~0 dB情况下,由500次独立统计所得子空间方法与本文方法对上述仿真中60°运动目标方位估计均方根误差,如图5所示。

图5 本文方法与子空间方法所得均方根误差Fig.5 RMSE of bearing estimation of this method and subspace method
由图5仿真结果可知,对于同一方位估计均方根误差,相比子空间方法,本文方法对目标方位估计的稳健性提高了5 dB以上。
3.2 实测数据处理分析
为进一步验证本文方法对目标方位估计性能,分别利用本文方法和子空间方法对线列阵试验数据进行处理分析。试验中,接收阵相邻传感器间距为2 m,传感器数为40,等间距分布;处理数据时间长度为500 s,接收阵拾取数据所用采样率为8 kHz,一次处理数据长度为16 k个采样数据,处理数据频段为250~500 Hz。实测数据具体处理过程与数值仿真分析过程一样,处理中目标先验信息未知,图6和图7分别为子空间方法和本文方法处理所得时间历程图。图8给出了典型时刻两种方法输出空间强度谱结果。

图6 子空间方法输出方位历程图Fig.6 Output bearing course diagram of subspace method

图7 本文方法输出方位历程图Fig.7 Output bearing course diagram of this method

图8 本文方法与子空间方法输出空间强度谱(t=240 s)Fig.8 Output spatial spectrum of this method and subspace method (t=240 s)

同时,对比图6与图7可知,本文方法所得方位历程图中目标方位明晰可辨,而子空间方法在0~500 s时间段内无法对75°和90°附近目标的方位实现有效估计,进一步验证了本文方法可以有效降低子空间方法对协方差矩阵估计所需稳定数据量,即本文方法可通过对1帧数据时域多点累积实现协方差矩阵估计;同时在无目标先验信息情况下,本文方法通过对各子空间输出空间强度谱的检测指数判决处理,降低了背景噪声对最终合成空间强度谱影响。同样,由图8可知,本文方法所得空间强度谱检测指数优于子空间方法,表明本文方法比子空间方法有更低的背景噪声级。
4 结 论
针对子空间高分辨方位估计方法稳健性差的问题,首先分析了影响子空间高分辨方位估计方法的因素;然后针对影响因素,提出了一种基于检测指数判决的子空间方位估计方法。
(1) 该方法完全基于时域处理,通过一次多个时间点累积稳定获取了满秩协方差矩阵,降低了空间非稳定数据对子空间分解产生的影响。
(2) 依据空间目标在各子空间强度谱检测指数差异,对各子空间合成空间强度谱进行判决处理,降低了背景噪声对最终合成空间强度谱影响。
(3) 数值仿真及实测数据处理结果表明,相比现有子空间方法,本文方法降低了空间非稳定数据对子空间分解产生的影响,降低了背景噪声对合成空间强度谱影响,对最低信噪比的需求得到了5 dB以上的改善。

