无模型控制在气动变载荷加载系统中的应用

任丽娜， 李小广， 高琳琪， 刘福才

(燕山大学 工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

气动加载技术是一种成本低、重量轻、实用性强的工业技术。它以压缩空气为工作介质，进行能量的转换和控制，以实现机械化的生产制造[1]。当今社会，工业生产技术发展迅猛，机电一体化已成为机械制造发展的重要趋势，而其中气动加载技术所特有的无污染、性价比高、工作原理简单等特点，使得系统安全稳定[2-3]，并且在工业生产应用中加上关键部件电气比例阀后，响应速度更快，响应精度也得到了很大的提高，因此在全世界范围内得到了广泛应用[4]。

但是气动加载系统的压力跟踪控制依然是当代社会工业研究的一大难题，这其中最主要的原因自然就是气动加载系统所具有的强非线性、强耦合性。气动加载的空气特性、关键部件电气比例阀的时滞性和气缸两腔摩擦力这些原因，给气动加载系统的建模与控制器设计造成了很大的困难[5-6]。

为解决上述问题，近些年来出现了很多针对气动系统的控制策略。文献[7]提出了一种基于模糊算法的状态反馈增益整定的控制方法，这种方法可以工作在控制非线性系统和加载载荷不断变化的情况。但是，在被控对象的载荷保持恒定时就有一定的局限性。文献[8]中提到了一种多输出反馈的方法对来气动加载系统进行运动控制，并且能够对不断变化的摩擦因数进行补偿。文献[9]提出了一种自适应模糊PD(proportion differentiation)控制方法，并证明了该方法的自适应性，最后又在实际系统进行试验验证。文献[10]中提出一种称为Robust Loop Shaping-Fuzzy Gain Scheduled (RLS-FGS)的控制方法用于气动系统的控制，通过粒子群算法(particle swarm optimization，PSO)来确定实际应用的最佳参数。文献[11]通过在自抗扰控制器中增加积分环节，从而增强系统的鲁棒性。

上述的这些控制方法虽然都能在一定条件下取得不错的控制效果，但是控制器的设计都或多或少依赖于被控系统模型，而气动加载系统的建模困难与强时变性使得这些控制策略在实际应用中有很多困难。本文为实现气动加载系统的压力实时跟踪控制设计无模型自适应控制器，其中无模型控制是指在控制器的设计过程中不包含被控系统的任何数学模型信息，仅需被控系统的输入输出数据来进行控制的控制器。

1 气动变载荷加载系统的描述以及数学建模

1.1 气动变载荷加载系统的组成及工作原理

气动加载系统工作原理如图1所示。

图1 气动加载系统原理图Fig.1 Schematic diagram of pneumatic loading system

气动加载系统的组成部件包括气源、气动二联件、电气压力比例阀、气缸、拉压力传感器、上位工控机等。其中，气泵的作用是提供气源；压力传感器位于气缸和样品台之间，作用是实时的反馈加载的压力大小；然后上位机通过返回的输出压力信号与系统给定的输入信号进行作差，通过无模型自适应控制器或者经典PID控制器，产生控制信号；控制信号在模拟量输出单元转换为输出电流，电流信号控制电气比例阀的开度，最终控制气缸的实时压力输出。

1.2 气动变载荷加载系统数学模型的建立

气缸加载系统的控制原理如图2所示，图中省去了实际系统必备但与控制系统无关的空气过滤器、减压阀等气源处理单元[12]。

图2 气动加载系统控制原理图Fig.2 Pneumatic loading system control diagram

在仿真计算中，气动加载系统由于空气状态的非线性与复杂性，不能建立完整的贴近实际系统的数学模型。为了便于获取系统的输入输出数据，研究系统的实时加载特性，遂作出如下假设[13-14]：①大气压力、气源压力在一定时间内保持恒定不变； ②排气压力恒定不变； ③忽略气体的动能和势能； ④气缸与储气罐内的气体运动视为等熵绝热，保持能量守恒；⑤气体运动过程满足理想气体运动方程；⑥气缸内的气体是均匀的，整个过程不存在气体泄漏。

由牛顿第二运动定律，得到气缸运动的力平衡方程为

(1)

式中：M为活塞和负载总质量；B为黏滞摩擦因数；Fc是库伦摩擦力；Pa和Pb分别为气缸A腔和B腔的接触面积作用压强；Aa和Ab分别为气缸A腔和B腔的作用面积；Patm为环境压强；Ar为气缸杆横截面积。

MCL-ZT拉压力传感器属压阻式传感器，其输出压力F与长度形变量即气缸位移x之间呈趋势型线性关系，考虑到零位压力存在的可能性，其关系式可写为

F=Kf1x+bf1

(2)

式中：Kf1为比例系数；bf1为常数，起到调零作用。

通过电气比例阀进入气缸腔内的气体质量流量可表示为[15]

(3)

其中，

(4)

式中：Cf为流量系数；Av为电气比例阀的有效开口面积；Pu为气缸供给压强；R为理想气体常数；T为绝对温度；Wv为电气比例阀开口面积梯度；xv为电气比例阀的阀芯位移长度；k为绝热指数，取k=1.4。

电气比例阀通过电控的方式对气体流量或气动加载输出压力进行实时连续控制，因此其输入输出特性可以等效为比例环节，即

xv=Kvuv

(5)

式中：Kv为电气比例阀流量增益；uv为控制电压。

由质量守恒定律,气缸容腔流入和流出的气体质量流量和容腔的质量变化率相等,可表示为

(6)

假设气体为理想气体,满足理想气体状态方程

P=ρRT

(7)

联立式(6)和式(7)得

(8)

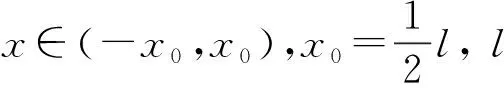
(9)

联立式(3)、式(4)、式(9)，整理可得

(10)

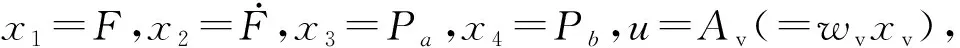
(11)

状态方程式(11)便是该气动变载荷加载系统的数学模型，设计该气动摩擦系统数学模型仅是为了产生系统仿真研究所用的I/O数据，并不参与控制器的设计。

2 无模型自适应控制器设计

2.1 无模型自适应控制器的基本概念

无模型自适应控制(model free adaptive control, MFAC)是侯忠生教授在其博士论文中提出的。该方法引入一个新的概念，伪梯度向量(或伪Jacobi矩阵)和伪阶数，在被控系统的轨线附近用一系列的动态线性时变模型来近似替代一般的非线性系统，仅用被控系统的输入输出数据在线估计系统的伪梯度向量。其中的基于紧格式线性化和偏格式线性化的MFAC方案已经给出了在一些假设条件下的收敛性和稳定性的理论证明[16-19]。这种控制器参数少，易于实现，因此一经提出便得到了飞速发展。目前在化工制造、电机控制、城市道路交通控制、板形控制等多种行业进行了应用，并且获得了中国技术发明专利。仿真和理论研究、实际工业应用都从多个方面证明了MFAC能够解决被控系统中的强非线性和时变性等控制难题。

2.2 一般离散时间非线性系统的紧格式线性化方法

考虑一类SISO离散时间非线性系统

y(k+1)=
f(y(k),…,y(k-m),u(k),…,u(k-n))

(12)

式中：y(k)，u(k)分别为系统的输出与输入；m,n为系统的阶数。

对于式(12)，做出以下假设[20]：

假设1系统式(12)是可观可控的。即对于有界的期望信号y*(k+1)，存在有界的控制输入信号。

假设2f(…)关于系统的控制输入信号u(k)的偏导数是连续的。

假设3系统式(12)是广义Lipschitz的，即满足对任意时刻的k和Δu(k)≠0有

|Δy(k+1)|≤b|Δu(k)|

(13)

式中： Δy(k+1)=y(k+1)-y(k)； Δu(k)=u(k)-u(k-1)；b为常数。

由此可得以下定理：如果可以同时满足以上三个假设条件，那么当Δu(k)≠0时，一定存在一个伪偏导数φ(k)使得系统可以用式(14)来表示

y(k+1)-y(k)=φ(k)Δu(k)

(14)

式中， |φ(k)|≤b，φ(k)为y(k+1)关于u(k)的梯度，能够变化而实现自适应部分。

2.3 基于紧格式动态线性化的无模型自适应控制方案

上面所给出的线性化方法与传统的线性化方法有着很大的不同。为了能够控制动态折线化近似在合理的范围内，考虑如下的控制输入准则函数

J(u(k))=[y*(k+1)-y(k+1)]2+
λ[u(k)-u(k-1)]2

(15)

式中：λ为线性化权重因子；y*(k+1)为k+1时刻系统的给定值。λ[u(k)-u(k-1)]2可以限制输入量的变化，并且可以克服稳态跟踪误差。将式(12)代入式(13)中对u(k)进行求导，令其等于零，则

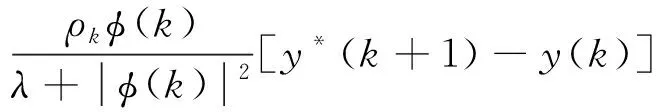
(16)

式中，ρk为步长序列。

控制算法中加入权重因子λ的作用有两个。一是限制非线性系统线性替代的范围，因此也间接的限制了伪偏导数的变化；其次，权重因子避免了式(16)中分母为零的情况。

以上算法中，k时刻唯一不知道的参数就是伪偏导数的值。下面将采用参数估计算法，进行伪偏导数φ(k)的估计。伪偏导数估计准则函数

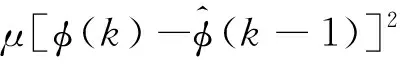
(17)

式中：y*(k)为k时刻系统的输出值；μ为权重因子。 对φ(k)进行求导并令其等于零，得到如下伪偏导数估计算法

(18)

式中，ηk为步长序列。

根据上面的参数估计算法以及控制律算法得出MFAC控制方案为[21]

(19)

(20)

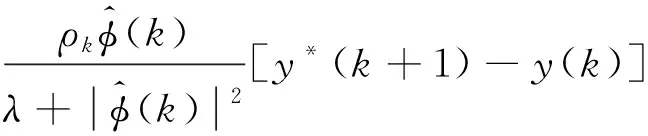
(21)

通过控制方案式(19)～式(21)可以看出，该控制器的设计仅需被控系统的输入输出数据，不显含或隐含任何关于受控系统动态模型的信息。由于伪偏导数φ(k)对时变参数、时变结构的不敏感，因此无模型自适应控制方案具有非常强的适应性和鲁棒性，传统的基于被控系统数学模型的控制方案设计很难达到这一点。

3 仿真与实验研究

3.1 仿真研究

在MATLAB软件中进行仿真研究，并在三种典型输入信号下将MFAC与PID控制器的控制效果进行对比。其中系统的部分物理参数标称值如表1所示，与Sorli等的研究相比，此次实验所用到的气缸内腔横截面积更大。

表1 气动加载系统物理参数标称值Tab.1 Nominal value of physical parameters of pneumatic loading system

在压力给定为恒值500 N时，MFAC和PID控制系统的压力跟踪曲线和误差曲线分别如图3和图4所示。由图可以看出，给定恒值信号加载时，系统在PID控制下稳定速度慢，峰值误差大，且一直存在震荡；而在MFAC控制下，跟踪速度快，抖振现象小，跟踪误差迅速趋于零，跟踪性能良好。

图3 恒值加载压力跟踪曲线Fig.3 Constant loading pressure tracking curve

图4 恒值加载压力误差曲线Fig.4 Error curve of constant loading pressure

在给定峰值为600 N，周期为12 s的正弦波信号时， 两种控制器的跟踪曲线和误差曲线分别如图5和图6所示。由图可以看出，在PID控制下系统存在一定的滞后与抖振，且存在震荡现象；而在MFAC控制下，系统压力无滞后，在波峰处误差小，系统稳定，跟踪性能良好。表明MFAC对正弦波信号具有良好的跟踪效果，抗干扰能力强。

图5 正弦波加载压力跟踪曲线Fig.5 Sinusoidal load pressure tracking curve

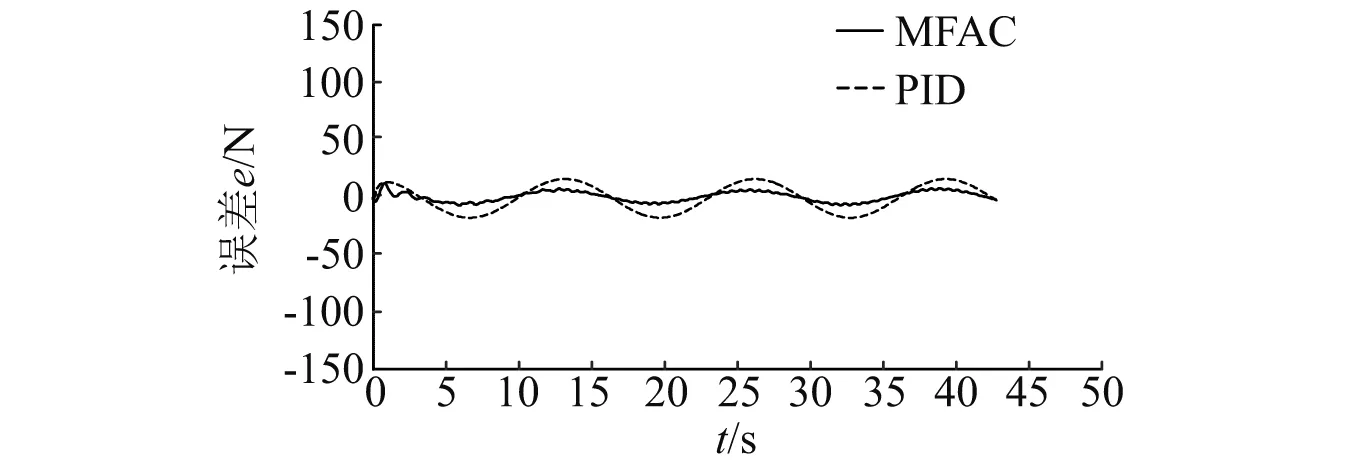
图6 正弦波加载压力误差曲线Fig.6 Error curve of sinusoidal loading pressure

在压力给定峰值为600 N，周期为10 s的方波加载时，两种控制器的跟踪曲线和误差曲线分别如图7和图8所示。由图可以看出，在给定信号为方波信号时，PID控制的系统存在较大误差，且在峰值处存在明显的震荡现象；而在MFAC控制下，系统峰值处抖动误差较小，输出信号较平滑，跟踪性能较好。

图7 方波加载压力跟踪曲线Fig.7 Pressure tracking curve of square wave loading

图8 方波加载压力误差曲线Fig.8 Error curve of square wave loading pressure

3.2 实验验证

为验证无模型自适应控制器在实际应用中的有效性，在实际系统上进行实验，该试验机可以实现数值连续可变的变载荷加载，实物如图9所示。控制算法式(17)～式(19)采用VC++语言实现。并对无模型自适应控制和经典PID控制的控制效果进行对比分析。

图9 气动变载荷加载试验机Fig.9 Pneumatic variable load loading testing machine

给定峰值为600 N的恒值信号,将PID闭环控制和MFAC的参数都调至最优，PID参数为kp=1.01，ki=3，kd=1.1，MFAC参数为λ=1，μ=0.2，ρ=1，η=1。两种控制器下的加载曲线和误差曲线分别如图10和图11所示。由比较可知，系统在PID控制下的恒值加载中一直存在震荡，有较大滞后，且波动误差大；而在MFAC控制下，系统滞后小，跟踪迅速，整体曲线平稳，跟踪性能良好。

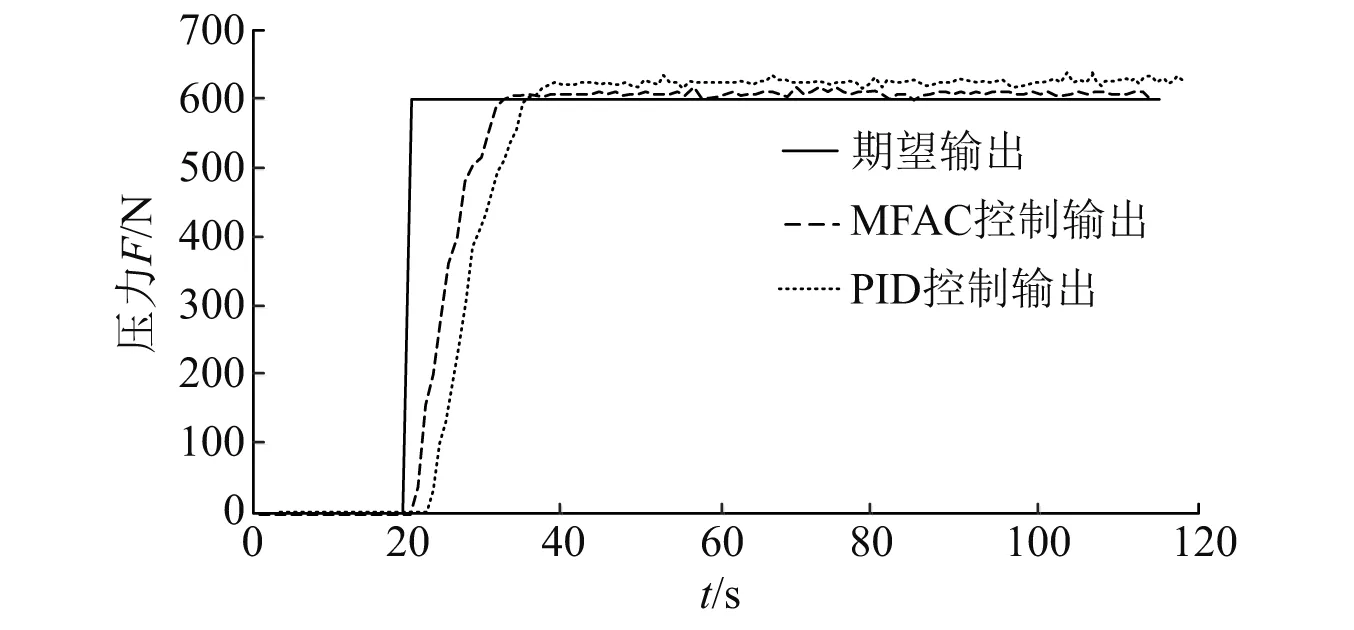
图10 恒值加载试验跟踪曲线Fig.10 Constant loading test tracking curve

图11 恒值加载试验误差曲线Fig.11 Error curve of constant loading test

PID闭环控制和MFAC控制下的正弦波加载曲线和误差曲线分别如图12和图13所示。当给定峰值为500 N，周期50 s的正弦波信号时，将两种控制器的参数都调至最优，PID参数为kp=4，ki=1.2，kd=0.5，MFAC参数为λ=0.5，μ=0.1，ρ=0.5，η=1。观察图12和图13可知，在PID控制下系统存在明显的抖振和滞后，且存在震荡现象，峰值误差大；而在MFAC控制下，系统压力跟踪较为平滑，峰值误差小，跟踪速度较快，系统稳定，抗干扰能力较强。

图12 正弦波加载试验跟踪曲线Fig.12 Sinusoidal loading test tracking curve

图13 正弦波加载试验误差曲线Fig.13 Error curve of sinusoidal loading test

PID闭环控制和MFAC控制下的系统的方波加载曲线和误差曲线分别如图14和图15所示。当给定峰值500 N，周期50 s的方波信号时，将控制器参数调至最优，其中PID参数为kp=0.5，ki=1.5，kd=0.5，MFAC参数为λ=5，μ=0.1，ρ=1，η=1。观察加载曲线和误差曲线，在PID控制下系统峰值误差大，有滞后；而在MFAC控制下，系统压力跟踪较好，整体误差比PID误差小，系统稳定，抗干扰能力较强。

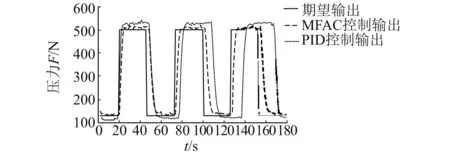
图14 方波加载试验跟踪曲线Fig.14 Square wave loading test tracking curve

图15 方波加载试验误差曲线Fig.15 Error curve of square wave loading test

4 结 论

(1) 本文为解决气动加载系统的控制精度低、跟踪性能差等问题,设计了无模型自适应控制器，这种控制器易于应用、计算简便、适合气动加载系统这种无法精确建模的控制对象。并且在MATLAB进行了仿真研究，对比经典PID控制，仿真结果表明在三种典型的输入信号下，MFAC具有更强的适应性和鲁棒性。

(2) 在气动变载荷摩擦磨损试验机上进行实验验证，用Visual Studio平台编写离散化控制程序，验证了给定为三种典型的输入信号下，无模型自适应控制器和经典PID控制器的跟踪效果。通过分析试验曲线可知，无模型自适应控制器在三种输入信号下均能保持响应速度快、控制精度高的优点。