基于模糊非支配排序遗传算法的多车型快速路交通拥堵和排放优化

陈 娟， 荆 昊， 孙向阳

(上海大学悉尼工商学院， 上海 201899)

城市快速路系统是承担城市长距离与大运量交通的主骨架道路系统， 其运行服务水平的优劣直接影响着城市道路交通的效能.上海等城市快速道路的拥挤乃至阻塞问题日趋严峻[1].与此同时， 城市快速路的进出口匝道也与主路的通行效率关系密切.在匝道进出口区域对汇入车辆进行主动管理与控制， 可以减少匝道汇入区对主路交通的影响， 提高快速路的通行效率，同时减少因交通阻塞造成的低速行驶所增加的汽车尾气排放和燃油消耗.相关研究显示， 这些汽车尾气污染物是造成城市雾霾的主要因素之一[2].

本研究在对多车型快速路交通流基本特性和交通管理与控制理论深入总结的基础上， 将同时考虑了交通拥堵和环境影响的多车型快速路优化问题描述为高维多目标优化问题， 把快速路的走行时间(total time spent， TTS)、走行距离(total travel distance， TTD)、匝道排队、燃油消耗和尾气排放这5 个指标作为高维多目标遗传算法的优化目标， 对快速非支配排序遗传算法(non-dominated sorting genetic algorithm， NSGA-Ⅲ)[3]进行了改进， 提出了模糊非支配排序遗传算法(fuzzy NSGA-Ⅲ， FNSGA-Ⅲ)， 并对上述问题进行求解.引入并修改了多车型宏观交通流模型Multi-class METANET 与多车型排放油耗模型Multi-class VT-macro[4]， 选取了上海市的实际快速路段数据， 对Multi-class METANET 模型的参数进行拟合.采用本研究提出的FNSGA-Ⅲ算法， 同时优化了多车型快速路系统的可变限速值与匝道控制率， 以实现减少快速路交通拥堵、匝道排队与油耗排放的目标.

交通领域的优化问题通常具有多维属性， 一般需要同时优化多个交通指标， 其实质是多目标优化问题.解决该问题的主要方法之一是多目标进化算法(multi-objective evolutionary algorithms， MOEAs)[5].已有多种方法对MOEAs 进行改进， 可使其能更好地解决高维空间优化问题， 如对问题降维、占优机制优化等， 其中基于分解的方法是研究热点之一[6]， 即基于参考点或者参考向量的MOEAs 方法[7].这类MOEAs 方法能够产生一组均匀分布在高维空间中的参考点， 将高维空间拆解， 分为多个子空间， 同时优化多个子空间的子种群， 从而有效解决算法在高维空间中Pareto 解的选择压力问题.因此， 本研究基于参考向量来提高Pareto 解的质量和算法的收敛度， 在NSGA-Ⅲ算法[3]的基础上， 引入了模糊逻辑推理算法， 对Pareto 解的超平面进行预测， 解决了以往算法对超平面难以确定的问题.

交通流模型与控制策略是解决各类交通问题的理论基础和实施手段.宏观交通流模型中METANET 模型[8]对路网真实情况的刻画最为精确.为了解决多车型情况下交通流模型的刻画问题， Shuai等[4]提出了基于多车型的Multi-class METANET 模型与Multi-class VT-macro 模型， 并结合多车型排放模型VT-macro[9]， 来避免因不同类型车辆特性不同而造成的尾气排放和燃油消耗的估算误差.但是文献[9]没有考虑匝道汇入车辆的排放.

可变限速(variable speed limit， VSL)与匝道控制是目前最常用的交通控制策略.VSL 提前给予驾驶员动态的限速建议; 匝道控制决定了匝道允许放行的车辆数， 均衡交通负荷， 提升路网运行效率[10].在以往的单车型快速路优化控制问题中， 这两种策略往往集成考虑.Li等[11]将VSL 策略集成到单车型元胞传输模型(cell transmission model， CTM)模型中， 利用VSL 对快速路主路进行控制， 优化路网中的行程时间.Iordanidou等[12]设计了一种可以协调多入口匝道的匝道控制器， 并且集成VSL， 但其控制算法较为简单且目标维数较少.模型预测控制方法在解决多车型快速路优化问题中有很重要的地位.Pasquale等[13]考虑了小汽车与重型卡车两种车型， 提出了采用模型预测控制方法来实现交通安全和排放的优化， 但也仅仅考虑了两个目标的线性加权， 而且只采用了匝道控制策略.

综上所述， 已有研究在采用模型预测控制方法来处理多个交通性能指标时， 通常是采用简单的线性加权， 难以进行多个目标之间较好的协调.在考虑多车型模型这种较为复杂的情况下， 线性加权的局限性就更为突出.本研究设计了FNSGA-Ⅲ算法， 结合模糊逻辑推理与快速NSGA-Ⅲ算法， 通过算法运行中保留的历史进化信息， 对多输入多输出模糊推理系统进行了训练.然后基于训练生成的模糊推理系统， 对算法生成的超平面进行预测， 引导算法进化方向， 从而更有效地解决了多车型环境下， 同时考虑多个性能指标的交通拥堵与排放的优化问题.

1 高维多目标优化算法

1.1 多输入多输出的模糊推理系统

自适应模糊推理系统(adaptive network-based fuzzy inference system， ANFIS)[14]是在自适应神经网络框架下实现的模糊推理系统.ANFIS 作为一种非线性建模方法， 可以通过使用多层学习过程， 识别控制系统中的非线性分量， 用于非线性控制.此外， ANFIS 结合了模糊理论与非线性系统的数学理论， 参数易于调整、扩展到多输入多输出的模糊系统中.ANFIS 主要包含模糊规则、隶属度函数等部分， 单输入单输出ANFIS 的过程如图1 所示.

图1 单输入单输出ANFISFig.1 Single input single output ANFIS

本研究需要实现基于模糊推理的高维多目标优化算法的超平面预测问题， 本质上需要解决多输入多输出ANFIS 建模的问题.本研究在文献[14]提出的双输入双输出ANFIS 的基础上， 拓展得到了多输入多输出ANFIS， 其过程描述如下: 定义单输入单输出的一组模糊规则为一个模糊规则集合; 由多个单独的模糊规则集合构成模糊规则森林; 在模糊规则森林中， 每个单独的模糊规则集合产生其输入对应的输出值; 最终通过并联多个模糊规则集合， 实现多输入多输出ANFIS 的建模.

图2 描述了本研究拓展后的多输入多输出ANFIS.输入1～n代表输入的n个向量.通过不同的模糊规则集合， 对不同的向量进行模糊推理， 获得该向量对应的输出规则.之后对该输出规则内的输出进行线性加权， 获得与该向量对应的输出1～n.具体可分为如下5 层:①对n组输入进行模糊化， 生成对应的n组隶属度函数; ②在组内将隶属度函数相乘， 输出代表其规则的激发强度代数积; ③在组内计算第i个规则的激发强度与所有规则的激发强度之和的比率; ④计算各组内各个节点的输出; ⑤对各组内各个节点的输出进行加权平均， 即为当前组的最终输出.

图2 多输入多输出ANFISFig.2 Multiple input multiple output ANFIS

在本研究提出的多输入多输出ANFIS 的基础上， 对NSGA-Ⅲ算法[3]中下一时刻的超平面进行预测.通过算法运行中保留的进化信息， 以及多次运行该算法后保存的往期最优解集， 对多输入多输出ANFIS 进行训练， 生成本FNSGA-Ⅲ算法中采用的多输入多输出ANFIS.对下一代的参考超平面进行预测， 生成指导种群Gt.将包含往期进化信息的指导种群Gt作为参考点生成依据之一， 预估算法的进化方向， 增加算法的进化压力， 提高算法的收敛性.

1.2 基于超平面模糊推理预测的遗传算法FNSGA-Ⅲ

1.2.1 NSGA-Ⅲ

Deb等[3]提出了基于参考点的非支配解排序遗传算法NSGA-Ⅲ， 用来解决高维空间的多目标优化问题.NSGA-Ⅲ重点改进了NSGA-Ⅱ[15]中的选择算子， 基于一组均匀分布的参考点进行解的选择， 降低了算法时间复杂度， 提高了种群多样性.本研究的改进思路如下: 在非支配解集中， 尽可能多地包含更优解， 以供算法进行解的选择; 同时设置更加合理的参考点来加速算法的收敛.本研究提出的FNSGA-Ⅲ算法对文献[3]中提出的参考超平面方法进行了改进.参考超平面的生成包含了更多的进化信息， 提高了参考超平面的效率.

1.2.2 FNSGA-Ⅲ

图3 给出了本研究提出的FNSGA-Ⅲ算法的流程图， 其主体框架步骤描述如下.

图3 FNSGA-Ⅲ算法流程图Fig.3 Flowchart of FNSGA-Ⅲalgorithm

输入H个参考点组成的未标准化的参考点集合Zs、最大迭代次数gen、当前种群Pt.

输出 下一代种群Pt+1.

步骤1 对算法的参数、种群进行初始化设置， 种群大小N， 时间窗t= 1， 随机产生初始种群P1， 非支配解集St=∅.

步骤2 对种群Pt进行重组、交叉和变异， 生成子代种群Qt，Qt=Recombination(Pt)+Mutation(Pt).

步骤3 调用子算法2， 训练并生成多输入多输出模糊系统FisMat.调用子算法3， 采用多输入多输出模糊系统FisMat 来产生指导种群Gt，Gt=mimo-ANFIS(Pt).

步骤4 合并父代种群Pt、子代种群Qt与指导种群Gt， 生成合并种群Rt，Rt=Pt ∪Qt ∪Gt.

步骤5 对合并种群Rt执行非支配排序操作， 产生非支配解集Rt={F1，F2，··· ，Fl，···};对非支配解集R进行非支配排序，得到集合U，Ut=Non-dominated-sort(Rt)，其中F1，F2，··· ，Fl，···分别表示Rank 等级为1，2，··· ，l，···的非支配解集，F1≻F2≻F3···≻Fl···.

步骤6 生成非支配解集St， 具体过程如子算法4 所示.

步骤7 生成下一代种群Pt+1.如果St中解的个数恰好等于N， 即当|St|=N时， 则直接生成下一代父代种群Pt+1，Pt+1=St， 并且t=t+1， 返回步骤2.否则， 由F1，F2，··· ，Fl-1组成部分Pt+1， 即Pt+1=l-1∪j=1Fj， 剩余的K个解需要从第Fl层中根据小生境计数进行筛选得到，即种群Pt+1需要从Fl中挑选出的解的数目K=N -|Pt+1|.

步骤8 生成参考点， 生成方法如子算法5 所示， 产生参考点集合Zr=Normalize(fn，St，Zs，Zr).

步骤9 将非支配解集St中的解与参考点进行关联，具体步骤参考文献[14]，即[π(s)，d(s)]=Associate(St，Zr)， 其中π(s)表示最近的参考点，d(s)表示s与π(s)的距离.

步骤10 计算属于参考点集合Zr内每个参考点j的小生境计数.根据小生境计数选择K个元素来构建种群Pt+1， 从Fl中选择K个解加入种群Pt+1.小生境计数的具体方法参考文献[3].

步骤11 令t=t+1， 返回步骤2.当t=gen 时， 输出最后的解集Pfinal.

1.2.2.1 子算法2: 多输入多输出模糊系统FisMat

子算法2 将FNSGA-Ⅲ算法中每一代产生的父代种群， 以及该算法多次运行时保存的最优解集合并作为模型的输入， 训练并生成多输入多输出模糊系统FisMat.子算法2 的步骤描述如下.

输入 训练集包括第1 代到第t-1 代的父代种群{P1，P2，··· ，Pt-1}、算法多次运行保存的最优解集合Pastset{D}， 其中Pastset{D}是算法在多次运行中产生的30 组种群数为100 的最优解集合.测试集包括Pt、目标维数m、种群数pop.

输出 多输入多输出模糊系统FisMat.

步骤1 提取所需数据作为算法输入.

步骤2 数据归一化处理， 生成归一化后值在(0， 1)内的新矩阵Pinput.

步骤3 确定输入变量的隶属度函数.经尝试， 本研究的隶属度函数个数定义为3， 采用高斯型隶属度函数.

步骤4 生成初始化模型， 设置训练代数、训练步长、输出区间.

步骤5 到达最大训练代数后， 获得训练完毕的多输入多输出模糊系统FisMat.

1.2.2.2 子算法3: 生成指导种群Gt

子算法3 用来生成指导种群Gt， 具体步骤描述如下.

输入 第2 代到第t代的父代种群{P2，P3，··· ，Pt}、算法多次运行保存的最优解集合Pastset{D}、目标维数m、种群数pop、多输入多输出模糊系统FisMat.

输出 指导种群Gt.

步骤1 提取所需数据作为算法输入.

步骤2 判断是否为初代种群: 若不是， 则根据生成的模糊系统FisMat， 基于子算法2， 产生指导种群Gt， 转步骤3; 若是， 令Gt=∅， 转步骤3.

步骤3 将父代种群Pt、子代种群Qt与指导种群Gt合并，形成合并种群Rt=Pt∪Qt∪Gt.

1.2.2.3 子算法4: 生成非支配解集St

子算法4 用来生成非支配解集St， 具体步骤描述如下.

输入 非支配解集{F1，F2，··· ，Fl，···}、初始化非支配解集St= ∅、种群中的个体数目N、计数器i=0.

输出 非支配解集St， 最后一次加入到St中的解的非支配等级Fl.

步骤 依次将F1，F2，··· ，Fl，···并入St中，St=St ∪Ft.每完成一次， 计数器加1，即i=i+1， 直到St中的解集数目大于或等于N为止， 即|St|≥N.最后一次加入到St中的个体的非支配等级Fl为Fl=Fi.

1.2.2.4 子算法5: 生成参考点集Zr

子算法5 用来对合并种群Rt进行归一化， 生成一组参考点集Zr.在原有的NSGA-Ⅲ中，第t代的参考平面生成方法仅仅基于父代种群Pt和子代种群Qt， 只考虑了上一代的进化信息， 忽略了t代前Pareto 超平面的进化趋势.本研究结合{P1，P2，···Pt}种群和历史最优解集合Pastset{D}， 采用ANFIS 进行超平面预测， 得到了一组指导种群Gt.将Pt，Gt与Qt合并，形成新的种群Rt.子算法5 的具体步骤描述如下.

输入 非支配解集St，H个参考点组成的未标准化参考点集合Zs.

输出 标准化后的参考平面fn， 标准化后的参考点集合Zr.

步 骤1 从1 到目 标 维 数m首 先 计算理 想 点=fj(s)，j= 1，2，··· ，m， 其中表示第j个理想点，fj(s)为第j列解向量.然后进行坐标转换， 对解集St内的任一解s，减去其对应列的理想点值最后计算极端点:其中表示第j个极端点.

1.2.3 解的选择采用高维多目标优化算法进行求解时， 会面临如何选取最优解的问题.最优解的选取需要结合实际问题， 根据需要来选择更加偏重的指标.基于本研究提出的FNSGA-Ⅲ算法， 每次运行会得到多个Pareto 最优解.本研究采用文献[16]提出的逼近理想解排序法(technique for order preference by similarity to ideal solution， TOPSIS)进行解的选择， 并在结果分析中对各结果进行了详细对比.

2 多车型交通流模型与排放油耗模型

2.1 多车型交通流模型与排放油耗模型

本研究主要参考了Shuai等[4]提出的Multi-class METANET 模型与Multi-class VT-macro模型.与原模型相比， 改进后的模型更加符合本研究采用的实际快速路路网现状.

本模型的第一个改进之处在于: 在考虑拥堵和不拥堵时分别采用了不同的期望速度， 即对当前密度是否超过路段临界密度进行了判断， 针对不同情况采用了不同的期望速度计算公式.考虑到本研究采用的上海市快速路的实际情况， 设置临界密度约束作为是否实施速度控制的依据.改进后的期望车速公式为

本模型的第二个改进之处有如下两点.第一， 在文献[8]模型基础上， 对匝道控制策略进行改进， 设置了基于不同车型的不同放行比例， 并且计算了匝道部分的尾气排放与燃油消耗.在匝道方面，c型车允许从匝道进入主路的车流量ri，c(k)为

式中:μi，c(k)表示允许通过的比例， 取值范围为[0， 1].

在原有的多车型交通流模型中， 没有充分考虑匝道的汇入情况.本模型对大小车的匝道汇入进行控制， 实际可以从入口匝道进入主路的车流量为

式中:li，c(k)表示匝道排队长度， 其公式为

匝道车流量qi，c(k)的计算公式为

式(3)～(5)中:c=1，2;i=1，2，··· ，N;k=1，2，··· ，K-1.

第二， 在Multi-class VT-macro 模型[4]中， 并未涉及匝道速度的预测模型.为了计算匝道的时空加速度， 本模型将基于匝道的平均速度值用来估计匝道的时空加速度[9].若以时间加速度为例， 则路段i在k时刻车辆的尾气排放量(见式(6))与燃油消耗(见式(7))为

式中:

下标y ∈{CO，HC，NOx，FC}， 其中FC 为燃油消耗的简称;Py，c为c型车的参数矩阵.匝道部分的尾气排放Jon，emission，c(k)与燃油消耗Jon，fuel，c(k)在k时刻分别为

式中: 下标on 表示入口匝道编号;c表示入口匝道的c型车.

2.2 高维多目标优化问题描述

本研究选取的性能指标是走行时间(TTS)、走行距离(TTD)[17]、尾气排放、燃油消耗和匝道排队.TTS 与TTD 用来衡量路网效率; 尾气排放与燃油消耗用来评价环境效益; 匝道排队用来反映匝道的通行能力和拥堵程度[17].

将改进后的Multi-class METANET 模型和Multi-class VT-macro 模型作为预测模型， 使得多车型快速路的交通优化控制问题可被描述为如下的高维多目标优化问题.

(1) 走行时间(TTS): 路网中车辆的总行程时间与入口匝道车辆排队等待时间， 即

(2) 走行距离(TTD): 所有车辆在路网中的行驶里程总和， 即

(3) 尾气排放: 所有车辆产生的尾气总量， 即(4) 燃油消耗: 一定时间内所有车辆通过路网时所消耗的燃油总量， 即

(5) 匝道排队: 在入口匝道处排队的车辆数， 即

3 仿真实例

3.1 仿真路网

以上海市广中路的一段道路作为本研究的基础路网.图4 为该路网的示例图， 主路总长4.8 km， 共计3 个匝道(1 个出口匝道， 2 个入口匝道).为了便于模拟路网的交通状态， 本研究将该路网划分为12 个路段， 每个路段长度为400 m， 如图4 所示， 其中虚线即为划分方式， 路段6、路段7 和路段12 由三车道变为两车道.

图4 快速路结构图Fig.4 Structure of the expressway

3.2 基于模糊推理系统的超平面预测

本研究训练模糊系统的步骤如下: ①输入的训练集为本次运行过程中t代前的所有解集{P1，P2，··· ，Pt-1}， 算法之前运行时得到的30 组最优解集合Pastset{D}; ②输出本次第t代解集Pt， 通过训练生成的模糊系统FisMat; ③在执行预测步骤时， 多输入多输出ANFIS 输入的是第2 代至第t代的所有解集{P2，P3，··· ，Pt}， 算法之前运行时得到的30 组最优解集合Pastset{D}， 输出为指导种群Gt.

表1 给出了模糊系统在200 代训练完成后， 训练集和测试集的均方误差(mean square error， MSE)、误差标准差(estimated standard deviation， ESD)和误差均值(mean error，ME).图5 给出了训练集在200 代训练过程中每一代的均方根误差(root mean squared error， RMSE)趋势图.由图5 可见: 模糊系统在90 代之前的RMSE 有明显减少， 从0.000 75 下降至0.000 6 左右; 之后RMSE 下滑趋势减弱， 基本保持平稳; 在200 代时RMSE 基本稳定在0.000 58 左右.这一结果表明， 模糊推理算法在收敛速度较快的同时， 也可以保证预测结果的精确度， 因此可以采用模糊预测进行较为准确的超平面预测.

表1 训练集与测试集的MSE， ESD， METable 1 MSE， ESD and ME of the training set and the testing set

图5 200 代RMSE 变化趋势Fig.5 RMSE tendency for 200 generation

3.3 路网参数标定

本研究采用分时段标定的方法对改进后的Multi-class METANET 模型参数进行标定.模型参数如表2 所示.

表2 交通流模型分时段参数Table 2 Time-phased parameters of the traffic flow model

3.4 路网概况与模型参数

为便于实施仿真和结果分析， 仿真路网中的车辆比例设置为80%小车与20%大车， 且假设驾驶员对于下发控制的遵守率为100%.仿真时长6 h， 采样周期T为10 s， 控制周期kT为5 min.图6 为2008 年9 月21 日广中路主路和两个入口匝道5:00—11:00 共6 h 内每20 s 的实际车辆需求量.

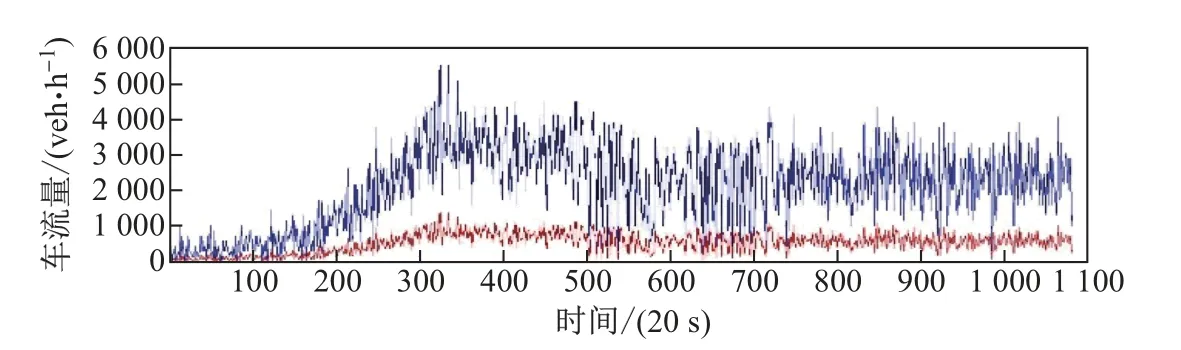
图6 主路的车流量需求Fig.6 Traffic demand on the main road

图7 和8 为广中路两个入口匝道的需求.总体来说， 两个入口匝道的车辆需求小于主线.图9 为5:00—11:00 出口匝道的分流比率.分流比率根据路网的实际数据对出口匝道的驶出率进行标定， 用来表示该时段内车辆驶离主干道的比率.出口匝道数据采集的时间间隔也为20 s，分流比率最小为0， 最大为1.

图7 入口匝道1 的车流量需求Fig.7 Traffic demand on the on-ramp 1

图9 出口匝道的车辆分流比率Fig.9 Vehicle split ratio on the off-ramp

在交通控制策略方面， 本研究对入口匝道1 和入口匝道2 进行了控制， 即控制匝道进入主路的车辆比例， 同时对主路的路段4 和路段5、路段6 和路段7、路段8、路段9 和路段10、路段11 和路段12 分别进行了VSL 控制.结果发现: 路段4 和路段5 出现车道减少情况; 路段6 和路段7 出现入口匝道1 车辆汇入情况; 路段8 出现入口匝道1 车辆汇入及车道减少情况;路段9 和路段10 出现入口匝道2 车辆汇入情况; 路段11 和路段12 出现入口匝道2 车辆汇入及车道减少情况.因此， 需要对以上主路路段进行速度控制来缓解拥堵.在本研究中， 小车的VSL 区间设置为[70， 90]， 大车为[50， 70]， 匝道进入率控制区间均为[0， 1].

图8 入口匝道2 的车流量需求Fig.8 Traffic demand on the on-ramp 2

3.5 算例仿真与结果分析

表3 给出了本研究所使用的3 种优化算法下的TOPSIS 权重表.本研究包含的3 种权重分类如下: ①单目标算法下的运行结果， 对应方案1～方案5; ②NSGA-Ⅲ算法在5 个性能指标权重均为0.2 的情况下的运行结果， 对应方案6; ③FNSGA-Ⅲ算法在多种TOPSIS 方案(即多种权重组合)下的运行结果， 对应方案7～方案18.本研究采用TOPSIS 设计方案的具体描述如下: ①方案1～方案5 是仅仅考虑单目标算法情况， 此类方案主要测试在单目标优化情况下最优解的选取情况; ②方案6 为NSGA-Ⅲ算法的均衡情况， 5 个性能指标权重均为0.2; ③方案7 为FNSGA-Ⅲ算法的均衡情况， 5 个性能指标权重均为0.2; ④方案8～方案12 为FNSGA-Ⅲ算法侧重单一目标， 同时兼顾其他4 个目标的情况; 此类方案着重考虑一个性能指标， 测试在考虑主要目标与次要目标情况下解的选取方式; ⑤方案13～方案14 是侧重2 个目标， 同时兼顾其他3 个目标的情况， 方案13 偏重TTS 和TTD， 方案14 偏重燃油消耗和尾气排放; ⑥方案15～方案16 着重考虑其中3 个目标的情况， 将匝道排队分别作为优先考虑的第3 个性能指标， 即在考虑匝道通行效率的情况下， 分别偏重主路通行效率或者环境指标时解的选取方式; ⑦方案17～方案18 为着重考虑其中4 个目标的情况， 分别把TTD 与TTS 作为次要考虑目标.因为TTD 与TTS 这两项指标在算法的优化逻辑中具有一定的冲突性， 因此方案17～方案18 主要测试算法在应对冲突目标情况下解的选取方式.

表3 18 种TOPSIS 权重选取方案Table 3 18 TOPSIS weight selection scheme

表4 给出了各TOPSIS 方案下不同优化算法的解的选取情况.结果发现， 方案7 是在各个性能指标权重均衡的情况下， 应用FNSGA-Ⅲ算法得到的解， 因此将方案7 作为对比的基础方案.在本研究所采用的5 个性能指标中， TTD 越大越优， 剩余4 项指标越小越优.本研究对如下3 种情况进行了比较: ①单目标优化算法和两种多目标优化算法结果的比较; ②两种多目标优化算法结果的比较; ③FNSGA-Ⅲ中不同TOPSIS 方案结果的比较.

表4 各TOPSIS 选取方案下的目标值Table 4 Target values under different TOPSIS selection schemes

(1) 对比了方案1～方案5， 在单目标优化情况下得到的解的差异很大.方案1 和方案2 偏重环境指标: 方案1 偏重考虑的燃油消耗指标减少了0.80%， 但是尾气排放和匝道排队指标有少许增加; 方案2 偏重尾气排放， 排放指标减少了10.67%， 但TTS 和匝道排队指标增加了10%以上， TTD 指标也减少了近9%， 即为了保证了尾气排放指标的优化， 其他指标付出较大牺牲.方案3 偏重匝道排队， 指标相比均衡情况改善近一倍， 但同时TTS、尾气排放和燃油消耗指标大幅增加.方案4 偏重TTS，在优化TTS 的同时，其他4 项指标均小幅受损.方案5 偏重TTD， 在TTD 指标大幅增加的同时， TTS、尾气排放和燃油消耗指标牺牲巨大.总体来看，在单目标优化的情况下， 偏重TTD 与匝道排队指标会带来较为极端的选解情况， 偏重指标大幅改善的同时， 会带来其他指标的大幅牺牲， 不符合实际情况需要.

(2) 在权重同为0.2 的TOPSIS 方案下， NSGA-Ⅲ算法在匝道排队指标上略好于FNSGA-Ⅲ算法， 但是TTD， TTS， 尾气排放和燃油消耗指标均略低于FNSGA-Ⅲ算法， 无法收敛至均衡情况下更优的解.特别是TTS 指标表现较差， 相比于FNSGA-Ⅲ算法多耗费了7.55%.

(3) 对比了方案8～方案12.方案8 偏重TTD， TTD 指标相比于均衡情况增加了3.71%，TTS 与尾气排放指标仅小幅增加.方案9 偏重TTS， TTS 指标相比于均衡情况减少了1.79%，尾气排放、燃油消耗与匝道排队指标有小幅增加.方案10 偏重匝道排队， 匝道排队指标相比均衡情况小幅减少， 但是TTS、尾气排放和燃油消耗指标小幅增加.方案11 和方案12 偏重两个环境指标， 两个环境指标均得到改善， 但是匝道排队和TTS 指标均有增加.在偏重某一特定指标时， TOPSIS 偏重的性能指标可以得到改善， 且总体解符合实际情况， 可以满足决策者对于特定指标的偏好.

(4) 对比了方案13 和方案14.方案13 考虑了TTS 和TTD， 偏重主路的通行效率， TTD 指标增加了1.77%， TTS 指标减少了1.07%， 匝道排队指标和通行效率得到了提高， 但也增加了0.12%的尾气排放与1.08%的燃油消耗.方案14 考虑了尾气排放与燃油消耗指标， 偏重环境指标， 其中尾气排放指标减少了0.66%， 燃油消耗指标减少了0.41%.但是在环境指标改善的同时， 匝道排队指标增加了0.31%.总体来看， 偏重环境指标的方案可以满足决策者对于特定目标的偏好.

(5) 对比了方案15～方案18.在考虑偏重3 个目标或4 个目标的情况下， 解的选取情况基本与考虑均衡情况下得到的解一致， 即算法可以较好地处理冲突指标.因此决策者在进行有偏好决策时， 使用FNSGA-Ⅲ算法能得到满意的偏好解， 偏重环境指标或路网效率均可以得到符合实际情况的最优解.

图10 和11 分别给出了在方案3、方案5 和方案7 下， 12 条路段上小车与大车的密度热力图.

图10 方案3、方案5、方案7 下小车在不同路段的密度分布热力图Fig.10 Heat distribution maps of the density of trolleys in various sections under Scheme 3，Scheme 5， Scheme 7

(1) 由图10 可见， 方案3 偏重匝道排队指标， 在路段8～路段12 造成了密度大幅上升.对比其他方案的密度分布热力图， 在临近午高峰时造成了路段8～路段12 的拥堵.入口匝道分别在路段8 和路段10 附近， 单目标优化算法为了减少匝道的排队， 会牺牲主路的通行来保证匝道汇入， 因此造成了匝道汇入路段主路的密度激增， 引发拥堵.方案5 偏重TTD 指标， 对比其他方案， 在路段8～路段12 出现了多个密度较大的时间区段.单目标优化算法会通过提升该路段允许进入的车辆数来增加TTD.因此为了满足主路车辆数的增加， 算法尽可能多地允许匝道车辆汇入主路， 但这在实际通行中会加重主路的通行负担， 同时增加主路与匝道交汇区域的拥堵.方案7 表现最好， 对高峰时期的拥堵起到了一定的缓解作用， 使其可以较为缓和的疏散.

(2) 由图11 可见， 对比小车的密度分布， 方案3 并没有出现明显的密度激增.这是因为大车进入匝道的需求较少， 因此大车的匝道排队指标优化相比小车产生的影响较小.但在方案5 中， 对于大车TTD 指标的优化会增加大车的匝道进入量， 引发密度激增， 尤其是在早高峰时期.在其他大车方案中， 均看到有两个较为明显的密度高峰， 即早高峰与晚高峰.

图11 方案3、方案5、方案7 下大车在不同路段的密度分布热力图Fig.11 Heat distribution maps of the density of carts in various sections under Scheme 3，Scheme 5， Scheme 7

图12 和13 分别给出了在方案3、方案5 与方案7 中， 12 条路段上小车与大车的流量分布热力图.可以看到， 各方案基本具有与密度分布一样的趋势， 方案3 与方案5 有两个明显的车流高峰， 并且迟迟不能疏散.相比于方案7， 这两种方案表现较差.

图12 方案3、方案5、方案7 方案下小车在不同路段的流量分布热力图Fig.12 Heat distribution maps of the traffic flow of trolleys in various sections under Scheme 3，Scheme 5， Scheme 7

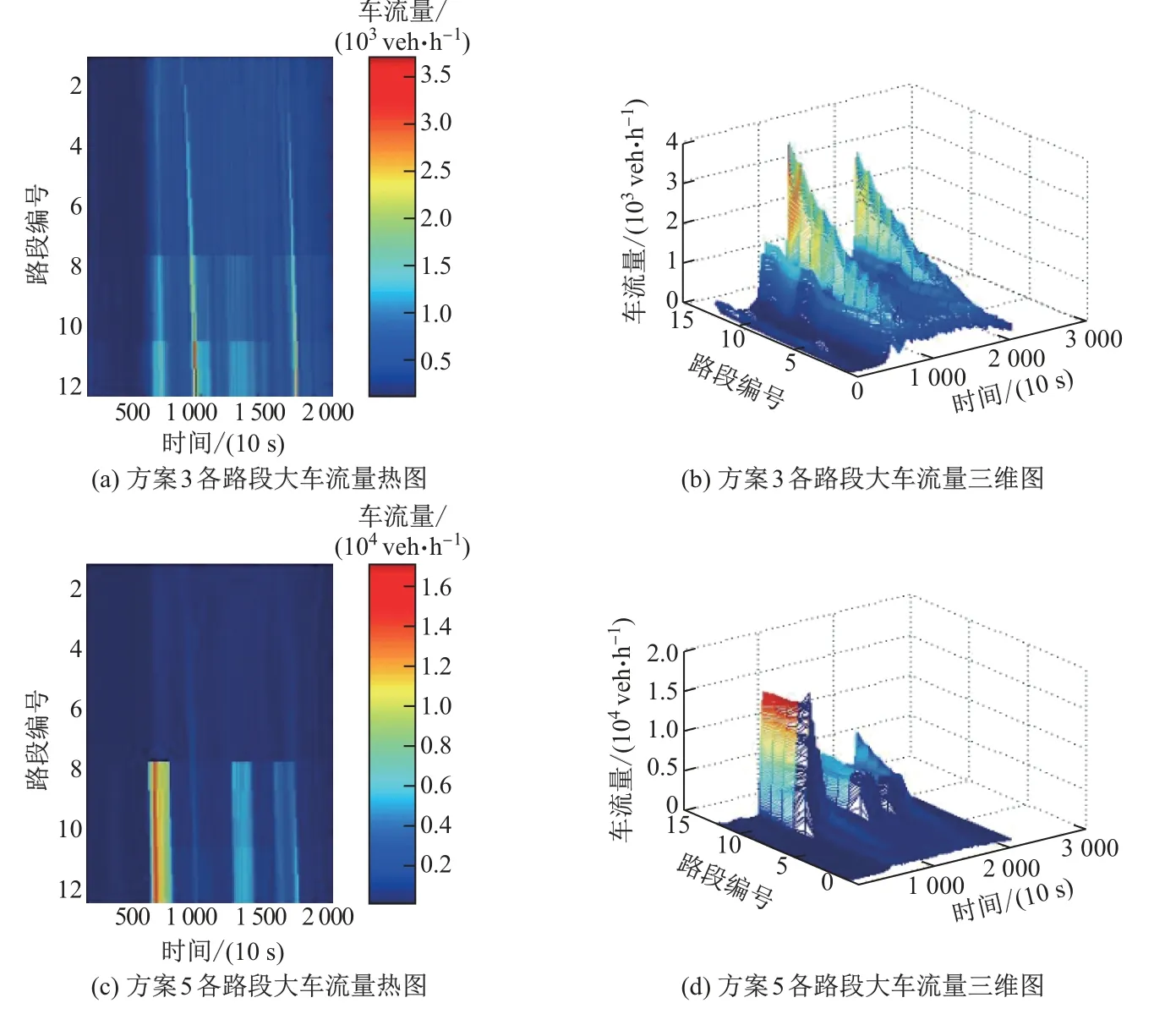
图13 方案3、方案5、方案7 方案下大车在不同路段的流量分布热力图Fig.13 Heat distribution mps of the traffic flow of carts in various sections under Scheme 3，Scheme 5， Scheme 7

4 结论与展望

本研究分析了多车型背景下城市快速路的运行过程及其特点.在考虑环境因素与道路通行效率的背景下， 结合走行时间、走行距离、匝道排队、燃油消耗与尾气排放5 个交通指标， 探究了城市快速路最优的可变限速与匝道控制策略实施方法.同时结合上海市实际道路需求， 构建了符合上海市广中路环境的Multi-class METANET 交通流模型， 设计了FNSGA-Ⅲ算法对该模型下的可变限速与匝道控制方案进行求解.在今后的研究中， 高维多目标优化算法还需要在维数较高时进化压力大、进化过程中考虑的因素不足以适应高维问题的复杂性、Pareto 超平面分布性较差等方面进行改进.此外， 现有交通流模型与实际的交通运行情况并不完全匹配， 还需从更多的角度研究影响交通状况的因素， 设计更贴近实际路网情况的交通流模型.