滨海孤石地层盾构掘进的稳定性数值分析
朱向阳,钱伟丰,朱和跃,黄明
滨海孤石地层盾构掘进的稳定性数值分析
朱向阳1,钱伟丰2,朱和跃2,黄明2
(1. 中铁十一局集团第四工程有限公司,湖北 武汉 100855;2. 福州大学 土木工程学院,福建 福州 350108)
孤石是风化岩残留体硬度高强度大,地层存在孤石是阻碍盾构施工的危害之一。依托厦门城轨交通4号线彭厝北站~蔡厝站区间,针对滨海孤石地层盾构掘进的稳定性进行离散元数值分析,分别研究孤石与隧道距离、隧道埋深、孤石位置及盾尾空隙对地层稳定性的影响。研究结果表明:随着孤石与隧道距离增大,地层扰动范围、拱顶衬砌压力变化及地表沉降都有减小的趋势;随着隧道埋深的增大,地层扰动范围及地表沉降都呈减小趋势,衬砌土压力整体上呈现增大趋势;随着孤石位置逐步远离隧道顶部,地层扰动范围及地表沉降都呈减小趋势,孤石位于拱肩、拱脚、仰拱底时衬砌压力产生突变;随着盾尾空隙增大地层扰动程度及地表沉降也增大,衬砌拱顶土压力呈增大趋势。
孤石;盾构隧道;数值模拟;稳定性分析
孤石又称为球状风化体,具有分布随机、大小不一、强度大等特点,是地铁盾构施工中较难处理的问题之一[1]。孤石会给隧道施工带来极大风险,诸如刀盘刀具磨损严重、造成地层空洞及引起掘进方向偏离等[2]。盾构推进过程中由于盾尾空隙、线路弯度、人为操作等问题致使地层的扰动不可避免,上述扰动往往通过地表沉降、地层位移、地层应力等方面得到体现,摸清含孤石地层导致盾构推进地层扰动的内在机理,有利于科学合理地采取相关措施控制盾构推进过程中对地层的扰动。目前,关于孤石地层中隧道掘进的研究主要针对工程技术和孤石勘探方面。王鹏华等[3-4]结合土压平衡盾构施工的工程实例,介绍了孤石破除方法,并针对困难地层提出一些处置措施及注意事项。章飞亮等[5]采用微动技术对南方某城市地铁隧道区间的孤石进行探测,该方法能够较为准确的探测到孤石分布状况。李术才等[6]采用跨孔电阻率CT法对广州地铁某站点进行孤石的分布物探,明确探测出孤石位置。Sarracino等[7]建立了孤石与地层关系的数学模型,并给出了孤石的形成过程和对周边地层的影响。陈万垒等[2]利用离限元模型软件,分析孤石及基岩突起对盾构工程引起的地表塌陷的机理。以上研究均侧重于施工技术,对于含孤石地层稳定性的探讨少之又少。国内外学者关于隧道掘进过程中地层稳定性的研究较多。Atkinson等[8−9]得到了相应的沉降槽经验曲线公式。Peck[10]基于统计总结盾构隧道开挖的地表沉降情况,提出了预测地表沉降的方法。何川等[11]基于砂卵石地层盾构推进对邻近桩基、邻近既有隧道的扰动影响进行了模型试验研究,多角度分析了扰动的特点。Lee等[12]采用多种方法基于隧道开挖过程对地层的变形及应力进行了分析。邱明明等[13]基于某城市地铁盾构隧道运用有限差分软件FLAC3D对盾构推进引起的地层变形进行了分析。但是对隧道穿越孤石地层引发的地层稳定性的研究较少。因此,本文依托厦门市城市轨道交通4号线彭厝北站~蔡厝站区间,借助PFC2D离散元数值模拟软件,开展滨海孤石地层盾构掘进的稳定性数值分析。
1 工程概况
我国东南沿海城市已建和在建的地铁部分盾构区间工程穿越地层地质复杂,其中孤石地层是盾构施工的最大难题之一,盾构在穿越孤石地层时容易出现刀片磨损严重与地层扰动较大等问题。而福建省花岗岩地质面积约占全省的1/3,该地区孤石的形成主要在花岗岩地层中,且以化学风化作用为主。
本文依托厦门市城市轨道交通4号线彭厝北站~蔡厝站区间,场区地表大面积分布有杂填土、素填土、吹填淤泥及吹填砂地层;场区分布的软土主要有吹填淤泥、淤泥地层;场区分布的残积土及风化岩风化状态均匀性差,且还具有软化性、崩解性及抗扰动性较差等特点,且基岩风化岩中存在风化不均匀体(即孤石),对盾构正常推进具有较大的影响。由于项目施工现场需要保证盾构的安全推进,较难获得掌子面失稳时的破坏形态,加之在孤石与全风化花岗岩地层分析中涉及到接触问题处理的复杂性,因此综合数值分析的实际要求及计算效率选择离散元软件PFC2D,并分别计算分析各因素变化下隧道顶部扰动程度较大的范围、隧道衬砌土压力及隧道上部地表沉降的变化趋势。基于上述3种因变量的变化规律,从盾构隧道规划、设计及施工的角度初步提出相应的孤石处置措施。
2 孤石地层数值模型的构建
2.1 几何模型
采用PFC2D软件建立离散元盾构隧道模型,模型尺寸为80 m×31 m的矩形,且模型关于盾构隧道左右对称,盾构隧道直径=6 m,模型地表面为自由,其余四周采用变形约束条件,衬砌管片采用wall单元模拟,模型如图1所示。分别取以下几种孤石存在状态为单一变量因素,即孤石与隧道的距离、隧道埋深、孤石位置、盾尾空隙。孤石与隧道的距离指孤石底部边界与隧道拱顶处边界之间的距离,用表示。隧道埋深指隧道拱顶至地表的距离,用表示。盾尾空隙是由于盾构掘进过程中对地层的扰动以及盾构掘进超挖和注浆不及时等原因共同作用形成,盾尾空隙如图2所示,用表示。
2.2 计算参数选取
针对全风化花岗岩地层及孤石的力学特征,本文采用孙锋[14]通过二维离散元单轴试验所获得的颗粒参数取值,如表1及表2所示。此外,全风化花岗岩地层与微风化花岗岩孤石之间的接触参数通过PFC2D中自带的属性继承功能而获得。

单位:m

图2 隧道盾尾空隙示意图
3 孤石对盾构隧道地层稳定性的影响
3.1 孤石与隧道间距变化对地层稳定性的影响
为了分析孤石与隧道之间不同距离条件下,隧道围岩竖向及矢量位移、衬砌压力及地表沉降的变化趋势。根据控制单一变量因素原则,取隧道埋深=15 m(2.5),盾尾空隙=30 cm,分别进行无孤石(工况1),=0.5 m(工况2),=1.0 m(工况3),=2.5 m(工况4),=4.0 m(工况5),=5.5 m(工况6)及=7.0(工况7),为分析孤石对不同工况下的计算结果的影响,选取无孤石地层作为空白对照组,不同距离条件下地层位移矢量及竖向位移如图3所示。
由图3可得,开挖卸载作用下,各工况盾构隧道底部均出现一定的隆起现象。然而7组工况盾构隧道上部地层竖向位移出现左移的现象,即盾构隧道上部轴线左侧竖向沉降略大于右侧,当孤石存在时左移现象越为明显。出现这种现象的原因在于PFC2D属于颗粒流离散元计算软件,对于类似工况地层重复性数值计算需设置随机种子数,而随机种子作为模型颗粒生成的随机规律分布特征的保障,可满足每次计算模型生成颗粒的初始分布位置及半径不发生变化。由于本次数值模型颗粒生成随机种子数均为相同定值,加之孤石的存在对地层整体均匀性的影响,因此含孤石地层竖向位移出现整体性左右略微不对称的情况。

表1 岩体物理力学参数

表2 颗粒基本参数
以扰动范围边界距隧道顶部的距离为界限对盾构隧道围岩扰动程度的区域进行划分,如表3所示,不同距离条件下衬砌土压力如图4所示,不同距离条件下地表沉降曲线如图5所示。

(a) 无孤石;(b) d=0.5 m;(c) d=1.0 m;(d) d=2.5 m;(e) d=4.0 m;(f) d=5.5 m;(g) d=7.0 m

单位:kPa

表3 不同距离条件下扰动范围边界距隧道顶部距离
由表3可见,无孤石地层条件下,其扰动程度较大范围最小,表明由于孤石作用加大了盾构推进对地层的扰动程度及范围,因此在含孤石地层的注浆加固范围应比一般地层有所扩大。随着距离的增大,孤石地层的扰动程度逐渐减小且趋于稳定。
由图4可得,盾构隧道衬砌管片所受土压力基本呈仰拱底、拱顶(拱腰)、拱脚(拱肩)的下降趋势,由于盾构掘进过程中对地层的扰动效应及不可避免的盾构间隙影响,加之隧道围岩土层向隧道正上部不均匀沉降的趋势,隧道上部一定地层范围出现近似锥形的沉降槽,由此分析得出的拱腰处土压力值较传统计算方法,即垂直土压力乘以侧压力系数得出的结果偏大,其更符合实际情况。
由图5可得,孤石的形成是由于地层的长期风化作用,孤石与其四周较近地层形成一定的整体固结性,加之孤石基本在5,6和24号衬砌正上方,距离为0.5 m,1.0 m的含孤石地层盾构隧道拱顶衬砌土压力分布较为均衡;如上文所述含孤石地层隧道上部竖向位移左侧略大于右侧,因此,地层自承压力衬砌点也出现向左移动的情况,即距离4.0,5.5及7.0 m的含孤石地层6号衬砌出现压力增大的情况。
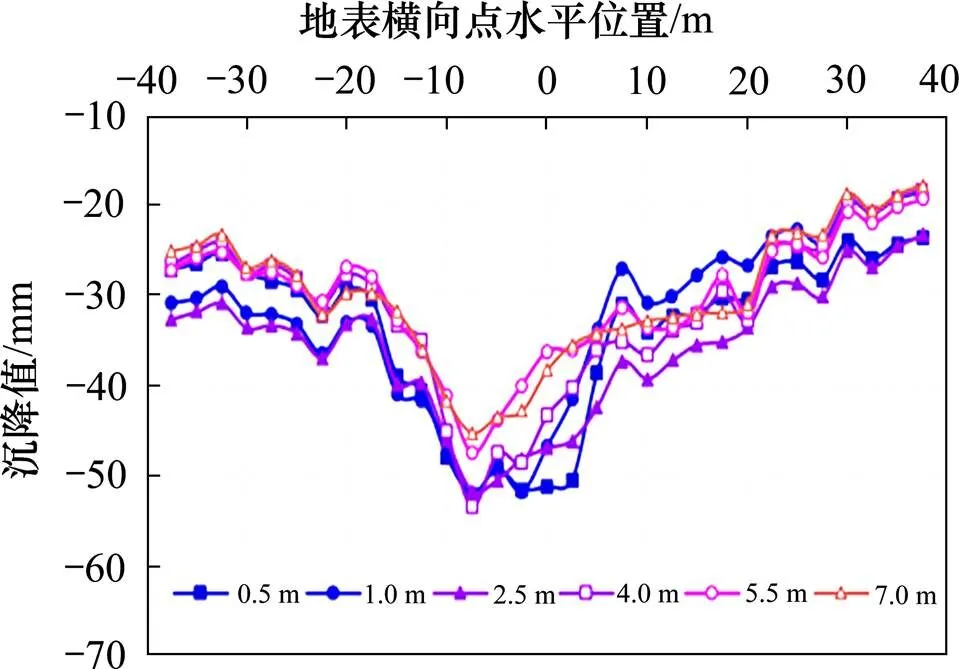
单位:mm
各工况地表沉降在部分位置处均表现出一定的离散特性,但总体上符合Peck沉降曲线形式。7组工况中距离为0.5,1.0及2.5 m的含孤石地层,其地表沉降较为接近,随着孤石与隧道距离的依次增大,地表沉降相应呈减小趋势。
3.2 隧道埋深变化对盾构隧道地层稳定性的影响
为了分析含孤石地层不同盾构隧道埋深条件下隧道围岩竖向及矢量位移、衬砌压力及地表沉降的变化趋势,取其他影响因素值为固定值,即孤石与隧道之间距离=1.0 m,盾尾空隙=30 cm,孤石位于拱顶正上部。隧道埋深分别取=6 m(1),=12 m(2),=15 m(2.5),=18 m(3)和=24 m(4)进行计算。不同盾构隧道埋深条件下地层位移矢量及竖向位移图如图6所示,不同埋深条件下扰动范围边界距隧道顶部距离如表4所示,不同埋深条件下衬砌土压力图如图7所示,不同埋深条件下地表沉降曲线如图8所示。
由图6可知,随着盾构隧道埋深的逐步增大,隧道上部浅层区域的位移逐步减小,即符合上文所述的盾构掘进对地层扰动随地层距隧道距离的增大而衰弱的特点。埋深为6 m的隧道由于埋深较浅致使土层破坏贯穿至地表,属于塌穿型塌方,其他5组工况均属于拱形塌方。
由表4可见,不同埋深的含孤石地层,其较大扰动范围边界呈现从隧道埋深为2至4依次增大且逐渐稳定的趋势。盾构施工对地层扰动随隧道埋深的增大而减小,对于含孤石地层盾构施工可根据隧道埋深情况酌情考虑对孤石是否采取处置 措施。

表4 不同埋深条件下扰动范围边界距隧道顶部距离
由图7可知,隧道拱顶土压力分布趋势随埋深的增大而增大的趋势,与其含孤石地层扰动较大程度范围分布趋势一致,其次埋深2,2.5,3及44组工况中,由于地层的压力拱自承作用,虽然其拱顶土压力基本呈随埋深的增大而增大的趋势,但变化幅度较为微小,加之除拱顶外隧道衬砌其他部位基本呈随隧道埋深增大而增大,且增大幅度较为明显,由此表明上述4组工况均形成了较为明显的压力拱自承效应。

(a) 埋深1D竖向位移及矢量图;(b) 埋深2D竖向位移及矢量图;(c) 埋深2.5D竖向位移及矢量图;(d) 埋深3D竖向位移及矢量图;(e) 埋深4D竖向位移及矢量图
单位:kPa

单位:mm
由图8可知,埋深为1的盾构隧道未形成压力拱,其上部地层破坏位移直接贯穿至地表,最大沉降达至143 mm,其余4组工况均形成明显的压力拱现象,地表沉降较为接近。随着隧道埋深的增大,其对地表的扰动呈现减小的趋势,由此说明虽然孤石对盾构掘进一定程度上会加大对地层的扰动效果,但地层的压力拱自承作用对减小地表沉降具有较好的效果。
3.3 孤石位置变化对盾构隧道地层稳定性的影响
为了分析不同孤石与隧道相对位置条件下隧道围岩竖向及矢量位移、衬砌压力及地表沉降的变化趋势,取其他影响因素值为固定值。孤石与隧道相对位置分别取孤石位于隧道的仰拱底、拱脚、拱腰、拱肩及拱顶处进行计算。不同孤石位置条件下地层位移矢量及竖向位移图如图9所示,不同孤石位置下扰动范围边界距隧道顶部距离如表5所示,不同孤石位置条件下衬砌土压力图如图10所示,不同孤石位置条件下地表的沉降曲线如图11所示。

(a) 孤石位于隧道拱顶处;(b) 孤石位于隧道拱肩处;(c) 孤石位于隧道拱腰处;(d) 孤石位于隧道拱脚处;(e) 孤石位于隧道仰拱底处
由图9可知,除孤石位于隧道拱脚处的工况外,其他几组工况均出现在隧道上部轴线处,无孤石一侧的地层竖向位移及矢量位移大于有孤石一侧的现象。出现这种现象的原因是,压力拱效应导致盾构隧道上部的土体颗粒在开挖后向两侧移动,由于本次数值模型土体颗粒生成随机种子数均为相同定值,而模型中孤石的存在阻碍了土体颗粒的移动,因此导致了这种现象的产生,特别是当孤石位于盾构隧道的拱肩、拱腰、拱脚处时,无孤石一侧的地层竖向及矢量位移大于有孤石一侧的现象愈发明显。

表5 不同孤石位置下扰动范围边界距隧道顶部距离
由表5可见,孤石位于隧道拱顶处对地层的扰动范围最大,说明拱顶处孤石随盾构推进而发生较大转动及沉降,继而加大了盾构推进对地层的扰动影响程度;随着孤石位置逐步远离隧道顶部,其对地层的扰动较大程度范围逐步减小,说明在含孤石地层盾构施工时应重视孤石位于隧道上部对地层扰动程度。
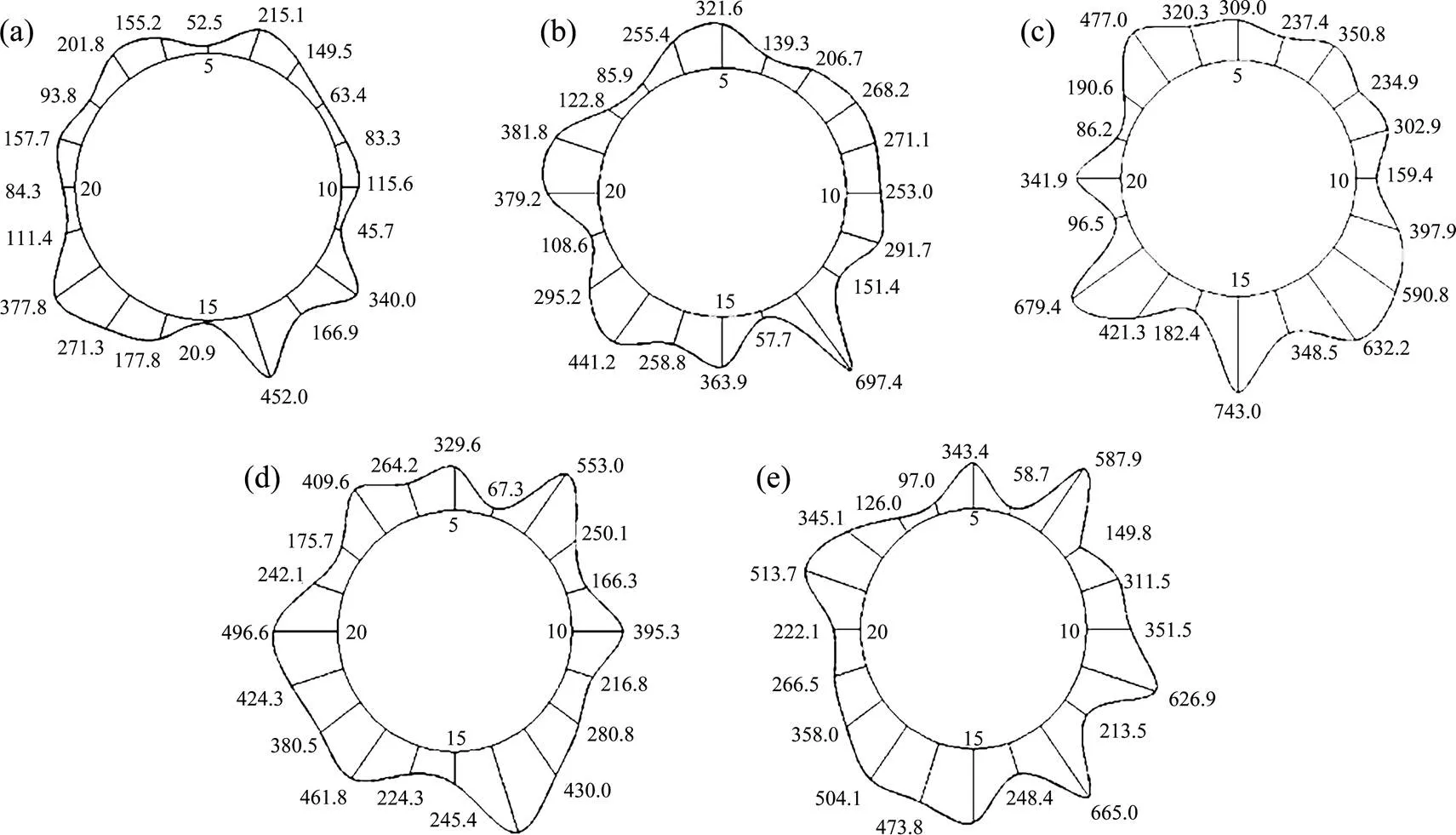
由图10可得,孤石位于拱肩位置处时隧道拱肩处衬砌压力445.6 kPa(即7号衬砌),为所有工况中拱肩处衬砌压力最大值,且最大压力旁边又出现了最小压力5.5 kPa(即8号衬砌),此处出现了一定程度的衬砌压力突变。高峰等[15]认为,隧道开挖后,边墙附近的围岩颗粒的接触力全部升高,在拱顶和仰拱底附近区域的围岩压力环的环间接触力降低,降低的接触力连线基本上呈现抛物线形。
因此出现上述现象的原因可能是孤石正好位于降低的接触力连线的边界上,由于孤石在此处产生应力集中导致了衬砌压力突变。孤石位于隧道拱腰处时,由于拱腰处孤石与隧道衬砌处平行,孤石重力并未直接作用在衬砌上,未发生衬砌压力比其他工况明显增大的现象。孤石位于隧道拱脚处时也出现了衬砌压力突变,拱脚处衬砌土压力为79.5,564.7和618.8 kPa(即12,13和14号衬砌)。孤石位于仰拱底位置处时同样也出现了衬砌压力突变,仰拱底处衬砌土压力为675.4 kPa,13.6 kPa(即15,16号衬砌),出现这种现象的原因均与孤石位于隧道拱脚处时的相同。

单位:kPa

单位:mm
由图11可得,各工况地表沉降均表现出一定的Peck沉降曲线形式,各工况的最大沉降点发生在隧道中心点略偏左侧地表处。各工况地表沉降呈现随孤石位置远离隧道顶部而降低的趋势,孤石位于隧道拱顶及拱肩处时地表沉降较为接近,孤石位于隧道拱脚及仰拱底时地表沉降较为接近,说明孤石位于拱顶、拱肩及拱脚、仰拱底2组工况由于孤石位置较为靠近致使其对盾构隧道掘进地层的扰动具有同一量级影响程度,其次,孤石位置距隧道顶部越远,其对盾构推进地层的扰动程度降低较为明显。
3.4 盾尾空隙变化对盾构隧道地层稳定性的影响
为了分析不同盾尾空隙条件下隧道围岩竖向及矢量位移、衬砌压力及地表沉降的变化趋势,取其他影响因素值为固定值,孤石与隧道距离=1.0 m,隧道埋深=15 m(2.5),孤石位于拱顶正上部,盾尾空隙分别取值=5,=15,=20,=30和=40 cm进行计算。不同盾尾空隙下地层位移矢量及竖向位移图如图12所示,不同盾尾空隙下扰动范围边界距隧道顶部距离如表6所示,不同盾尾空隙下衬砌土压力图如图13所示,不同盾尾空隙下地表沉降曲线如图14所示。

(a) 盾尾空隙5 cm;(b) 盾尾空隙15 cm;(c) 盾尾空隙20 cm;(d) 盾尾空隙30 cm;(e) 盾尾空隙40 cm
由图12可得,在盾尾空隙形成后,应力开始释放,空隙周围土体颗粒向下移动,土体颗粒在运动的过程中相互接触力很小,而且颗粒接触力链较周围稀疏,此时土体发生应力松弛。随着盾尾空隙的增大,空隙周围的土体颗粒逐渐向空隙处塌落,拱顶处由于空隙最大,颗粒坍塌的发展较衬砌两边迅速,同时沉降和影响范围也最大。最后衬砌两边的颗粒运动逐渐停止,而此时拱顶上方的土体颗粒运动并没有停止,而是进一步向地表延伸。
由表6可见,地层扰动程度范围随盾尾空隙增大而增大,其中盾尾空隙为5,15及20 cm工况的扰动程度范围较为接近,且盾尾空隙为5 cm和15 cm 2组工况距地表较近的浅层区域竖向及矢量位移明显较其他工况偏小,表明较小盾尾空隙下孤石地层的扰动程度较小且稳定,但随着盾尾空隙逐步增大至30 cm和40 cm时,其对地层的扰动程度范围增大较为明显。

表6 不同盾尾空隙下扰动范围边界距隧道顶部距离

单位:kPa
由图13可得,上述5组工况拱顶土压力大小分布趋势与上节扰动较大程度范围分布趋势一致,即随盾尾空隙的逐步增大拱顶土压力呈逐步增大的趋势;其次,各工况隧道拱侧、拱脚及仰拱底的衬砌土压力分布较为接近,表明位于隧道上部孤石对隧道下半部分地层扰动影响的有限性。
由图14可得,各工况地表沉降均表现出一定的Peck沉降曲线形式,各工况的最大沉降点基本发生在隧道中心略偏左侧地表处。随着盾尾空隙的增大地表沉降整体上呈现增大的趋势,盾尾空隙越大地表沉降增大的程度越大。考虑到隧道盾尾空隙一定程度上反映着盾构推进对地层的扰动情况,地层扰动随盾尾空隙增大而具有增大的趋势,因此在含孤石地层盾构掘进的过程中,通过合理的控制盾尾注浆及调整盾构掘进参数对盾构施工具有十分重要的意义。

单位:mm
4 结论
1) 随着孤石与隧道距离的依次增大,地层的扰动程度、拱顶衬砌压力的变化趋势及地表沉降都具有减小的趋势。同时出现盾构隧道上部轴线左侧竖向位移略大于右侧的现象,是由于离散元模型颗粒生成随机种子数均为相同定值,加之孤石的存在对地层整体均匀性的影响,因此含孤石地层竖向位移出现整体性左右略微不对称的情况。
2) 不同埋深含孤石地层较大扰动范围边界呈现从隧道埋深为2至4依次增大且逐渐稳定的趋势,由于地层的压力拱自承作用,虽然其拱顶土压力随埋深的增大而增大,但变化幅度较为微小。埋深为1的盾构隧道未形成压力拱,其上部地层破坏位移直接贯穿至地表;随着埋深的增大,地层的压力拱自承作用对减小地表沉降具有较好的 效果。
3) 由于盾构隧道开挖产生了压力拱效应,隧道上部的土体颗粒在开挖后向两侧移动,而模型中孤石的存在阻碍了土体颗粒的移动,所以导致了除孤石位于隧道拱脚处的工况外,其他几组工况均出现在隧道上部轴线处,无孤石一侧的地层竖向位移及矢量位移大于有孤石一侧的现象。孤石位于隧道拱顶处对地层扰动程度范围为最大值,随着孤石位置逐步远离隧道顶部,其对地层的扰动程度范围逐步减小,相应的地表沉降表现出类似的变化趋势。孤石位于拱肩、拱脚、仰拱底位置处时出现衬砌压力突变,这是由于孤石正好位于降低的接触力连线的边界上,由于孤石在此处产生应力集中导致了衬砌压力突变。
4) 随着盾尾空隙增大地层扰动程度也增大,较小盾尾空隙下扰动程度较小且稳定,随盾尾空隙的增大地表沉降也逐渐增大,且盾尾空隙越大其地表沉降增大的程度越明显;同时各工况隧道拱侧、拱脚及仰拱底的衬砌土压力分布较为接近,拱顶土压力呈逐步增大的趋势,表明位于隧道上部孤石对隧道下半部分地层扰动影响的有限性。考虑到隧道盾尾空隙一定程度上反映了盾构推进对地层的扰动情况,因此在盾构施工过程中应通过盾尾注浆及调整掘进参数等方法对盾尾空隙进行控制。
[1] 刘建国. 深圳地铁盾构隧道施工技术研究与实践[M]. 北京: 人民交通出版社, 2011. LIU Jianguo. Research and practice of construction technology of Shenzhen Metro shield tunnel[M]. Beijing: China Communications Press, 2011.
[2] 陈万垒, 谭勇, 李想, 等. 盾构掘进破坏孤石诱发地层塌陷的灾变机制研究[J]. 隧道建设(中英文), 2018, 38(5): 824−832. CHEN Wanlei, TAN Yong, LI Xiang, et al. Study of mechanism of ground subsidence induced by boulder breaking during shield tunneling[J]. Tunnel Construction, 2018, 38(5): 824−832.
[3] 王鹏华. 不同地质条件下盾构工程孤石处理工艺及实例[J]. 隧道建设, 2012, 32(4): 571−575. WANG Penghua. Treatment of boulders encountered in shield tunneling under different geological conditions[J]. Tunnel Construction, 2012, 32(4): 571−575.
[4] 黄恒儒. 盾构穿越花岗岩球状风化孤石群的施工关键技术[J]. 隧道建设, 2015, 35(8): 834−840. HUANG Hengru. Key technologies for shield boring through ground containing weathered spherical granite boulder groups[J]. Tunnel Construction, 2015, 35(8): 834−840.
[5] 章飞亮, 闫高翔, 袁真秀, 等. 微动技术在地铁隧道区间孤石探测中的应用. 工程地球物理学报, 2015, 17(6): 817−822. ZHANG Feiliang, YAN Gaoxiang, YUAN Zhenxiu, et al. The application of micro technology to boulders detection in subway tunnel[J]. Chinese Journal of Engineering Geophysics, 2015(6): 817−822.
[6] 李术才, 刘征宇, 刘斌, 等. 基于跨孔电阻率CT的地铁盾构区间孤石探测方法及物理模型试验研究[J]. 岩土工程学报, 2015, 37(3): 446−457. LI Shucai, LIU Zhengyu, LIU Bin, et al. Boulder detection method for metro shield zones based on cross-hole resistivity tomography and its physical model tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(3): 446−457.
[7] Sarracino R S, Prasad G. A mathematical model of spheroidal weathering[J]. Mathematical Geology, 1987, 19(4): 269−289.
[8] Atkinson J H, Potts D M. Subsidebce above shallow tunnels in soft ground[J]. ASCE J Geotech Eng Div, 1977, 103(4): 307−325.
[9] Yoshikoshi W. Osamu W. Takagaki N. Prediction of ground settlements associated with shield tunneling[J]. Soils and Foundations, 1978, 18(4): 47−59.
[10] Peck. Deep excavations and tunneling in soft ground[C]// 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico, 1969: 225−290.
[11] 何川, 汪洋, 方勇, 等. 土压平衡式盾构掘进过程的相似模型试验[J]. 土木工程学报, 2012, 45(2): 162−169. HE Chuan, WANG Yang, FANG Yong, et al. Similarity model test of earth-pressure-balanced shield tunneling process[J]. China Civil Engineering Journal, 2012, 45(2): 162−169.
[12] Lee K M, Rowe R K. An analysis of three-dimensional ground movements: The Thunder Bay Tunnel[J]. Canadian Geotechnial Journal, 1991, 28(1): 25−41.
[13] 邱明明, 杨果林, 姜安龙, 等. 地铁盾构施工地层变形预测及数值分析[J]. 深圳大学学报(理工版), 2016, 33(4): 377−387. QIU Mingming, YANG Guolin, JIANG Anlong, et al. Numerical analysis of stratum deformation induced by tunnel boring machine construction for metro[J]. Journal of Shenzhen University (Science and Engineering), 2016, 33(4): 377−387.
[14] 孙锋. 海底隧道风化槽复合注浆堵水关键技术研究[D]. 北京: 北京交通大学, 2010. SUN Feng. Study on the key technique of composit grouting for water blockage in weathered slot of subsea tunnel[D]. Beijing: Beijing Jiaotong University, 2010.
[15] 高峰, 谭绪凯, 陈晓宇, 等. 基于离散−连续耦合方法的隧道压力拱特性研究[J]. 计算力学学报, 2020, 37(2): 218−225. GAO Feng, TAN Xukai, CHEN Xiaoyu, et al. Research on tunnel pressure arch based on coupled discrete and continuous method[J]. Chinese Journal of Computational Mechanics, 2020, 37(2): 218−225.
[16] 胡雄玉. 土压平衡式盾构掘进对砂土地层的扰动研究[D]. 成都: 西南交通大学, 2013. HU Xiongyu. Study on ground disturbance in sandy stratum using earth pressure balance (EPB) shield[D]. Chengdu: Southwest Jiaotong University, 2013.
Numerical analysis of the stability of shield tunneling in the coastal isolated rock stratum
ZHU Xiangyang1, QIAN Weifeng2, ZHU Heyue2, HUANG Ming2
(1. China Railway 11th Bureau Group Fourth Engineering Co., Ltd., Wuhan 100855, China;2. College of Civil Engineering, Fuzhou University, Fuzhou 350108, China)
Boulder is a kind of weathered rock residue with high hardness and strength, which is one of the most harmful problems to shield machine. Based on the interval between Pengcuo north station and Caicuo station of Xiamen rail transit line 4, this paper analyzed the stability of shield tunneling in the coastal boulder stratum by discrete element method, and studied the influence of the distance between the boulder and the tunnel, the buried depth of the tunnel, the location of the boulder and the gap between the shield tail on the stability of the stratum. The results show that with the increase of the distance between the boulder and the tunnel, the disturbance range of the stratum, the change of the lining pressure of the arch crown and the settlement of the earth’s surface all decrease. With the increase of the depth of the tunnel, the disturbance range of the stratum and the settlement of the ground decrease, and the earth pressure of the lining increases as a whole. With the location of the boulder gradually away from the top of the tunnel, the disturbance range of the stratum and the settlement of the earth’s surface are decreasing. With the increase of the gap at the tail of shield and the increase of the ground settlement, the earth pressure on the lining vault increases.
boulders; shield tunnel; numerical simulation; stability analysis

U455.43
A
1672 − 7029(2021)01 − 0172 − 12
10.19713/j.cnki.43−1423/u.T20200276
2020−04−06
国家自然科学基金资助项目(41672290);中铁十一局集团公司A类重点研发计划项目(2018121104)
朱向阳(1977−),男,湖北武汉人,高级工程师,从事城市地铁等领域的施工技术研究工作;E−mail:455233268@qq.com
(编辑 阳丽霞)

