高速磁浮单线隧道车体压力载荷特征
张志超,杜健,赵汗冰,梅元贵
高速磁浮单线隧道车体压力载荷特征
张志超1,杜健2,赵汗冰1,梅元贵1
(1. 兰州交通大学 甘肃省轨道交通力学应用工程实验室,甘肃 兰州 730070;2. 中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
高速磁浮列车通过隧道过程中将引起剧烈的压力波动,造成司乘人员耳感舒适性、车体及其零部件、隧道衬砌及辅助设施的气动疲劳寿命问题,有必要对磁浮列车高速通过隧道时压力波效应进行研究。采用一维可压缩非定常不等熵流动模型和广义黎曼变量特征线法对单列车通过隧道时车体压力载荷进行数值模拟研究,初步揭示隧道长度、列车速度、阻塞比对车外压力波的影响规律;得出时速500~600 km/h速度下基于最大正负值和最大压力峰峰值的最不利隧道长度;论证了列车通过隧道产生的压力波幅值与列车速度平方成正比的适用范围,总结了压力最值与速度的拟合关系式。本文研究方法和结果可为车体设计选用气动载荷提供参考依据。
高速磁浮列车;隧道;压力波;车体气动载荷;一维流动模型特征线法
近20年来,国外磁悬浮技术应用于现代交通,并成为高科技的现代地面交通运输方式,已取得突破性进展,进入到了商业性的综合技术运行。德国的常导高速磁浮列车和日本的超导高速磁浮列车,都以超过500 km/h的试验速度向世人展示了磁浮列车技术的成熟[1]。目前,我国正在积极大力研究时速600 km高速磁浮交通关键技术,时速600 km高速磁浮试验样车在青岛已下线[2]。与轮轨高速一样,空气动力学问题也是磁浮交通研发过程中的关键技术之一。随着列车运行速度的不断提高,其空气动力学问题将会越来越显著。一般而言,列车通过隧道诱发的压力波变化幅值与列车运行速度的平方成正比[3],剧烈的压力波动会造成司乘人员耳感舒适性、列车车体及其零部件、隧道衬砌及洞内辅助设施的气动疲劳寿命等一系列问题[4−5]。就高速磁浮列车空气动力学问题而言,研究方法主要包括实车试验、风洞试验、数值模拟。以德国的常导高速磁浮列车为研究对象,Ravn等[6]采用基于一维可压缩流动模型特征线数值方法的Thermotun软件,重点研究了慕尼黑最高时速350 km的机场磁浮线可行方案中隧道压力波效应等问题;Howell[7]采用动模型试验方法研究了横风对磁浮列车的影响特性;Tielkes[8]较为系统分析得出对德国磁浮交通系统隧道空气动力学问题中也应重点关注列车及隧道方面的气动载荷和气动阻力;自1997年日本山梨试验线投入使用以来,进行了多次全尺寸实车试验[9],得到了包含空气动力学在内大量的磁浮列车试验数据,为今后对于磁浮列车在空气动力学方面的研究提供了数据支撑;针对磁浮列车高速运行带来的司乘人员舒适性、气动载荷、隧道净空面积选取等一系列问题,日本学者在头型优化、车内压力保护技术、隧道洞口微气压波的缓冲结构方面采用数值模拟方法做了大量的研究[10−12];考虑到更高速度下列车通过隧道特点,Saito等发展了一维可压缩非定常不等熵流动模型特征线法模拟隧道压力波的计算方法和源代码程序,并通过了500 km/h旋成体动模型试验结果的验证,提高了原有日本轮轨高速隧道压力波常用的定密度有限声速一维非定常流动特征线法的计算精度[13, 23],为日本研究超高速轨道交通隧道压力波问题提供了有效工具。国内对高速磁浮交通空气动力学问题的系统性深入研究,主要是以引进德国TR08磁浮交通技术为契机开始的。刘堂红等[14]对不同外形磁浮列车的气动性能进行了比较;李颢豪等[15]采用三维数值模拟方法研究了磁浮列车在不同的声屏障内交会时,列车、声屏障及电缆的气动效应。黄尊地 等[16]对真空管道交通列车气动阻力进行数值模拟,研究成果为克努森数特征长度的取值、真空管道内流体流动状态的判断、真空空气动力学数值计算的开展提供理论依据。近期,HUANG等[17−18]采用CFD软件研究了时速400 km磁浮列车在交会过程中压力波及效应问题、以及列车编组长度对车外边界层和尾流的影响规律。王国静等[19]采用有限元分析软件对160 km/h新型中速磁浮交通列车的车体强度进行分析。围绕磁浮列车隧道压力波问题,王兆祺 等[20]从空气动力学基本原理出发,推导了按非恒定流计算磁悬浮列车在驶入、通过和驶出隧道3种不同工况下空气阻力的表达式,张光鹏等[21]采用一维可压缩非定常不等熵流动模型特征线法研究了气密性对车内压力和乘客舒适性的影响特征,提出了时速200~400 km隧道净空面积建议值。综上所述,国内外对磁浮列车空气动力学问题的研究主要采用实车试验、风洞试验、CFD数值模拟来研究列车通过隧道时气动阻力、流场分布、交会压力波、隧道净空面积、横向振动、列车风等方面的问题,对于磁浮列车高速通过中长、特长隧道时车体压力载荷问题并未做深入研究,目前还未见到公开发表的报道。本文以我国高速磁浮列车为研究对象,在与日本时速500 km动模型试验结果验证基础上,利用一维可压缩非定常不等熵流动模型研究单列车通过隧道时压力波变化特征。研究了列车速度、隧道长度和阻塞比对压力波的影响特性,得出在时速500~600 km/h速度下基于最大正负值和最大压力峰峰值的最不利隧道长度,论证了列车通过隧道产生的压力波变化幅值与列车速度平方成正比的适用范围,总结了压力最值与速度的拟合关系式,并根据国内近期颁布的磁浮铁路技术标准[22]建议的隧道净空面积,得出了阻塞比的影响规律。本文研究结果可为磁浮列车车体强度设计提供数据参考。
1 隧道压力波计算模型
磁浮列车在隧道内运行时引起的空气流动是三维可压缩非定常紊流流动;当隧道长度远大于隧道的水力直径时,同一截面上的流动可认为是均匀的,即同一截面上的压强近似相等。根据上述假定,磁浮列车通过隧道时产生的压力波动问题,可采用一维、可压缩、非定常流动模型来处理。根据连续性、动量、能量方程建立隧道内一维可压缩非定常不等熵流动模型控制方程[23]。
连续性方程:

动量方程:
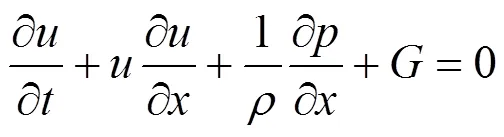
能量方程:
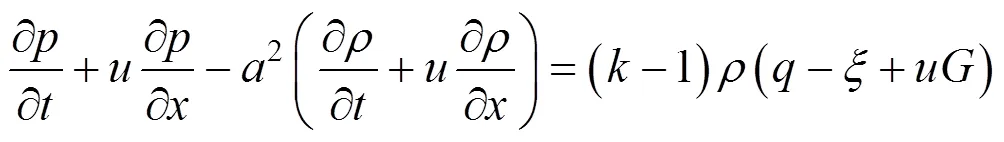
式中:,,,,,和分别为气体压力、空气流速、空气密度、当地声速、气体比热比、传热项和摩擦项。
上述隧道内一维可压缩非定常不等熵流动控制方程组为一阶拟线性双曲型偏微分方程组,可采用特征线方法求解[23],本文在此不做赘述。
2 方法验证
采用日本旋成体动模型试验来验证本文上述计算方法在更高速度条件下数值模拟的精度和合理性[13]。其中,旋成体列车与隧道模型,试验列车采用椭圆旋成体模型(长细比=3),车长1 300 mm,列车直径34.6 mm,鼻长51.9 mm,隧道为圆管式结构,隧道长14 700 mm,直径100 mm,横截面积为7 850 mm2。模型的缩尺比为1/97,车速为500 km/h。
在日本旋成体动模型试验中,压力测点布置在距隧道入口端2.35 m处的隧道壁面上。图1表示一维程序计算结果与日本旋成体动模型试验数据对比,本文一维程序计算结果和动模型试验数据吻合良好,其最大误差为8.5%,从而验证了本文一维流动模型假设及计算方法在更高速度条件下的准 确性。
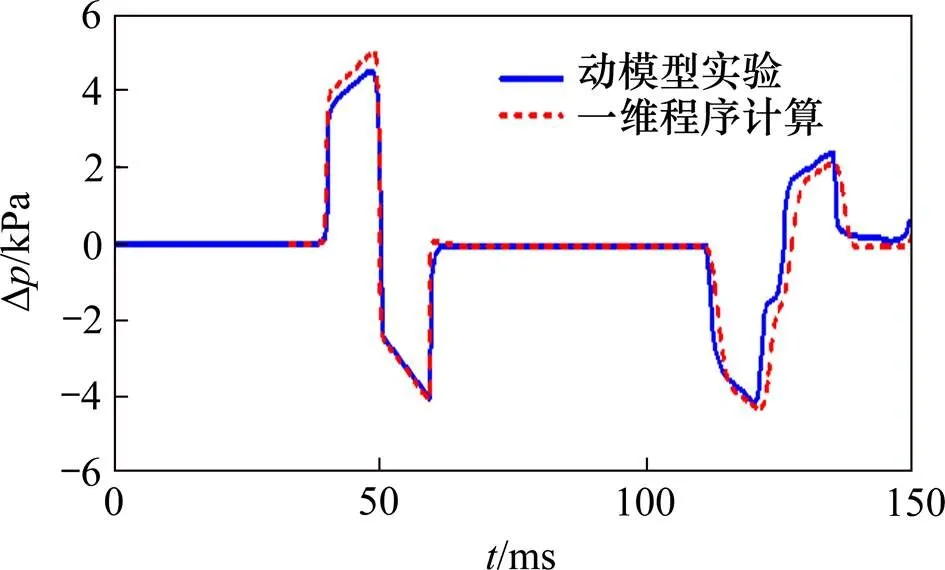
图1 隧道内距进口端2.35 m处静压随时间变化历程
3 计算结果分析
3.1 计算参数
本文以我国某型高速磁浮列车为研究对象,进行单列车通过隧道时车外压力波数值模拟研究,表1表示一维计算程序主要输入参数。
在一维流动模型中采用压力损失系数来表示车头、车尾流线型外形对流动的影响[24]。车头压力损失系数通过采用初始压缩波的求解公式反求得到;车尾压力损失系数采用流体力学突扩公式进行求解。列车壁面摩擦因数通过采用计算车体压力损失的公式来反求得到。当列车驶出隧道后,隧道内的介质仍然有速度,而且速度会不断衰减,直到变为零,因此,根据介质速度在隧道内的衰减来确定隧道壁面摩擦因数。
3.2 隧道内压力波一维平面波特征
图2表示磁浮列车驶入隧道过程中初始压缩波形成阶段隧道壁面和车体表面的压力分布,其中,隧道长度TU=500 m,隧道净空面积TU=140 m2,隧道横截面当量水力半径=6.68 m,鼻长=16.5 m,车高4.2 m,长细比λ=7.9。=0.096 s,0.192 s分别表示列车驶入隧道1个鼻长的距离、驶入隧道2个鼻长的距离。可以发现,在初始压缩波形成阶段,由于磁浮列车流线型外形及变截面的影响,隧道壁面及列车表面压力分布具有三维特征,但是研究表明,随着列车的逐渐驶入,初始压缩波形成,且逐渐脱离车体影响,压力波由三维特征变为一维特征,此时,压力波在隧道内具有一维特性[25]。图2中磁浮列车驶入隧道内约36 m(5.39)后,初始压缩波脱离车体影响,由三维波变成一维平面波。

表1 一维计算程序主要输入参数
图3(a)表示距隧道入口端300 m处测点压力及压力梯度的变化。对于测点处压力时间历程曲线而言,一维数值计算与三维数值计算结果整体趋势吻合良好,对于初始压缩波最大值的计算两者差异较小,在1.43 s初始压缩波达到最大值,两者相差4.2%。对于测点的压力梯度而言,由于一维流动模型采用压力损失系数来近似处理车头流线型变横截面积部分对流动的影响;在车头头部进入隧道过程中,一维和三维得到的压力梯度存在较大的差异,在0.88 s取得最大压力梯度,两者最大差异为39.2%。但图3(b)表示第3节车厢车身中部测点压力变化,两者数值计算结果最大相差为5.3%。综上分析,再结合日本动模型试验验证,本文采用一维可压缩非定常不等熵流动模型来进行车体压力载荷数值计算是准确、经济、合理可行的。

(a) t=0.096 s;(b) t=0.192 s

(a)距隧道入口端300 m处测点压力时间历程曲线;(b)车身中部测点压力变化
3.3 隧道压力波特征
磁浮列车通过隧的过程中引起了隧道内复杂的压力场。列车车头驶入或驶出隧道端口会产生压缩波。类似地,列车车尾驶入或驶出隧道将产生膨胀波。压缩波与膨胀波在隧道内相互叠加,形成了复杂的隧道压力波,且以声速在隧道内传播。对于同类性质的波,波叠加将会强化波的变化幅值,在极短的时间内引起了剧烈的压力梯度。图4表示单列车以200,450和600 km/h的速度通过3 000 m隧道时头车、中间车及尾车车体中部测点的压力波变化特征。可以发现,列车低速通过隧道时,由于压缩波与膨胀波在隧道端口反射次数较多,导致车外压力波动较为剧烈,但是压力波变化幅值远远小于高速通过时的情形。图5给出了不同速度等级下车外压力幅值。列车以600 km/h的速度通过隧道时,车外压力远大于低速通过时的情形,最大压力峰峰值出现在中间车,其值为13.93 kPa;且列车通过隧道的全过程阶段车外压力几乎处于负压区域,最大负压值远大于最大正压值,车体受“膨胀状态”的时间历程远长于车体受“压缩状态”的时间历程。

(a) 头车;(b) 中间车;(c) 尾车

(a) 最大正压值;(b) 最大负压值;(c) 最大压力峰峰值
3.4 隧道长度对车外压力波的影响特性
本小节主要以头尾车车体中部测点为研究对象,研究隧道长度对车外压力波的影响特性,归纳出时速500~600 km/h速度下基于最大正负值和最大压力峰峰值的最不利隧道长度。
图6和图7表示隧道长度对头尾车车体中部测点压力变化幅值的影响特性,TU表示隧道长度。可以发现,当隧道长度在一定范围内时,随着隧道长度的增加,头车最大正压值逐渐增加,之后,随着隧道长度的增加,头车最大正压值保持不变;对头车最大负压值和最大压力峰峰值而言,随着隧道长度的增加,两者的值呈现出先增大,之后逐渐减小的变化趋势。尾车最大正压值和头车相比,变化规律有较大差异,当隧道长度在一定范围内时,随着隧道长度的增加,尾车最大正压值先增大后减小,在此之后,随着隧道长度的增加,尾车最大正压值保持不变;尾车最大负压值和最大压力峰峰值呈现出和头车相同的变化趋势。基于图6和图7中隧道长度对车外压力的影响特性分析,表2统计给出了头尾车分别基于最大正负压值和最大压力峰峰值所对应的最不利隧道长度及车外压力载荷,可为车体强度设计提供一定的数据参考。
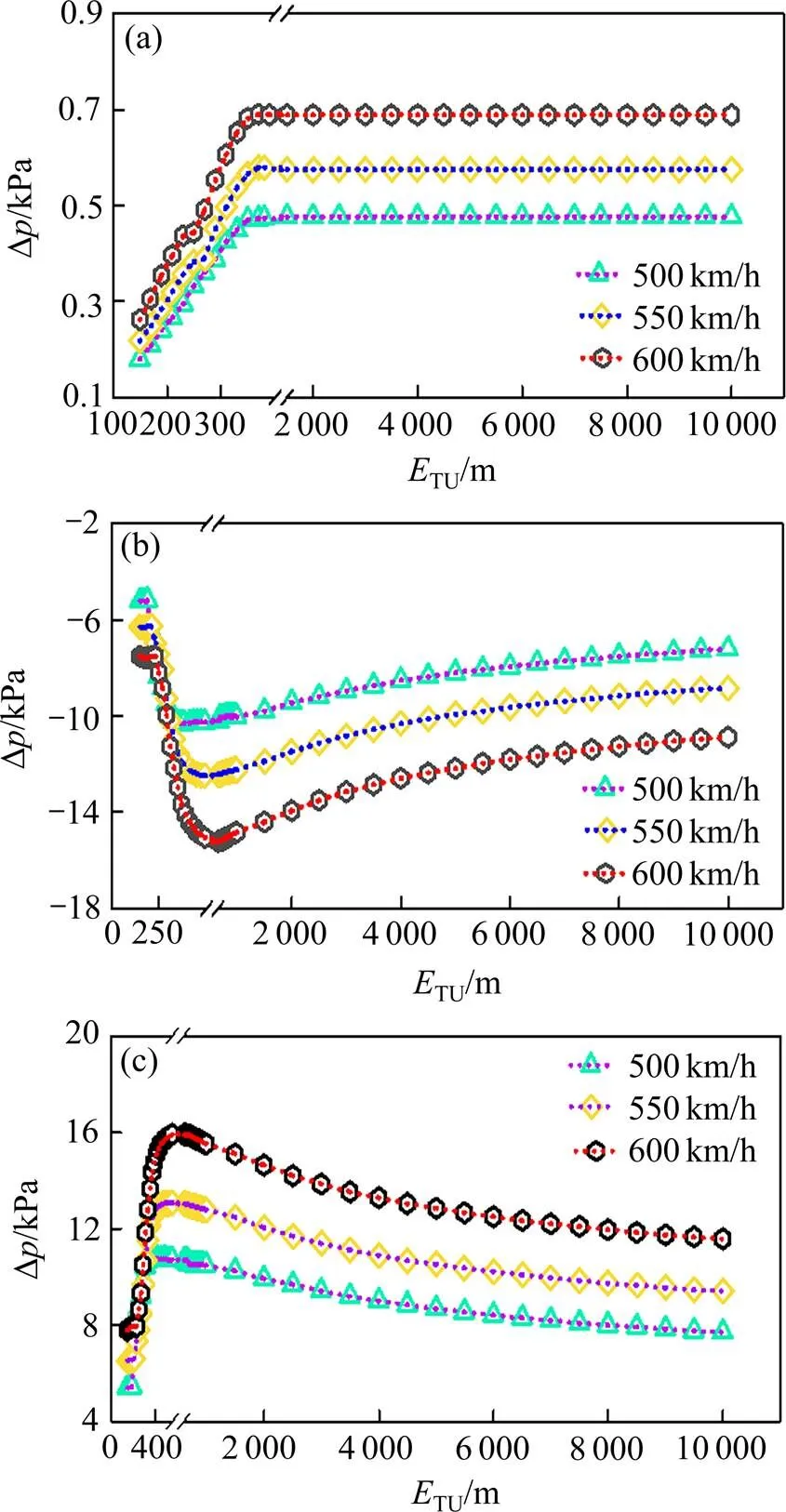
(a) 头车最大正压值;(b) 头车最大负压值;(c) 头车最大压力峰峰压值

(a) 尾车最大正压值;(b) 尾车最大负压值;(c) 尾车最大压力峰峰压值
3.5 速度对车外压力的影响特性
本小节研究磁浮列车以500,550和600 km/h的速度通过3 000 m隧道时车外压力波变化特征。图8表示列车以3种速度通过3 000 m隧道时头尾车车体中部测点压力变化特征,随着列车运行速度的增加,最大正压值、最大负压值均增大;相比之下,速度对车外最大负压值影响更为明显。
图9表示以头车车体中部测点为研究对象,进一步分析不同隧道长度下车外压力变化幅值与运行速度之间的关系,限于篇幅原因,仅展示了头车最大正压值与运行速度之间的关系。根据图9能够拟合出头车最大压力幅值和速度之间的关系(如表所示)形如:
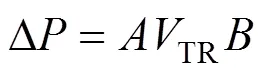

表2 时速500~600 km/h速度下基于最大正负值和最大压力峰峰值的最不利隧道长度统计
(a) 头车;(b) 尾车
图8 不同速度下车外压力时间历程曲线
Fig. 8 Time history curves of external pressure at different speed levels
根据表3可以发现:对于头车最大正压值,的变化范围为0.757~1.986,且随着隧道长度的逐渐增加,的值逐渐增加,最后的值稳定在2左右;对于头车最大负压值,的变化范围为1.083~2.112,且随着隧道长度的逐渐增加,的值逐渐增加,最后的值同样稳定在2左右;同时也可以发现,头车最大正压值与速度的平方成正比的必要性前提是隧道长度与列车长度之比大于5.18,即TU/TR≥5.18;头车最大负压值与速度的平方成正比的必要性前提是隧道长度与列车车长之比大于2.53,即TU/TR≥2.53;因此,可以推测出:全列车车外压力变化幅值和速度的平方成正比这种变化规律和隧道长度及车长密切相关。
3.6 阻塞比对车外压力的影响特性
阻塞比同隧道长度、列车运行速度一样,也是影响车外压力波的主要参数,分别研究列车速度为500,550和600 km/h,隧道净空面积为80,100和140 m2,隧道长度3 000 m。
基于以上工况,将头车车体中部测点作为研究对象,图8表示不同阻塞比下车外压力最值变化特征,TU表示隧道长度。可以发现:阻塞比越大,车外压力最值越大,且对于最大负压值、最大压力峰峰值而言,随阻塞比的增加,呈现出线性增加的变化规律。

表3 车外压力最值−速度 拟合曲线统计

图9 速度对车外压力影响特性(头车最大正压值)
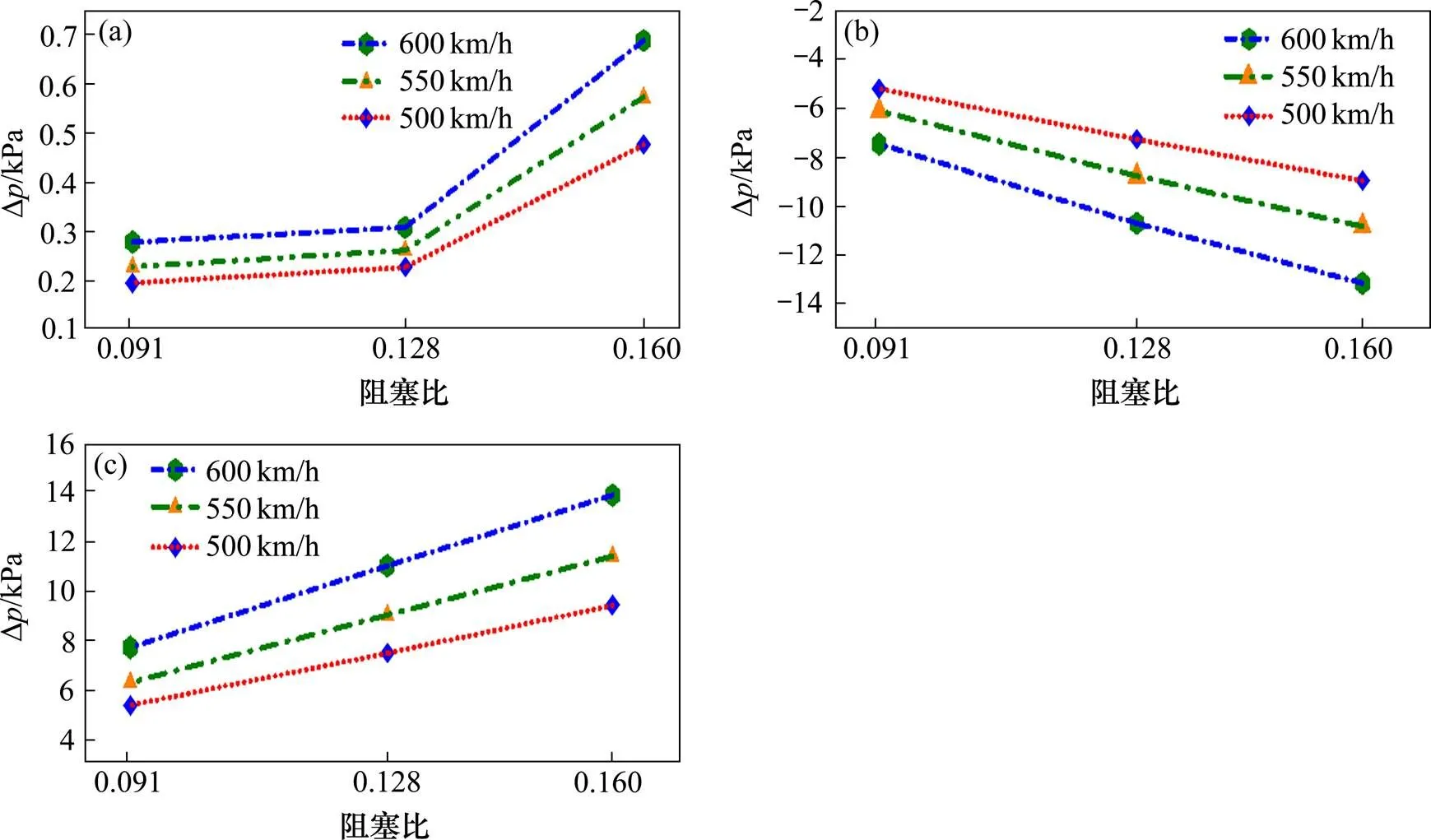
(a) 最大正压值;(b) 最大负压值;(c) 最大压力峰峰值
4 结论
1) 通过分析隧道长度对车外压力变化幅值的影响特性分析,总结了时速500~600 km/h速度下基于最大正负值和最大压力峰峰值的最不利隧道长度。
2) 通过对车外压力变化幅值与列车运行速度之间的研究,发现隧道长度和车长之比超过一定值时,车外压力变化幅值近似与速度的平方成正比的规律方可成立。
3) 通过对车外压力变化幅值与阻塞比之间的研究,阻塞比越大,车外压力最值越大,且对于最大负压值、最大压力峰峰值而言,随阻塞比的增加,呈现出线性增加的变化规律。
[1] 马光同, 杨文姣, 王志涛, 等. 超导磁浮交通研究进展[J]. 华南理工大学学报(自然科学版), 2019, 47(7): 68−74, 82. MA Guangtong, YANG Wenjiao, WANG Zhitao, et al. Research progress of superconducting maglev transportation[J]. Journal of South China University of Technology (Natural Science Edition), 2019, 47(7): 68−74, 82.
[2] 邓旺强. 我国时速600 km高速磁浮试验样车下线[J].高科技与产业化, 2019, 278(7): 14−15. DENG Wangqiang. The 600 km/h high-speed maglev test vehicle is offline in China[J]. High Technology and Industrialization, 2019, 278(7): 14−15.
[3] 韩运动, 姚松, 陈大伟, 等. 基于实车试验的高速列车隧道压力波影响因素[J]. 中南大学学报(自然科学版), 2017, 48(5): 1404−1412. HAN Yundong, YAO Song, CHEN Dawei, et al. Influencing factors of pressure wave in high-speed train tunnel based on actual vehicle test[J]. Journal of Central South University (Science and Technology), 2017, 48(5): 1404−1412.
[4] 田红旗. 中国高速轨道交通空气动力学研究进展及发展思考[J]. 中国工程科学, 2015, 17(4): 30−41. TIAN Hongqi. Research progress and development thinking of aerodynamics of high-speed rail transit in China[J]. China Engineering Science, 2015, 17(4): 30− 41.
[5] Schetz J A. Aerodynamics of high-speed trains[J]. Annual Review of Fluid Mechanics, 2001, 33(1): 371−414.
[6] Ravn S, Reinke P. Tunnel aerodynamics of the magnetic levitation high-speed link in Munich (MAGLEV)– consequences for pressure comfort, micro pressure waves, traction power and pressure loads[J]. Tunnel Management International Journal, 2006, 9(1): 1−10.
[7] Howell J P. Aerodynamic response of maglev train models to a crosswind gust[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1986, 22(2−3): 205−213.
[8] Tielkes T. Aerodynamic aspects of maglev systems[C]// Deutsche Bahn A G, D B Systemtechnik, Dep. of Aerodynamics and Air Conditioning. 19th International Conference on Magnetically Levitated Systems and Linear Drives. Munich, Germany: Dresden, 2006: 1−9.
[9] Yamamoto K, Kozuma Y, Tagawa N, et al. Improving maglev vehicle characteristics for the Yamanashi test line[J]. Qr of Rtri, 2005, 45(1): 7−12.
[10] 山崎幹男, 加藤覚, 若原敏裕, 等. 超高速鉄道トンネル内の圧力変動に対する覆工構造の設計[J]. 土木学会論文集, 2004, 2004(752): 119−131. Yamazaki M, Kato S, Wakahara T, et al. Design of a tunnel lining versus pressure fluctuation in high-speed train tunnel[J]. Journal of Japan Society of Civil Engineers, 2004(752): 119−131.
[11] 高橋和也, 本田敦, 野澤剛二郎, 等. 超高速鉄道トンネルにおける入口側円型緩衝工の微気圧波低減効果[J]. 土木学会論文集 A1(構造・地震工学), 2015, 71(2): 167−172. Takahashi K, Honda A, Nozawa K, et al. Reduction of a micro-pressure wave by a round hood at a tunnel portal of a High-Speed railway[J]. Journal of Japan Society of Civil Engineers, A1: Structural Engineering & Earth-quake Engineering (SE/EE), 2015, 71(2): 167−172.
[12] 本田敦, 高橋和也, 野澤剛二郎, 等. 超高速鉄道トンネルにおける微気圧波の評価および緩衝工の提案. 土木学会論文集 A1 (構造・地震工学), 2015, 71(3): 327−340. Honda A, Takahashi K, Nozawa K, et al. Proposal of a porous hood for a High-Speed railway tunnel based on an evaluation of a micro-pressure wave[J]. Journal of Japan Society of Civil Engineers, A1: Structural Engineering & Earthquake Engineering (SE/EE), 2015, 71(3): 327−340.
[13] Saito S, Iida M, Kajiyama H. Numerical simulation of 1-D unsteady compressible flow in railway tunnels[J]. Journal of Environment and Engineering, 2011, 6(4): 723−738.
[14] 刘堂红, 田红旗, 王承尧. 不同磁浮列车外形的气动性能比较[J]. 国防科技大学学报, 2006, 28(3): 94−98. LIU Tanghong, TIAN Hongqi, WANG Chengyao. Comparison of aerodynamic performance of different maglev train shapes[J]. Journal of National University of Defense Technology, 2006, 28(3): 94−98.
[15] 李颢豪, 杨明智, 孔学舟. 不同高度声屏障对磁浮列车气动效应影响研究[J]. 铁道科学与工程学报, 2017, 14(4): 819−826. LI Haohao, YANG Mingzhi, KONG Xuezhou. Research on the influence of different height sound barriers on aerodynamic effect of maglev trains[J]. Journal of China Railway Society and Engineering, 2017, 14(4): 819−826.
[16] 黄尊地, 梁习锋, 常宁. 真空管道交通列车气动阻力数值分析[J]. 机械工程学报, 2019, 55(8): 165−172. HUANG Zundi, LIANG Xifeng, CHANG Ning. Numerical analysis of aerodynamic resistance of vacuum pipeline traffic trains[J]. Journal of Mechanical Engineering, 2019, 55(8): 165−172.
[17] HUANG S, LI Z, YANG M. Aerodynamics of high-speed maglev trains passing each other in open air[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 188(5): 151−160.
[18] 谈畅达, 周丹. 编组长度对磁浮车边界层及尾流流动的影响[C]// 中国力学学会、浙江大学.中国力学大会论文集(CCTAM 2019). 中国力学学会、浙江大学: 中国力学学会, 2019: 925−933. TAN Changda, ZHOU Dan. The effect of marshalling length on the boundary layer and wake flow of maglev vehicle[C]// Chinese Society of Mechanics, Zhejiang University. Proceedings of the Chinese Society of Mechanics (CCTAM 2019). Chinese Society of Mechanics, Zhejiang University: Chinese Mechanics Society, 2019: 925−933.
[19] 王国静, 张福李, 徐亚之, 等. 160 km/h新型中速磁浮交通列车的车体强度分析[J]. 城市轨道交通研究, 2019, 22(9): 50−52. WANG Guojing, ZHANG Fuli, XU Yazhi, et al. Car body strength analysis of 160 km/h new medium speed maglev traffic train[J]. Research on Urban Rail Transit, 2019, 22(9): 50−52.
[20] 王兆祺, 赵毅山. 磁悬浮列车通过隧道时空气阻力的计算方法[J]. 同济大学学报(自然科学版), 2003, 31(10): 1183−1187. WANG Zhaoqi, ZHAO Yishan. Calculation method of air resistance when maglev train passes through tunnel[J]. Journal of Tongji University (Natural Science Edition), 2003, 31(10): 1183−1187.
[21] 张光鹏, 雷波, 李琼. 磁浮列车气密性能对隧道净空面积的影响[J]. 铁道学报, 2005, 27(2): 126−129. ZHANG Guangpeng, LEI Bo, LI Qiong. Influence of Airtightness of maglev train on clearance area of tunnel[J]. Journal of the China Railway Society, 2005, 27(2): 126−129.
[22] TB 10630—2019, 磁浮铁路技术标准(试行)[S]. TB 10630—2019, Technical standards of the maglev railway (trial)[S].
[23] 梅元贵. 高速铁路隧道空气动力学[M]. 北京: 科学出版社, 2009: 65−94. MEI Yuangui. Aerodynamics of high-speed railway tunnels[M]. Beijing: Science Press, 2009: 65−94.
[24] William-Louis M, Tournier C. A wave signature based method for the prediction of pressure transients in railway tunnels[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2005, 93(6): 521−531.
[25] 梅元贵, 赵汗冰, 陈大伟, 等. 时速600 km磁浮列车驶入隧道时初始压缩波特征的数值模拟[J]. 交通运输工程学报, 2020, 20(1): 120−131. MEI Yuangui, ZHAO Hanbing, CHEN Dawei, et al. Numerical simulation of initial compression wave characteristics when a maglev train with a speed of 600 km per hour enters a tunnel[J]. Journal of Transportation Engineering, 2020, 20(1): 120−131.
Pressure load characteristics of high-speed maglev single-track tunnels
ZHANG Zhichao1, DU Jian2, ZHAO Hanbing1, MEI Yuangui1
(1. Gansu Province Engineering Laboratory of Rail Transit Mechanics Application Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. CCRC Qingdao Sifang Co., Ltd., Qingdao 266111, China)
The high-speed maglev trains could cause severe pressure fluctuations when passing through tunnels, thus resulting in discomfort to the ears of drivers and passengers, and leading to aerodynamic fatigue life problems of train bodies and other components of trains, linings and auxiliary facilities of tunnels. It is necessary to study the pressure wave effect of high-speed maglev trains passing through tunnels. In this paper, the one-dimensional compressible unsteady non-homentropic flow model and method of characteristics of generalized Riemann variables were used to numerically study the pressure load of a train body when a single train passes through a tunnel. The effect laws of tunnel length, train speed, and blocking ratio on the external pressure wave were revealed. The most critical tunnel length based on the maximum positive and negative values and the maximum pressure peak-to-peak value at the speed of 500 to 600 km/h was obtained. It is demonstrated the applicable range of the pressure wave amplitude generated by the train passing through the tunnel is directly proportional to the square of the train speed. The fitting relation between the maximum pressure and speed was summarized. The research methods and results in this paper can provide a reference for the selection of aerodynamic loads for train body design.
high-speed maglev train; tunnel; pressure waves; train body aerodynamic load; character method of one-dimensional flow model

U451.3;V211.3
A
1672 − 7029(2021)01 − 0021 − 10
10.19713/j.cnki.43−1423/u.T20200201
2020−03−14
国家重点研发计划资助项目(2016YFB1200602-39)
梅元贵(1964−),男,河南荥阳人,教授,博士,从事列车空气动力学;E−mail:meiyuangui@163.com
(编辑 蒋学东)

