基于Peck公式的盾构隧道施工引起的地层三维沉降预测

张运强，曹文贵，周苏华，周帅康，邢静康，黄郁东

基于Peck公式的盾构隧道施工引起的地层三维沉降预测

张运强，曹文贵，周苏华，周帅康，邢静康，黄郁东

(湖南大学 土木工程学院，湖南 长沙 410082)

盾构隧道施工会诱发地层沉降，合理地预测地层沉降对于保护邻近地下结构具有重要意义。首先，通过分析地表与地表以下深层土体的沉降规律，建立二者之间的联系；然后，基于Peck公式，通过引入不同种类土体的参数，掌子面地表位移释放率以及地表纵向沉降最大斜率，提出不同种类土体中单、双洞盾构隧道施工诱发地层三维沉降的计算公式；最后，利用工程实测数据进行了对比验证，并对相关参数影响规律进行了简要分析。研究结果表明：本文方法与实测数据吻合良好，验证了该方法的准确性和适用性；合理的控制先、后行隧道开挖距离可以有效地减小掌子面土体沉降；地层沉降槽形态变化系数()可以较好地预测双洞隧道开挖时任一深度土体沉降槽的形态。文末通过对大量实测数据分析，给出了相关参数的取值范围，可为无工程经验地区提供参考。

盾构隧道；Peck公式；三维地层沉降；土体损失

隧道施工会改变原有土体的应力状态，进而引发地表和深层土体的沉降。城市盾构隧道不可避免的会穿越大量已存在的地下结构(如地下管线、隧道、建筑物基础等)，过度的地层沉降势必会对既有地下结构安全造成威胁。目前，关于地表沉降预测已经有了较为丰硕的研究[1−5]，然而，由于地表以下深层土体的最大沉降要大于地表且沉降槽宽度随着土体深度的增加而变窄[6]，致使邻近地下结构在隧道施工过程中可能会经历更大的角变形[7]。因此，合理的盾构隧道施工诱发的深层土体沉降对于保护邻近地下结构具有较为重要的意义。1969年，Peck[5]首次提出用高斯曲线去描述隧道开挖引起的地表沉降槽，并提出了隧道开挖诱发地表沉降的经验公式。Mair等[8]通过分析隧道开挖引起的地表和地下沉降槽，发现地下沉降槽同样满足高斯分布，并基于此提出了黏土中地下沉降槽宽度的计算方法。韩煊等[9]通过对国内多组隧道开挖实测沉降数据的分析，发现这些数据均能较好地满足高斯分布，并对Mair提出地下沉降槽宽度计算公式进行了修正。FANG等[7]采用统计地下沉降实测值的方法，给出了基于地表沉降数据的地下沉降槽预测方法，然而，随着深度的增加，地下沉降槽误差将不断增大。陈春来等[10]基于前人建立的沉降槽宽度计算公式，提出了深层土体三维沉降的计算公式，但未对深层土体沉降进行实质性验证。基于上述研究存在的问题，本文通过分析地表与地下深层土体的沉降规律，建立了地表及地下最大沉降和对应沉降槽宽度之间的函数关系，然后通过引入考虑不同类型土体的参数，掌子面地表位移释放率以及地表纵向沉降最大斜率，提出了不同种类土层中单、双洞隧道施工诱发地层三维沉降的计算公式，并对相关参数影响和无工程经验地区的参数取值进行了讨论和分析。

1 单洞盾构隧道施工引起沉降计算

1.1 二维沉降

Peck[5]基于对实测数据统计分析基础之上，首次提出地表沉降槽曲线遵循高斯分布，认为土体移动由土体损失产生，并假设土体不排水且沉降槽体积等于土体损失体积。由于Peck公式物理意义明确且参数少，成为预测单洞隧道施工诱发地表沉降的有效、快捷方法。式(1)为单洞盾构隧道开挖诱发横向地表沉降的估算公式

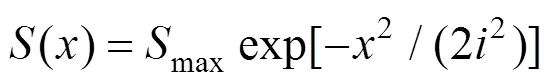
式中：max为地表最大沉降值；为地表任一点距隧道中心水平距离；为沉降槽曲线反弯点至隧道中心水平距离，一般可称为“地表沉降槽宽度”。其中

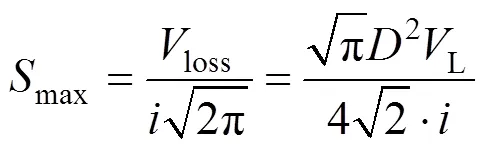
式中：为隧道开挖直径；loss为土体损失体积；L为土体损失率。

O’Reilly等[6]根据伦敦地区的经验，提出了沉降槽宽度与隧道中心埋深0之间存在线性关 系，即

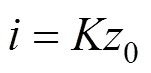
式中：为沉降槽宽度参数，该参数为无量纲参数。

由于隧道开挖诱发的地层沉降会对邻近地下构筑物产生影响，因此，如何预测深层土体的沉降规律至关重要。如图1所示，为单洞隧道开挖诱发的地表和深层土体横向沉降示意图。

Mair等[8]通过对实测数据统计分析，认为隧道开挖引起的深层土体沉降槽宽度与深度有关，计算公式如下：

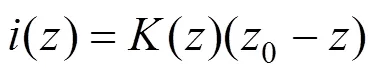
式中：()为地下深度处沉降槽宽度参数。

Mair提出的公式是建立在黏性土的基础上且假定地表处横向沉降槽宽度参数为0.5且不变，具有很大的局限性。基于此，韩煊等[9]在Mair等有关地下沉降槽的研究基础上，提出采用归一化的系数d进行修正，该系数定义如下：

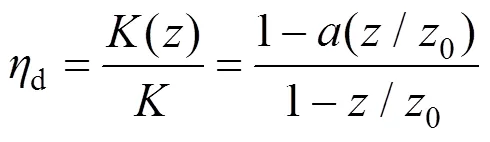
式中：a为考虑不同土质类型的参数，介于0和1之间。当无地区工程经验时，韩煊等[9]建议黏土取a=0.65，砂土取a=0.50。

根据式(5)，可得()与之间关系

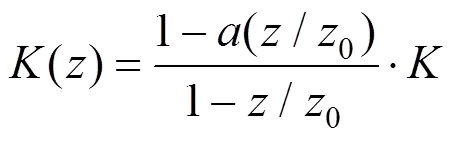
将式(6)代入式(4)即可得()表达式

将式(7)与式(3)两端相除，可得地下深度处与地表沉降槽宽度之间的关系

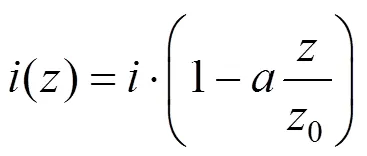
将式(8)代入式(2)，可得深度处的最大沉降值

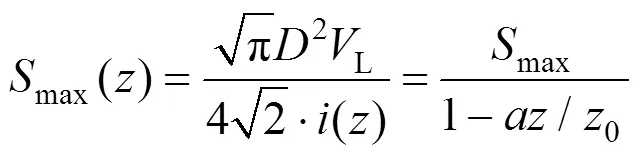
结合式(9)和式(1)即可得深度处的土体二维沉降计算公式，如下式

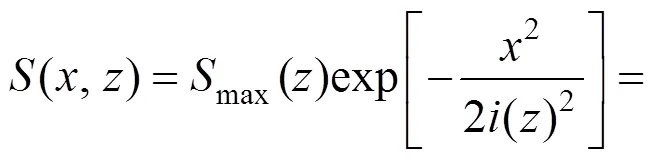
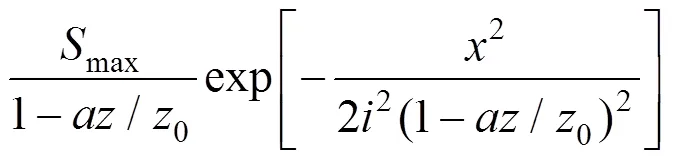
1.2 三维沉降

式(10)仅能反映隧道开挖后盾尾土体瞬时沉降基本稳定时的横向沉降槽，不能计算由此引起的土体纵向沉降。如图2所示，为单洞盾构隧道坐标位置示意图，隧道与轴平行且位于原点正下方0深度处，假设掌子面处坐标=0。图中盾构前进方向与轴的正方向保持一致。

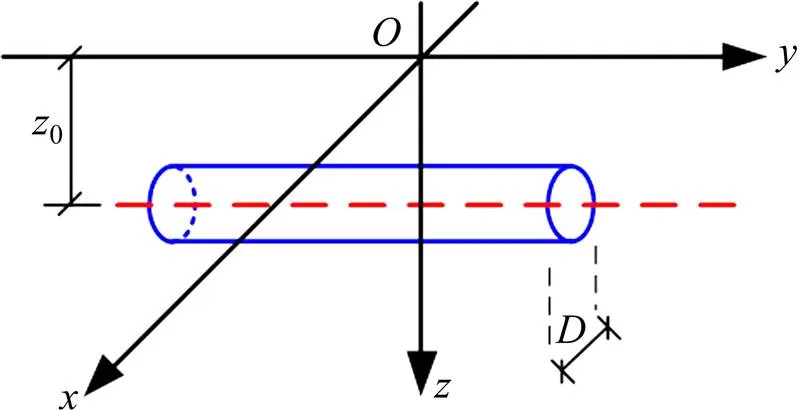
图2 单洞盾构隧道坐标图

Attewell等[11]基于Peck公式，采用累积概率曲线推导得到了隧道轴线正上方的地表纵向沉降计算公式，如下

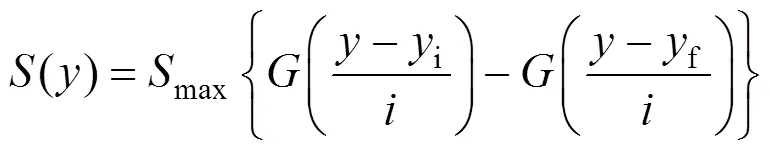
式中：y为隧道的起点位置；f为隧道的终点位置；为概率函数。

Attewell等[11]提出的地表纵向沉降槽计算公式中，掌子面处的沉降始终为地表最大沉降的50%，这与实际不符。佘方涛等[12]通过分析其不足，引入掌子面地表位移释放率和地表纵向沉降最大斜率2个特征值，提出了修正的地表纵向沉降计算公式

其中：

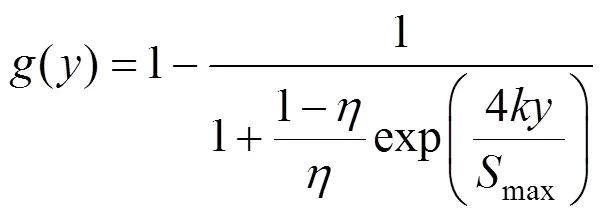
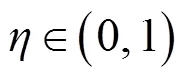
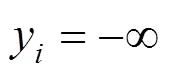
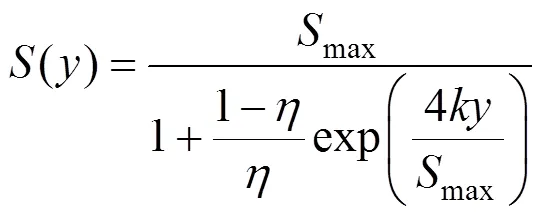
结合式(10)和(14)，即可得单洞隧道盾构施工引起的地表及深层土体的三维沉降计算公式

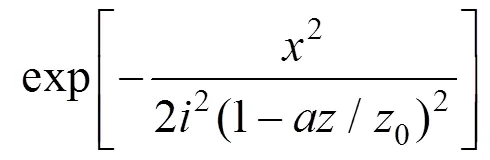
对于参数V和以及，的取值，可将式(1)和式(14)分别转换为式(16)和式(17)形式

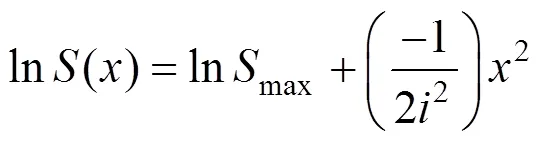
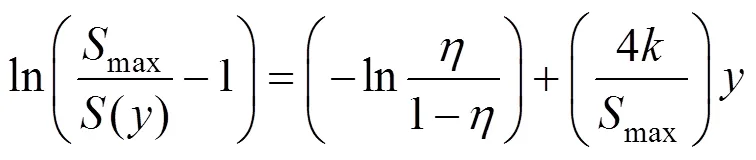
利用式(16)和式(17)并结合式(2)，通过地表实测数据运用线性最小二乘法可以得到上述4个参数，参数按照韩煊[9]一文取建议值。需要指出的是，由于地铁隧道埋深一般较浅，故文中忽略了地下水的影响。

2 双洞盾构隧道施工引起的沉降计算

2.1 二维沉降

城市的隧道建设当中多数以双线水平平行盾构隧道的形式出现，本节重点研究双线水平平行盾构隧道施工诱发的地层沉降。如图3所示，为双洞水平平行隧道开挖诱发的地表和深层土体横向沉降槽示意图。

刘波等[1]基于叠加原理，得到双洞平行隧道开挖引起的地表横向沉降计算公式，如下

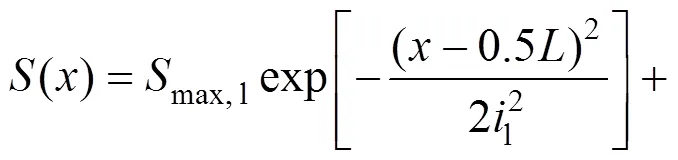
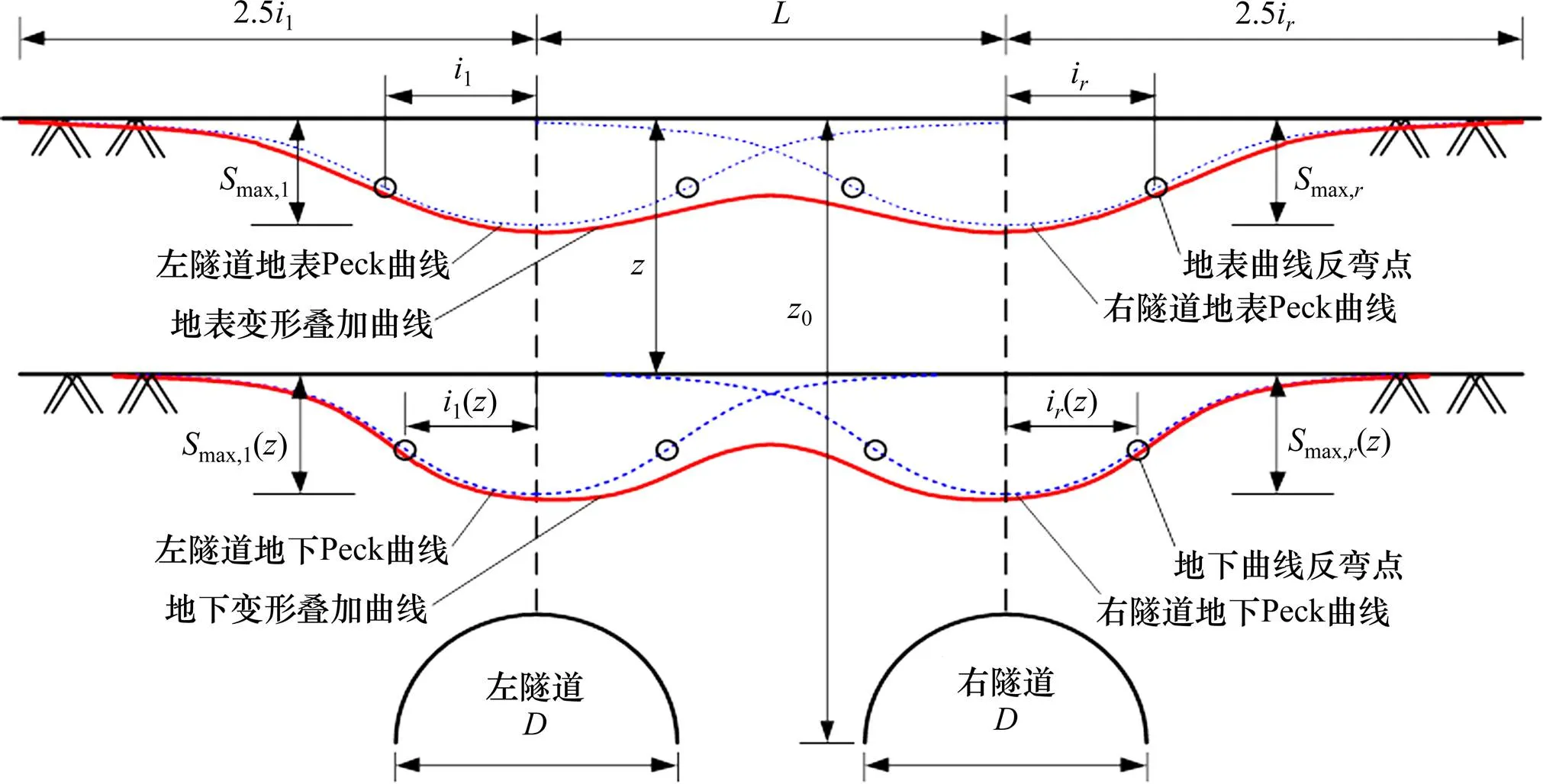
图3 双隧道施工地层变形示意图

按照单洞隧道的求解思路，可得双洞水平平行盾构隧道施工时，深度处土体的二维沉降计算 公式

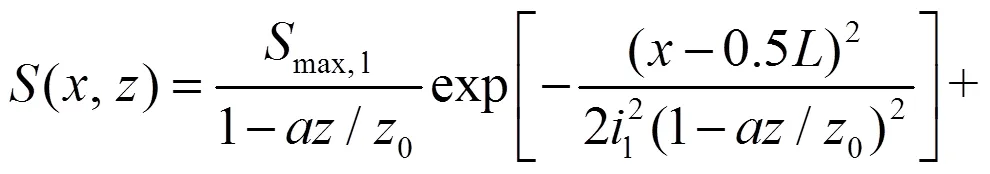
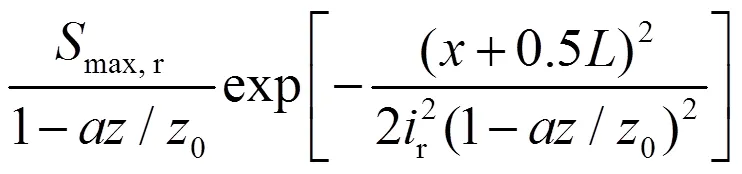
2.2 三维沉降

如图4所示，为双洞盾构隧道坐标位置示意图，隧道前进方向与轴平行且两隧道中间水平中轴线位于坐标原点正下方0深度处，假设掌子面处坐标为0点，即=0。图中盾构前进方向与轴的正方向保持一致。

图4 双线平行盾构隧道坐标图

根据叠加原理并采用与单洞隧道同样的分析方法，可以得到双洞水平平行隧道施工引起的地表及深层土体的三维沉降计算公式

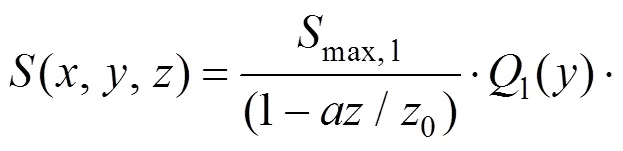
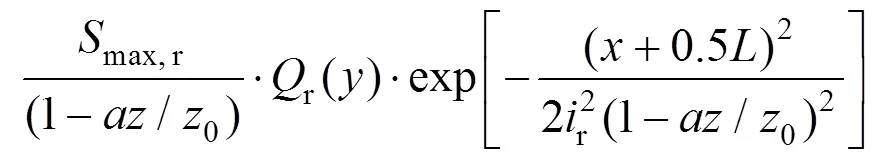
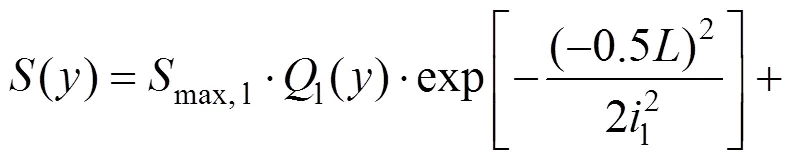
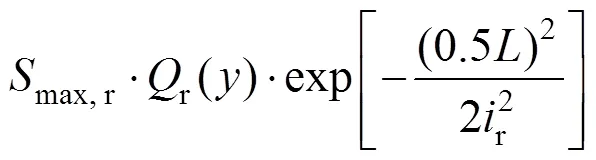
3 实例验证及参数分析

3.1 单洞盾构隧道工程实例分析

取文献[2]中工程实例进行验证分析。表1为根据地表实测数据反分析得到的计算参数。

表1 地表实测数据反分析参数

实例：台北捷运系统(TRTS)台湾新线CH218合同B1段采用土压平衡盾构机进行开挖。在隧道开挖面以上主要以砂土为主，故参数取0.5。隧道外径为6.05 m，埋深0为18.5 m。取表1中得到的参数，并利用式(15)计算得到地面和地下沉降曲线，如图5所示。文中取=−100 m，表示隧道开挖面已经通过计算断面100 m(此时认为瞬时沉降已基本趋于稳定)。图5为地表和地表以下10 m深度处的沉降实测值与计算值对比图，由图可知，无论地表还是地下10 m处的沉降计算曲线均与实测数据吻合良好。

3.2 双洞盾构隧道工程实例分析

本节取文献[14]中工程实例进行验证分析。表2为根据地表实测数据反分析得到的计算参数。

杭州地铁1号线采用双线水平平行盾构隧道，其中右侧隧道先于左侧隧道施工。研究区段土质以粉质砂土为主，参数取0.5。2条隧道外径均为6.2 m，埋深0为19.0 m，水平间距为12.0 m，采用土压平衡盾构法施工。取表2中得到的参数，并利用式(20)计算得到地面、地下及纵向沉降曲线，如图6和7所示。对于图6中的横向沉降曲线，右侧和左侧隧道均取隧道开挖面通过计算断面100 m，即取右=−100 m，左=−100 m。由图6可知，图6(a)中地表沉降计算曲线与实测数据吻合良好；由于图6(b)实测数据有限，不能准确的表明地下3m和7 m处的沉降计算曲线与实测数据吻合程度，但仅有的2个数据点非常邻近计算曲线，总体上认为吻合效果较良好。

图7为2隧道中轴线正上方(即=0)纵向沉降曲线，由图可知，地表、地下3 m和7 m处纵向沉降计算曲线均与实测数据吻合良好。

3.3 相关参数分析

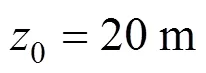
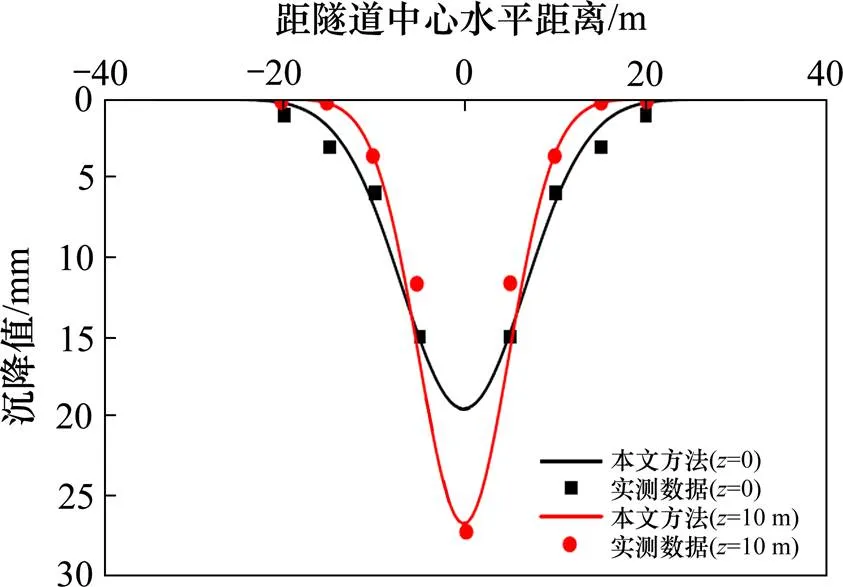
图5 横向沉降计算值与实测值对比

表2 地表实测数据反分析参数

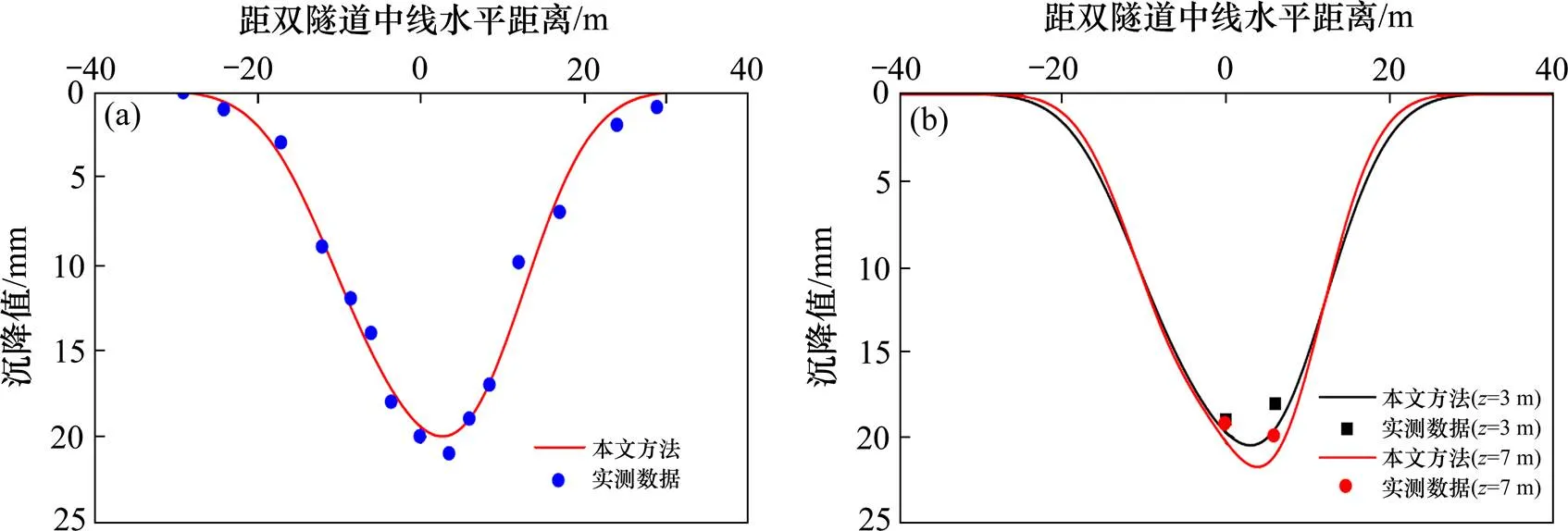
(a) 地表；(b) 地下

(a) 地表；(b) 地下

3.3.1 土体深度影响

如图8所示，为不同深度时的横向沉降曲线，假设左右隧道均已开挖稳定，左右纵向坐标均取=−100 m。由图8可知，随着深度的增加，沉降槽宽度略有减小，最大沉降量增加，但最大沉降量位置由两隧道中心向两侧移动，沉降槽形状逐渐由“单峰”变成“双峰”。宫亚峰等[15]通过对大量的数值试验分析，提出地表沉降槽形状与两隧道水平中心距，沉降槽宽度等因素有关，并给出地表沉降槽形态变化系数，如下：

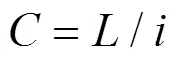
当=2时，为“单峰”和“双峰”的临界值；当=7时，为“双峰”变成相互独立的2个“单峰”的临界值。将式(8)代入式(22)，即可得到地层任一深度沉降槽形态变化系数()：

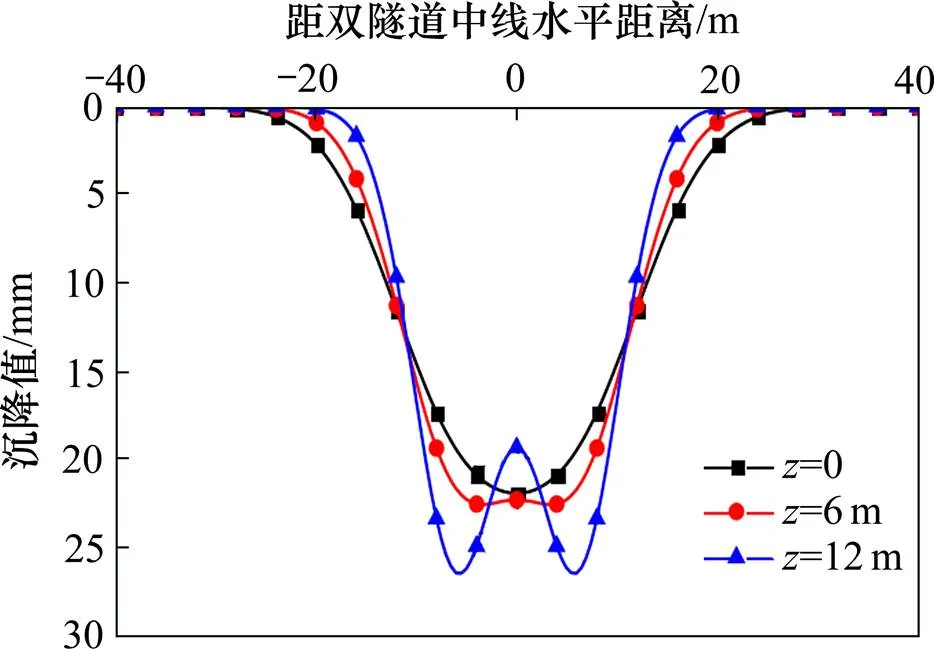
图8 不同土体深度处横向沉降曲线

3.3.2 先行与后行隧道开挖距离影响

如图9所示，为先行与后行隧道不同开挖距离时的地表横向和纵向沉降曲线，假设左隧道先行开挖，右侧隧道后行开挖，沿开挖方向两隧道间距为，左侧纵向坐标取=−100 m，即左隧道沉降已基本趋于稳定。由图9(a)可知，随着的减小，最大沉降值逐渐增大，且最大沉降点逐步驶离左隧道正下方，向右隧道靠近。工程中由于先行隧道已扰动原有土体，故先行隧道侧土体损失率会大于后行一侧，导致最大沉降点偏向先行隧道。图9(b)为2隧道中间位置的纵向沉降曲线，图中以先行隧道为纵向坐标系进行绘制，可以看到随着的减小，纵向沉降曲线形态发生明显变化，沉降幅度由缓逐渐变陡。因此，工程中应合理控制先、后行隧道开挖距离以减小开挖过程中的瞬时沉降。

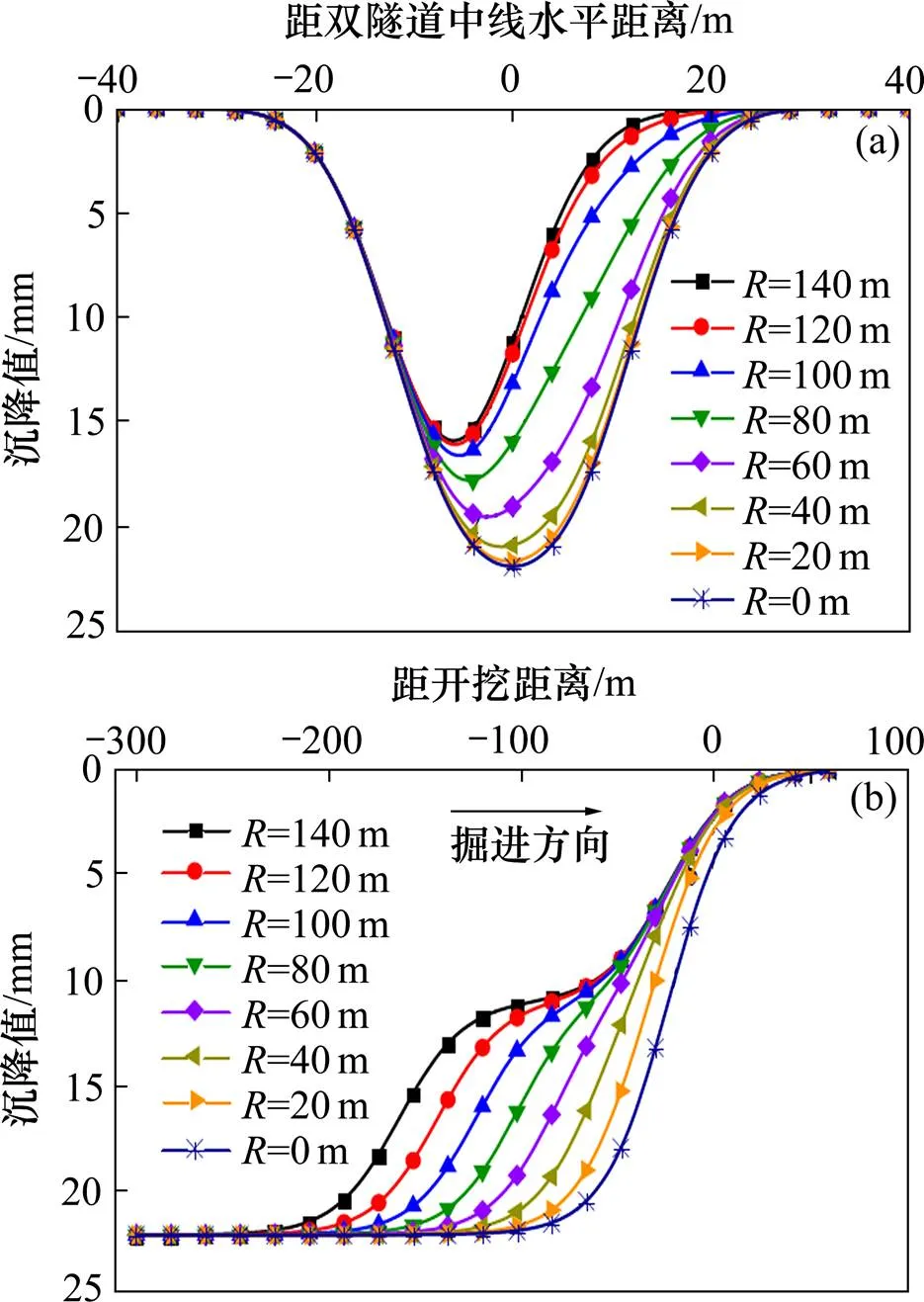
(a) 横向沉降；(b) 纵向沉降

图10 不同隧道间距时地表横向沉降曲线

3.3.3 隧道水平中心距影响

如图10所示，为隧道不同水平间距时的地表横向沉降曲线，取左右纵向坐标为=−100 m。由图10可知，随着增加，沉降槽宽度逐渐增大，而最大沉降值逐渐减小，沉降槽曲线形状由“单峰”逐渐变成“双峰”。采用式(23)进行计算，可得“单峰”和“双峰”的临界值为14 m，这与图10吻合。

4 讨论

本文提出的地层三维沉降预测方法实际运用中主要可针对以下3个方面：1) 利用易监测的地表沉降槽数据预测难监测的地下沉降槽曲线；2) 利用已开挖的地表沉降监测数据预测前方未开挖的地表及地下沉降；3) 利用工程经验数据预测无工程经验地区隧道开挖引起的地表及地下沉降。虽然目前有关地表沉降的预测已经有了长足的发展，但诸如参数，L，和等受施工方法和技术水平等影响很大，且在实际工程中地层并非均一，故对未知区域进行沉降预测时，很难选择较为合适的计算参数。本节通过对大量实测数据[2−4, 14−17]整理分析，给出了不同施工方式下参数，L的箱线图和不同土质下参数，的箱线图，并对各参数的主要分布区间(即25%～75%区间)进行了分析。如图11所示，对比3种施工方法可知，泥水平衡盾构施工时沉降槽宽度参数和土体损失率L均最小，主要分布区间分别为0.31～0.51和0.18～0.82；土压平衡盾构与浅埋暗挖法施工时沉降槽宽度参数的主要分布区间分别为0.41～0.59和0.41～0.61，土体损失率L的主要分布区间分别为0.74～1.19和0.47～1.21，采用土压平衡盾构施工时参数分布范围更为集中。图12为不同土质下参数，的箱线图，可以看到黏土和砂土中的掌子面地表位移释放率的主要取值区间分别是0.16～0.25和0.26～0.51，这与文献[16]的结果(0.15～0.25和0.30～0.50)近似。对于地表纵向沉降最大斜率，图中显示黏土和砂土中的主要分布区间分别为0.46～0.80和0.14～0.88，但因其不仅与土质有关，同时与隧道直径和埋深等相关，具体使用时应需要进行更为深入的研究。

图11 不同施工方式下参数K，VL箱线图

图12 不同土质下参数η，k箱线图

5 结论

1) 通过与工程实测数据对比，验证了本文所提单、双洞盾构隧道施工引起的地层三维沉降计算公式的合理性。主要应用在以下3个方面：利用易监测的地表沉降预测难监测的地下沉降；利用已开挖的地表沉降监测数据预测前方未开挖的地表及地下沉降；利用工程经验数据预测无工程经验地区隧道开挖地表及地下沉降。

2) 双隧道地表及地下沉降槽有“单峰”和“双峰”2种形态，提出的地层沉降槽形态变化系数()可以预测双洞隧道开挖时任一深度土体沉降槽的形态；合理的控制先、后行隧道开挖间距可以有效地减小掌子面土体沉降。

3) 3种不同施工方法的和L范围略有不同，采用土压平衡盾构施工时参数和L分布范围较为集中；黏土和砂土中的主要取值区间分别是0.16～0.25和0.26～0.51。

4) 本文未考虑盾构施工时盾壳摩擦以及正面附加推力等引起的土体沉降，且模型未考虑富水地层和非同一水平面上的2个隧道同期或非同期施工的情况，将在今后进行更为深入的研究。

[1] 刘波, 陶龙光, 丁城刚, 等. 地铁双隧道施工诱发地表沉降预测研究与应用[J]. 中国矿业大学学报, 2006(3): 356−361. LIU Bo, TAO Longguang, DING Chenggang, et al. Prediction for ground subsidence induced by subway double tube tunneling[J]. Journal of China University of Mining & Technology, 2006(3): 356−361.

[2] Moh Z C, Ju D H, Hwang R N. Ground movements around tunnels in soft ground[C]// Proc. International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground. London, 1996: 36−42.

[3] 滕丽, 张桓. 盾构穿越砂卵石地层地表沉降特征细宏观分析[J]. 岩土力学, 2012(4): 186−195. TENG Li, ZHANG Huan. Meso-macro analysis of surface settlement characteristics during shield tunneling in sandy cobble ground[J]. Rock and Soil Mechanics, 2012(4): 186−195.

[4] 施成华, 彭立敏. 随机介质理论在盾构法隧道纵向地表沉降预测中的应用[J]. 岩土力学, 2004(2): 153−156. SHI Chenghua, PENG Limin. Application of stochastic medium theory to predicting settlement in longitudinal surface due to tunnel construction by shield[J]. Rock and Soil Mechanics, 2004(2): 153−156.

[5] Peck R B. Deep excavations and tunneling in soft ground[C]// Proceeding of 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: State of the Art Report, 1969: 225−290.

[6] O’Reilly M P, New B M. Settlements above tunnels in the United Kingdom- their magnitude and prediction[C]// Proceedings, Tunneling’82. London: Institution of Mining and Metallurgy, 1982: 137−181.

[7] FANG Y S, WU C T, CHEN S F, et al. An estimation of subsurface settlement due to shield tunneling[J]. Tunnelling and Underground Space Technology, 2014(44): 121−129.

[8] Mair R J, Taylor R N, Bracegirdle A. Subsurface settlement profiles above tunnels in clays[J]. Geotechnique, 1993, 43(2): 315−320.

[9] 韩煊, 李宁, Standing J R. 地铁隧道施工引起地层位移规律的探讨[J]. 岩土力学, 2007(3): 187−191. HAN Xuan, LI Ning, Standing J R. Study on subsurface ground movement caused by urban tunneling[J]. Rock and Soil Mechanics, 2007(3): 187−191.

[10] 陈春来, 赵城丽, 魏纲, 等. 基于Peck公式的双线盾构引起的土体沉降预测[J]. 岩土力学, 2014(8): 2212－2218. CHEN Chunlai, ZHAO Chengli, WEI Gang, et al. Prediction of soil settlement induced by double-line shield tunnel based on Peck formula[J]. Rock and Soil Mechanics, 2014(8): 2212−2218.

[11] Attewell P B, Woodman J P. Predicting the dynamics of ground settlement and its derivatives caused by tunnelling in soil[J]. Ground Engineering, 1982(11): 13−22.

[12] 佘芳涛, 王永鑫, 张玉. 黄土地层地铁暗挖隧道地表纵向沉降规律及其预测分析方法[J]. 岩土力学, 2015(增1): 287−292. SHE Fangtao, WANG Yongxin, ZHANG Yu. Surface longitudinal settlement induced by subway tunneling in loess and its prediction analysis method[J]. Rock and Soil Mechanics, 2015(Suppl 1): 287−292.

[13] MA Ling, LUO Hanbin, CHEN Huarong. Safety risk analysis based on a geotechnical instrumentation data warehouse in metro tunnel project[J]. Automation in Construction, 2013, 34: 75−84.

[14] CHEN R P, ZHU J, LIU W, et al. Ground movement induced by parallel EPB tunnels in silty soils[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 163−171.

[15] 宫亚峰, 王博, 魏海斌, 等. 基于Peck公式的双线盾构隧道地表沉降规律[J]. 吉林大学学报(工学版), 2018, 48(5): 1411−1417. GONG Yafeng,WANG Bo, WEI Haibin, et al. Surface subsidence law of double-line shield tunnel based on Peck formula[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(5): 1411−1417.

[16] 吴昌胜, 朱志铎. 不同隧道施工方法引起地层损失率的统计分析[J]. 浙江大学学报(工学版), 2019, 53(1): 24−35. WU Changsheng, ZHU Zhiduo. Statistical analysis of ground loss ratio caused by different tunnel construction methods in China[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(1): 24−35.

[17] 张书丰, 孙树林, 姜志强. 盾构施工纵向地表沉降分析及基于延迟差分方程的动态预报[J]. 岩土力学, 2008(1): 185−189. ZHANG Shufeng, SUN Shulin, JIANG Zhiqiang. Analysis and dynamic prediction of longitudinal ground settlements due to shield tunneling based on delayed difference equation[J]. Rock and Soil Mechanics, 2008(1): 185−189.

Prediction of three-dimensional subface and subsurface settlement caused by shield tunnelling based on Peck formula

ZHANG Yunqiang, CAO Wengui, ZHOU Suhua, ZHOU Shuaikang, XING Jingkang, HUANG Yudong

(School of Civil Engineering, Hunan University, Changsha 410082, China)

The construction of urban shield tunnel will induce the ground settlement, and reasonable accurate prediction of the ground settlement is of great significance for the protection of adjacent structures. Firstly, based on the analysis of the settlement law of the surface and subsurface, the relationship between the two was established. Then, based on the Peck formula, by introducing the parameterof different types of soil, the surface displacement release rateof the palm surface, and the maximum slope of the vertical settlement of the ground surface, the three-dimensional formation induced by single and double shield tunnels in different types of soil were proposed. Finally, the comparative analysis was made by using the measured data of the project, and the influence law of the relevant parameters was analyzed briefly. The research shows that the method in this paper is in good agreement with the measured data, which verifies the accuracy and applicability of the method. Reasonable control of the excavation distance of the first and the second tunnel can effectively reduce the soil settlement on the face of the tunnel. The coefficient(z) can accurately predict the shape of settlement groove at any depth in double tunnels. At the end of the article, through analysis of a large number of measured data, the value range of relevant parameters is given, which can provide a reference for areas without engineering experience.

shield tunnel; Peck formula; three-dimensional stratum settlement; ground loss

TU443

A

1672 − 7029(2021)01 − 0153 − 09

10.19713/j.cnki.43−1423/u.T20200181

2020−03−07

国家重点研发计划项目(2019YFB1705201)；国家自然科学基金青年基金资助项目(51708199)；中央高校基本科研业务费专项基金资助项目(531107050969)；贵州省科技支撑计划项目(2020-4Y047，2018-133-042)；北京市科技计划项目(Z181100003918005)

周苏华(1987−)，男，江苏盐城人，助理教授，博士，从事岩土工程方面研究；E−mail：zhousuhua@hnu.edu.cn

(编辑 阳丽霞)