横向滑坡作用下埋地管道静力学与数值模拟对比分析
王荣有,张家铭,王 聪
(中国地质大学(武汉)工程学院,武汉 430074)
近年来,随着工业化进程的不断加快,世界各国对石油天然气等能源的需求量不断增加,长输油气管道工程飞速发展,目前已成为该类介质的重要输送手段。但在管道运营过程中,滑坡地质灾害对管道的安全构成了严重的威胁[1]。其中横向滑坡(滑坡滑动方向与埋地管道走向垂直)对埋地管道造成的威胁最大,在这种作用状态下,埋地管道不仅受到拉压作用力,还受到剪切作用力。因此,对横向滑坡作用下埋地管道的受力分析是极其重要的。
中外学者对于埋地管道在滑坡作用下的力学行为进行了深入的研究,Challamel等[2]、Mahdavi等[3]曾利用一种复合的模型对管-土相互作用进行了探讨;O’Rourke等[4]运用Ramberg-Osgood幂指数硬化模型对山体滑坡区域内发生偏移管道的力学模型进行了研究;张坤等[5]利用“Bow-tie”管道塑性变形计算模型,对管道在径向挤压和管内泄漏余压作用下的塑性变形进行分析计算,计算管道挤压所需载荷量;王磊[6]、谢强等[7]、Liu 等[8]、尚玉杰等[9]利用Winkler弹性地基梁模型,推导了横向滑坡作用下管道变形和内力的解析解,且用有限元模拟方法研究了管道受力变形的特性;陈利琼等[10]、薛景宏等[11]运用数值模拟软件,分析了埋地管道穿越滑坡时的应力应变分布规律,并研究了土壤性质、管道外径、壁厚、内压和管材等因素对管道应力应变的影响。此外,将朗肯土压力理论和地基学原理引入滑坡作用下埋地管道力学响应分析,建立横向滑坡作用下管道受力模型也是一种比较合理的尝试[12]。但已有理论在分析横向滑坡作用下管道受力变形特性时,将滑坡作用于管道上的力设成了均布力,没有考虑滑坡推力在横向上的变化,不能反映管道的实际受力状态。
现基于尚玉杰等[9]提出的Winkler弹性地基梁模型和滑坡推力横向分布模型,考虑温差、内压及推力等因素产生的当量轴力的作用,研究在滑坡作用下管道的应力应变分布规律,并与其他算法及有限元方法的计算结果进行对比分析,以期对埋地管道的长期安全运行提供参考。
1 横向滑坡作用下管道力学模型
文献[9]给出了滑坡推力的横向分布模型(图1)及埋地管道受力和变形的力学模型(图2),其中滑坡推力横向分布模型及合力P的表达式为
(1)
式(1)中:P为滑坡作用的合力,N;P0为主滑断面处剩余下滑力,N/m;ymin和ymax分别为滑动方向垂直平面与滑坡边界交点的最小值与最大值,m。
根据滑坡推力横向分布模型,得到横向滑坡作用下埋地管道力学模型,如图2所示。将埋地管道可以简化成受当量轴力和推力作用的梁。在计算之前,对正负号做统一规定:以管道上侧受压为正,轴力以拉力为正。为了计算简便,做出如下假设。
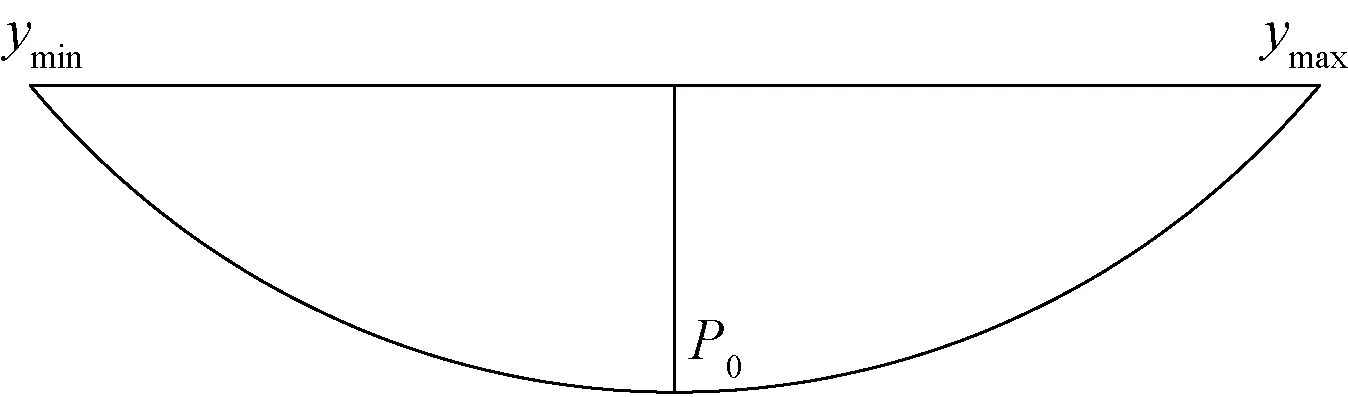
图1 滑坡推力横向分布模型Fig.1 Lateral distribution model of landslide thrust
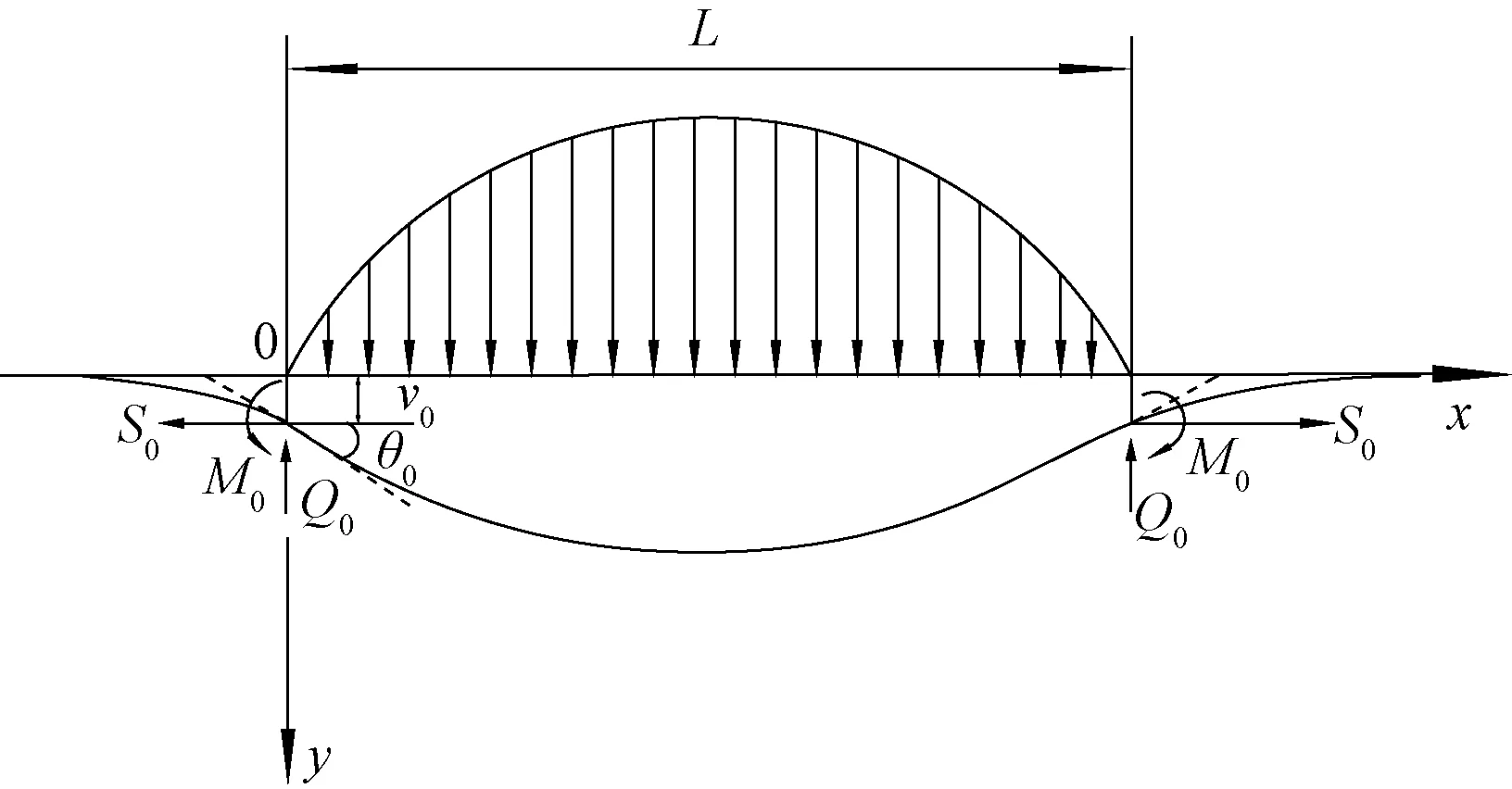
L为滑坡段管道长度,m;M0为管道在x=0、x=L截面的弯矩,N·m;Q0为管道在x=0、x=L截面的剪力,N;S0为滑坡体中管道的当量轴向拉力,N;v0为管道在x=0、x=L处截面的挠度;θ0为管道在x=0、x=L处截面的挠度转角图2 滑坡体内管道受力模型Fig.2 Stress model of landslide pipeline
(1)在滑坡发生时,滑坡推力是导致管道变形的主要作用力,为了简化计算,忽略管道自身及管内介质的重力作用,且忽略下部土体对管道的阻挡作用。
(2)将滑坡体外管道看成小变形的半无限长的梁,且忽略弯曲、拉伸变形的耦合作用影响。
(3)假定土体横向抗力符合Winkler假设,纵向抗力符合双线性假设。
(4)假设管道为无限长的梁,且材质均匀。
(5)假定土壤物性均匀分布,管道受力变形时关于中轴对称。
2 管道静力学分析
管道在温差、内压及下滑土体作用力的联合作用下发生变形,产生的当量轴力的拉压性质并不能确定,需要分情况来对滑坡段管道的受力情况进行讨论。
2.1 S0为拉力时的解
如图2所示,建立坐标系x-y,根据滑坡推力横向分布模型,可得到滑坡推力的分布曲线方程及x=0截面处剪力为
(2)
(3)
根据对称性和连续性条件,对滑坡段管道L,弯曲微分方程为

(4)
式(4)中:E为管材弹性模量,Pa;I为管道的截面惯性矩,m4;y为管道的挠度,m;S0的计算公式[13]为
(5)
式(5)中:N0为管道在x=0、x=L截面的轴力,N;p为管道受到的内压,Pa;d为管道的内径,m。
非齐次方程的特解为
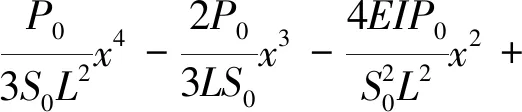
(6)
非齐次方程的通解为
(7)
则可得

(8)
根据对称性及边界条件可得
(9)
得
(10)
对滑坡体外管道进行分析可得,在x=0截面的挠度v0、转角θ0[14]分别为
(11)
式(11)中:系数k和β的计算公式为
(12)
式(12)中:cy0为滑坡体外土体的横向阻力系数,N/m3;D为管道的外径,m。
根据变形协调条件,即滑坡体内外管道截面在x=0处转角相等,得
M0=
(13)
将参数C1、C2、M0代入式(8)、式(9)即可得管道转角和挠度的表达式。
弯矩为

(14)
剪力为
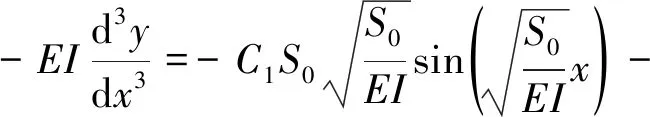
(15)
管道在x=L/2处的挠度为
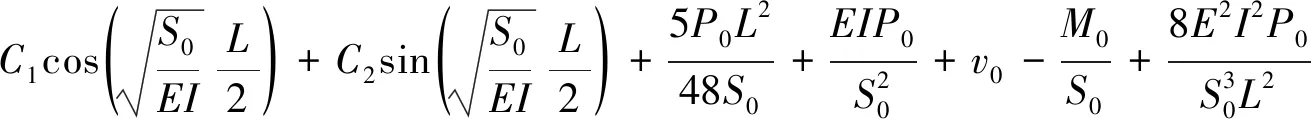
(16)
2.2 S0为压力时的解
当S0为压力时,滑坡段管道的弯曲微分方程为
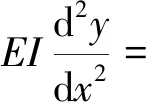
(17)
同理可解得滑坡段管道的挠度为
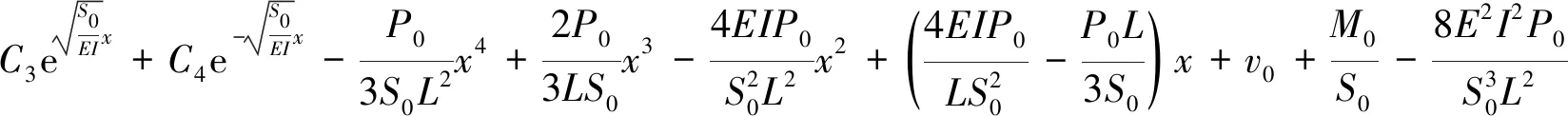
(18)
其中:
(19)
M0=
(20)
弯矩为

(21)
剪力为
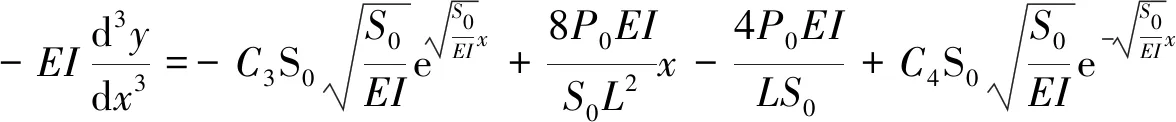
(22)
管道在x=L/2处的挠度为

(23)
2.3 纵向位移计算
以上计算只能导出挠度f和当量轴力S0之间的一个方程,所以还需要利用滑坡体内外管道纵向位移的连续性再导出一个方程来求解[15]。
(24)
式(24)中:
(25)
式(25)中:F为管道的金属截面积,m2;α为管道的线性膨胀系数,m/(m· ℃);ΔT为管道的操作温度与敷设温度之差,℃;μ为管材的泊松比;σh为内压引起的管道环向应力,Pa;D为管道的外径,m;cx0为滑坡体外土壤的切(纵)向阻力综合系数,N/m3;tf为滑坡体外土壤的极限抗剪强度,kPa。
2.4 S0拉压性质的判定
S0拉压性质的确定可以通过S0=0时解间接的导出其判别式。
当S0=0时,滑坡体内管道的挠曲线方程为

(26)
管道在x=L/2处的挠度为
(27)
式(27)中:M0的计算公式为
(28)
在S0=0时,滑坡体内管道由于推力、内压、温差、轴力作用引起的相对纵向位移U1计算公式为
(29)
滑坡体外管道在x=0、x=L截面的相对纵向位移U2的计算公式为
(30)
由此可以得到S0拉压性质的判据为:①当U1>U2时,S0为拉力;②当U1=U2时,S0=0;③当U1 在管道强度的设计计算中,壁厚可由环向应力确定,内压、温差及管道弯矩作用产生的组合应力可利用强度理论建立的材料强度条件校核管道应力的安全状态。 油气管道是薄壁,因此,一般可忽略径向应力,只考虑环向应力和轴向应力,其计算公式如下: 轴向应力计算公式为 (31) 环向应力计算公式为 (32) 式中:N为管道轴力,N;M为管道弯矩,N·m;F为管道截面面积,m2;W为管道截面抗弯模量,m3,计算公式为 (33) Tresca屈服准则,即最大剪应力屈服准则,因其计算简单,稍偏于安全,是大多数油气管道工程设计规范采用的强度理论,其强度条件为 (34) 式(34)中:σeq为当量应力,Pa;σ1、σ3为第一、第三主应力,Pa;[σ]为许用应力,Pa。 根据《输油管道工程设计规范》(GB 50253—2014)5.2.1输油管道直管段的许用应力的规定有 [σ]=Kφσs (35) 式(35)中:K为设计系数;φ为焊缝系数;σs为钢管最低屈服强度,Pa。 以忠-武线沿线某滑坡为例[6],评价管道安全性。 该滑坡朝向北东,坡度为32°,坡顶为平缓小山包;斜坡的地层为志留系龙马溪组黄绿色页岩,倾向南东,倾角25°~55°,基岩强风化,表层覆盖3~5 m 残坡积碎块石土。滑坡面积100 m2,滑体厚度2~4 m,宽度约40 m,滑动方向40°。 管材采用X65型钢,规格φ711 mm×7.9 mm,弹性模量E=207 GPa,泊松比μ=0.3,线膨胀系数α=1.2×10-5m/(m·℃),最低屈服极限σs=450 MPa,内压p=4.0 MPa;温差ΔT=-10 ℃;纵向阻力综合系数cx0=5.88 N/cm3,横向阻力综合系数cy0=2.45 N/cm3,滑坡体外土体的极限抗剪强度tf=24.6 kPa;主滑断面处剩余下滑力P0=6.525 kN/m。 假设滑坡下部土体滑动,采用本文算法,利用牛顿迭代法或作图法计算管道位移及内力,计算结果如表1及图3、图4所示。 由图3(a)知,滑坡周界至滑坡体中部,管道挠度先变大后变小;由图3(b)知,滑坡周界至滑坡体中部,管道弯矩先减小后增大,且管道两端表现为正弯,至滑坡体中部管道逐渐转变为负弯,滑坡周界处管道弯矩最大,易发生弯曲破坏;由图3(c)知,滑坡周界至滑坡体中部,管道剪力逐渐减小,管道两端剪力最大。 由图4(a)知,滑坡周界至滑坡体中部,管道轴向应力逐渐减小,且均变现为拉应力;由图4(b)知,σeq的值先减小后增大,σeq,max=224.9 MPa<[σ]=0.5×1.0×450=225.0 MPa,管道处于安全状态,但已经接近极限。考虑管道实际受力情况,管道下侧土体对管道有支撑作用,因此,实际受力情况要比计算的好。在滑坡体中部及滑坡周界处,管道σeq应力达到极值点,是极易发生破坏的位置。 表1 管道挠度及内力计算结果Table 1 Pipe deflection and internal force calculation results 图3 管道挠度、弯矩、剪力曲线Fig.3 The curves of pipe deflection,bending moment and shear 图4 管道应力与轴向长度关系曲线Fig.4 Relation curve of pipe stress and axial length 由图3、图4知,管道挠度两端较小,中部较大;轴向应力也是中间较小,两端较大;当量应力两端较大,是较容易破坏的位置;与文献[6]中解析方法所得到的结果基本一致。管道当量应力为224.9 MPa,与文献[6]中所得到的207.4 MPa,211.3 MPa相比,较为接近,安全性评价相对保守,说明精度可以满足工程要求。 图5 边坡及管道模型图Fig.5 Slope and pipeline model diagram 根据忠-武线沿线某滑坡基本特征,基于ABAQUS软件,建立图5所示模型,z轴方向上,山体长AI=70 m,滑土体长HG=40 m,与斜坡两端的距离均为15 m,最深位置为4 m;y轴方向上,山体前后高度分别为AF=5 m、BC=45 m;x轴方向上,斜坡前后距离AB=80 m,上下两端平坦部分EF、DC均为10 m;管道埋深2 m。 土体采用Mohr-Coulomb模型,其中滑土体弹性模量E=0.035 GPa,容重γ=21 kN/m2,泊松比μ=0.35,摩擦角φ=27°,黏聚力c=18 kPa;滑床弹性模量E=12 GPa,容重γ=25 kN/m2,泊松比μ=0.32;管道采用线弹性模型,其弹性模量E=207 GPa,泊松比μ=0.3,密度ρ=7.85×103kg/m2;土体以及管道网格划分采用C3D8R单元;管道的两端和坡体底部为固支,左右的两端面除竖直方向外施加全部约束,两个断面约束水平方向位移;整个模型施加重力荷载,管道内部压强为4 MPa。 计算结果如图6、图7所示,滑坡发生变形时,管道主要受到滑坡推力的作用,管道的挠度和Mises应力都关于y轴对称。滑坡周界处管道挠度最小,向滑坡正中位置挠度逐渐增大;滑坡周界处管道Mises应力最大,向滑坡中间位置先减小后增大,在中间段管道Mises应力变化较平缓,可知滑坡周界附近管道容易受到破坏。 图6 滑坡位移云图Fig.6 Landslide deformation diagram 图7 管道位移内力图Fig.7 Pipeline displacement internal force diagram 对比图3(a)和图7(a)、图7(b)可以看出,在滑坡作用下的管道挠度变化趋势相同,滑坡周界处挠度最小,向滑坡中间挠度逐渐变大,两者比较接近,说明采用本文算法计算横向滑坡作用下管道变形还是比较合理的,滑坡体中部挠度最大,易发生拉压破坏;对比图3(c)、图3(d)和图7(c)、图7(d)可知,从理论计算与数值模拟整体看,都显示滑坡周界附近管道受力最大,管体会最先屈服,最容易发生破坏;图8中B与B′两处受到滑坡推力的作用,产生压应力,而滑坡周界处土体变形不明显,A与A′两处主要受到管道中部变形产生的拉应力,因此,选择管道的监测点时,在A与A′选择管道应变监测,B与B′选择管土压力监测。 图8 管道变形图Fig.8 Pipeline deformation diagram 根据以上推导分析,可得出如下结论。 (1)基于Winkler弹性地基梁模型和滑坡推力横向分布模型,考虑温差、内压以及推力等因素产生的当量轴力的作用,建立横向滑坡作用下埋地管道受力变形的力学模型,通过求解管道变形的弯曲微分方程,得到管道位移、转角、弯矩以及剪力的计算表达式。 (2)结合工程案例,采用本文算法,编程计算得到管道挠度、弯矩、剪力、轴向应力、当量应力曲线,验证了本文算法的合理性;通过分析知,滑坡周界及滑坡体中部管道最容易发生破坏。在计算过程中,阻力综合系数的选用对计算精度至关重要,因此,在实际工程中应加强勘测,正确选用参数。 (3)基于ABAQUS软件,建立数值模拟模型,对滑坡作用下管道受力变形进行了模拟计算,得到了管道位移与Mises应力云图,并与理论计算结果进行了对比,管道挠度变化趋势相同,滑坡周界附近以及滑坡中部管道最容易发生破坏。 (4)在管道埋设过程中尽量绕避潜在滑坡区,若不可绕避,则需要对斜坡以及管道加强监测,并避免在滑坡周界以及滑坡体中间位置设置接头,以免应力集中造成的管体加速破坏。3 管道强度校核
4 工程实例计算分析
4.1 滑坡基本特征
4.2 计算参数
4.3 计算结果分析

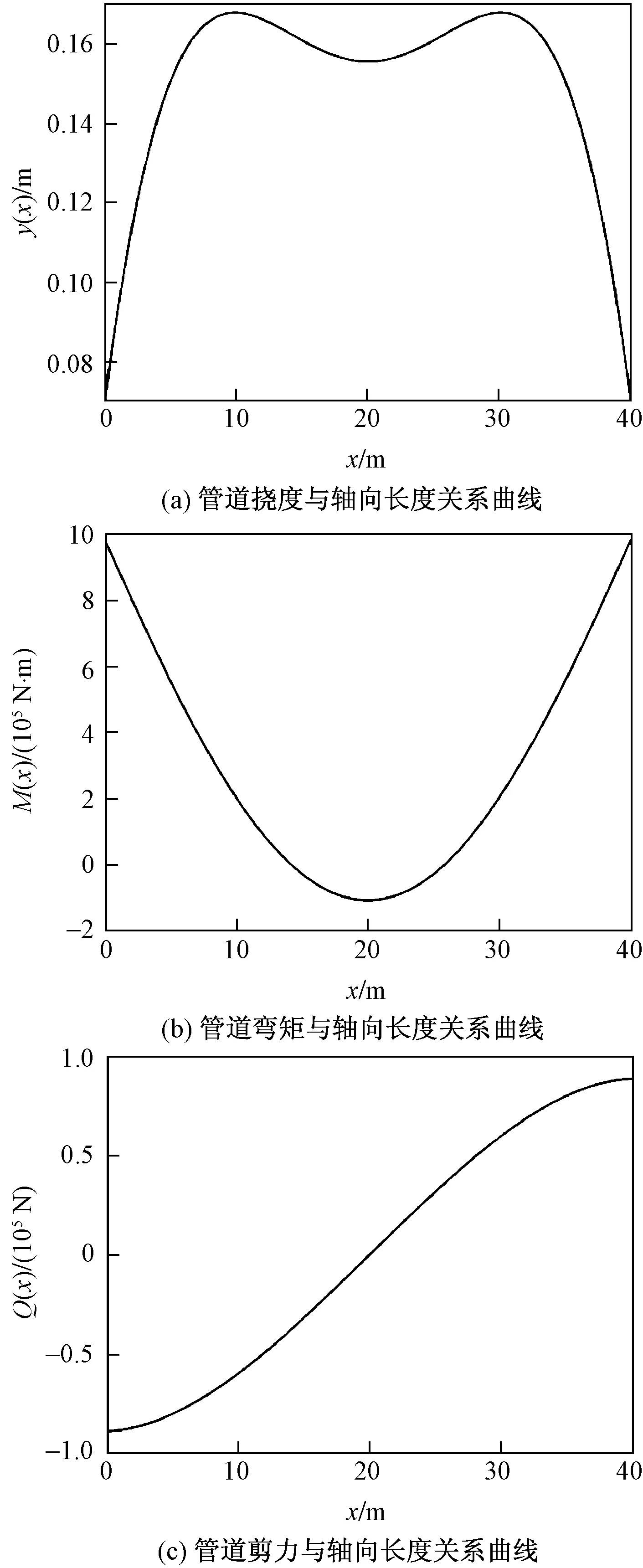

5 数值模拟验证
5.1 模型建立
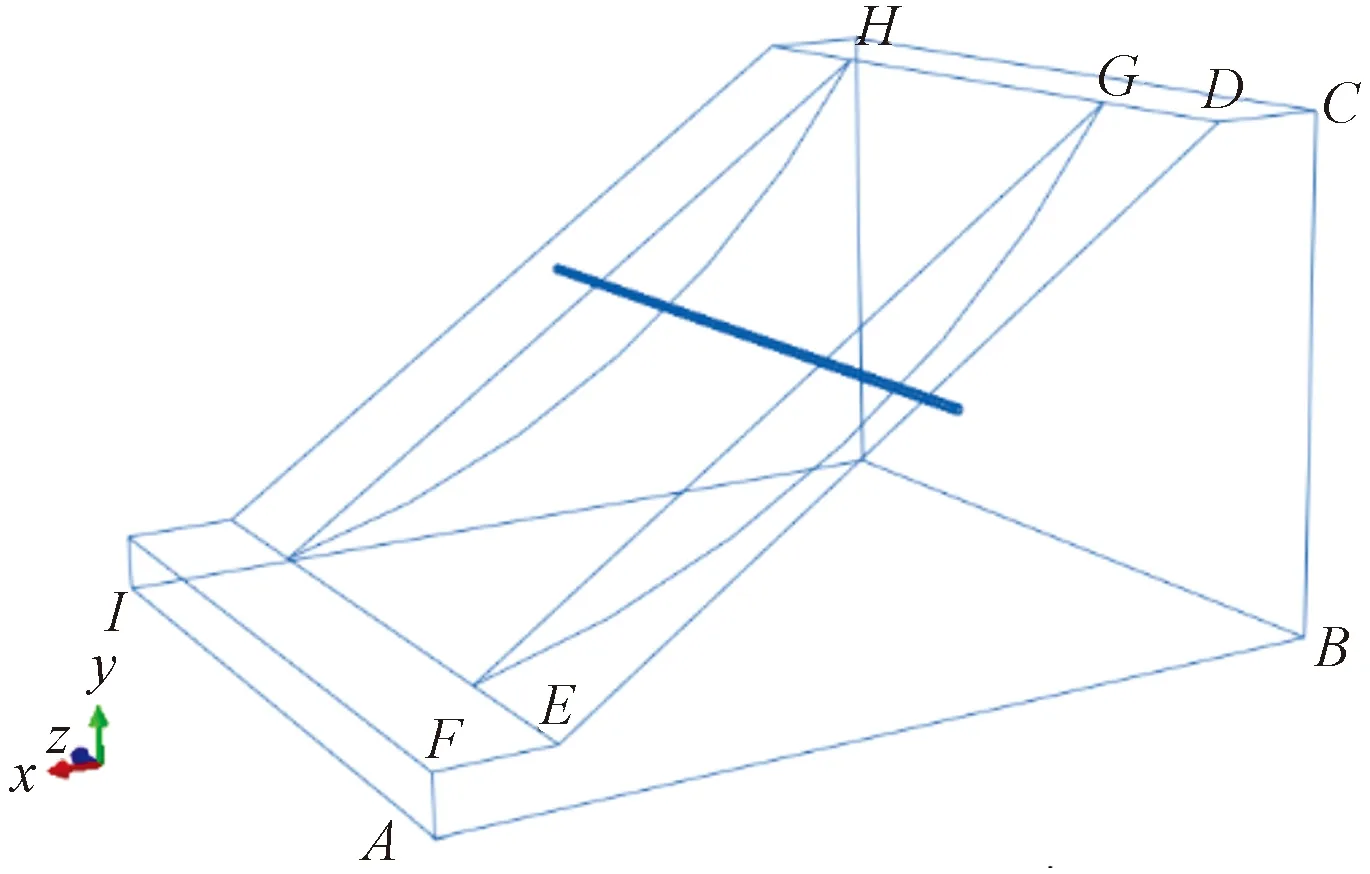
5.2 模拟结果


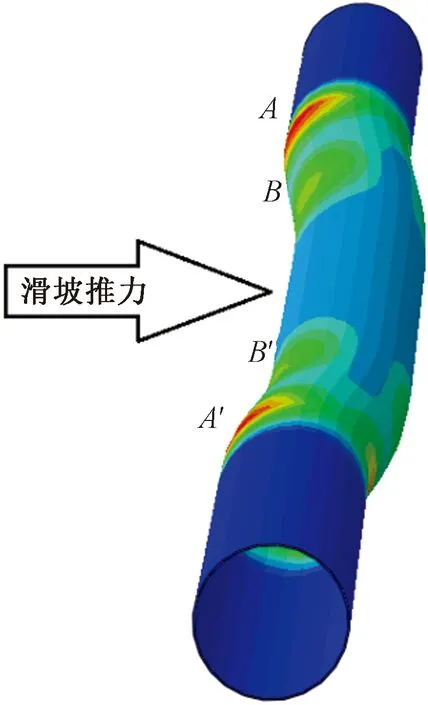
5.3 对比分析
6 结论

