例谈高中数学解题教学的原则

广东省河源市源城区东埔中学(517000)廖新红

美籍数学教育家波利亚有一句脍炙人口的名言:“掌握数学就是意味着善于解题”.对于学生而言,解题是学好数学的重要途径;对于教师来说,解题教学是数学教学的重要组成部分.通过听课学习及研讨,我们发现,不少高中学校的数学解题教学存在以下突出问题:

(1)题目的选择过难,超出了学生的知识现状.

(2)有些老师给出题目后,留给学生尝试求解的时间严重不足.

(3)有些教师往往只讲解题过程,忽略了向学生介绍自己的思路以及解题的程序.

(4)解题教学后反思不够.

实际上,高中数学教师在解题教学中应当遵循一些基本原则,才能使学生在数学解题课堂上学得轻松明了,不至于云山雾罩、似懂非懂.下面,本人通过例题探索高中数学解题教学的一些基本原则.

1 探索高中数学解题教学的基本原则

1.1 选题优化原则

选题优化原则,是指课堂教学所选取的例题、练习题和作业题,应有启发性,并能层层递进,能突出通性通法,利于强化重点、突破难点、矫正误点,从而符合优质选题要求的解题教学原则.

例1(2018年高考天津卷理科第15 题)在ΔABC中,内角A,B,C所对的边分别为a,b,c,已知bsinA=.

(1)求角B的大小;

(2)设a=2,c=3,求b和sin(2A−B)的值.

这道例题考查正、余弦定理,两角差的正、余弦公式及二倍角的正、余弦公式这些重要知识点.这道例题的选择,体现了高考真题的综合训练价值,能突出解三角形中常见的边化为角的转化与化归的通性通法,有利于强化解三角形一章中的重点内容“正弦定理与余弦定理”,更能突破“解三角形与三角恒等变换有机综合”的难点,同时还能矫正一个“由就直接得出”的误点.选择这道题作为高三复习课的例题,符合选题优化原则,有利于提高解题教学的有效性.

选题优化原则,是高中数学解题教学的首要原则.在数学教学中,“教什么”远比“怎么教”和“教如何”更重要.

1.2 尝试性原则

尝试性原则,是指在课堂解题教学中,在老师讲解一道题之前,提前让学生先尝试求解几分钟(也可提前一天让学生先做)获得解题感知或解题经验,这种先练后讲,练在讲之前的解题教学原则称为尝试性原则.

尝试性原则,能增加学生的基本活动经验,可防止教学的突兀性,提升解题教学效果.

1.3 暴露性原则

暴露性原则,是指在课堂解题教学中,教师要向学生主动暴露自己的解题思路且自然而清晰,从而引导学生学会思考的解题教学原则.

例2(2018年辽宁高三模拟理科第21 题)函数f(x)=xex−lnx−ax.

(1)若函数y=f(x)在点(1,f(1))处的切线与直线y=2(e−1)(x−1)平行,求实数a的值;

(2)若函数y=f(x)在[1,+∞)上单调递增,求实数a的取值范围;

(3)在(1)的条件下,求f(x)的最小值.

暴露性原则,有利于将教师的所思、思维受阻时的解决途径详细地为学生呈现出来.教师在解题教学中遵循暴露性原则,有利于教会学生思考,比单纯的呈现解题过程更有利于发展学生的思维.

1.4 程序性原则

程序性原则,是指课堂解题教学中,要向学生概括(或由学生概括)解某一道题的大致步骤的解题教学原则.

例3(2019年高考全国I 卷理科第18 题)如图1,直四棱柱ABCD−A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

图1

(1)证明:MN//平面C1DE;

(2)求二面角A−MA1−N的正弦值.

老师在讲解这道题的过程中,应向学生概括出(或由学生概括出)解答本题的大致步骤.

比如完成本题第一问分三步进行:第一步连接B1C与ME,由三角形的中位线定理证出ME//B1C;第二步由及点N为A1D的中点证出于是得出四边形MEDN为平行四边形,随后证出MN//ED,第三步由直线与平面平行的判定定理证出MN// 平面C1DE.

完成本题第二问分四步进行:第一步由底面ABCD为菱形及∠BAD=60°推出ΔABD为等边三角形,再由点E为BC的中点及ΔCBD为等边三角形推出∠BDE=30°,从而AD⊥DE,再由直棱柱的定义得出D1D⊥底面ABCD,从而D1D⊥AD,D1D⊥DE,这样为建立空间直角坐标系创造了完备的条件;第二步以点D为坐标原点,以的方向分别为x轴,y轴,z轴的正方向,建立如图2 所示的空间直角坐标系D−xyz,然后写出四个点A,M,A1,N的坐标及向量的坐标;第三步分别求出平面A1MA和平面A1MN的法向量;第四步利用法向量法求出二面角A−MA1−N的余弦值和正弦值.

图2

在数学解题教学中,教师经常运用程序性原则,能逐步提升学生的归纳概括能力,培育学生数学解题的逻辑性,从而循序渐进地提升学生数学抽象、逻辑推理等数学核心素养.

1.5 直观性原则

直观性原则,是指课堂解题教学中,教师应尽可能借助信息技术或直观操作演示或画图形将抽象的知识,直观化地呈现在学生面前的解题教学原则.

例4(2019年高考全国I 卷文科第20 题)已知函数f(x)=2 sinx−xcosx−x,f′(x)为f(x)的导数.

(1)证明:f′(x)在区间(0,π)存在唯一零点;

图3

这时可作出f′(x)的准确图像,如图4,加以验证.

图4

(2)因为当x ∈[0,π]时,f(x)≥ax,且f(π)=0,所以a≤0.由(1)知f′(x)在(0,π)内只有一个零点.设此零点为x0,则当x ∈(0,x0)时,f′(x)>0;当x ∈(x0,π)时,f′(x)<0.所以f(x)在(0,x0)上单调递增,在(x0,π)上单调递减.又f(0)=0,f(π)=0.

这时老师可以结合上述信息画出函数f(x)的大致图像,如图5.结合图像容易得出当x ∈[0,π]时,f(x)≥0 的结论.又当a≤0,x ∈[0,π]时,ax≤0,能使f(x)≥ax.

图5

同时画出y=f(x)及y=ax的大致图像,如图6.故a的取值范围是(−∞,0].

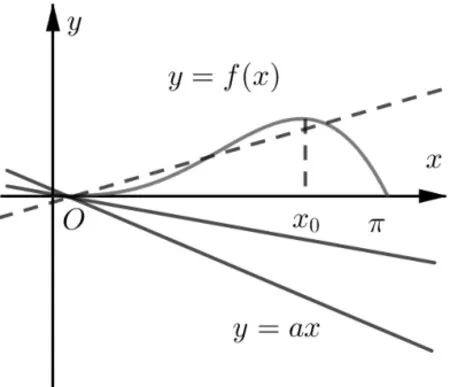
图6

在数学解题教学中,教师遵循直观性原则,能将抽象的数学问题直观化,促进了信息技术与数学教学的深度融合,降低了学生听课的难度,提升了学生直观想象的数学核心素养,很好的体现了数形结合的数学思想方法.

1.6 解后反思原则

解后反思原则,是指课堂解题教学中,老师在解完一道题后要及时地总结或反思本题考查的基础知识、基本思想方法、基本技巧等,通过总结解题经验对后续解题起到借鉴作用的解题教学原则.

例5(2018年高考全国I 卷文科第21 题)已知函数f(x)=aex−lnx−1.

(1)设x=2 是f(x)的极值点,求a,并求f(x)的单调区间;

本题主要考查利用导数研究函数的单调性、极值、最值、不等式恒成立问题.本题解答后要注意带领学生反思,防止“入宝山而空返”,错失提升良机.可反思以下四点:

(1)若x=x0是函数f(x)的极值点,那么____.对于可导函数y=f(x),“f′(a)=0”是“函数y=f(x)在点x=a处取得极值”的____条件.

(2)用导数法求函数的单调区间的步骤.(不要忽略函数的定义域喔!)

(3)证明函数不等式f(x)≥(或≤)g(x)的方法.

(4)当a≥0 时,讨论函数f(x)=(1+ax2)ex−1 的单调性.

当然,解后反思不仅包括解后带领学生反思,而且包括解后教师在教学方法、教学细节等方面的自我反思.

2 结束语

以上结合实例探索了高中数学解题教学的六个基本原则,由于能力所限,文中难免出现错误,恳请专家批评指正.另外,高中数学解题教学可能还有其它的一些原则,恳请专家予以补充.