海上风机嵌岩桩水平承载特性有限元分析

张浦阳， 董宏季， 乐丛欢， 丁红岩

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072； 2.天津大学 建筑工程学院，天津 300072)

风能是一种清洁能源，随着化石能源的逐渐枯竭，风能的开发利用逐渐受到世界各国的重视。我国沿海地带风资源丰富，海上风机逐渐发展[1]。福建海域地质条件复杂，多为岩基海床，其覆盖层厚度及组成变化大，基岩埋深及风化程度变化大。目前国内已建和在建的采用单桩基础的海上风机基本都位于软基海床，单桩基础基岩海床的工程经验较少。分析单桩水平承载特性的研究方法主要有试验法、理论分析方法、有限元法。其中试验分为原型试验和小模型试验，原型试验耗资较大，而且目前国内外已竣工的海上嵌岩桩工程较少，缺乏相关数据；小模型试验难以反应原型[2]。理论分析法中具有代表性的p-y曲线法[3]，是目前应用最广泛的计算横向荷载作用下桩体荷载传递特性的方法，p-y曲线法是由小直径桩试验得到的，其能否用于大直径桩基础有待研究[4]，且p-y曲线公式与土的参数密切相关，很多学者对其进行了修正，但都只是针对单一土质，其普适性较差[5-6]。有限元法是随着计算机发展而生的一种现代化方法[7-9]。本文通过建立三维有限元模型，对福建海域海上风机单桩嵌岩基础水平承载特性开展研究，希望通过研究为后续福建海域风电场单桩基础设计提供理论指导。

1 有限元模型

海上风机单桩基础是一种超大直径钢管桩结构，直径通常在5～8 m，其桩土相互作用是一个三维的相互作用模式，其水平向相互作用主要分为[10]：1)桩侧与土之间的水平抗力；2)桩侧与岩石之间的水平抗力；3)桩底与岩石之间的摩擦力。

本文计算中桩径D=6.5 m,为更直观地研究桩身传力规律，桩身壁厚沿长度方向设为定值，厚度为0.01D[11]。泥面以上桩自由端30 m，其中水面下长度15 m。底部嵌入弱风化岩层中。桩为植入式基础，内部无土。

根据福建某海域地质条件，平均水深设为15 m，有限元模型中岩层上部土体简化为单一土层，土体宽度80 m，大于10倍桩径，土体总高度65 m，其中表层砂层厚度13 m，下部为弱风化岩层。本文计算的所有工况中，桩底距岩石底部距离均大于5D。土体侧边界约束水平位移和竖向转角，土体底部边界6个自由度全部约束。土质参数见表1，泥质粉细砂(下文中简称砂土)采用摩尔-库伦本构模型[12]，岩石设为线弹性材料[13]。桩与砂土为主从摩擦接触，桩身外表面为主面，摩擦系数μ=tan(0.75Φ)[14]。因目前还未有已经应用的海上嵌岩桩的施工工艺和方法，桩与岩石的接触形式尚不明确，认为与桩-砂土接触形式相同，桩外侧为主面，设摩擦系数0.6。有限元模型图见图1，水下桩身材料采用浮容重。

表1 土质参数

图1 桩-土有限元模型

风机运行过程中收到风浪流荷载的共同作用，水平荷载是影响桩身弯曲变形的主导因素。以桩顶水平位移S=0.05D为控制标准[15]，作为桩顶水平变形的极限状态，对应的桩顶荷载P即为桩的水平承载力。通过改变嵌岩深度，计算嵌岩深度对桩承载力的影响。

2 嵌岩深度的影响

图2为承载力随嵌岩深度的变化情况。嵌岩深度2 m时的承载力约为未嵌岩工况的4倍；嵌岩深度0～6 m内，承载力随嵌岩深度近似线性增加；继续增加嵌岩深度，承载力增长趋势逐渐变小；嵌岩深度达到12 m后，继续增加嵌岩深度，承载力不再提高。

图2 承载力随嵌岩深度的变化

图3为不同嵌岩深度下桩的P-S曲线图。桩底部未嵌入岩层中，桩顶水平反力随桩顶位移增大而增大，最后逐渐趋于平缓；嵌入岩石中的桩P-S曲线接近直线，表明桩身、桩周土体以及岩石均未发生破坏；嵌岩深度12～16 m的3条P-S曲线在图中接近重合，深度由12 m增加到14 m时，承载力增大了5‰。

桩基础在保证承载力满足要求的同时也要保证自身以及岩石的强度，桩身以及岩石最大应力随嵌岩深度变化见图4、图5。未嵌岩情况下，桩身应力最大处位于桩底，因为此时桩未嵌入岩层，砂土层能够提供的土抗力有限，随着桩顶荷载增大，桩整体发生转动，向前倾覆，桩身自重以及外荷载产生的内力集中在桩前趾，导致前趾处应力较大；嵌岩深度2～6 m内，桩身应力最大处位于桩底后趾；嵌岩深度超过一倍桩径后，桩身应力最大处位于桩前侧泥面下12 m，即岩-土交界面上方1 m，再继续增加嵌岩深度，其位置不再变化，数值上变化较小，桩身应力达到250 MPa,继续加载桩身可能破坏。

图4 桩身最大应力及位置随嵌岩深度变化

图5 岩石最大应力随嵌岩深度变化

岩石应力最大处始终位于桩前侧岩石表层上，在数值上远小于岩石抗压强度。所以可以认为桩身先于岩石破坏，桩破坏时，岩石还处于弹性阶段。

桩基础的破坏模式主要分为压曲破坏、剪切破坏和刺入破坏。由于弱风化层的岩石强度较大，刺入破坏暂不考虑。压曲破坏和剪切破坏与桩身弯矩、剪力分布密切相关，桩身横截面弯矩和剪力为：

(1)

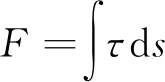
(2)

式中：σz为横截面上的拉压应力；τ为横截面上的剪应力。

在有限元中通过对桩身横截面应力积分得出在桩顶位移0.05D时弯矩和剪力沿桩身分布，其随嵌岩深度的变化规律见图6、图7。

弯矩变化规律:1)砂土层：桩身弯矩从砂土层表面向下至岩-土交界面处逐渐增大，随嵌岩深度增大，弯矩沿桩身向下增长趋势逐渐接近线性；2)岩石层：从岩-土交界面向下直至桩底弯矩随深度增加线性减小；随着嵌岩深度增加，桩底弯矩逐渐变小，同时靠近桩底处弯矩随深度变化趋势变小。

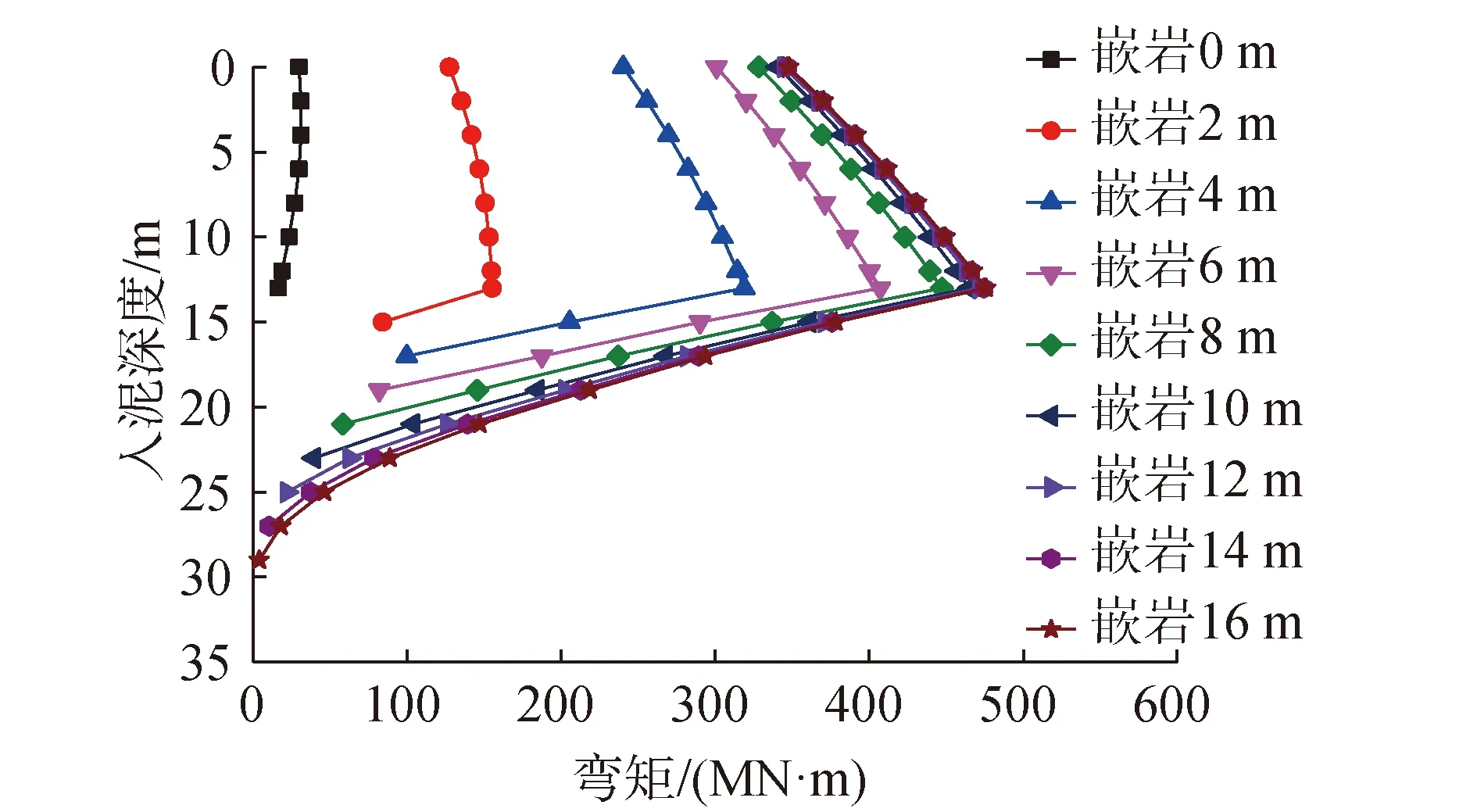
图6 桩身弯矩沿深度变化

剪力变化规律：桩底未嵌入岩石情况下，桩身剪力方向在中上部方向发生改变，数值上沿深度方向线性减小；桩底嵌入岩石后，桩身横截面剪力由泥面处至桩底逐渐降低，方向未发生变化，至岩-土交界面处，剪力方向改变，嵌岩段整体剪力方向与砂土层剪力方向相反。剪力最大截面处位于嵌岩 4 m处，最大值45 MN,截面上平均剪应力远小于钢材的抗剪强度。

桩身应力最大处位于岩-土交界面上部1 m处，该位置桩身弯矩较大，剪力很小，故认为嵌岩桩是压曲破坏模式。

海上风机是一种高耸结构，倾斜率是保证其正常工作运行的重要指标。桩身倾斜率过大，桩顶上部的塔筒和风机机头会产生较大的偏心荷载，严重影响基础稳定。图8为桩顶和泥面处倾斜率变化图。泥面处倾斜率随嵌岩深度增加逐渐降低，最终稳定在6‰。嵌岩深度小于1倍桩径时，桩顶倾斜率随嵌岩深度增加而减小，超过1倍桩径后，桩顶倾斜率缓慢增加，最终趋于稳定，最终倾斜率小于10‰。

通过改变嵌岩深度，从承载力、桩身内力分布、桩身变形判断嵌岩桩的合理嵌岩深度，认为嵌岩2D左右为合理的嵌岩深度。为验证此结论，建立直径7.5 m，壁厚75 mm的桩进行对比，其余参数不变，对桩顶施加水平位移0.05D，承载力结果如图9所示，图中变化率为嵌岩深度每增加1 m的承载力的变化率，嵌岩深度超过2D后，承载力基本不再变化。

图8 桩顶和泥面处桩身倾斜率随嵌岩深度的变化

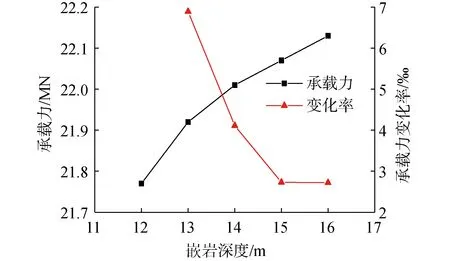
图9 承载力随嵌岩深度变化

3 分级荷载作用下桩的承载特性分析

为研究桩身传力规律以及桩-土作用形式，采用第2节中嵌岩12 m、直径6.5 m的工况，对其桩顶分级加载，取桩顶位移0.05D对应的水平荷载作为极限荷载，荷载值H=11.5 MN,分5级加载。

3.1 桩身变形

泥面下桩身变形见图10，砂土层桩身弯曲变形，绕嵌岩位置处发生转动，各深度处桩身水平变形随桩顶荷载增大接近线性变化，与图3中P-S曲线为线性相一致；嵌岩0～4 m内桩身水平变形很小。桩顶及泥面处转角变化见图11，桩顶和泥面处转角随荷载增大线性增大，桩顶倾斜率约为泥面处倾斜率的1.6倍，表明泥面上桩自由端产生弯曲变形。

3.2 桩身内力分布

桩身弯矩分布如图12，随桩顶荷载增大，弯矩分布规律不变，在数值上变化明显：在砂土层，弯矩随桩的埋深增大线性增加，在岩石表面达到峰值；弯矩在嵌岩深度1D范围内线性减小，接近桩底处曲线弯曲，减小趋势逐渐变缓，桩底弯矩不为0。随着荷载等级增大，桩身各截面弯矩值呈线性增长，弯矩最大处始终位于岩-土交界面上。

图10 桩身水平变形

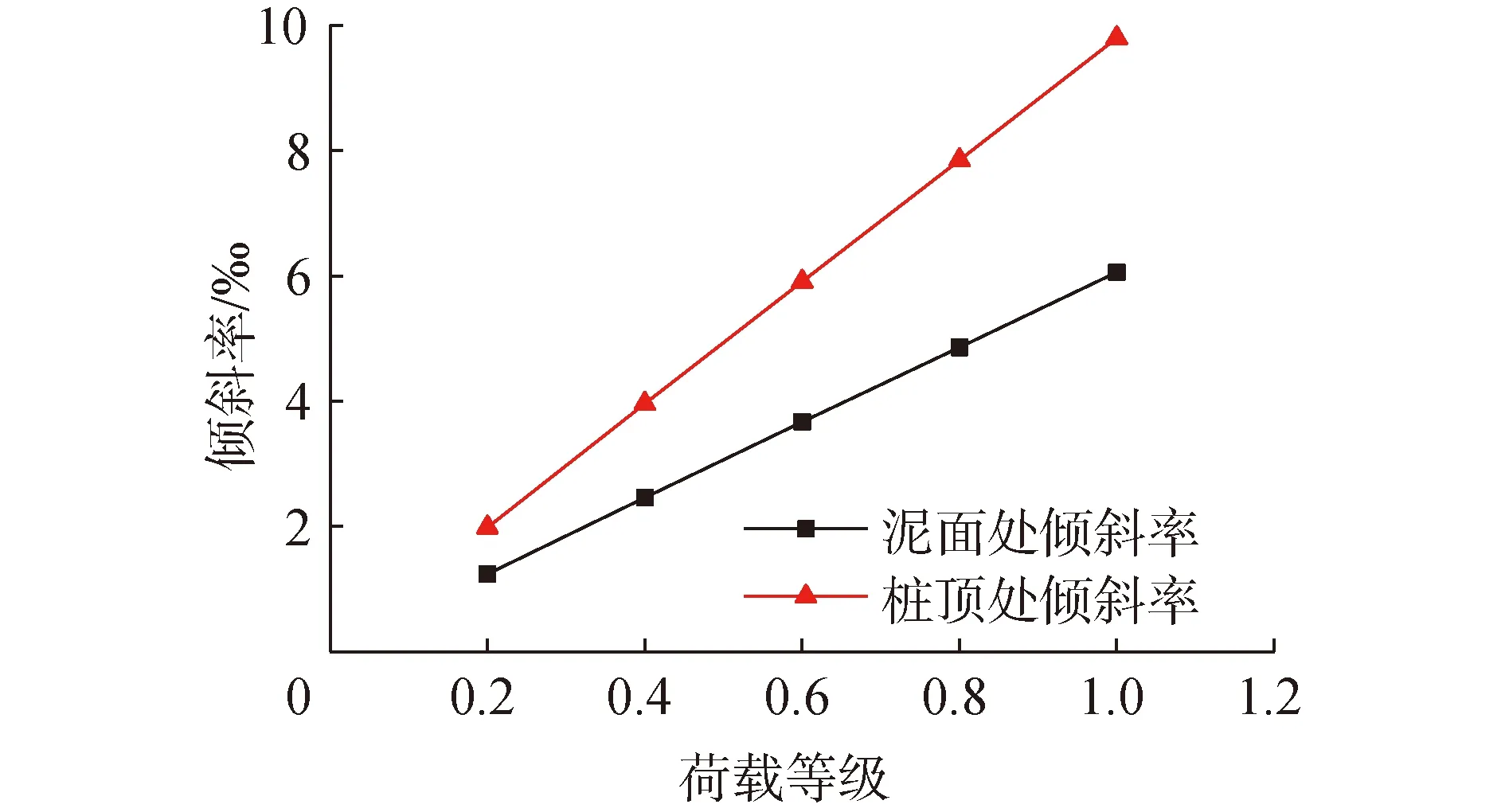
图11 桩顶及泥面处桩身倾斜率变化

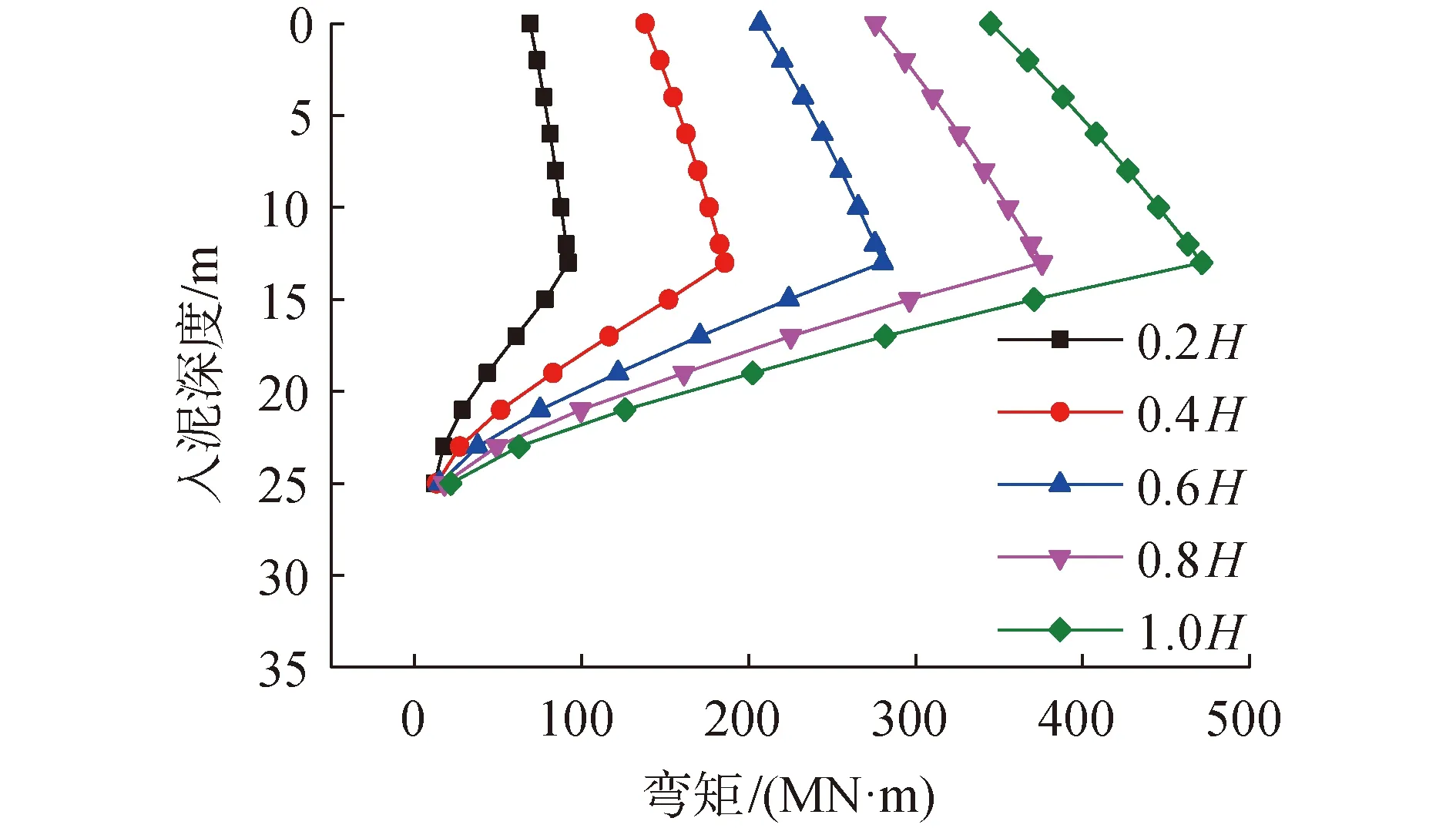
图12 桩身弯矩分布

桩身横截面水平剪力分布如图13，水平荷载下桩身剪力沿深度呈现以下规律：砂土层处剪力值从泥面处向下线性减小，数值上变化较小，剪力方向未改变；在岩-土交界面处剪力方向发生变化，且在数值上突然增大，在嵌岩4 m处达到峰值；剪力达到峰值后，从峰值处至桩底迅速减小，桩底剪力数值上约为泥面处的一半，方向相反。随着桩顶荷载增加，桩身横截面剪力沿深度分布规律及应力最大处位置始终保持不变。

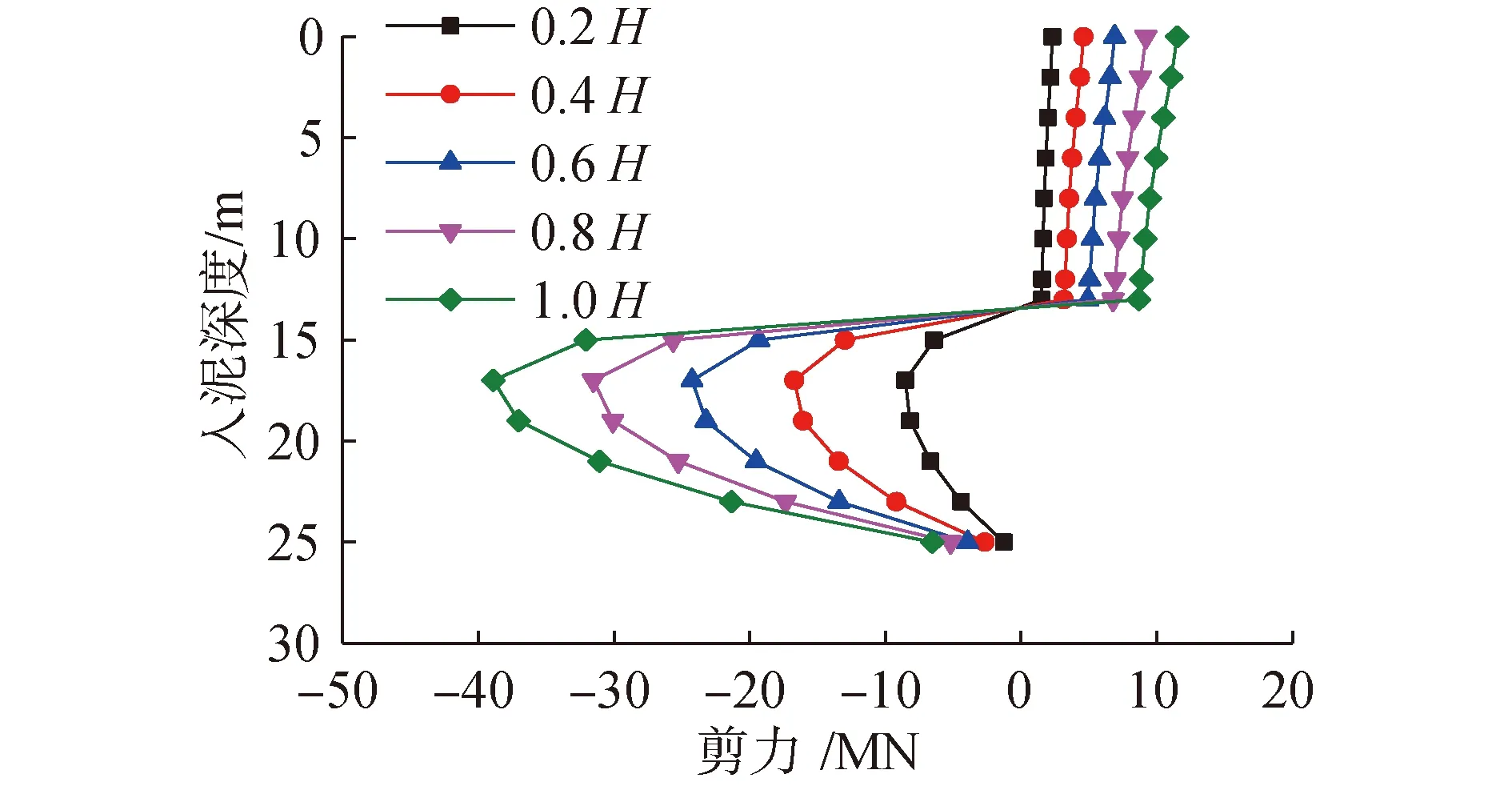
图13 桩身剪力分布

3.3 土抗力分布

桩顶荷载向下传递到泥面以下后，靠地基土抗力维持桩身稳定，桩身单位高度上受到土抗力为：

(3)

沿加载方向上的土抗力为：

(4)

式中：σ为水平向土压力；l为桩横截面外侧与土接触的长度；R为半径。

沿高度上对每米高度上的桩侧土抗力积分，绘制桩侧土抗力沿高度分布图，由于砂土层相比岩石层变化较小，故将砂土层抗力单独显示。

图14为桩后侧土抗力沿深度分布图，其中砂土层土抗力由主动土压力提供，数值上随深度增加线性增大，随着荷载增大，泥面附近砂土与桩开始分离，主动土压力逐渐变为0；桩后侧岩石层土抗力主要由被动土压力提供，距桩底距离越小，数值越大。图15为桩前侧土抗力沿深度分布图，砂土层土抗力由被动土压力提供，随桩顶荷载增加，桩身变形增大，靠近泥面处土体变形最大，土抗力变化最明显，靠近桩底处变形较小，所以抗力变化较小；桩前侧岩石层被动土压力主要集中在嵌岩0～4 m深度处。图16为桩侧土抗力沿深度分布图，砂土的土抗力在数值上远小于岩石的土抗力，岩石层的被动土压力对桩身稳定起主要作用。

图14 桩后侧土抗力沿深度分布

图15 桩前侧土抗力沿深度分布

从图13可看出，桩底剪力大约为外荷载值的一半，除了桩侧土抗力，桩底摩擦力对桩身稳定也起到了一定作用。图17反映了砂土层-岩石层-桩底3部分提供的抗力合力随外荷载增加的变化，其与外荷载比值变化见图18。随着外荷载增大，3部分抗力值均线性增加，岩石层抗力值变化最大，其与外荷载比值有所增大，砂土层土抗力与外荷载比值随外荷载增大而减小，桩底摩擦力与外荷载比值基本保持不变。随着外荷载增大，岩石层的承载作用逐渐提高，砂土层的作用逐渐减弱，桩底摩擦力也起到了一定作用。

图16 土抗力沿深度分布

图17 砂土层-岩石层-桩底抗力变化

图18 砂土层-岩石层-桩底抗力与水平荷载比值变化

4 结论

1)嵌岩桩的水平承载力随嵌岩深度增加而增大，在嵌岩深度达到2D后，继续增加嵌岩深度，承载力基本不再提高，同时桩身变形以及弯矩、剪力的分布也几乎不变，所以2D为嵌岩桩合理的嵌岩深度。

2)嵌岩深度足够时，在分级水平荷载作用下，桩身弯矩、水平剪力沿深度变化趋势不变，数值上随荷载增加呈线性增长。弯矩最大处位于岩-土交界处，桩身横截面水平剪力方向在岩-土交界处发生改变，嵌岩段桩身剪力方向与加载方向相反，在嵌岩深度约0.6D时达到最大。

3)桩身先于岩石达到屈服强度，桩身应力最大值处位于岩-土交接面上约1 m处，桩的破坏模式为压曲破坏。

本文基于以往有限元在软土地基中桩土作用的研究方法，分析了桩在砂-岩石中的水平受荷行为，其中岩石在加载过程中未发生破快，故简化为线弹性材料，未来研究将根据岩性不同，通过物理实验确定更精确的岩石本构模型，以实现具体工程，具体分析。