首部射流对圆柱涡激振荡抑制的实验研究

付国强， 戴绍仕， 孙丽萍， Younis Bassam A.,2

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001；2.加利福尼亚大学戴维斯分校，美国加利福尼亚州 戴维斯市 95616)

模型结构广泛地存在于实际工程领域中。在一定来流的作用下，经常因流分离所致的旋涡脱落使圆柱结构受到周期性的交变力诱发涡激振荡(动)现象，其往往导致结构发生大幅振动，甚至疲劳破坏。如海洋立管、SPAR平台、张力腿平台筋腱等结构的振荡(动)，其直接影响到结构的使用寿命。Sarpkaya[1]、Bearman[2]、Zdravkovich[3]、Williamson[4]等对此问题开展了深入的研究。为了最大程度减小涡激振荡(动)对结构性能带来的影响，在设计阶段就需要采取一定预防措施，如尽量避免结构在稳定流中的约化速度处在可能发生涡激振动的范围、增加结构的有效质量和阻尼以避免其自振频率与涡脱落频率过于接近等，除此之外，通常还需要采用一些抑制装置或手段。

1 旋涡脱落抑制方法

为了减弱或抑制结构的涡激振荡(动)，各国学者纷纷开展针对有效抑制方法的研究。Zdravkovich[5]对旋涡脱落的各种抑制策略进行了总结和分类，分为主动控制方式和被动控制方式2类。主动控制方式需要外加能源驱动，如柱体旋转、抽吸喷吹等；被动控制不需要外加能源，改变结构表面形状或者附加额外装置来影响或抑制旋涡脱落。Blevins[6]将被动抑制方法分为了4类：增加阻尼、避免共振、优化横截面流线型及增加涡抑制装置。螺旋列板[7]、整流罩[8]、分离板[9]、控制杆[10]等装置也被提出用来改变剪切层分离，进而抑制旋涡脱落。

射流方法是一种有效的主动流动控制方法，近年来得到了很多关注。邵传平等[11-12]等通过风洞试验研究了低雷诺数时(2.4×103≤Re≤9.8×103)尾部射流对横向振荡和流向振荡柱体尾流旋涡脱落的影响，发现尾部射流可以消除绝对不稳定性、使负压抽吸使尾流变窄从而抑制柱体振荡。邵传平等[13]数值模拟了低雷诺数(Re=200)时尾部射流对二维圆柱涡脱的抑制，探索了有效的射流速度范围； Feng等[14]采用粒子图像测速(PIV)技术对合成射流(即当流孔的流速周期性变化，保持总质量流量为零时)出口位于圆柱前、后驻点的情况进行了实验研究，发现此方法可以控制圆柱绕流分离，且控制效果与射流出口平均速度的雷诺数有关。Bera等[15]和Tensi等[16]分别采用合成射流方法实验研究了Re在亚临界区时(Re=1.33×105，105)置于不同角度时，合成射流对固定圆柱后缘分离区的影响，发现此方法可以有效推迟流体的分离。Amitay等[17]也采用实验测试的方法研究了合成射流(射流出口为并列狭缝)置于圆周0～180°范围时对圆柱绕流分离的控制，发现了合成射流与自由来流作用会在圆柱表面形成闭合回流区，使得局部流线外移，圆柱表面压力分布得到修正。Skaugset等[18]研究了亚临界区(1.31×104≤Re≤9.18×104)在圆柱周向0°、+120°和-120°沿径向射流的问题，发现了径向水射流模式可以有效地减小涡激振动的幅值和阻力。Lin等[19]采用PIV手段研究了螺旋模式布置的射流对圆柱尾流的影响(Re=1×104)，发现了射流会使得涡量模式发生显著的变形。

由上述的最新研究可知，低雷诺数时尾部射流对圆柱绕流和刚柱振荡的抑制研究已取得了较丰富的研究成果，但较高雷诺数时首部射流对圆柱振荡的影响及量化性的分析还鲜有文章发表。因此，本文利用实验测试的方法研究首部射流在不同射流流量下对单自由度圆柱模型涡激振荡的影响，同时利用功率谱分析的方法分析频谱特性。

2 实验装置与测试

实验在哈尔滨工程大学拖曳水池实验室完成。水池主体尺寸为(长×宽×深)108 m×7 m×3.5 m。拖车最大车速6.5 m/s。

实验所用的射流模型由2部分构成：模型和射流装置。模型是高强度PVC管，外径为160 mm，壁厚为4 mm，相应的长径比为14.375。模型在静水面以下浸没深度(L)为1.1 m。它由2根槽钢和一根光滑的旋转杆固定于拖车的侧桥上，横流向的角位移不受约束，而约束其他5个方向位移；模型水下端为自由端。射流装置由铜管、自吸离心水泵、流量仪和带钢箍的连接管组成(见总体布置图1)。铜管底端封闭，外径为25 mm，且沿其前驻点线在铜管底端开小圆孔。依据底端对齐、母线平行的原则将细铜管固定于模型首部前驻点线处，且圆孔外法向与拖车前进方向一致。铜管顶端经连接管与流量计，阀门和水泵相连。水泵另一端的连接管置于水池中。流量计和水泵固定放置在拖车上，垫有厚20 mm橡胶以减振。当水泵开启时，泵一端的连接管从水池中抽水，并通过另一端的阀门、流量计和连接管给铜管内注入水流，由水下圆孔形成定常射流。实验中标定拖车行进方向为x轴正方向，横流向为y轴，竖直向上为z轴正方向。

为研究射流流量对模型振荡抑制效果的影响，根据实验条件，本实验设计了开孔数(N)分别为5、10、20，相邻两孔中心距c依次为0.2 m、0.1 m、0.05 m的测试状态(注：最底端的首个孔心为基准)。实验时水温为15 ℃。模型安装图见图2。

流量计采用KROHNE高精度电磁流量计(OPTIFLUX2300C型)，其测量流速范围-12～12 m/s，测量精度为0.2% MV+1 mm/s；水泵的功率为1 500 W，最大流量为18 m3/h，最大扬程为25 m，最大吸程为8 m。

圆柱模型只沿横流向(y向)上发生摆动，采用Qualisys光学运动捕捉系统对其运动轨迹进行测量。该系统由光球、高速摄像机(Oqus 3型)和QTM数据软件组成。高速摄像机镜头采样频率可达10 kHz，最大视频帧率10 000 帧/s。QTM数据软件可以输出物体运动数据(如速度、位移、旋转角度等)，并能对运动进行轨迹分析，如图3所示。本实验中采样频率为50 Hz。

图3 Qualisys运动捕捉系统

Qualisys运动捕捉系统通过追踪安装在圆柱顶部的3个光球的位置变化，来定义和采集圆柱的运动数据，3个光球的安装高度、角度各不相同，确保了圆柱模型运动过程中3个光球在镜头中互不遮挡，运动轨迹能完全被Qualisys系统捕捉到。布置方案如图2所示。

为便于分析实验结果，引入计算参数：

Q=ULD

(1)

(2)

(3)

(4)

式中：Q、q分别为圆柱浸水截面流量和总射流流量，m3/s;U、Uj分别为拖车速度和每个射流孔的平均速度, m/s；d为射流孔直径，m；p为单位时间每个射流孔的平均动量，kg·m/s；ρ为流体密度，kg/m3；N为孔数；St为斯特罗哈尔数；f为模型的振荡频率，Hz；fn为模型固有频率，Hz。

3 实验结果分析

刚性圆柱在涡激力的升力作用下做摆动时，圆柱整体的角速度是相同的，圆柱底部距转轴距离最大，摆幅最大，更易于观测。因此实验选取圆柱底部中心点为监测点，测量该点垂直于流向的横向位移的实时变化，以此量化圆柱涡激振荡的振幅与频率进行讨论和分析。

实验首先对射流模型无流速时(q=0，Q=0)进行自由衰减实验测试获得模型的固有频率fn，如图4所示，fn为0.128 Hz。实验时的拖车速度为0.15 m/s，此时雷诺数Re=2.4×104，对应的约化速度为7.32。

图4 自由衰减时历曲线

启动拖车让其速度稳定达0.15 m/s，测得柱体的横向振荡位移Δ(mm)。图5给出了Δ随时间t的变化规律。显然在涡激励升力的作用下，射流模型中模型沿垂直于流速方向产生显著的周期性的横向振荡，在t=25 s后Δ达到平稳，为便于统计引入Δ的峰峰值(一个周期内位移最高值和最低值间的差值)进行定量分析。统计测点在稳定段时位移的平均峰峰值Δpp和振荡主频f，模型振荡特性见表1。射流(q≠0)对模型横向振荡的抑制程度以同雷诺数时无射流时模型的振荡特性作为基准值进行讨论和分析。

图5 监测点横向位移时历曲线

表1 射流模型振荡特性表

为保证实验测试的准确性，本实验设计同开孔数射流流量不同的多组测试和不同开孔数不同射流流量的组合测试，以获得射流对模型振荡的抑制规律，同时将位移峰峰值Δpp和射流流量无量纲化(Δpp/D，q/Q)，测试工况见表2。

表2 测试工况

3.1 横向位移响应

图6 给出了3组不同开孔数、不同射流流量的模型横向位移峰峰值的变化曲线。由3组的整体测点曲线变化趋势来看都呈现出“Z”型分布的状态，但对射流流量q/Q的敏感程度不同。根据振荡位移峰峰值Δpp/D的变化规律明显地可以从图7中看出2种显著模式：高振幅稳定模式和低振幅稳定模式，显然横向位移存在3个区域：高振幅区、过渡区和低振幅区：

高振幅区：Δpp/D≥2.32;

过渡区： 0.66<Δpp/D<2.32;

低振幅区： 0≤Δpp/D≤0.66。

在高振幅区，开孔数量和射流流量没有使模型振荡位移峰峰值Δpp/D减小，反而使其略有增大。尤其是开孔数N=5和N=20，q/Q在0.01～0.017 5时，增幅在10%附近，但Δpp/D的变化很平稳；当q/Q>0.0175时，N=5和N=20这2组射流状态下的Δpp/D在过渡区内都出现陡然下降的现象，Δpp/D由2.32降到了0.66，振幅峰峰值降低率高达70%以上。可见，过渡区是射流对振荡影响变化最大的区间。但Δpp/D对射流流量的敏感度不同。N=10对射流流量的敏感度很高，在q/Q大于0.010时就发生振荡陡降的现象。而N=5和20相对来看对射流流量的敏感度较低，即需要较高的射流流量射流才能起到降低振荡位移的作用，尤其是N=5要q/Q大于0.017 5、N=20要q/Q大于0.016射流才起到抑制作用；在低振幅区，随着q/Q的继续增加其对Δpp/D并没有显著的降低作用。同时N=20反而出现了Δpp/D略有增大的趋势。

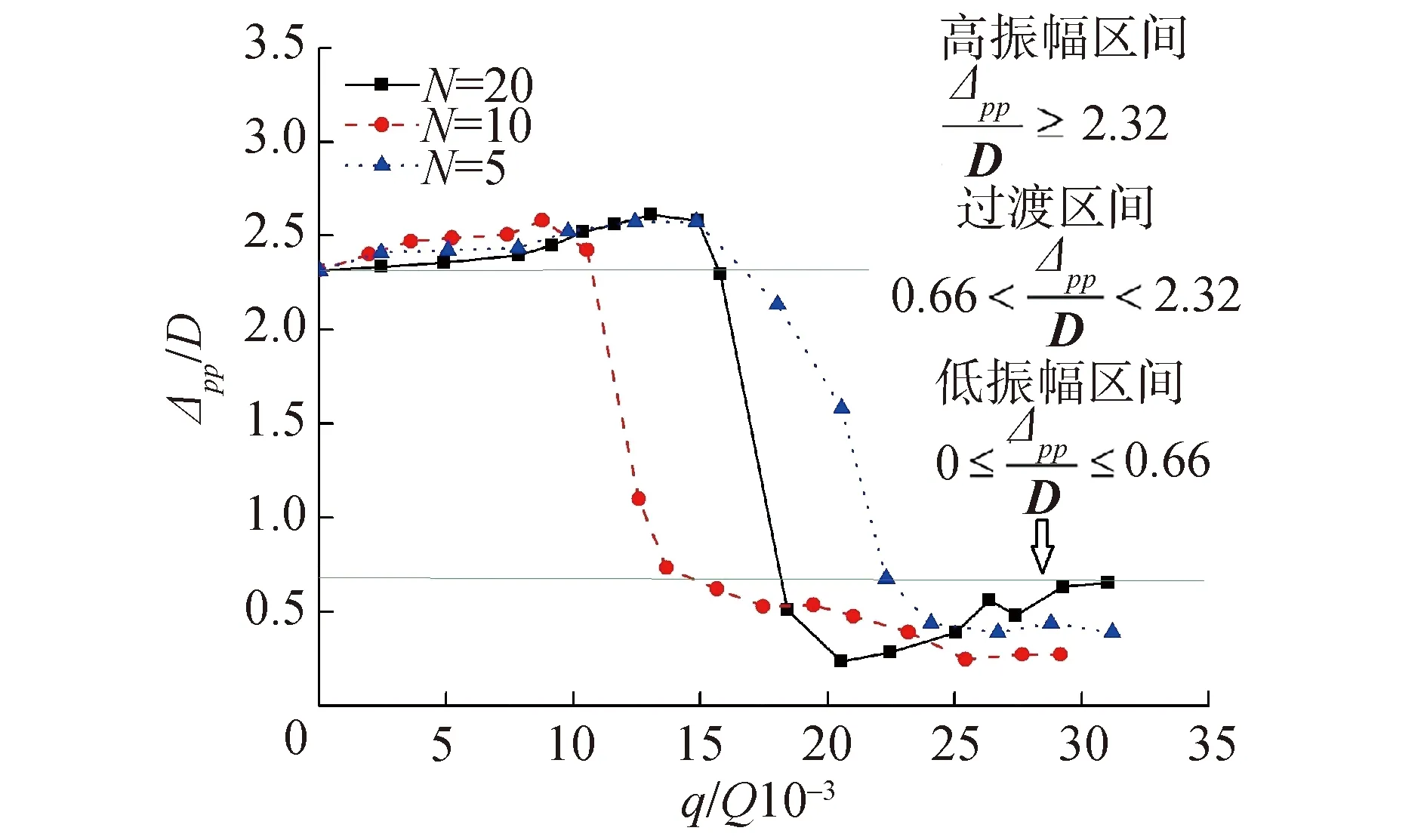
图6 横向振荡位移随射流流量的变化

图6中Δpp/D发生陡降时对应的射流流量不同，这是因为不同开孔分布形式对应的沿圆柱展向的涡脱相关长度也会有所不同，相对于通过变更分离点和生成扰动来影响横截面的局部受力和阻尼这类常见的二维影响，改变展向涡脱相关长度则是一种三维的影响，其具体规律还需进一步深入研究。

由图6可见在高振幅区和低振幅区，开孔数N的增加和q/Q的增加对模型摆动的振幅峰峰值Δpp/D影响不大，而在过渡区N和q/Q对Δpp/D的影响较大，因此为进一步量化分析首部射流对单自由度圆柱涡激振荡的影响，本文在2个区间内各选取一个典型工况进行量化分析：高振幅区间内选N=20，q/Q=0.013；低振幅区选N=10，q/Q=0.029。

图7(a)和图9(a)分别给出了高振幅区位移Δ的时历测试对比图和位移的PSD图。明显可以看出模型在拖车启动后开始进入摆动状态，振幅逐渐增大在t=100 s达到稳定状态，但射流同步开启并未见到在稳定段使得Δ减少，Δ仍在±200 mm附近振荡。而当射流停止时，即q/Q=0，Δ值反而出现降低的现象，使得位移的降低率为-11.71%(见表3)。虽然模型的固有频率为0.128 Hz，而有射流时的振荡频率为0.11 Hz，显然振荡频率错开了模型的固有频率不会产生共振，但当启动射流在q/Q=0.013时横向位移的PSD值远大于无射流时的，这说明射流给运动流体注入了一定的能量，很可能会增强振荡柱体前缘来流的湍流动能，使得分离的涡流所诱发的横向流体升力增加，因此横向位移呈现出增大的现象，射流不能起到降低模型横向位移的作用。但在此区，射流使柱体的振荡频率有明显的降低，降低率达到23.49%(见图7和表3)。

图7 横向位移时历测试曲线

表3 典型工况横向振幅对比

在低振幅区，射流呈现出对柱体横向振荡显著的抑制作用。图7(b)给出了在低振幅区射流流量对横向位移时历曲线的影响对比。在无射流时(q/Q=0)模型的横向位移Δ在±200 mm附近波动，启动射流射流，射流流量达到q/Q=0.013(N=10)并达到稳定时Δ显著地降低，在±50 mm附近波动。Δpp值发生显著的减低，横向位移的抑制率高达84.87%。

3.2 横向位移的频谱

为了进一步分析射流流量对模型横向振荡频率的影响，使用功率谱变换(PSD)对横向位移进行了频谱的对比分析。图8给出了高、低振幅区各个射流流量下模型振荡频率对应的斯特哈尔数(St)的变化。显然，在高振幅区随着q/Q的增加，St数逐渐减小；而在低振幅区，随着q/Q增加使St先稳定在0.125附近q/Q的继续增加St迅速增大。图9和表4分别给出了高、低振幅区的2个典型射流工况的横向位移的功率谱对比图和振频变化率的对比。在各个射流流量时，频谱成分中体现的是单峰主频特性，1阶谐频占主导地位。频谱中无谐频的现象发生。高振幅区，射流量虽然较低但会使得模型的振荡频率显著减低，与无射流时模型的振荡频率相比变化率(下同)在23%附近；随着q/Q的增大模型的横向位移进入到低振幅区，模型的横向振荡频率仍保持降低的状态，但当q/Q=0.029时频率的变化率减少，仅在6%附近。此频率下对应的能量接近于0，其值远远小于q/Q=0时的能量。这正解释了低振幅区增加射流后横向位移减小原因。综上，在不同的振幅区域射流流量对模型振荡频率变化程度和规律是不一样的。在低振幅区，随q/Q的增加，振动频率会有所增大，在高振幅区变化规律正好与其相反。由图9(b)也可看出无射流时横向位移具有很大的能量。

图8 斯特哈尔数

图9 横向位移频谱图

表4 典型工况横向振荡频率对比

4 结论

1) 射流对模型横向振荡的减少程度表现出两种不同的模式：即横向位移突然、明显的降低和随后位移进入到一种饱和状态，之后没有发现横向位移的进一步降低。

2) 射流的开孔N对模型横向位移随射流流量变化的敏感度有很大影响。

3)q/Q>0.025时模型的振荡进入低振幅区，射流使得模型的横向位移减少近85%；但随q/Q的增大，相对于无射流时振荡频率的变化明显减少。