波能装置浮子选型及水动力性能分析

孙科， 解光慈， 周斌珍

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001; 2.中山大学 海洋工程与技术学院，广东 珠海 519082； 3.华南理工大学 土木与交通学院,广东 广州 510000)

波浪能作为一种新型的海洋可再生能源，具有储量大、分布广的特点[1]。而波浪能装置的形式也是多种多样的，有点吸收式、振荡水柱式以及越浪式等[2]。如今，越来越多的国家研究波浪能利用技术，主要研究方面包括波能转换水动力研究、PTO系统研究以及波能浮子与平台的耦合运动等[3]。其中浮子的形状很大程度上决定了其水动力性能。

对于波浪能浮子的研究方法有很多种，最常用的方法有基于势流理论的边界元法和基于N-S方程的计算流体动力学(CFD)方法。

在波浪的研究中，势流理论一直占据主导地位。2013年，周斌珍等[4]利用高阶边界元研究波浪与结构物的非线性相互作用；张万超等[5]在2016年基于势流理论对轴对称浮子进行水动力特性研究。Zhang等[6]基于势流理论和高阶边界元法，建立了只考虑双浮体垂荡运动的数值模型，研究其水动力性能和时域响应。常见的基于势流理论的软件有WAMIT、AQWA以及SEASUM。然而由于其无旋无粘的前提假设，使得这一理论只适用于处理一些大结构物或者粘性影响并不显著的流动问题。

而随着计算机性能的不断发展，计算流体动力学随之诞生，通过对整个计算域离散化，利用有限差分法、有限体积法等方法计算。CFD方法能够考虑物体的粘性，并且可对复杂几何形状的物体计算，因此成为许多研究者们的选择。国威[7]在2016年基于CFD方法模拟浮子的线性波上浪、非线性波抨击及自由面形变的时域非线性问题；Bhinde等[8]在2009年基于CFD方法研究一种点吸收式的波能浮子的水动力特性以及几何形状的优化并与实验作对比；Ransley等[9]在2017年基于CFD方法研究波能浮子在极端海况的生存能力；Wang[10]通过综述近年来用CFD数值方法解决的船舶与海洋工程中的复杂问题，讨论了立管涡激振动、浮式风力机以及高速船在波浪中的运动等方面的引用，来描述计算流体力学技术的发展。常见的CFD商用软件有CFX、STARCCM+以及FLUENT等。然而CFD方法对于网格的数量及质量要求很高，计算时间长，对计算机性能要求高，不适合大范围的算例计算。

对于波浪能装换装置来说，浮子选型对能量转换效率有很大影响，国内外学者针对这一方面做出了大量研究。张亮等[11]基于CFD方法研究圆柱和圆台浮子的阻尼系数、浮子质量对装置性能的影响规律。Zhang等[12]通过边界离散化(BDM)的半解析方法分析复杂轴对称浮体，分析对比了圆柱、锥形以及半球形浮子的水动力性能。然而以上研究对于浮子形状分类较少以及没有结合分析流场机理。而关于粘性修正方面，同样也有许多学者在研究，Liu等[13]在对浮体进行分析时，通过在自由表面边界中引入耗散项来考虑粘性效应。田博等[14]基于RANS所求得的水动力系数与势流理论结合进行粘性修正，对单体复合船型运动预报方法进行研究。

本文利用CFD与势流理论结合的方法，能够减少大量计算时间。通过CFD模拟自由衰减估算粘性力，再以势流理论的方法加上粘性力对波能浮子的几何形状进行研究，分析平底圆柱浮子的直径吃水比对粘性力、运动响应及俘获宽度比的影响；对比不同底部角度锥形浮子运动响应及俘获宽度比，选择最优宽角度。

1 波能浮子数学模型的建立

当波浪传递时，波能浮子受到波浪作用产生垂荡作用，使得浮子与PTO产生相对的位移，进而产生能量。因此在数学模型建立时只考虑浮子垂荡方向的运动。对于圆柱形波能浮子，质量为m，半径为a,如图1。

图1 波能浮子运动模型

对于单自由度波能浮子，可用水面浮体的运动表示，建立运动方程为：

(1)

(2)

Fs=Cx=ρgπa2x

(3)

(4)

Fk=Kx3

(5)

式中：Fe波浪激励力；Fr辐射力；Fs静水回复力；Fc线性PTO阻尼力；Fk弹簧力；μ33浮子附加质量；λ33浮子辐射阻尼；ρ为水的密度；g为重力加速度；CpPTO阻尼力系数；K为弹簧系数。

将各项代入得：

(6)

在线性势流理论中，浮子在波浪中运动时所受的力可分为入射力、绕射力以及辐射力、入射力和绕射力统称为波浪激励力。在实际水域中，浮子由于受到粘性影响，其运动响应尤其在共振频率下远远小于势流理论所得结果，流体粘性力是导致这一结果的主要原因。Son等[15]对圆柱浮子进行波浪能装置实验时发现，势流理论所得波浪激励力结果与实验所测基本相同，因此，波浪激励力项受粘性影响不大。但对于辐射力项，尤其是阻尼项，试验和势流的结果相差很大，粘性效应不可忽略。为了能够得到浮子的粘性力，Journée等[16]曾通过自由衰减曲线推导浮子的粘性力公式，当浮子仅考虑垂荡运动时，其垂荡自由衰减线性运动方程为：

(7)

化简后得：

(8)

设无量纲系数k：

(9)

(10)

(11)

x3(t)=x3,ae-vt[cos(ωvt)+sin(ωvt)]

(12)

设x3(t)周期为Tv，求解：

x3(t)/x3(t+Tv)=evTv

(13)

化简得：

vTv=kω0Tv=ln(x3(t)/x3(t+Tv))

(14)

ω0Tv=ωvTv

(15)

继而可以推导无量纲阻尼：

(16)

为了防止由于零点漂移原因使得所得数据不准，通过计算衰减曲线的双振幅数值，来避免这种误差。

(17)

式中x3,k为第k个峰值点的幅值。

式(17)能够通过自由衰减曲线得到无量纲系数k，进而估算粘性阻尼系数:

λvis=2kρgπa2/ω0

(18)

最终推导出浮子固有频率时的粘性阻尼，Tom[17]在实验中证明，波浪频率变化对粘性效应影响不大，因此可以通过以上方法算出固有频率下的总阻尼系数。结合Tom的结论，可以大致计算出粘性阻尼，从而对整个频域进行修正。

浮子粘性阻尼计算：

λv=λvis-λn

(19)

因此，通过上述论述，得到浮子在垂直方向的运动方程：

(20)

式中λn为共振频率下浮子辐射阻尼。

每个波浪频率下，浮子的输出功率存在最优阻尼系数，即cp为某一值时，输出功率最大：

(21)

2 数值模拟方法

利用CFD软件Star-CCM+来模拟浮子自由衰减，进而算出粘性系数。模型设置的是一个四周壁面的三维水池，浮子自由衰减所兴的波会向四周传递，由于水池大小有限，需要考虑壁面效应，因此设置阻尼消波。

模拟中涉及到空气与水的多项流，应用流体体积(VOF)法捕捉空气相和水相之间的自由表面，因此需要对液面附近做网格加密，浮子运动区域也同样需要设置网格加密，并且为了网格尺寸能够平滑过渡，设置过渡层。网格设置如图2所示：

图2 CFD模型网格划分

网格划分及模型设置是CFD前处理必不可少的，理论上来讲，网格密度越高，计算精度越高，但同样计算时间会增加。时间步长对于模拟是否能够收敛也有很大影响。合适的网格尺寸和时间步长对计算精度和计算效率改善有着很好的效果。本文设置了3个测试模型，选择2a/d=1.6的圆柱浮子，d为浮子吃水，T为浮子共振周期。其时间步长和网格大小设置如表1所示，模拟结果如图3所示，根据3个模型数据得出粘性阻尼，并与模型1对比得相对误差，如表2所示。由表2可知当网格及时间步长选择d/30和T/400时，所得结果与另外2组相差不大，数据差异小于5%，因此d/30和T/400的网格及时间步长满足收敛性要求。

表1 自由衰减模型时间步长与网格尺寸设置

自由衰减模拟除了对网格大小及时间步长收敛性验证以外，还要对其进行准确性验证。Tom[17]研究了圆柱浮子的水动力性能，并做了相关浮子自由衰减实验，将CFD数值模拟所得数据与其试验数据作对比。

图3 网格尺寸和时间步长收敛性验证

表2 粘性阻尼相对误差

观察图4，模拟数据与实验数据，在周期上几乎吻合，而在衰减曲线上，实验数据后几个周期略大于模拟数据，数据差别小于5%，验证了数值模型的准确性。

图4 自由衰减运动验证

根据得到的粘性系数以及推导的运动方程，求解浮子的频域运动响应。为了验证其修正数值的精度，将其与CFD模拟的波浪下浮子运动作对比，模型选择2a/d=1.6的圆柱浮子，周期T=2.17 s，波高H=0.2 m，所设置阻尼均为最优阻尼，得到图5。

图5 CFD模拟与粘性修正方法对比

综合以上数据对比，基于粘性修正的势流理论方法与CFD模拟相比，在共振频率附近有轻微的差别，垂荡运动响应结果基本一致，说明可以通过粘性修正方法来估算浮子运动，减少计算量，增加计算效率。

3 平底圆柱浮子的水动力性能分析

由于平底圆柱形浮子几何特征只有直径2a和吃水d，因此几何特征形状用无量纲参数2a/d来表示。通过改变直径吃水比，来改变浮子几何尺度，更加全面地分析不同尺度浮子的水动力性能。为了更好地观察不同直径吃水比下浮子的粘性影响，定义阻尼粘性效应的无量纲表示为：

(22)

通过STARCCM++模拟浮子的自由衰减，代入粘性修正公式，并将其无量纲化，得到不同2a/d下浮子的粘性系数变化。

图6 平底圆柱浮子阻尼修正系数随2 a/d变化关系

图7中浮子的运动响应峰值随2a/d的增加而减小，当频率过大或者过小时，不同比例的浮子运动响应差距不大。当ω>2 rad/s左右时，运动响应开始上升，且2a/d越大上升得越早，同时下降得也早；当ω>5 rad/s左右时，所有比例基本重合。

图8中浮子俘获宽度比(CWR)随着2a/d的增大其峰值逐渐增加，其所俘获大功率的频率范围也更大，即有效频域宽度更大。此外随着2a/d的增加，浮子的峰值所处频率也在不断减小，当2a/d=0.4时，峰值点处ω=2.9 rad/s，当2a/d=3.6时，峰值点处ω=2 rad/s，可以通过调节尺寸选择适合海域的浮子。大部分海域都有一段频繁出现波浪周期。根据多发的波浪频率设计相应尺寸的浮子，对于工程应用具有重大意义。

图7 圆柱浮子频域运动响应

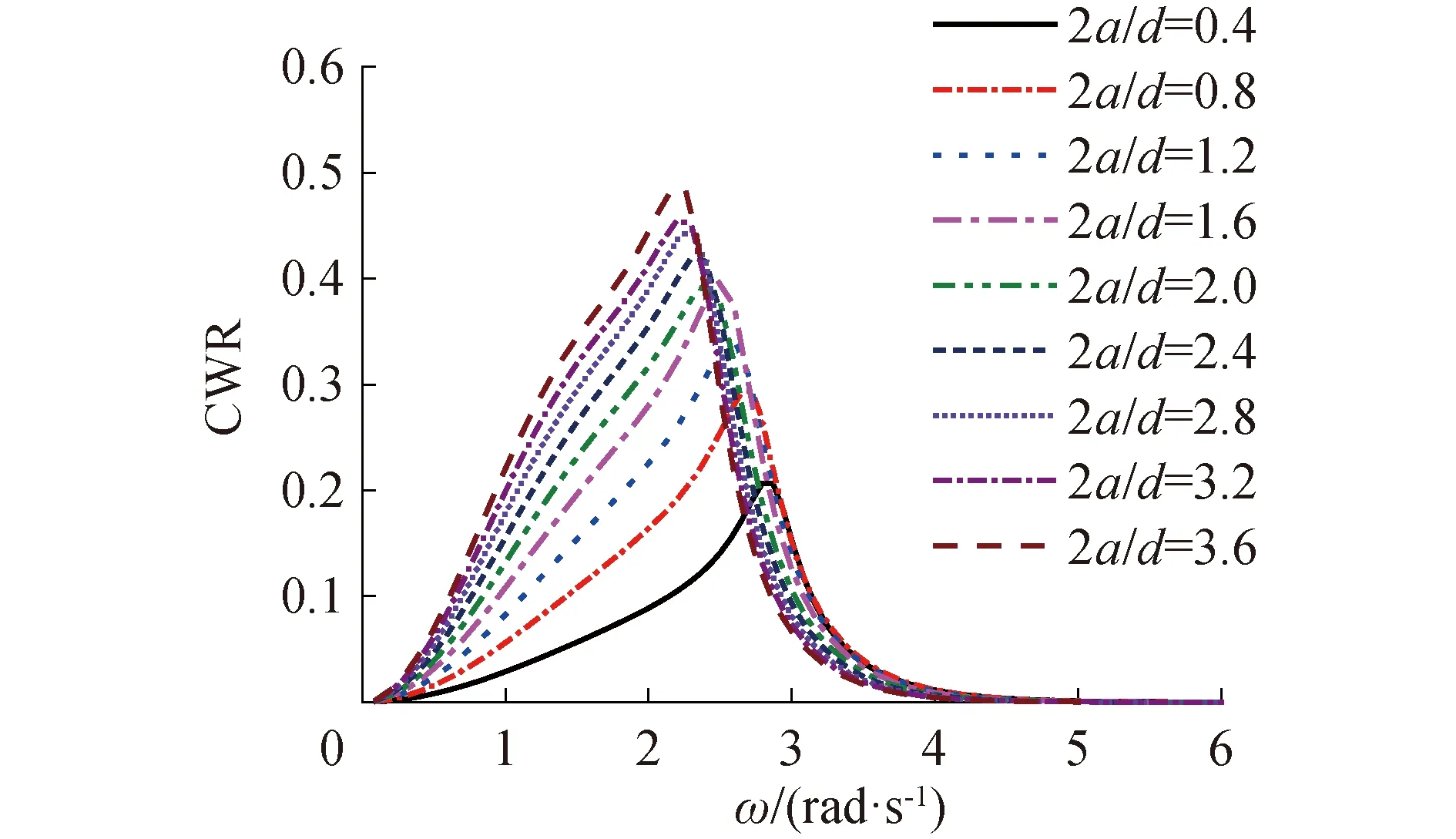
图8 圆柱浮子频域俘获宽度比

4 锥底浮子的水动能性能分析

分析完浮子2a/d对平底浮子水动力性能的影响，接下来分析锥底浮子底部形状对水动力性能的影响，选择4种浮子进行分析，分别是α=90°,120°,150°,180°(即平底圆柱浮子),如图9所示。

图9 浮子形状

选择尺寸2a/d=1.6，4个浮子排水体积相同，锥底浮子的等效吃水与平底圆柱浮子的相同。

由图10可知阻尼修正系数随着角度的增大而增大，即底部形状的角度越小所受粘性影响越小。计算浮子的运动响应以及俘获宽度比，由图11可以观察到，不同锥底角度的浮子，其共振频率有细微的变化，当角度变小时，因为小角度锥底浮子所受粘性影响小，其运动响应就随之增大。观察俘获宽度比变化图可知随着角度的减小，其俘获宽度比的峰值增大，且有效频域宽度也随之增大，更加有利于对波浪功率的俘获,如图12所示。然而在工程实际利用中，当锥底角度越来越小，为保证其排水体积不变，长度就会随之增加，不利于浮子的安装以及整个装置的运行，因此，对于适合角度的锥底浮子需要根据实际情况决定。

图10 浮子阻尼修正系数随底部角度变化关系

图11 不同底部形状浮子运动响应

图12 不同底部形状浮子俘获宽度比

在使用粘性修正的方法计算浮子水动力系数后，为保证数值模拟的准确性，需要利用CFD方法进一步分析计算，通过模拟浮子在波浪下的运动流场，分析流场结构和变化机理，进一步检验线性计算结果的可靠性。本文利用Star-CCM+模拟4个浮子在共振周期附近的波浪下的运动，监测其流场涡的变化，波浪为从右向左传递。

由图13～16为4个浮子在在一个周期内的浮子周围涡量场图，不难看出，迎着波浪的这一侧会产生较大的涡，因为受到浮子阻碍的流体与波浪传递过来的流体之间产生了较大的速度梯度，从而产生了涡。图中，浮子锥底角度越大，附近涡量分布越紊乱，涡分布的范围越大，其中90°锥底浮子涡分布范围很小，仅在浮子下方有一部分，而180°平底浮子流场涡分布范围最广。这也就会导致波浪能能量的耗散增加，影响浮子对能量的吸收，进而影响效率。可以看出，主要产生涡的部位是圆柱转为圆锥处的拐角，这是因为几何尺寸突然变化，导致流体的速度梯度也变大，容易产生涡。并且锥底角度越大，其尺寸变化幅度也就越大，所产生的大量级的涡也越多，这说明波浪能量通过浮子壁面将能量传递给了流体质点，变成了流体质点的动能。意味着运动过程中耗散的能量增加，这些耗散的能量无法被吸收，而入射波能量固定，这就导致锥底角度小的浮子能量利用率高于角度大的浮子。

图13 各浮子在t=NT+T/4时的涡量场

图14 各浮子在t=NT+T/2时的涡量场

图15 各浮子在t=NT+T3/4时的涡量场

图16 各浮子在t=(N+1)T时的涡量场

5 结论

1) 对于平底圆柱浮子，研究了不同直径吃水比的粘性阻尼大小及水动力性能，圆柱浮子越矮胖，其所受粘性阻尼越小，并且随着2a/d的增大，浮子俘获宽度比的峰值区域也会改变。

2) 对于锥底圆柱浮子，分析了不同锥底角度浮子的水动力性能，当锥底角度较小时，更有利于浮子对波浪能量的俘获。

3) 通过对浮子进行时域流场分析，得到锥底角度大的浮子容易产生较大范围及量级的涡，影响波浪能量的吸收,与频域分析结果一致。