基于结构性参数的土本构模型研究

李 吴 刚，杨 钢，刘 文 化，孙 秀 丽

( 1.江南大学 环境与土木工程学院，江苏 无锡 214122；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024 )

0 引 言

由Roscoe等[1]提出的剑桥模型能够较准确地描述重塑土的力学特性，而自然界中的土在漫长的地质作用下，土颗粒形成某种特定的空间排列形式或在土颗粒间形成胶结作用力，导致土体表现出结构性特征，对土体的强度和变形特性产生极大的影响，使得结构性土的力学特性与重塑土相比存在较大差异[2-5]．结构性可提高土骨架的稳定性，在相同应力条件下，未达到屈服状态的结构性土常可维持更高的孔隙比；当达到屈服后，土体结构的破坏使得结构性土的压缩指数显著增大[6-8]．此外，结构性土的应力-应变曲线与围压的大小有关，在高围压条件下，土体的结构破坏较多，结构性土的应力-应变曲线与重塑土的应力-应变曲线较为相似，为应变硬化[9]；在低围压条件下，土体结构较为完整，则结构性土的应力-应变曲线为应变软化，其抗剪强度达到峰值强度后迅速降低并趋近残余强度[10-11]．剑桥模型建立于重塑土的试验基础之上，未考虑结构性对土体力学特性的影响，故无法预测结构性土的力学与变形特性．而结构性土广泛存在于工程实践中，若采用不考虑结构性影响的本构模型用于指导工程实践，会影响土工结构在使用过程中的可靠性．将结构性对土体力学性质的影响引入土的本构模型，可更加合理地解释原状土的力学与变形特性，优化土工结构的设计，并可提高其在使用过程中的可靠性．

近年来，关于土的结构性研究已取得很大发展．沈珠江[12]根据结构性土压缩曲线的特点，认为结构性土具有明显的初始屈服面，在初始屈服面内的变形为弹性变形，基于损伤力学理论建立了结构性黏土的弹塑性损伤模型．周成等[13]、孙吉主等[14]也分别基于损伤力学的观点建立了结构性土的本构模型．但根据损伤理论建立的本构模型难以解释扰动土体可能发生的强度增长，扰动状态概念模型[15]较好地解决了结构性土损伤本构模型的缺陷．王国欣等[16]、Desai等[17]、Liu等[18]分别基于扰动状态概念模型建立了结构性土的本构模型，但该类模型中的参量较难从传统土力学试验确定，限制了该类模型的应用．近年来，有学者采用结构性参数建立结构性土的本构模型，如Liu等[19]以剑桥模型为基础，采用初始结构屈服应力描述结构性土的体变关系，建立了结构性剑桥模型(SCC)；Suebsuk等[20]以边界面理论为基础，将结构性剑桥模型扩展至可描述超固结结构性土的力学与变形特性；Nakai等[21]引入虚密度表示结构性土颗粒间的联结作用，建立了结构性土的压缩曲线方程；祝恩阳等[22]通过加载过程中结构势的衰减描述结构性土的体变，在统一硬化模型的基础上建立了结构性土的本构模型．

由于土颗粒形成特定的排列形式和颗粒间形成的胶结作用，结构性土在宏观力学性质上表现出结构性特征．建立结构性土本构模型的关键在于如何在本构中引入代表土体结构性的相关参数并通过该参数描述结构性对土体力学特性的影响．本文以结构性土的变形特性为基础，分析结构性对土体力学特性的影响，提出用于表征结构性的参数，建立结构性土的本构模型，模型参数具有较明确的物理意义，并可通过常规土力学试验确定，便于模型的工程应用．

1 理论分析

1.1 结构性土的体变特性

图1为希腊科林斯运河泥灰土的压缩曲线[23]，该土具有较强的结构性．由图1中所示的压缩试验结果可知，该土具有明显的屈服应力．在达到屈服之前，结构性土的压缩曲线基本为弹性变化．当达到屈服后，土的结构性开始发生破坏，此时结构性土的压缩系数显著增大，土体的变形显著发展．当结构性完全破坏时，发展为完全扰动土．由试验结果可知在土体结构未发生破坏前结构性土的体变特性可用弹性关系表示，假设在弹性阶段随着土体应力的增长，土的结构总保持完整且不发生破坏(如图2中虚线所示)．此时，结构性土的体变增量与应力增量可采用下式表示：

(1)

其中e为孔隙比，p′为平均有效应力，κ′为图2中虚线的斜率．该曲线表征了结构性完整且在荷载作用下土体结构不发生破坏的结构性土的固有压缩特性，将其定义为结构性土的本征压缩曲线(ISCL)．结构性土中的微小土体单元具有一定的结构强度，故在相同的应力状态时，结构性土可维持较大的孔隙比，其压缩曲线往往位于重塑土压缩曲线的上方．随着应力的不断增加，土的结构性发生破坏，此时结构性土开始产生塑性变形．当土的结构发生破坏时，结构性土的变形特性由结构性发生破坏的扰动土体单元和结构性完整的非扰动土体单元的变形特点共同决定，并随着应力的增加，土的结构性破坏急剧增长．在宏观上表现为土的体变显著增加，如图2所示．当土的结构完全破坏时，结构性土的压缩曲线与重塑土的压缩曲线重合，故正常固结状态时结构性土的压缩曲线(SCL)位于以结构性土的本征压缩曲线和重塑土的正常固结线(NCL)为边界的扇形区域之间(图2)．

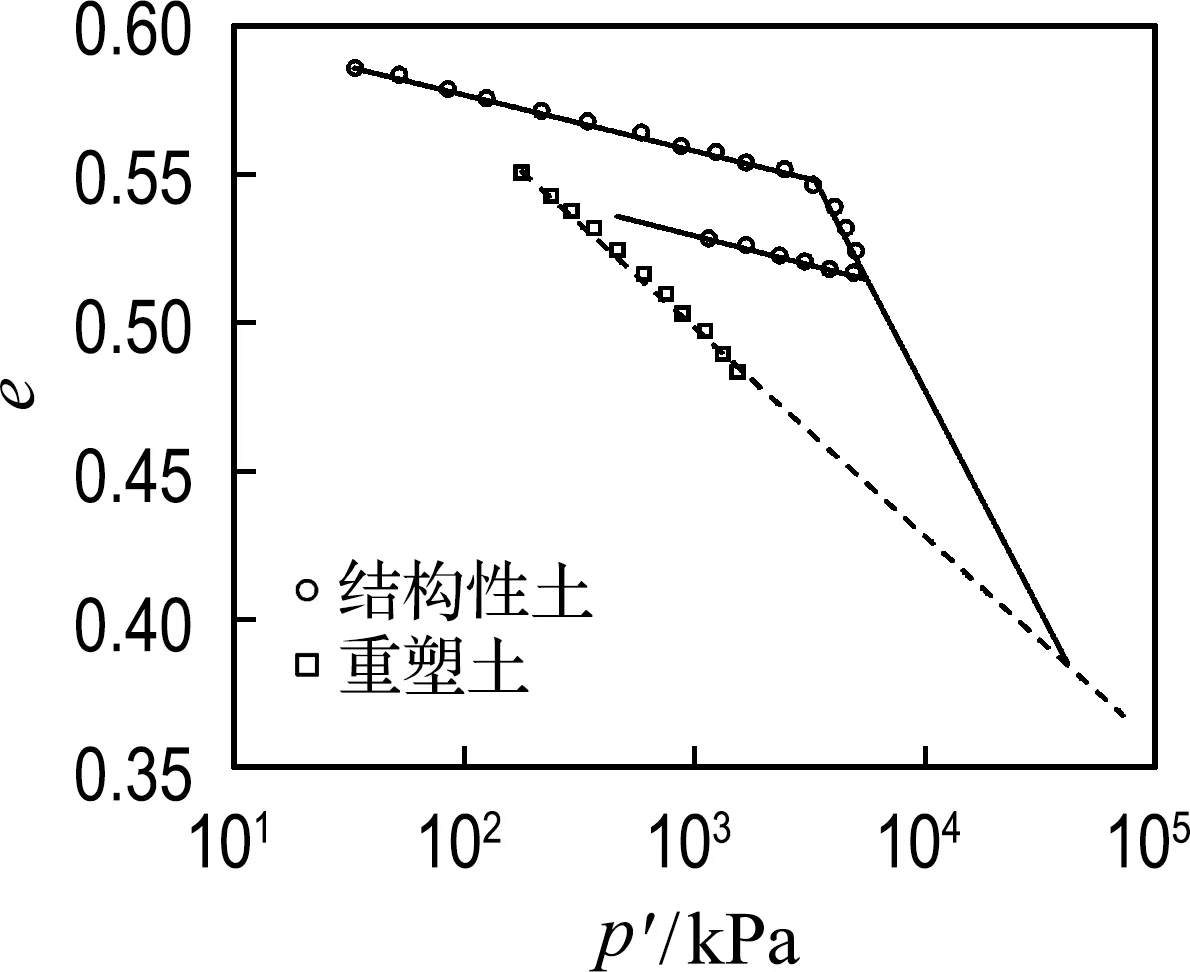
图1 科林斯运河泥灰土的压缩曲线

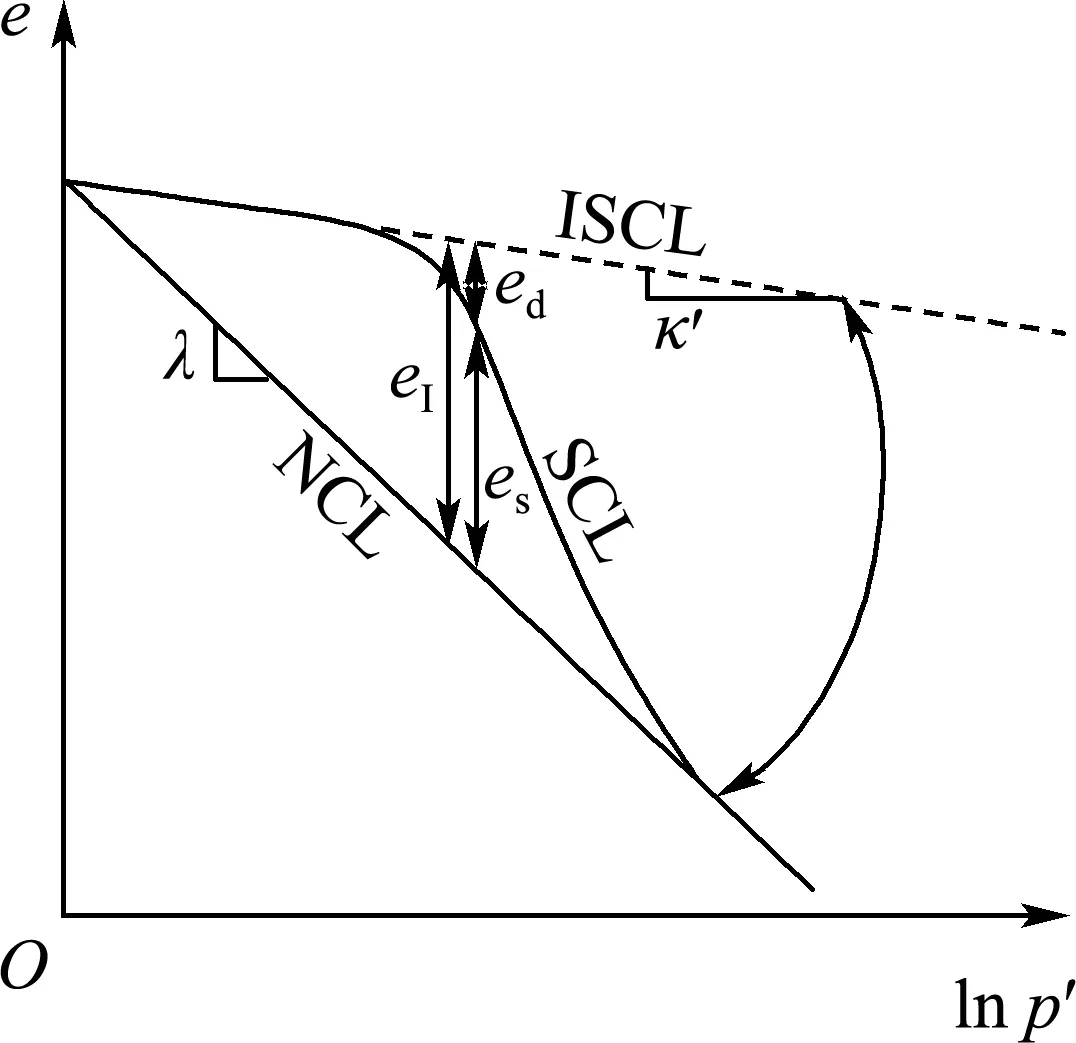
图2 结构性土的压缩曲线

建立结构性土本构模型的关键在于如何描述土体的结构性和荷载作用下结构性的衰退规律．假设有一结构性完整即未发生扰动的试样，试样在荷载的作用下初始段的变形为弹性变形，压缩曲线的斜率为κ′，如图2所示，以ed表示SCL和ISCL之间的距离，es表示SCL和NCL之间的距离，eI表示ISCL和NCL之间的距离．当结构性土体单元未发生破坏时，结构性土在压缩过程中仅发生弹性变形，ed为0，eI与es相等，此时es/eI的值为1．由于结构性土内各土体单元的结构性强度并不相同，故在荷载增加的情况下结构性强度较弱的土体单元先发生破坏，并且随着荷载的增加，结构性土体单元的破坏扩展至相邻的土体单元，土体内部的损伤开始扩展，土颗粒间发生滑移，结构性团块破碎，结构性土产生塑性变形．在此过程中，ed、eI和ed/eI的值随着荷载的增大而增大，但es/eI的值开始减小；当荷载继续增加时，破损的结构性土体单元数量也随之增加，es/eI的值随着变形的发展不断减小；当土中的结构性土体单元全部破坏时，结构性土变为完全扰动土，结构性土的压缩曲线与重塑土的压缩曲线重合，此时，es和es/eI的值为0，ed与eI的值相等．

由上述分析可知，在外荷载作用下，土体结构性的衰退伴随着es/eI值的不断减小，故本文采用下式表征土体的结构性变化：

(2)

其中ξ为结构性因子，其变化范围为0～1．假设某结构性完整的土样，在荷载作用下，土内不发生结构性破坏，则其ξ恒定为1；随着荷载的增加，土样发生塑性变形，土的结构性发生破坏，则其ξ逐渐减小；随着荷载继续增加，当土内的结构性完全破坏时，结构性土退化为重塑土，此时其ξ为0，并且随着荷载的继续增加，其ξ恒定为0．

1.2 体变方程

重塑土在压缩过程中的体变方程可采用下式表示：

(3)

其中p′0为初始状态时的平均有效应力，e0为初始状态时的孔隙比，λ为重塑土压缩曲线的斜率．

根据结构性因子的定义及图2中重塑土与结构性土压缩曲线之间的关系，结构性土的孔隙比可表示为

(4)

其中es可通过引入结构性因子ξ表示为如下形式：

es=ξeI

(5)

其中eI表征了在相同的有效应力条件下结构性土的本征压缩曲线和重塑土的压缩曲线间孔隙比的变化，可采用下式表示：

(6)

将式(5)、(6)代入式(4)后可得：

(7)

将式(7)表示为增量形式，则有

(8)

由式(8)可知结构性土的压缩变形由两部分组成：由应力增加导致的孔隙比改变和结构性因子变化导致的孔隙比改变，如图3所示．若结构性土在压缩过程中结构性因子ξ保持恒定，则试样压缩曲线的斜率为(1-ξ)λ+ξκ′．

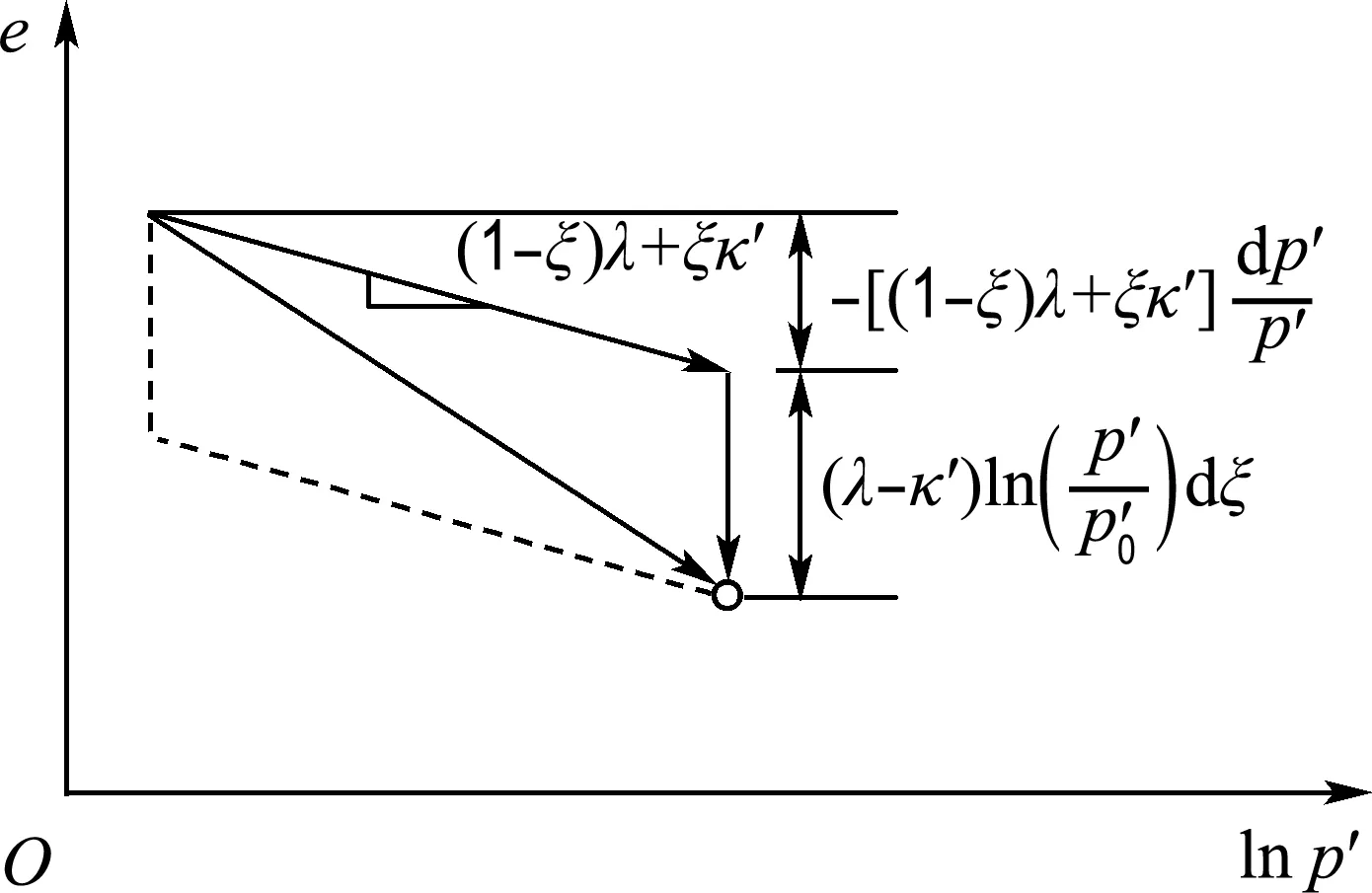
图3 结构性土的体变特性

1.3 结构性土的屈服应力

设某结构性土试样的初始状态应力为p′A，其初始孔隙比为eA，如图4所示．若对该试样进行压缩试验，则试样的压缩曲线将沿着图4中所示的弹性段(图4中点划线)发展，直至与结构性土的压缩曲线相交于点B，故点B处的孔隙比也可采用下式表示：

(9)

其中κ为结构性土弹性回弹曲线的斜率，假设该参数与土体的结构性无关，是一个恒定的常量．

由于点B又位于结构性土的压缩曲线上，故点B处的孔隙比还可采用式(7)计算，以下式表示：

(10)

联立式(9)、(10)，可得结构性土的屈服应力表达式为

(11)

式(11)表明结构性土的屈服应力与结构性因子相关，当土的结构性因子确定后可通过式(11)确定结构性土的屈服应力．

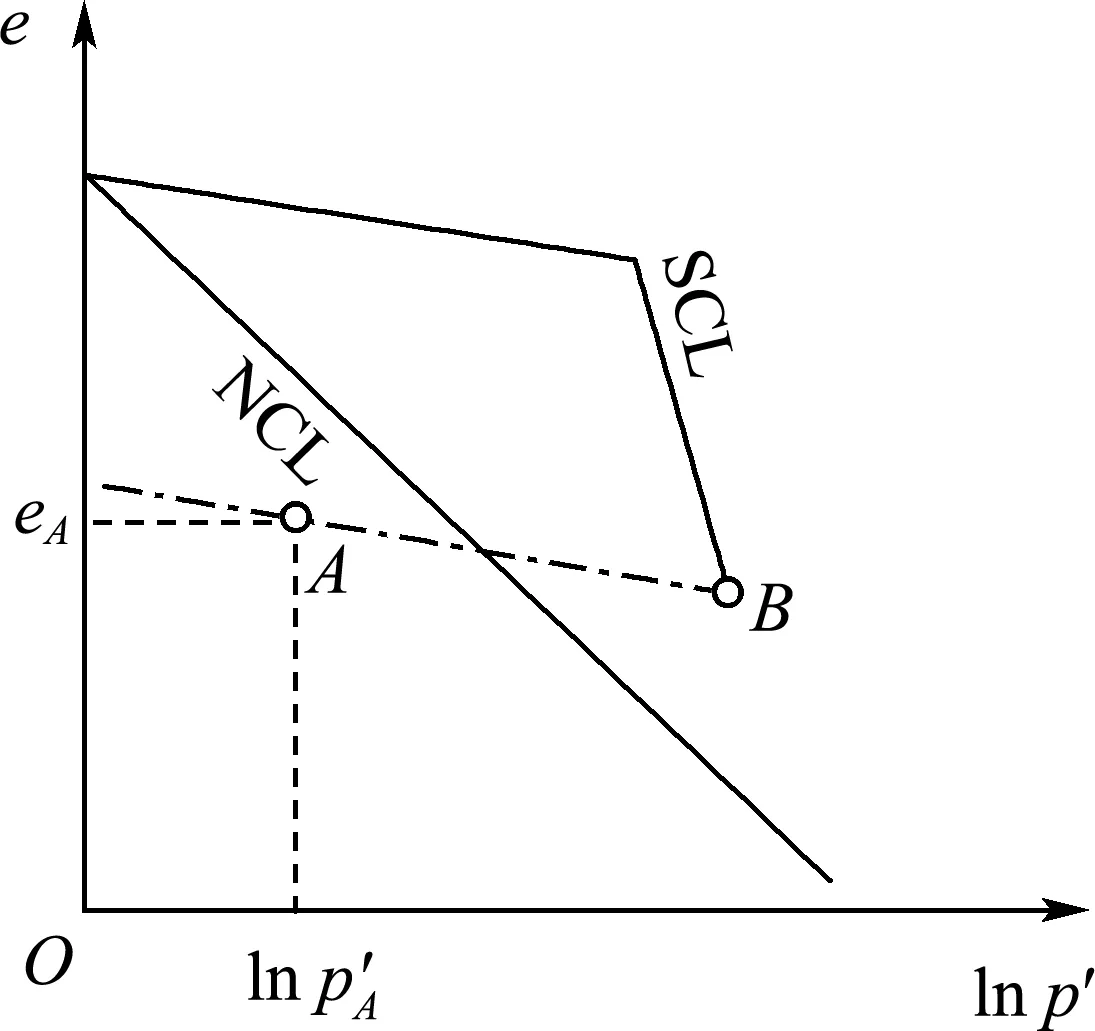
图4 结构性土的屈服应力

2 模型推导

2.1 结构性土的本构关系

土的总体应变由塑性体应变和弹性体应变组成，即

(12)

对于结构性土，其弹性体应变可表示为

(13)

结构性土在荷载作用下的总体应变可采用下式表示：

(14)

将式(13)、(14)代入式(12)，得到结构性土的塑性体应变为

(15)

对于重塑土的塑性体应变可采用相同的方法计算得到

(16)

其中p′c为重塑土的等效屈服应力，在该屈服应力下重塑土与结构性土的塑性体应变相等．将式(16)代入式(15)，得到结构性土屈服应力与重塑土等效屈服应力间的关系：

(17)

式(17)表明结构性土的屈服应力与结构性因子相关．设某土样的材料参数λ、κ和κ′分别为0.1、0.02和0.02，参考应力p′0为1 kPa，等效屈服应力分别为5、10、20、40、80和160 kPa，则结构性土的屈服应力与结构性因子间的关系如图5所示．当ξ为0时，土的结构性完全破坏，此时结构性土变为重塑土，因此结构性土的屈服应力与重塑土的屈服应力相等；当土样的结构性因子ξ变大时，表示土体的结构性增加，故结构性土的屈服应力也随之增加．

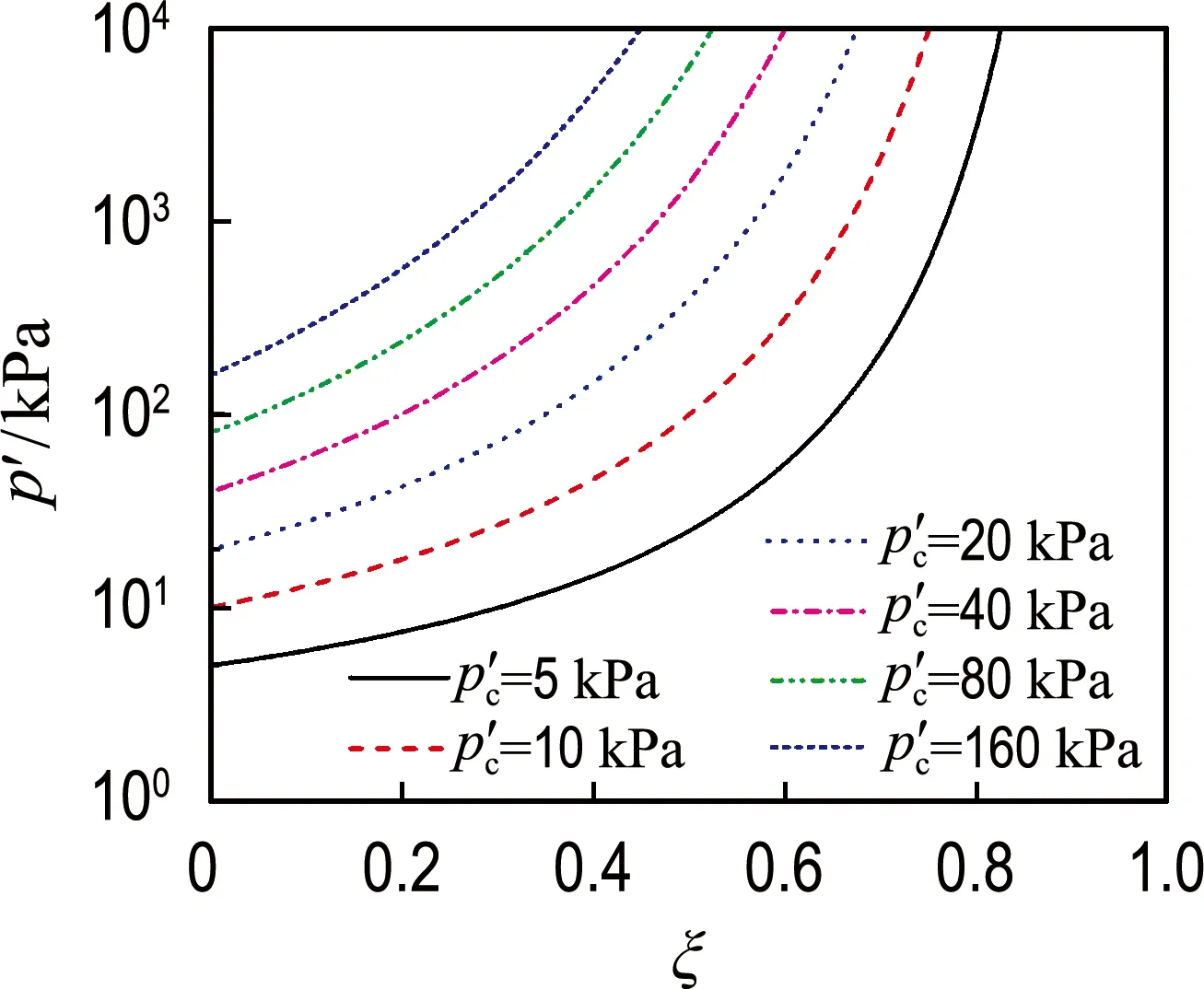
图5 结构性土屈服应力与结构性因子间的关系

结构性土的屈服面方程可采用修正剑桥模型[1]表示为

(18)

式中：q为广义剪应力，M为临界状态线的斜率，f为屈服面方程，p′x为屈服面与平均主应力轴交点处的平均主应力．将式(17)代入式(18)后，得到

(19)

将式(16)代入式(19)，整理后得到结构性土的屈服面和塑性势面方程：

(20)

根据协调方程的要求可知：

(21)

式中：σij为应力张量，i和j分别取1、2或3；Λ为塑性乘子．由式(21)可得塑性乘子的表达式：

(22)

2.2 结构性因子的发展准则

求解塑性乘子的关键在于确定结构性因子ξ的发展准则，结构性因子ξ表征了土体的结构性特征，当土体发生塑性变形时，土的结构发生破坏，结构性因子ξ降低，故结构性因子ξ为塑性应变函数，并随着塑性应变的增加而减小，可采用下式表示：

(23)

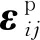
ξ(0)=1

(24)

ξ(∞)=0

(25)

设某3个结构性土试样的压缩曲线如图6所示，其屈服应力分别为图6点A、B和C对应的平均有效应力，由结构性因子ξ的定义可知点A、B和C的ξ值相等，但该组试样的屈服应力并不相同，故结构性因子ξ还需满足能够描述结构性强度对结构性因子ξ影响的条件．任何满足上述条件的发展准则都可作为结构性因子ξ的发展式．结构性在衰退的过程中伴随着塑性应变的增长，故可将结构性因子视为塑性体应变与塑性剪应变得到函数，并具有如下形式：

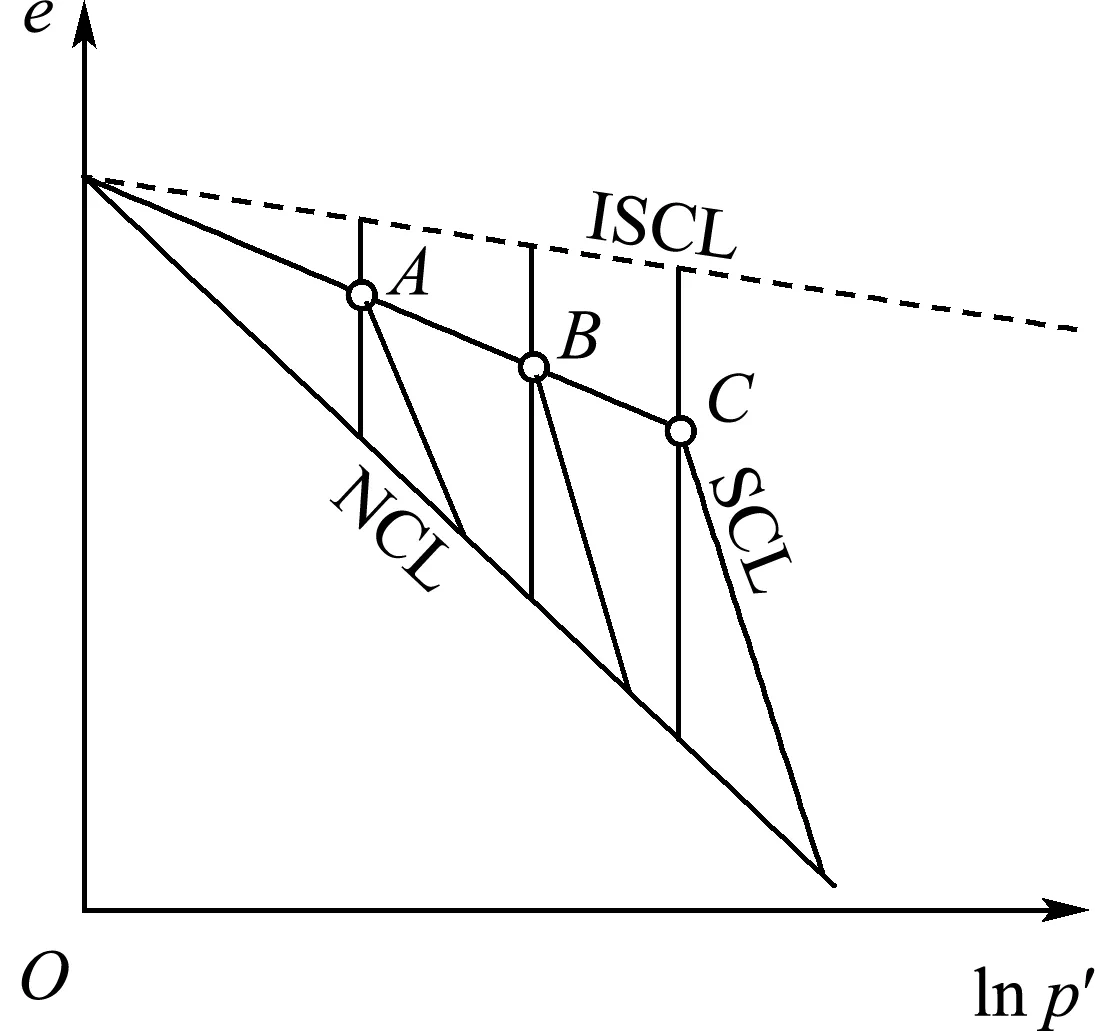
图6 结构性土的屈服特性

(26)

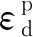
将式(26)表示为增量形式，得到结构性因子ξ的发展准则为

(27)

将式(27)代入式(22)后可得塑性乘子Λ的值，将塑性乘子Λ代入下式即可得到结构性土本构方程的增量形式：

(28)

式中：εkl为应变张量，Eijkl为结构性土的弹性模量，i、j、k和l分别取1、2或3．

3 模型验证

在本文所推导的结构性土的本构模型中共有8个参数，其中参数M、λ、κ和ν与修正剑桥模型的参数具有相同物理意义，且确定方法相同．κ′为结构性土本征压缩曲线的斜率，若根据试验数据无法得到结构性土的本征压缩曲线，κ′的值可取为土的回弹曲线的斜率κ．参数θ、m和md描述了结构性土在变形过程中土体结构的破坏规律，其值可通过对结构性土的三轴试验结果拟合得到．采用两种结构性土的试验数据与本文模型的预测数据进行对比，以验证本文模型的合理性．

Walker等[24]对取自地表下4.6 m处的Leda黏土进行了等应力比条件下的压缩试验，Leda黏土具有较强的结构性．本文采用该组试验数据验证所提本构模型．Leda黏土的压缩系数λ为0.25，弹性系数κ′和κ均为0.018，临界应力状态比M为1.2，泊松比ν取0.25．在压缩过程中应力比q/p′分别为0、0.63和1.00，压缩试验结果如图7所示．在采用本文模型计算结构性土的压缩曲线前还需确定结构性相关的土体材料参数θ、m和md，由于参数中含有与塑性剪应变相关的土体材料参数md，故本文采用应力比q/p′=1.00的试验数据拟合模型参数θ、m和md．采用Fortran 语言编写计算程序，将不同的θ、m和md值赋予土体材料，根据模型的计算结果，当材料参数θ、m和md分别为0.4、1.03和0.001时，模型预测结果与试验数据基本吻合，如图7所示，故结构性相关的土体材料参数θ、m和md分别取0.4、1.03和0.001．应力比q/p′分别为0和0.63 两组试样的模型预测结果如图7所示．试验结果表明，平均有效应力相等时，应力比越大的试样其孔隙比越小，这是由于在压缩过程中，剪切对土体中的结构产生破坏，故应力比越大的试样其孔隙比越小．根据模型预测结果和试验数据之间的对比可知，本文提出的模型能够较好地反映结构性土的压缩特性．

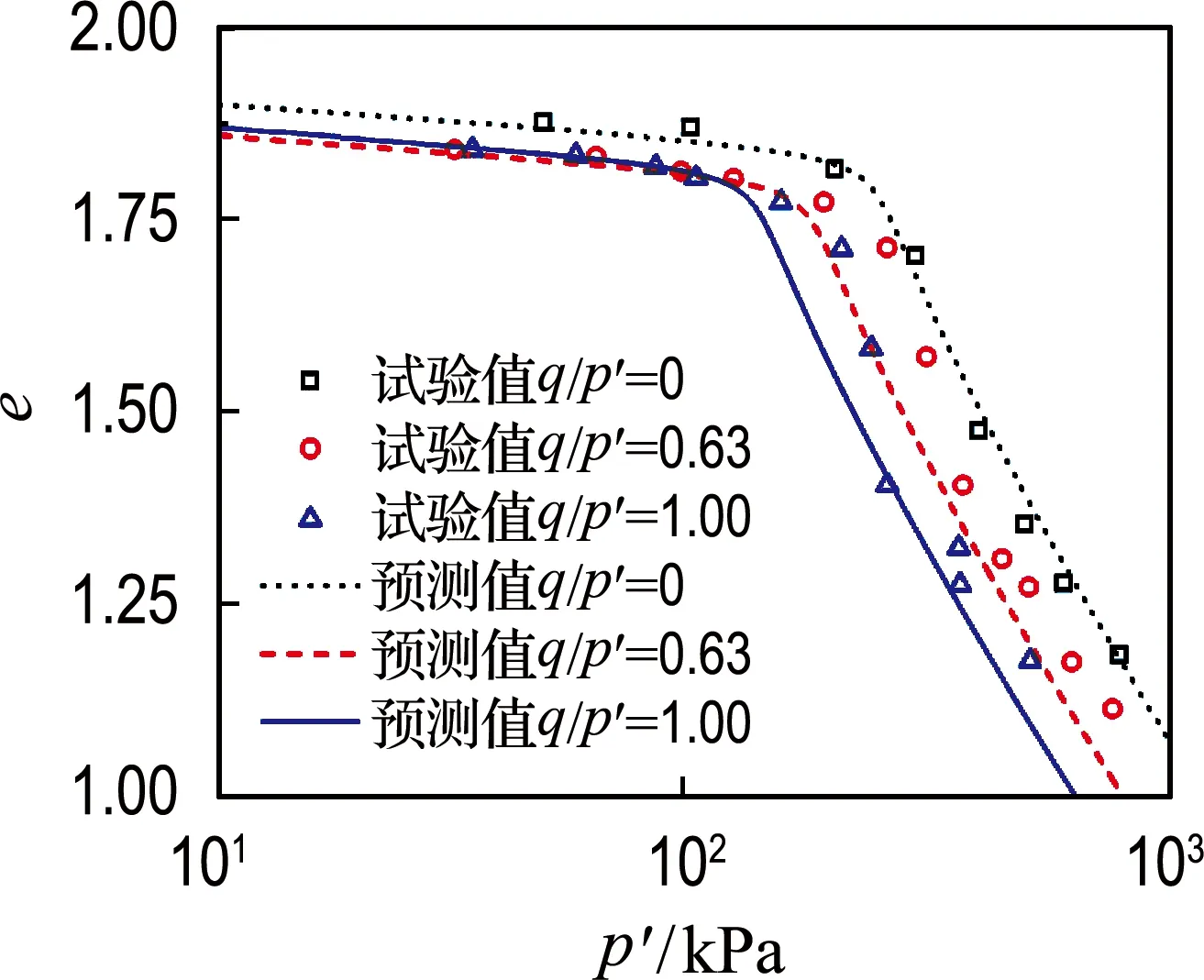
图7 等应力比条件下压缩试验结果与模型预测结果对比

Anagnostopoulos等[23]对科林斯运河泥灰土进行了三轴压缩试验，试样的压缩系数λ为0.04，弹性系数κ与κ′均为0.008，临界应力状态比M为1.32，泊松比ν取0.25．原状试样先分别各向等压固结至294、903、1 500和4 000 kPa，随后进行三轴排水剪切试验，试验结果如图8所示．以1 500 kPa围压条件下的试验数据拟合模型所需要的参数θ、m和md，根据模型的计算结果，模型参数θ、m和md分别为0.1、1.03和0.05时，模型预测结果与试验结果吻合度最高，如图8所示，故结构性相关的土体材料参数θ、m和md分别取0.1、1.03和0.05．在围压分别为294、903和4 000 kPa时，试样的数值计算结果如图8所示．由试验结果可知，随着围压的增大，应力-应变关系由应变软化变为应变硬化，试样的体变从体胀变为体缩．这是由于随着围压的增大，试样的结构性逐渐破坏，故试验曲线由应变软化变为应变硬化，体胀变为体缩．在高围压条件下，本文所提模型的预测结果与试验数据存在一定的差异，这可能与式(26)描述的土体结构衰退规律与实际的衰退规律还存在一定的区别有关，需要在后期研究中加深对结构性衰退规律的研究，以提高模型的计算精度．根据试验数据和模型预测结果的对比可知，本文提出的本构模型能较好地反映结构性土的应变软化和应变硬化特性，以及剪缩和剪胀等试验现象．

4 结 论

(1)根据结构性因子ξ推导得到的结构性土的体变方程表明：结构性土的体变由应力改变导致的体变和结构性破坏导致的体变两部分组成．

(2)结构性因子的发展准则是结构性土本构关系中的重要组成部分，文中给出了结构性因子发展准则需满足的3项原则，凡能够满足该3项原则的发展式，都可作为结构性因子的发展准则，可针对不同的结构性土建立不同的发展准则，故本模型具有较广的适用性．

(3)本模型中结构性对土体力学性质的影响是均匀连续变化的，当模型中的结构性因子ξ为0时，本模型退化为修正剑桥模型，避免了该点处数值计算结果的非连续性．