基于上下文多字典学习的高光谱波段选择

李 飞，卢 湖 川，薄 纯 娟

( 1.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024；2.沈阳航空航天大学 计算机学院，辽宁 沈阳 110136；3.大连民族大学 机电工程学院，辽宁 大连 116600 )

0 引 言

高光谱图像具有很高的光谱分辨率，包含数百个甚至上千个光谱波段．丰富的光谱信息为精确的目标识别和分类应用提供了有利条件[1]．然而，其庞大的数据也带来了数据传输与存储慢、冗余信息多等一系列问题，而且光谱维数的增加使传统图像处理方法不能完全适用于高光谱图像数据．一方面，高光谱图像中存在大量的冗余信息；另一方面，高光谱图像的光谱维数太高，很容易导致维度灾难问题[2-3]．因此，对高光谱图像进行降维处理是很有必要的．

针对高光谱图像的降维方法有两种：一种是特征提取，利用基于某一准则的变换矩阵进行数据变换得到低维光谱数据；另一种是波段选择(也称特征选择)，根据选择准则从原始波段挑选最佳波段子集，以保证光谱物理信息不被破坏．例如，主成分分析(principal component analysis，PCA)、线性判别分析(linear discriminant analysis，LDA)、非参数加权特征提取(non-parametric weighted feature extraction，NWFE)等，这些特征提取方法的处理结果改变了原始波段的物理意义．波段选择是高光谱图像在不进行特征变换的情况下降低波段维数的一种有效方法[4]．根据先验条件现有波段选择方法可以分为两类：有监督波段选择和无监督波段选择．有监督波段选择方法需要样本标签的先验信息，因此受到应用目标的限制[5]．例如，Wei等提出了基于粒子群优化的有监督波段选择算法[6]；Yang等根据各类别的谱特征，提出了采用序贯前向选择搜索方法选择波段[7]；Cao等将高光谱图像的局部空间信息集成到波段选择算法中[8]．与有监督波段选择方法不同，无监督波段选择不需要样本标签的先验信息，直接对无标签原始数据进行波段选择．虽然在某些特定的应用中，有监督波段选择方法获得的波段比无监督波段选择方法获得的波段更有效，但是在很多情况下先验知识不容易获得，因此无监督波段选择方法比有监督波段选择方法实用性更强，适用范围更广．例如，Bajcsy等对一些无监督波段选择方法进行了简要描述和实验，包括信息熵、一阶和二阶谱导数、比值、相关性和基于主成分分析的排序算法[5]．袁博等将相对熵矩阵与互信息结合，定量描述高光谱影像信息分布，进行波段选择[9]．Du等提出了基于相似性的波段选择算法：线性预测(linear prediction，LP)和正交子空间投影(orthogonal subspace projection，OSP)[10]．Yang等又利用GPU将LP和OSP算法与并行算法相结合，提高了运算效率[11]．Sui等提出了一种无监督的波段选择算法，将总体精度和冗余度的约束结合到波段选择过程中，设计了一个平衡参数通过优化模型来权衡总体精度和冗余度[12]．曾梦等使用深度对抗子空间聚类实现了高光谱波段选择[13]．

稀疏表示是对原始信号的分解过程，在这个过程中，将输入信号表示为字典的线性近似．在图像处理领域，稀疏表示已成功应用于图像去噪、图像复原、图像识别等领域．于伟等利用稀疏表示理论将上下文字典学习用于提高图像超分辨率技术[14]．同样，在高光谱图像处理方面，稀疏表示方法也取得了巨大的成功[15]．本文在多字典稀疏表示(multi-dictionary sparse representation，MDSR)波段选择算法[16]基础上，提出基于上下文多字典稀疏表示(context multi-dictionary sparse representation，CMDSR)波段选择算法．CMDSR波段选择算法将图像的每个波段看作字典原子，用该字典对相邻多个波段进行联合稀疏表示求解，可以得到代表输入样本原子和相关权重的稀疏向量．向量中的非零元素可以看成是这些波段在整个图像中所占权重，最后利用累计权重求出每个波段图像对于整个高光谱图像的贡献度，优先选择贡献度大的波段．为了评价该算法的性能，将该算法同几种无监督波段选择算法进行比较．采用一组藻类水体的高光谱曲线数据和一幅公开高光谱图像数据集做实验．

1 算 法

1.1 波段选择算法MDSR

波段选择的主要目的是找到一个最优或次优的波段子集，来代替原始高光谱图像信息．换句话说，这个波段子集在某些度量标准下能够近似表示原始数据．因此，应该找出每个波段对整个图像的贡献，根据贡献大小选择合适波段．稀疏表示可以用来计算波段对整个图像的贡献．当一个波段图像由其他波段图像组成的字典来近似线性组合时，所求出的稀疏系数可以表示每个字典原子对目标波段图像的贡献．如果系数绝对值较大，则该波段原子对目标波段的贡献较大；如果系数绝对值较小，则该波段原子对目标波段的贡献较小．通过相应的字典计算每个波段的稀疏表示，得到一系列权重．通过统计权重可以得到各波段对整个图像的贡献．因此，权重较大的波段就是最后选定的波段．

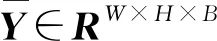
yi≈Diαi

(1)

这里字典矩阵Di包含除yi以外的其他波段，αi是线性组合的系数．这个公式也可以转换成如下形式：

yi=Diαi+βi

(2)

其中βi是误差项．如果αi是稀疏的，那么可以计算出αi的值．可以将其看成是Di中每个原子对波段yi的贡献情况，系数越大，该原子对这个波段的贡献越大，反之亦然．稀疏系数αi可以通过求解下面的约束优化问题得到：

(3)

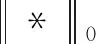
(4)

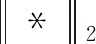
(5)

其中K0是给定稀疏度的上界．可以用贪婪追踪算法近似求解，例如，匹配追踪(matching pursuit，MP)算法、正交匹配追踪(orthogonal matching pursuit，OMP)算法、子空间追踪(subspace pursuit，SP)算法．这里采用OMP算法求解[17]．MP算法的基本思想是：通过从字典矩阵中选择与信号匹配的原子来构造稀疏近似．通过推导信号的残差，选择与残差匹配最佳的原子．重复上述过程，直到残差可以忽略或达到预先定义的迭代次数．OMP算法在MP算法基础上做了改进，要求在分解每一步选择的所有原子都是正交的．在相同的准确度条件下，OMP算法的收敛速度比MP算法快．

每个波段图像由相应的字典表示之后，得到一个稀疏系数矩阵．在该矩阵中，大多数系数都为零．系数的绝对值越大，对应的字典原子对原始高光谱图像贡献越大．对整个系数矩阵，按行计算不为零的系数个数，得到一个横坐标为波段标号的直方图．如果用hi表示直方图，那么计算公式如下：

(6)

当x=0时，g(x)=0，其他情况下g(x)=1．在直方图中，对系列进行排序，最后选系列值较大的波段．下面给出具体的算法步骤．

步骤1将高光谱图像拉伸成二维矩阵．

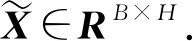
步骤5用式(6)统计非零元素系数个数．

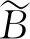
1.2 波段选择算法CMDSR

高光谱图像中，相邻元素的光谱具有很高的相似性[18]，同理，相邻波段通常也具有相似的空间信息，因此在上文提出的稀疏表示模型中，应该考虑上下文波段信息，整体流程如图1所示．对于给定的字典，小范围内邻域波段的稀疏性相似，是相同公共原子的稀疏线性组合，只是对应的稀疏系数不同．例如yi和yj是两个相邻的波段图像，那么yi对字典的稀疏表示为

yi=Dαi=αi，λ1dλ1+αi，λ2dλ2+…+αi，λkdλk

(7)

这里下标集Λk={λ1，λ2，…，λk}对应字典原子的下标．yj与yi相邻，那么支撑yj的原子集与支撑yi的原子集相同，可用{dv}v∈Λk表示，但是对应的系数集{αj，v}v∈Λk不同，即：

yj=Dαj=αj，λ1dλ1+αj，λ2dλ2+…+αj，λkdλk

(8)

由此可以扩展到一个包含多个相邻波段的邻域情况，例如，Y=(y1y2…yN)表示一个B×N的矩阵，列向量{yn}n=1，2，…，N是其中的一个波段，可以用联合稀疏表示：

Y=(y1y2…yN)=

(Dα1Dα2…DαN)=

D(α1α2…αN)=DS

(9)

这里S=(α1α2…αN)，它是一个行稀疏矩阵，在给定字典D的情况下，可以通过解决下面的联合稀疏问题求解：

(10)

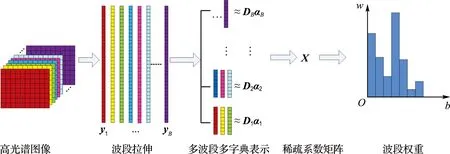
图1 本文提出的波段选择算法总体流程图

上面的公式也可以改写成

(11)

步骤1将高光谱图像拉伸成二维矩阵．

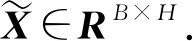
步骤5用式(6)统计非零元素系数个数．

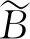
2 实验结果与分析

在实验中，将本文算法与4种波段选择算法做比较，分别是MDSR算法、LP算法、OSP算法和Cluster(基于聚类的波段选择)算法．

2.1 数据描述

本实验采用两组数据集，第1组是藻类水体高光谱数据，来自中国海洋监控中心遥感实验室.它是4类藻种水体在不同叶绿素浓度下的光谱反射率曲线，包括甲藻、叉角藻、夜光藻和异弯藻．光谱值包含240个波段，波长覆盖范围为400～1 000 nm．第2组数据ROSIS高光谱图像PaviaU 采集自意大利北部的帕维亚大学校园，共有103个波段，610×340个像元，包含9类地物．

2.2 波段选择结果

MDSR和CMDSR两个算法中，创建的字典要保证过完备性，但是高光谱图像拉伸成二维矩阵后，维数过大，因此要减少字典的原子维数．在文献[16]和本文中均采用随机选取N个像元的方法，文献[16]验证了N值的变化不会影响波段选择的结果和性能．图2展示MDSR和CMDSR算法对两组数据集的波段选择结果．横坐标为波段序号，纵坐标是波段权重．权重值越大，说明该波段对整个数据的贡献越多．CMDSR算法的处理结果与MDSR算法的处理结果基本一致，但是在时间效率上考虑，CMDSR算法效果更好．

2.3 性能分析

为了分析波段选择算法的性能，从分类精度、波段相关性和算法运行时间3个方面与其他波段选择算法进行比较和分析．

(1)分类精度

采用KNN方法对波段选择后的藻类水体数据和PaviaU数据进行分类．在藻类水体高光谱分类实验中，每类选3个样本；在PaviaU高光谱图像分类实验中，每类选20个样本．波段数量从1到50．在MDSR和CMDSR方法的实现过程中，稀疏度设置为6．在KNN方法实现过程中，最近邻值分别设置为4和6．为了减少随机性，每个结果都经过10次运行后求得平均值．图3表示了两组数据的整体分类精度．横坐标为波段数量B，纵坐标为总体分类精度p．由于藻类水体数据每类样本数量较少，精度变化差异较大，在波段数量超过30之后，MDSR和CMDSR表现了较好的效果．在PaviaU数据上，各个算法所得分类精度相差不多，都比较平稳，但整体来说MDSR和CMDSR算法优于其他算法，而基于聚类的算法稍显落后．

(2)相关系数

为了衡量所选波段的可分性，计算了不同算法所选波段的相关系数．一般来说，所选波段之间的相关性越低越好．图4显示了波段之间的相关性随波段数目的变化情况．横坐标为波段数量，纵坐标为波段间相关系数c．除了OSP算法外，其他几种算法的波段选择结果都显示了比较低的相关性，尤其在波段数量比较少时，CMDSR算法体现了很好的性能．

(3)运行时间

为了评估该算法的效率，计算了每种算法的运行时间．所有比较的算法都在Matlab 2016中实现，并在8 GB内存，Intel Core i5-2400 CPU的运行环境下进行测试．图5显示了不同波段选择算法在波段数目不同时的运行时间．横坐标为波段数量，纵坐标为算法运行时间．结果表明，基于聚类的算法耗时最少．虽然本文算法不是最快的，但是它与大多数算法比较，效率比较高，更重要的是，本文提出的算法几乎不受波段数量的影响，而LP和OSP算法随着波段数量的增加运行耗时越来越长．由于CMDSR算法计算的迭代次数明显比MDSR算法少，因此在运行时间上更有优势．

3 结 语

本文提出的高光谱图像波段选择算法，很好地保留了原始图像某些波段的物理信息．与目前流行的几种波段选择算法比较，在分类精度上可以达到或超过其他同类算法，在相关性和运行时间上表现出更大的优势．本文不但在公开数据集上，而且在一组藻类水体高光谱数据集上验证了所提算法的可行性．