基于状态空间的轮系分析统一数字模型

邱 俊，王 德 伦，马 雅 丽

( 大连理工大学 机械工程学院, 辽宁 大连 116024 )

0 引 言

在齿轮箱的设计过程中，设计者根据给定的工况条件进行齿轮传动方案的设计，通常情况下会得到很多轮系方案．为了确定传动轮系的最佳设计方案，需要对轮系进行分析，但对于构型复杂的轮系，采用一般传动链的传统运动学分析方法[1-3]难以高效率地完成大量设计方案分析比较．究其原因是未针对任意轮系建立统一的数字模型，计算机无法实现对轮系方案的快速识别与分析．

为此，国内外学者采用多种方法针对复杂轮系分析进行了研究．基于轮系单元的轮系运动学分析方法[1-6]，将周转轮系分解成若干个基本周转轮系或轮系单元组的轮系单元进行分析，但缺少对基本单元的定义和基本单元内部联系的讨论．利用图论画出表示轮系构件连接关系的拓扑图[7-9]或者离散图[10]表示轮系构件连接关系，建立轮系分析模型可以对轮系运动传递有直观的认识．而王德伦等[11]借鉴机械设计的矩阵分解方法以及控制理论中的状态空间概念建立了机械运动变换状态空间表示方法，文献[12-15]在其基础上对并联、混联以及多自由度机构建模进行了研究，但是复杂轮系结构复杂，易形成多环运动和动力传递路径，在分析上具有特殊性．本文针对复杂轮系运动、动力、结构等多元特征，借鉴基于机构变换单元的状态空间方法建立轮系统一数字模型，通过编程实现对任意复杂轮系的数字化识别与分析．

1 轮系基本单元状态变换方程

1.1 轮系基本单元

齿轮传动实现了由输入轴到输出轴的运动特征、动力特征、结构特征(空间方位)的传递与改变．任意一个复杂的轮系传动都可以看成内啮合和外啮合轮系传动单元的组合，因此有：

定义1将一对外啮合或内啮合齿轮传动机构定义为轮系基本单元．

组成轮系基本单元的构件称为基本构件，为统一表达和利于数字化编程，用数字编号代表基本构件，如图1所示．若机架与非机架基本构件相固结，则形成单自由度基本单元；若机架为单独的基本构件，则形成两自由度基本单元．

轮系中基本构件的状态特征可以由运动、动力、结构特征构成[11]，而轮系基本单元承担着轮系中最基本的功能——将输入构件状态特征转换为输出构件的状态特征．本文提出利用输入、输出特征矢量与特征矢量变换方程来描述轮系基本单元的功能与性质，采用向量-矩阵-方程的表达策略实现基本单元输入、输出特征状态转换关系，探讨输入、输出构件变换、机架变换等基本单元变换规律，建立基本单元之间典型的邻接关系，通过计算机编程，形成任意复杂轮系转速、转矩、功率流等数字化分析方法．

1 太阳轮；2 行星轮；3 内齿圈；4 行星架；5 机架

1.2 轮系坐标系

为清楚地表达轮系中基本单元、基本构件之间空间位置的关系，建立轮系基本单元坐标系(O-XYZ)、轮系基本构件坐标系(o-xyz)，如图2所示．

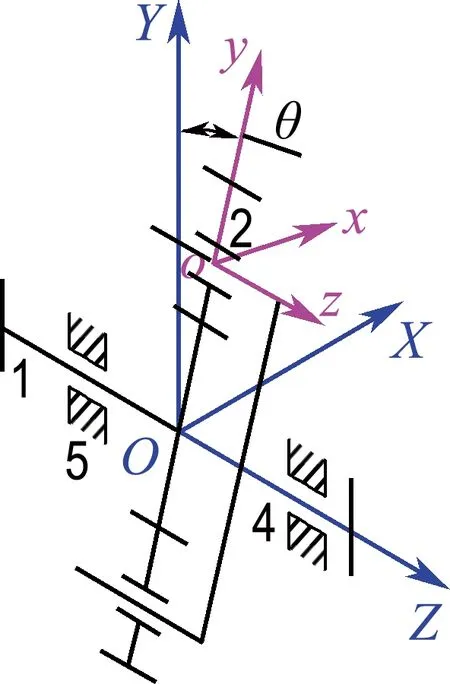
图2 轮系坐标系

(1)轮系基本单元坐标系(O-XYZ)

坐标系固定在基本单元机架上，以基本单元回转中心(太阳轮、内齿圈、行星架回转中心、行星轮公转回转中心)为原点，以回转中心轴向为Z轴方向，X轴方向垂直于机架平面，Y轴方向垂直于XOZ平面．

(2)轮系基本构件坐标系(o-xyz)

坐标系固定在基本构件上，以基本构件回转中心为原点，以回转中心轴向为z轴方向，x轴方向垂直于构件平面，y轴方向垂直于xoz平面．

通过坐标变换就可以实现任意轮系基本构件的空间方位矢量在整体坐标系下的变换，并可以写出基本构件特征矢量在整体坐标系下的确切表达．

1.3 状态变换方程

输入、输出构件的状态特征可以由表达基本构件运动、动力和结构特征(方位)状态的最小数目的变量有序集合进行表示，通常用轮系中构件的转速、转矩以及构件方位矢量来描述，写成多维矢量的形式，输入状态特征矢量Ri和输出状态特征矢量Ro分别表示为

(1)

(2)

式中：ωi、ωo分别为输入、输出构件的转速矢量；Mi、Mo分别为输入、输出构件的转矩矢量；ri、ro分别为输入、输出构件的方位矢量．

通过轮系基本单元可以建立输入、输出构件状态特征矢量的变换关系，可以写成矩阵形式，称为特征矢量变换矩阵A．轮系基本单元输入、输出状态特征矢量变换关系可以表示为

Ro=A·Ri

(3)

其中A为n×n矩阵，n为Ri、Ro的维数．

定义2式Ro=A·Ri表达了轮系基本单元的输入、输出状态特征矢量的变换关系，称为基本单元特征矢量状态变换方程，简称状态变换方程．

1.4 轮系基本单元状态变换矩阵

对于单自由度轮系单元，一个输入特征矢量，一个输出特征矢量，轮系状态变换方程如式(3)所示．对于两自由度基本单元，两个输入特征矢量，一个输出特征矢量，轮系状态变换方程表示为

Ro=A1·Ri1⊕A2·Ri2

(4)

其中矩阵Aj(j=1、2)描述特征矢量中各变量之间的关系，称为特征矢量变换矩阵；符号⊕为状态特征矢量相加符号．

单自由度轮系单元转速、转矩、方位由输入构件到输出构件的状态变换方程基本形式为

(5)

两自由度轮系单元具有两个输入构件，一个输出构件，因此两自由度轮系单元状态矢量变换方程的基本形式为

(6)

式(5)、(6)中λj1、λj2、λj3(j=1、2)分别为特征矢量变换矩阵Aj(j=1、2)中转速、转矩、方位矢量的变换子矩阵．在基本单元坐标系下，任意构件特征矢量中的转速、转矩、方位矢量可以分解为坐标上的投影：

状态特征矢量相加运算的条件：两状态特征矢量相加需要满足空间方位矢量相同．两状态特征矢量相加是对于同一单元中同一构件而言的，相加的结果矢量中的转速和转矩分别为两状态特征矢量中转速和转矩对应分量之和，结果矢量的空间方位坐标不变．

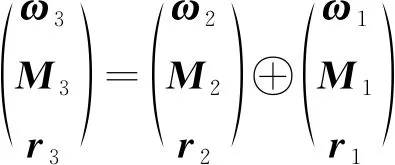
ω3=ω2+ω1

M3=M2+M1

r3=r2=r1

2 轮系基本单元的变换

齿轮基本单元作为一般机构运动链，可以进行输入、输出变换(图3)和机架变换(图4)，而对应的输入构件、输出构件的运动、动力、结构特征状态随之改变．

任何复杂轮系都是由内啮合和外啮合轮系基本单元通过输入、输出变换和机架变换后，按照一定的规律互相邻接形成的．图3(a)所示两自由度轮系单元的状态变换方程为

R2=A1·R1⊕A2·R4

(7)

根据转速、转矩、方位矢量的变换规律可推导Aj(j=1、2)是可逆的，因此可以得到图3(b)所示两自由度轮系单元的状态变换方程为

(8)

将基本构件4-行星架与5-机架固定，可以得到如图4(b)所示单自由度轮系单元的状态变换方程为

(9)

其中F为表示基本构件与机架固定的位运算，将R4中的转速分量ω置零，因转矩是通过转速比表达，进一步可以得到

(10)

式(7)～(10)实现了轮系基本单元输入、输出变换，机架变换的数学表达，轮系基本单元特征矢量通过一定的运算规律可以得到任意的轮系单元，这些运算规律将用于轮系分析中，实现轮系单元的数字化识别．

3 轮系单元间的邻接数学模型

3.1 轮系单元间的邻接关系

任何复杂轮系都是由轮系单元按照一定规律邻接构成的，为了方便表述，用带箭头的线段和框图来表示轮系单元．经分析，发现任意两个轮系单元存在串联邻接与并联邻接两种典型邻接关系．图5(a)所示轮系单元串联邻接关系，其特点为前置单元的输出构件与后置单元的输入构件合并，状态特征矢量通过合并的基本构件进行传递；图5(b)所示轮系单元并联邻接关系，其特点为两个轮系单元的输入或输出基本构件合并，状态特征矢量通过合并的基本构件进行传递．

轮系单元邻接会导致基本构件的合并，引起轮系传动链自由度的变化．若两个轮系单元邻接，其自由度满足以下关系：

D=D1+D2-N

(11)

其中D为两个轮系单元邻接组成轮系的自由度；D1和D2分别为两个轮系单元的自由度；N为合并构件数目．

考虑轮系单元自由度的约束，两个轮系单元邻接关系如表1所示．

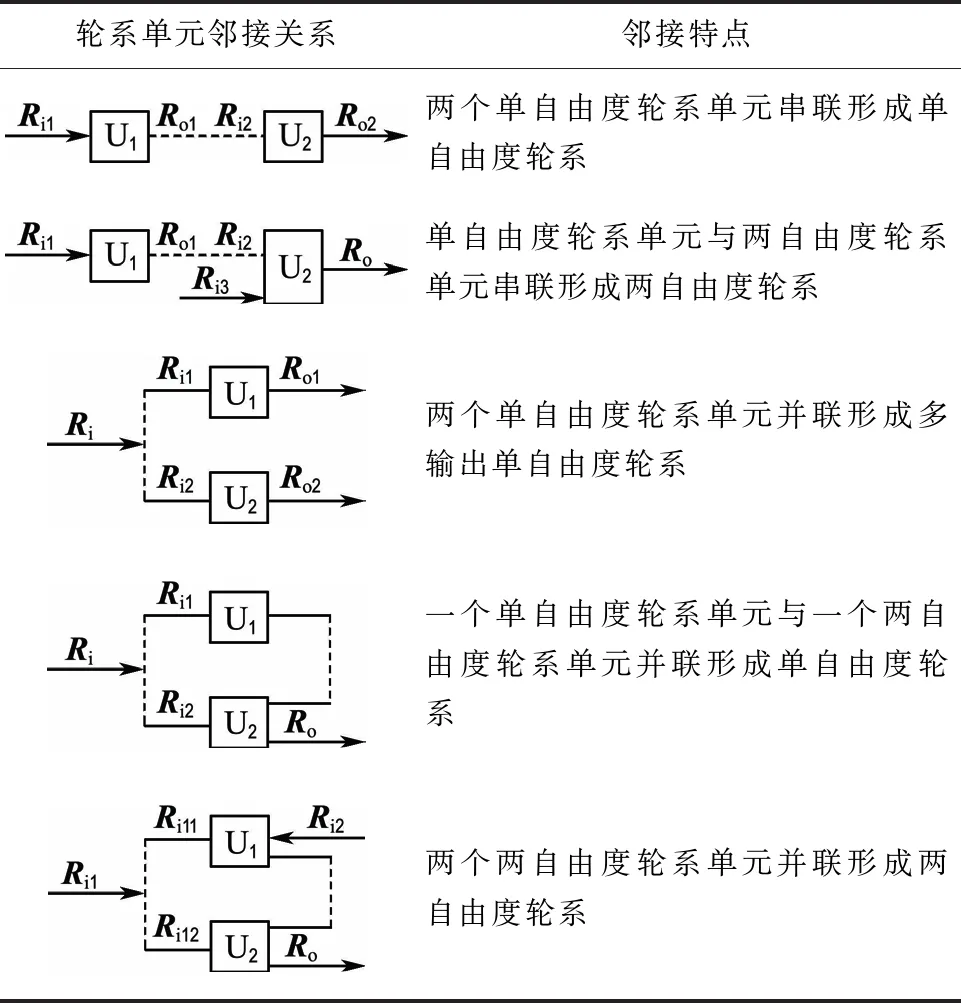
表1 两个轮系单元邻接关系

3.2 轮系单元间邻接关系矩阵

两个轮系单元邻接，基本构件的转速、转矩、方位矢量需要满足邻接规律．两轮系单元串联邻接时，讨论的是前置单元输出构件状态特征矢量Ro1与后置单元输入构件的状态特征矢量Ri2之间的关系；两轮系单元并联邻接时，讨论的是两并列单元输入(或输出)Ri1与Ri2状态特征矢量与合并的基本构件状态特征矢量Ri之间的关系．

(1)转速矢量

两轮系单元串联或者并联邻接，合并的两个基本构件转速矢量必须相同，即两个基本构件的转速大小和方向相同．

(2)转矩矢量

两轮系单元串联或者并联邻接，合并的两个基本构件转矩满足

Mik=t·M

(12)

式中：Mik为合并构件的转矩矢量；M为输入或输出的转矩矢量；t为转矩分配系数矩阵，是对角阵，根据同一构件转矩平衡可知，矩阵参数tk满足

对于两自由度轮系单元求解转矩时需要利用相对运动原理(即反转法)附加补充方程．

(3)方位矢量

两轮系单元串联或者并联邻接，合并的两个基本构件方位矢量必须相同．

根据以上基本构件邻接规律，可以得到两轮系单元串联邻接(图5(a))，前置单元输出矢量与后置单元输入矢量之间转换关系的数学表达如下：

Ri2=C·Ro1

(13)

式中：C为轮系单元串联邻接矩阵；Ro1为前置单元输出矢量；Ri2为后置单元输入矢量．

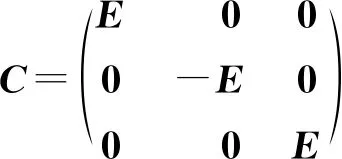
其中E为单位阵．

两轮系单元并联邻接(图5(b))，总输入、输出矢量与两轮系单元输入、输出矢量之间的转换关系的数学表达如下：

Ri1=G1·Ri，Ri2=G2·Ri

(14)

式中：G1、G2为轮系单元并联邻接矩阵；Ri为总输入矢量；Ri1、Ri2为两轮系单元输入矢量．

3.3 复杂轮系拆分

基于轮系基本单元与轮系状态空间的轮系分析方法，需要将原轮系拆分成轮系基本单元的形式．轮系拆分成基本单元的规则：轮系中一对齿轮啮合对应一个轮系基本单元．例如对图6所示差动轮系进行拆分，可以得到图7由4个轮系基本单元组成的轮系．

为清楚地表达拆分成基本单元的轮系，采用状态矢量变换框图(图8)的形式进行表达．

在状态矢量变换框图中各符号意义为：Ri、Ro分别代表轮系的输入、输出的状态矢量；Rmn代表单元的状态矢量，U-m表示轮系单元，其中m为单元编号，n为基本构件编号；Cab表示轮系单元串联邻接，a为前置单元编号，b为后置单元编号；Gq表示轮系单元并联邻接矩阵，q为并联邻接序号．

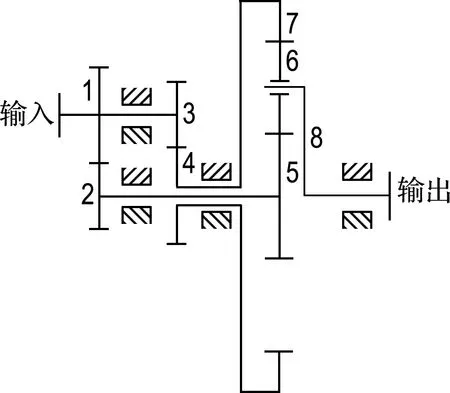
图6 差动轮系

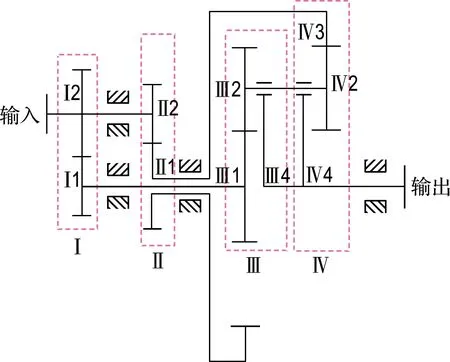
图7 差动轮系的拆分

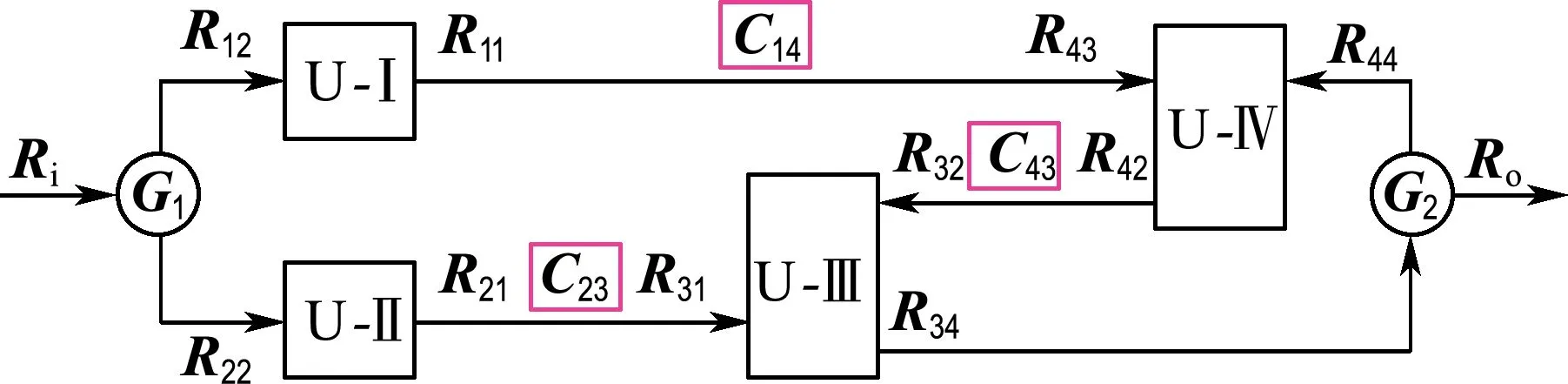
图8 差动轮系矢量变换框图

4 轮系状态空间及其性质

定义3所有轮系单元对应的状态特征矢量的集合称为轮系特征矢量状态空间，简称轮系状态空间．

在轮系状态空间中，一个轮系单元总可以找到成对的状态特征矢量(单自由度轮系单元)或者3个状态特征矢量(两自由度轮系单元)与之对应，分别称为两对偶矢量和三对偶矢量，统称为对偶矢量．轮系单元、对偶矢量、变换矩阵三者是一一对应的．式(1)、(2)中输入、输出特征矢量是任意的，满足加法和乘法矢量运算，这是形成矢量空间的基本条件，但状态特征矢量描述的是基本构件的物理状态，因此形成的矢量空间具有特殊性．状态特征矢量在轮系状态空间中总是以输入、输出对偶的形式出现，两对偶矢量可以表示为RiRo，三对偶矢量可以表示为Ri1Ri2Ro．

设BiBo、CiCo、DiDo、EiEo、BiCiDo属于轮系状态空间Ω，则有如下性质：

(1)加法

BiBo⊕CiCo=BiCiDo

其中Bo、Co、Do满足状态特征矢量相加运算条件，该性质为两自由度轮系单元的状态特征矢量之间的运算规律．

(2)加法交换律

BiBo⊕CiCo=CiCo⊕BiBo

该性质说明两自由度轮系单元的两个输入状态特征矢量的地位是同等的．

(3)乘法

BiBo·CiCo=BiCo

该性质表明了两个串联轮系单元的状态特征矢量之间的运算规律．

(4)乘法结合律

BiBo·CiCo·DiDo=BiBo·(CiCo·DiDo)

(5)乘法交换律

BiBo·CiCo=CiCo·BiBo

性质(4)和(5)表明两个轮系单元串联，前后位置基本单元的地位一致．

(6)乘法分配率

BiBo·(CiCo⊕DiDo)=BiBo·CiCo⊕BiBo·DiDo

该性质表明了串并联复杂轮系的状态特征矢量的运算规律．

(7)数乘

α是常量，α·BiBo∈Ω．

该性质表明使对偶矢量的数值扩大或缩小，并不改变对偶矢量的性质，对偶矢量代表轮系单元的固有属性．

(8)可逆

该性质表明输入、输出状态特征矢量的可逆性，说明了轮系状态特征的可逆性．

以上运算性质说明轮系状态特征矢量构成了一个特殊的线性空间，利用这些运算性质可以实现轮系单元的自由组合，形成串联、并联、反馈不同形式的轮系，可以将复杂的轮系结构进行解构，清楚地表达多环运动和动力传递路径，对进行轮系分析以及形成轮系设计中轮系单元状态特征矢量的运算奠定了基础．

5 轮系分析的状态空间方法

将复杂轮系拆分成轮系基本单元，由轮系基本单元变换得到轮系单元的状态矢量变换矩阵，根据轮系单元间邻接关系建立状态矢量变换方程组并进行求解，就是轮系分析的过程．根据状态矢量变换矩阵分解规则，将轮系总体状态矢量变换矩阵分解成子矩阵，将子矩阵对应的轮系单元按照一定的组合规律进行组合，形成不同的轮系方案，就是轮系设计的过程[16]．

复杂轮系分析的状态空间方法流程为：首先按照轮系拆分规则对原轮系进行拆分，得到由基本单元组成的轮系，根据轮系基本单元的变换运算规律得到轮系中对应的轮系单元；根据单元间的邻接关系形成状态矢量变换方程，将状态矢量变换方程写成基本单元状态变换矩阵的形式，通过编程对方程组进行求解，得到每个构件的转速、转矩，进而得到每个构件传递的功率以及功率的传递方向．现以一个复杂轮系(图9)为例，利用轮系分析的状态空间方法对其进行分析．

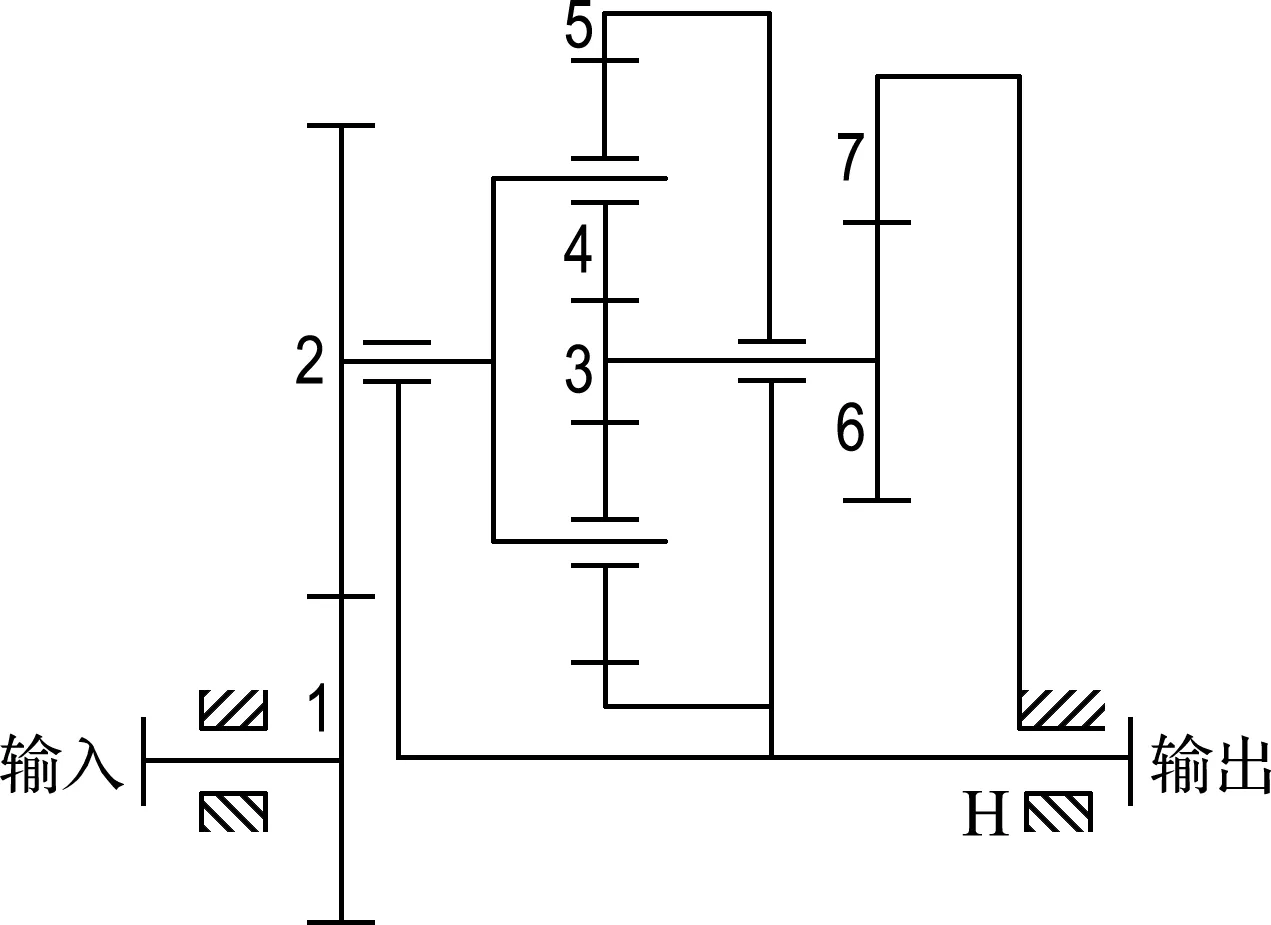
图9 复杂轮系

各齿轮的齿数分别为z1=24、z2=60、z3=17、z4=20、z5=57、z6=22、z7=72，轮系输入转速为15 r/min，输入转矩为100 N·m，求解轮系各构件的转速、转矩，并分析轮系中功率流向．

(1)按照轮系中一对齿轮啮合对应一个轮系单元的拆分规则，将复杂轮系拆分成轮系单元的形式，得到如图10所示轮系，共得到4个轮系基本单元．

(2)对于如图10所示的轮系单元都可以由轮系基本单元通过机架变换和输入、输出变换得到，即通过确定轮系基本单元输入、输出构件以及机架就可以通过状态矢量运算得到对应轮系单元的状态变换方程，通过编程可以实现复杂轮系的数字化识别与表达，得到以下方程组：

图10 复杂轮系拆分

输出矢量

Ro=G32·G22·R44

(3)对应以上状态矢量变换方程，根据各个轮系单元状态变换矩阵，识别单元之间的邻接关系，自动得到轮系单元间邻接矩阵．

(4)采用高斯消去法与牛顿迭代法共同求解构成的非齐次线性方程组，可以得到轮系各个构件的转速与转矩(见表2)．由转矩和转速可以求得通过每个构件的功率，功率为正值，则为输入功率，流入单元；功率为负值，则为输出功率，流出单元．根据计算结果画出功率实际流向，如图11所示．

根据以上案例可以得出结论，基于状态空间的轮系分析统一数字模型，可以将复杂的轮系结构进行解构，清楚地表达多环运动和动力传递路径，可以实现对任意复杂轮系的数字化识别与自动化分析．

表2 轮系分析结果

图11 轮系功率流向图

6 结 论

(1)轮系基本单元状态特征矢量及状态变换方程能够准确地描述轮系基本单元的运动特征、动力特征、结构特征的传递变换关系，是建立轮系分析统一数字模型的基础．

(2)轮系基本单元输入、输出对偶矢量构成轮系状态空间，对偶矢量运算规则揭示了轮系基本单元变换规律以及单元之间的邻接关系，共同决定了轮系状态空间的性质，为轮系分析建立统一的数字模型提供了理论基础．

(3)本文提供了一种任意复杂轮系数字化识别与分析的数字模型，为轮系方案设计阶段大量构型分析提供了运动、动力以及功率流快速、准确的数字化分析方法．