小天体不规则度与光学导航质心提取及应用

崔平远，贾 贺，朱圣英

(1. 北京理工大学深空探测技术研究所，北京 100081；2. 深空自主导航与控制工信部重点实验室，北京 100081；3. 飞行器动力学与控制教育部重点实验室，北京 100081)

0 引 言

小天体探测具有重要的科学价值，是近些年世界各国深空探测的热点问题。自主导航与控制系统是成功实现小天体近距离探测任务的前提和保证[1-2]。光学导航(OPNAV)凭借自主性强、精度高等优点，在深空探测自主导航方面已经有了广泛应用[3-4]。小天体探测一般通过拍摄目标天体图像，然后提取目标天体的形心或光心，以形心和光心代替质心得到相机至天体质心的视线(LOS)信息进行导航[5-6]。不规则小天体不同的成像特点对小天体形心/光心提取精度有很大影响，而小天体形心/光心提取的精度直接影响到自主光学导航的精度，所以高精度的形心/光心提取算法是至关重要的。

针对形心提取问题，Christian等[7-8]提出了一种目标天体形心和视直径(CAD)的图像处理算法，首先利用椭圆和圆拟合算法求取目标形心，得到视线方向，然后利用目标天体的形状模型和投影图像进行比对得到视直径信息。但是提前获得小天体形状和尺寸的精确模型是很困难的，另外由于小天体形状不规则，导致在相机像平面的投影不规则，所以很难将投影图和实际模型进行对比分析。基于天体边缘进行椭圆拟合是实现形心提取的主要方法。常用的椭圆拟合方法主要有3类，一类是基于HOUGH变换的椭圆拟合方法[9]，另一类方法是基于不变矩的方法[10]，再一类则是基于最小二乘的拟合方法[11]。椭圆拟合方法仅适用于真实天体边缘近似规则椭圆的情况，当天体边缘不规则时，则会存在较大误差，造成椭圆拟合的误匹配，从而得到误差较大的天体形心位置坐标。

针对光心提取问题。高斯拟合法及其改进算法是近些年较为常用的光心提取方法[12-13]，包括基于不饱和点的高斯曲面拟合法[14]，利用一阶导数零交叉点的方法确定峰值像素坐标分布后利用高斯拟合法求解等[15]。在理想情况下，光斑的强度分布应该符合高斯分布，所以高斯曲面拟合法提取精确度高。然而当亮点的强度分布为非高斯的情况则精度较差，此时只能选用灰度重心法提取小天体的光心。该方法通过在一个预先确定的图像子区域内提取超过亮度阈值的所有像素，来确定该区域的亮度中心，该方法简单快速，但提取精度有限。

针对以上问题，考虑到不规则小天体不同的成像特点对图像处理算法的提取精度影响很大，因此需要对小天体的不规则程度进行判断，评价拟合精度，分布特性等指标，进而选取最合适的拟合方法。本文提出了一种小天体不规则度定义方法。小天体不规则度可以表示小天体的不规则程度，同时可以作为小天体形心/光心提取方法的选取指标，实现对不同成像特点的算法确定。另外，针对小天体形状不规则度超过设定阈值的情况(即小天体为不规则小天体)，本文提出了一种基于最小外接图形的形心提取方法，实现不规则小天体形心精确提取。该方法受小天体自旋影响小，能够提高小天体形心的提取精度，进而提高自主光学导航的精度。

本文的整体布局如下：首先提出了小天体不规则度的概念，并给出了定义。接着针对小天体探测小天体成像特点，给出了基于小天体不规则度的算法选取准则。针对不规则度较大的小天体，提出了一种基于最小外接图形的小天体形心提取方法，并对该方法进行了详细说明；然后对本文提出的图像处理方法及选取准则进行数值仿真验证和分析；最后给出了文章结论。

1 小天体不规则度定义

不规则图形即没有规则外形的图形，其面积周长等参数的计算没有规律可循。亮度的不规则体现在亮斑每一个像素点灰度值分布的非高斯性。针对距离小天体远近两种不同的成像特点，将小天体形状不规则度和亮度不规则度相结合，提出了一种小天体不规则度(Asteroid irregularity degree，AID)的定义，并作为小天体质心提取的选取指标，小天体不规则度的表达式如下所示：

(1)

1.1 小天体形状不规则度

对于不规则的小天体，因为边缘为不规则曲线，因此无法直接计算边缘点的曲率及投影图形的每一个内角。因此，本文提出了一种基于凸包的小天体形状不规则度的定义方法。根据小天体形状偏离对称性的程度表征形状不规则度。首先对相机拍摄到的小天体原始图像进行阈值分割，接着计算目标小天体的凸包，然后根据小天体的凸包，利用综合判别因素来描述小天体形状的不规则程度。其中小天体形状不规则度的定义如下：

(2)

以三角形为例，首先给出轴对称判别系数Rs的定义。如图1所示，黑色粗箭头直线代表经过三角形ABC重心O点的对称轴MN，三角形ABC为平面投影图形，三角形A1B1C1为ABC的轴对称图形，S为投影三角形ABC的面积，s是投影与其轴对称图形重合部分(阴影区)的面积。通过旋转对称轴MN可以得到阴影区面积的最大值smax，进而可以得到投影图形的轴对称判别系数Rs，表达式如下：

图1 轴对称性判别系数Fig.1 Schematic diagram of ellipse parameters

Rs=1-smax/Sa

(3)

对于尺寸不规则判别系数Rd，其表达式如下：

(4)

式中:di为凸包第i个顶点到等效中心的距离，等效中心可以通过计算凸包顶点的一阶矩得到。d0是由当前图像所求得凸包的等效直径。

对于形状不规则判别系数Ra，其表达式如下：

(5)

式中:θi是凸包多边形的第i个内角，θ0为凸包对应的相同边数的正多边形的内角。

对小天体边缘信息进行提取后，在所建立的初步匹配特征中可能存在误匹配[16]。误匹配边缘曲线的存在极大地影响探测器运动参数的求取，使估计结果出现较大偏差。下面以椭圆为例对拟合残差系数进行说明。这里给出椭圆拟合残差定义：

(6)

当椭圆拟合的残差足够小时(低于阈值下限)，边缘点和椭圆轮廓的近似程度高，采用基于Hough变换的椭圆拟合方法具有很高的可靠性。当椭圆拟合残差大于阈值下限时，边缘点与椭圆的轮廓差距较大，即采用椭圆拟合方法的可靠性较差，此时需要采用适用于不规则边缘的处理算法进行目标天体形心提取。同样可以给出矩形模板和三角形模板的拟合残差。

(7)

因此，针对小天体二维图像，小天体形状不规则度的具体表达形式如下：

(8)

针对三维的小天体，小天体不规则度的具体表达形式如下：

(9)

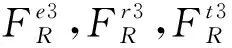
1.2 小天体亮度不规则度

距离小天体较远时小天体在相机中的成像为一个亮点或亮斑，一般其灰度值成高斯分布。本节提出了一种亮度不规则度来描述小天体成像亮度分布的不规则程度。其中小天体亮度不规则度的定义如下：

(10)

偏斜度是对统计数据分布偏斜方向及程度的度量[17]。频数分布分为对称和非对称(偏态)两种。频数分布的示意图如图2所示。在偏态分布中，当偏斜度为正值时，分布不对称，众数位于算术平均数的左侧或右侧。峭度是一个无量纲参数或统计量，用于量化信号相对于高斯分布的分布形状[18]。信号分布的形状分为尖锐，平坦和高斯分布。当信号形状与高斯分布相同时，峭度为零；当信号形状比高斯分布更尖锐时，峭度为正；当信号形状比高斯分布更平坦时，峭度为负。X方向上的偏斜度系数和峭度系数表达式如下。

图2 图像灰度频率分布图Fig.2 Geometric sketch of frequency distribution of image gray values

(11)

因此，小天体亮度不规则度表达式如下：

(12)

式中:Rcy，Rky分别为Y方向上偏斜度系数和峭度系数。根据1.1节和1.2节给出的小天体形状不规则度和小天体亮度不规则度的定义，可以计算出小天体不规则度，具体表达式如下：

μ2((Rcx+Rcy)+(Rkx+Rky))

(13)

当目标小天体图像为一个亮点或亮斑时，μ1=0；反之μ1=1。根据具体任务设计与目标天体参数可以判断目标天体成像特性。本文中假定当小天体所占像素个数小于50时即为亮斑。小天体不规则度可以评定小天体的不规则程度，并可以作为图像处理算法的选取指标。

2 基于小天体不规则度的质心提取算法

小天体探测一般很难提前获取目标小天体的精确形状模型。考虑小天体不规则度的适用性及形心提取方法的可行性，以小天体接近段为例，本节提出了一种基于小天体不规则度的算法选取准则，另外针对小天体不规则度较大的一类小天体，提出了一种最小外接图形的质心提取方法。

2.1 基于小天体不规则度的算法选取

当探测器距离目标小天体相对较近时，小天体在像平面中的投影为一个二维图形，当真实的天体边缘为规则边缘时，采用基于Hough检测提取形心的算法具有较高的精度，而当天体边缘不规则时则具有较大提取误差。当探测器距离目标小天体较远时，小天体在像平面中的成像为一个亮点或亮斑。理想情况下，亮点的灰度值分布应该符合高斯分布，所以采用高斯曲面拟合法有较高的精度，而当亮点灰度值不符合高斯分布时则具有较大提取误差。因此，本文根据相机拍摄的不同时刻的不规则小天体图像，提出了一种基于小天体不规则度的图像处理算法选取准则，选取最合适的小天体形心/光心提取算法。算法选取流程如图3所示。

图3 选取准则Fig.3 Selection criteria based on asteroid irregularity degree

阈值是区分目标规则和不规则的临界值。它是通过基于多场景和多任务图像处理结果的经验获得的。在本文中，根据作者的经验，将火星远，中，近序列图像计算出的不规则度平均值的两倍用作阈值，即4.27。应该指出的是，该值不一定是最优值，阈值选择仍需要进一步的研究。

2.2 不规则小天体形心提取算法

针对小天体不规则度较大的一类小天体，本文提出了一种基于最小外接图形的形心提取方法，该方法先求投影图像的边缘，再根据边缘点求出目标小天体的凸包顶点，然后根据小天体形状不规则度的数值及拟合残差计算凸包顶点的最小外接图形提取形心。该方法确保了计算结果的精确性，提高了不规则小天体形心的提取精度，下面以图4(a)为原始图像，对该提取方法进行详细说明：

1) 图像预处理

图像预处理技术的目的是使相机拍摄的图像更适合于后续处理，一般通过增强感兴趣的区域同时抑制没有实际作用的区域实现。本文采用中值滤波器进行导航图像的预处理。

2) 边缘检测

边缘检测就是利用离散化函数根据二维灰度矩阵梯度向量来寻找图像灰度矩阵的灰度跃变位置，然后在图像中将这些点连接起来就构成了目标的图像边缘。Canny边缘检测是一种常见的边缘提取方法[19]，它利用特定的数字掩码对图像进行滤波运算，具有提取速度快的特点，本文利用Canny算子提取目标的边缘。边缘检测的结果如下图4(b)所示。

3) 计算凸包

凸包是指覆盖平面坐标系内若干点的面积最小的凸多边形[20]，根据步骤2提取的图像中目标小天体边缘轮廓，采用格雷厄姆扫描Graham-Scan算法进行小天体图像边缘的凸包计算，该算法的时间复杂度为O(n)，小天体凸包计算结果如图4(c)所示。

图4 处理结果Fig.4 Processing results

4) 计算最小外接图形提取形心

根据计算得到的小天体凸包，根据拟合残差计算凸包的最小外接图形，最小外接图形的形心即为目标小天体的质心，最终实现导航信息的提取。根据得到的小天体凸包，利用哈奇扬Khachiyan算法计算凸包顶点的最小外接椭圆(MEE)[21]。通过计算面积最小的外接矩形即可得到最小外接矩形(MER)。通过O′Rourke’s算法可以求解凸多边形的最小外接三角形(MET)[22]。该算法通过for循环使某条边依次与多边形的每个边齐平，而不管该边是否是下一个要接触的边。因此，该算法搜索局部极小点的超集，即平面三角形。

3 仿真分析

本节将使用深空导航光学成像半物理仿真系统对本文提出的基于小天体不规则度的质心提取方法进行仿真验证。相机的分辨率为1024×1024。为了解决目标天体建模问题，选用3 ds max进行小天体建模工作。通过对3 ds格式的三维模型进行修改与贴图输出lwo格式，再通过LwConvert格式转换工具将模型格式进行转换，最终通过Open GL调用三维数字模型得到仿真模拟图像。其中小天体模型如图5所示。不失一般性，将模拟小天体质心的真实位置设置在图像的中心，以便更直观地比较处理结果。通过将真实位置与所提算法的提取结果进行比较，可以获得提取误差。另外，对于不规则的小天体图像，对基于小天体不规则度的质心提取方法进行了仿真分析。

图5 三维仿真模型Fig.5 Three-dimensional simulation model

3.1 小天体成像为一个亮点

图6 光点仿真图像Fig.6 Synthetic simulated images of light spot

表1 光心提取结果对比Table 1 Comparison of optical center extraction results

通过仿真可以看出，小天体不规则度能够评价小天体光点亮度分布的不规则程度，并作为算法选取的评价指标。对于不同的成像情况，图像处理精度均小于0.35个像素，证明本文提出的基于小天体不规则度的光心提取方法能够实现不规则小天体光心的精确提取。

3.2 小天体成像为不规则图形

为了验证选择标准的可靠性和所提算法的提取精度，对于图4 (a)中的小天体图像，图7中提供了不同光照条件和小天体自旋状态的仿真图像。根据选择标准选择适当的图像处理算法，结果如图8和表2所示。图8(f)椭圆表示EHT算法的拟合结果，而图8(a～e)椭圆和矩形表示基于MEE和MER算法的处理结果。十字表示小天体的真实位置，星号表示图像处理的质心提取结果。

通过图8和表2可以看出基于小天体不规则度选取后的提取算法有很高的提取精度，形心提取误差小于1个像素，说明了选取准则的有效性，同时证明本文提出的基于外接图形的形心提取算法对于不规则度较大的一类小天体有较高的提取精度。

为了进一步说明选择方法的有效性，图7中的小天体图像使用了四种不同的图像处理算法。图9中显示了图像处理误差曲线。

图7 小天体不同状态模拟图像Fig.7 Synthetic images of asteroid with different states

图8和图9的仿真结果表明，对于不同的光照和旋转状态，所选择的算法具有最高的提取精度，这证明小天体不规则度可以有效地选择不同条件下的图像处理算法。根据表2的处理结果，图像处理精度基本上优于1个像素，并且提取误差的最大值为1.0537。为了进一步验证提取算法在自主光学导航中的可行性，将图像处理误差的最大值作为相机测量误差，并基于图像处理结果对导航性能进行了验证和分析。

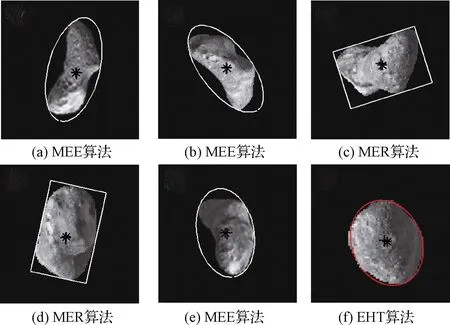
图8 图像处理结果Fig.8 Image processing results

图9 图像处理结果对比Fig.9 Comparison of different image processing algorithm

表2 形心提取结果对比Table 2 Comparison of shape center extraction results

假设摄像机分辨率为1024×1024，视场为1.5°，小天体固定坐标系中探测器的初始状态为[45,000 km，45,000 km，45,000 km，-2 km/s，-1 km/s，-1 km/s]，探测器的初始位置误差为[30，30，30] km，探测器的初始速度误差为[1，1，1] m/s，滤波周期为30 s，仿真时间为1.5×104s。根据小天体接近段的动力学模型和相机测量模型，探测器的估计误差如图10所示。

图10 导航状态估计误差曲线Fig.10 State estimation error curve

从仿真结果分析可知:

1) 针对不规则度较大的小天体，本文提出的基于边缘凸包的最小外接图形进行形心提取的方法具有较高的提取精度，提取误差小于1个像素，同时受光照影响小。

2) 基于Hough变换的形心提取方法对于规则图形边缘具有较高的提取精度，而对于不规则图形边缘精度较差。本文提出的基于小天体不规则度的图像处理方法选取准则，能够选择最优的形心提取方法。通过仿真可以看出，小天体不规则度可以评价小天体的不规则程度，实现算法的选取。对于不同的成像情况，选取后的图像处理精度最高，证明本文提出的基于小天体不规则度可以实现不同算法的有效选取。

3)导航误差曲线表明导航系统具有良好的收敛性。接近段探测器位置估计误差小于1.19 km，速度估计误差小于0.12 m/s。因此，本文提出的质心提取算法的精度满足小天体接近段导航信息提取的精度要求。

4 结 论

本文针对小天体形心、光心提取的问题，提出了小天体不规则度的定义，能够表征小天体的不规则程度。小天体不规则度可以作为图像处理算法的选取指标，针对不同的成像特点采用不同的处理方法，实现对导航形心或光心位置的精确提取。针对小天体不规则度较大的一类小天体，本文提出了一种基于最小外接图形的形心提取方法，该方法受光照和天体自旋影响小，提高了不规则小天体形心的提取精度，最终提高了导航精度。