履带起重机桁架臂破坏性试验及理论分析
孙岱华
(北京市特种设备检测中心技术质量室,北京 100029)
履带起重机在石油化工、核电风电、海洋装备、交通运输等工程建设中应用广泛。随着被吊设备的体积与重量的不断增加,履带起重机的应用占比越来越多[1],安全作业成为这类特种设备的首要问题。履带起重机的桁架臂是重要承载构件之一,为了扩大作业空间,臂架的长度越来越长,一旦出现缺陷,在空间和时间上很难阻止事故的发生,对生命财产构成巨大威胁。因此,合理分析臂架的受力,掌握应力与位移及稳定性的规律,对履带起重机的安全运行至关重要。
履带起重机的危险受力工况不仅在作业状态,很多时候会发生在起臂这种非作业工况。由于臂长,重心远离回转中心,加之结构长细比大,刚性弱,易于出现较大的下挠。与此同时承受变幅拉板对臂架的轴向载荷作用,会进一步加大臂架的下挠量,容易出现臂架变幅平面内的失稳[2]。
为更好地了解和掌握臂架起臂状态下的应力变形及失稳情况,以一个臂节为试验对象,进行起臂状态下的破坏性试验,由此获取结构首先破坏的部位,并依据理论来分析产生破坏的原因,为履带起重机安全运行提供数据支持。
1 臂架的破坏性试验
选取使用频率较高的50 t 级履带起重机臂架为研究对象,受试验条件限制,不能对整体臂架进行破坏性试验,因此按实际臂长,选取重心附近9 m主臂标准节为试验对象,如图1所示。

图1 主臂标准臂节9 mFig.1 9 m section of main boom
根据臂架起臂特点,将臂节置于水平状态,两端支撑[3]。臂架在起臂工况下,会受到臂架自重载荷(垂直于臂架轴线)及变幅拉板引起的轴向载荷作用。由于试验对象9 m臂节两端支撑距离比实际臂长短,长细比也比实际臂长小,因此轴向载荷带来的破坏影响比实际的要小很多。故试验时,仅模拟臂架自重载荷,即垂直臂架轴线的载荷。载荷施加的部位在臂节跨中处。由于载荷比较集中,会引起加载处的结构应力集中,因此对加载处的臂节截面进行了加强,增加了直腹杆(腹杆尺寸与弦杆尺寸相同)。试验时的臂节状态如图2所示。

图2 履带起重机桁架臂Fig.2 The lattice boom of crawler crane
本试验采用多功能电液伺服试验系统对臂架进行逐步加载。当载荷增加至200 kN 时,腹杆Ⅰ发生明显变形。此时载荷急剧下降至110 kN,在该压力保压一定时间后继续加压至腹杆Ⅱ发生变形。载荷下降至135 kN,而后继续加压直至腹杆Ⅲ发生变形,最后卸载。腹杆I、Ⅱ和Ⅲ的位置如图3 所示,载荷施加的历程如图4所示。

图3 失稳的腹杆位置Fig.3 Local buckling failure of auxiliary member

图4 臂架的加载曲线Fig.4 Load curve of boom
从破坏性试验结果来看,腹杆首先出现了失稳,弦杆未见明显变形。结构整体在跨中处竖直方向变形为17.25 mm。
2 试验破坏现象的理论分析
为进一步分析试验破坏的原因,本文首先建立有限元模型,以了解位移与应力分布特点,进而进行稳定性分析,寻找失稳的原因。
2.1 有限元建模
桁架臂是由主弦杆和斜腹杆焊接而成,与梁的结构相近,因此在建立有限元模型时,使用了梁单元模拟弦杆和腹杆,并赋予相应的材料属性和管材规格。根据试验中的支撑方式,在臂节两端的下平面弦杆位置施加静定的位移约束。在实际加载的位置处,对模型施加共200 kN的节点载荷。由此建立的有限元模型如图5所示,节点数为1 006,单元数为1 060。

图5 臂节有限元模型Fig.5 FEM of boom section
2.2 有限元计算结果分析
通过上述的约束条件和载荷条件,对模型进行应力、位移和稳定性计算。臂节的位移云图如图6所示。最大位移在加载处,竖直方向,数值为18.4 mm,这与实测的结果17.25 mm 比较吻合。从某种程度上表明了有限元模型建立的合理性。

图6 臂节位移云图(位移放大倍数5)Fig.6 Displacement cloud diagram of boom section(enlargement factor is 5)
应力云图如图7 所示。最大应力在加载附近的弦杆处,约300 MPa 左右,并沿中间向两侧逐渐减小。弦杆所承受的应力与其材料许用应力500 MPa 相比较小,说明具有较大的安全储备,因此不会出现强度断裂现象。

图7 臂节应力云图Fig.7 Stress cloud diagram of boom section
从图7 中还可以看到,腹杆的应力分布差别较大。加载处的竖直腹杆应力最大,在230 MPa 左右,此腹杆是前述加强腹杆,选用的是弦杆规格和材料,因此安全储备较大。上下平面内腹杆应力很小,因为只施加了竖直方向载荷,未施加侧向水平载荷,故腹杆应力也比较小。前后竖直平面内的斜腹杆应力较大,但比较均匀,在170 MPa 左右。与腹杆的材料许用应力175 MPa 相比,已很接近,若其长细比较大,就容易产生失稳现象。
对比第1主应力(以拉为主的应力)和第3主应力(以压为主的应力)云图,如图8和图9所示。可以看出,竖直平面内的腹杆应力存在拉压交替的现象。

图8 第1主应力云图Fig.8 The first principal stress cloud diagram
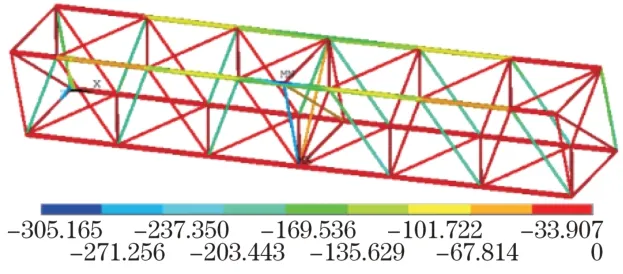
图9 第3主应力云图Fig.9 The third principal stress cloud diagram
此现象与腹杆受力有关,根据力矩平衡原理,垂直于臂架轴线方向的外载荷是通过竖直面内的斜腹杆来传递的。取其中无施加载荷的K 型节点为受力分析对象[4],如图10所示。此节点处无外载荷,不考虑臂节自重,则节点上各杆件的内力之和为0,即两相邻腹杆在竖直方向上的分力之和为0,公式如下:
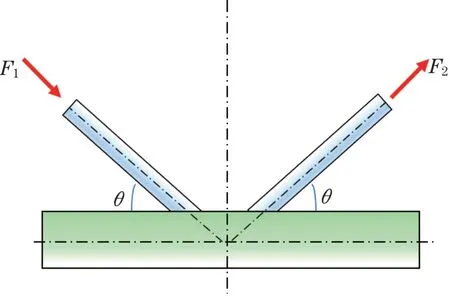
图10 K型节点的受力特点Fig.10 Mechanical characteristic of K-type node

腹杆相对节点对称布置,因此可判别它们的轴向载荷大小相同,方向相反,也就形成了相邻腹杆轴向载荷拉压交替的特点。
进一步分析结构稳定性,相应失稳时的位移云图如图11 所示。可以看到,首先出现的是竖直面内的斜腹杆失稳。根据前面的应力分析,弦杆尺寸规格较大,应力小,相比许用应力,具有较大储备。而腹杆尺寸规格小,材料强度低于弦杆,而且应力接近许用应力,因此腹杆更容易出现失稳。所以失稳云图中位移最大的是竖直平面内的受压斜腹杆,显然首先失稳的也是这些斜腹杆。在这些受压的斜腹杆中,两端的斜腹杆的位移最大,会最先出现失稳,因为其靠近支撑点,会有一定的应力集中。其他斜腹杆应力比较均匀,位移变化也大同小异,表明支撑处的斜腹杆失稳后,随即失稳的就是这些有位移变化的斜腹杆。
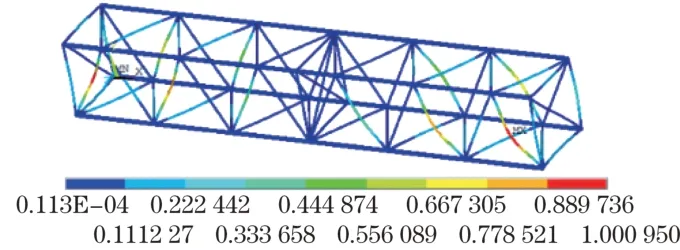
图11 稳定性位移云图Fig.11 Displacement cloud diagram of stability
但理论分析的失稳腹杆与试验结果略有不同。这有可能与各腹杆存在的实际差异有关,如安装误差、焊接缺陷、初始变形、尺寸规格公差等差异[5]。因此,实际失稳时会在相对薄弱的受压斜腹杆上出现。
以壁厚减薄方法为例模拟腹杆间的差异,对试验中受到破坏的腹杆壁厚减薄0.3 mm,结构的失稳云图如图12所示。可以看出,首先失稳的腹杆就是试验中破坏的腹杆I,而且是在腹杆跨中首先失稳,这与试验的变形位置吻合。因为腹杆受轴向压载荷,两端由弦杆约束,相当于两端简支构件,失稳就会出现在中间自由部位。与此同时,试验中相继破坏的腹杆Ⅱ和腹杆Ⅲ在失稳云图中也可以看到位移的变化,表明两者会继腹杆I失稳后而出现失稳。

图12 腹杆壁厚减薄的稳定性位移云图Fig.12 Displacement cloud diagram of stability for auxiliary member after thickness reduced
3 结语
通过理论分析,竖直平面内相邻的斜腹杆在这种加载方式下,所受载荷大小基本相同,方向相反,这是由其构造特点决定的。由于弦杆的尺寸规格、材料都高于腹杆的尺寸规格和材料,因此仅在这种垂直于臂架轴线载荷的作用下,腹杆的应力储备要弱于弦杆,长细比也要高于弦杆,则更容易失稳。所以起臂时,出现腹杆失稳的情况也时有发生,应特别引起重视,一旦出现变形,要及时修复或更换,避免发生事故。本文受试验条件限制,并没有按臂架实际起臂时的臂长和同时作用轴向载荷的方式来进行破坏性试验,但所做的破坏性试验在实际中也有发生的可能,因此要关注臂架起臂时的腹杆表现,这为臂架的使用及后续臂架的检测工作提供了分析基础。

