砂土中螺旋桩纵向振动响应的模型试验研究

张新春，郝洪策，胡 燃，吴 炅，王俊瑜，祝小彦

（1.华北电力大学机械工程系，河北 保定 071003；2.华北电力大学河北省电力机械装备健康维护与失效预防重点实验室，河北 保定 071003；3.广东电网有限责任公司广州供电局输电管理一所，广东 广州 510620）

螺旋桩具有绿色环保、制造工艺简单、施工周期短、易于机械化施工的优势，在各种工程中得到广泛应用，如光伏支架基础、坑壁及边坡支护、海上结构物基础、输电线路铁塔基础等。螺旋桩是一种利用深层土体抗力的桩固结构，一般由一片或多片螺旋叶片焊接在圆形或方形长螺杆或钢杆上，使用特殊的施工机械在螺杆顶部施加一定扭矩将其旋入土体中，其可替代现浇钢筋混凝土基础或预制混凝土独立基础等多种传统基础。

目前，关于螺旋桩的研究已相对较多，张新春等［1］通过模型加载试验，研究了叶片与桩身直径比（D/d）、叶片数量、叶片形式以及加载方式对螺旋桩基础承载特性的影响。Malik 等［2］通过自制模型试验对同等地质下螺旋桩与直桩的端部承载力情况进行了对照分析。郝冬雪等［3］采取有限元分析对可塑黏性土中螺旋桩的上拔承载特性进行研究，分析了螺旋桩几何尺寸对上拔承载力的影响。Elsherbiny 等［4］通过数值模拟与现场测试的对比，验证了数值模型的正确性，得出抗拔理论极限荷载大于数值模拟中极限位移标准（叶片直径的5%）对应的荷载值的结论。Wang 等［5］进行了一维冻胀模型试验，研究了几种螺旋桩和嵌入冻土中无螺旋桩的冻胀特性，分析了温度场、顶推位移对受力承载特性的影响。Cui 等［6］利用ABAQUS软件对同直径螺旋桩和钢桩在黏土中的竖向承载力进行了分析。Dong 等［7］基于泛函理论、突变理论、同时性原理和强度折减法的思想，建立了群桩基础的承载力函数，提出了极限荷载准则和安全储备系数的概念。何泽群等［8］根据竖向上拔承载力与安装过程中抵抗扭矩间的关系，提出了一种安装扭矩理论模型。Li 等［9］研究了桩身在施工过程中承受较大的扭转后，桩身产生包括开裂扭转、极限扭转和扭转变形等破坏。侯典国［10］运用非线性研究方法——p-y曲线法，对横向荷载作用下预制螺旋桩的受力机理进行了分析，进一步丰富了横向荷载作用下预制螺旋桩的理论计算方法。此外，为了进一步提升螺旋桩在实际工程中的应用，张新春等［11］还提出了一种具有良好机械施工性能的叶片可伸缩钢管螺旋桩结构。但目前，对螺旋桩的研究主要集中在静力承载或结构设计方面，对螺旋桩动力响应特性的研究尚浅［12-13］，随着国家对一些重大基建工程中基础的振动频率和纵向位移要求越来越严格，亟须展开对螺旋桩基础纵向振动响应特性的研究。

本文基于自制的桩-土动力相互作用模型试验平台，具体分析了桩体几何参数（长径比L/D、叶片距宽比S/D、叶片外伸比D0/D）以及载荷对螺旋桩模型纵向振动响应特性的影响，给出了桩体几何结构影响螺旋桩纵向振动响应特性的规律。

1 理论研究

由于螺旋桩桩身上有连续或不连续的叶片，其承载力与常规桩型不同，由螺杆的侧阻力、桩端阻力与螺旋处的阻力构成。根据李红文等［14］的计算方法，在计算螺旋桩的承载力时，将螺旋桩看作多点支撑摩擦桩进行考虑，将螺旋桩简化为变截面桩，截面变化处的面积与螺旋桩叶片纵向投影面积相同。螺旋桩的简化模型如图1 所示。图中，L为桩身长度，ρ为桩材料密度，kz为桩端土的弹性系数，ηz为阻尼系数。

图1 螺旋桩简化模型Fig.1 Simplified model of spiral pile

根据桩身的截面变化，将桩分为互相连接的n段，任一截面变化处对应一条虚拟土层分界线，定义坐标为Li。土层对应的桩身截面面积为Si，长度为Li-Li-1，任一桩截面对应的土层弹性系数为Ki，阻尼系数为ηi。模型假设条件为：①桩体为确定长度的变截面均质杆体，材质为黏弹性杆材料，且为Voigt 形式，杨氏模量为E，黏滞系数为ηp；② 桩端土体简化为线性阻尼器ηz和理想弹簧Kz并联的形式；③桩侧土体简化为线性阻尼器ηi和理想弹簧Ki并联的形式；④桩径尺寸远小于桩长；⑤桩受到的纵向载荷均匀地作用在桩的端面上；⑥桩在振动时各部分仅发生线性变化。对第Li-1-Li段的桩身微元建立振动微分方程，可得平衡方程为

式中：E和ρ分别为弹性杆材料的杨氏模量和密度；ηa为黏滞系数；ui为第i层土对应桩段的纵向位移，i=1，2，…，n。

对式（1）进行无量纲化处理，得到初始条件为

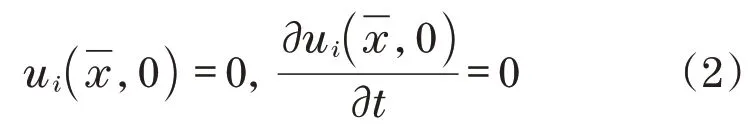
经过Laplace变换，可得

式中：Y1、Y2分别为s的运算矩阵；γρ为桩身阻尼因子；L为桩身长度。

令式（3）中s=jω为圆频率，将Laplace 变换转化为傅里叶变换，则得桩顶位移频响函数为

速度频响函数为

式中：＊符号表示卷积计算。

根据式（6），验证了叶片数量及叶片在桩身的不同位置对螺旋桩纵向振动性能的影响。分别对不同叶片数量螺旋桩施加相同的冲击速度，桩顶速度响应因子随时间变化曲线如图2 所示。图中可见，在一定载荷范围内以及稳定土基条件下，螺旋桩承受纵向承载能力未随叶片数量的增多而明显增强。图3 为相同冲击载荷下不同叶片位置模型桩顶速度响应曲线。在桩体承受相同载荷时，桩顶速度未随叶片位置改变而发生明显变化。

图2 不同叶片数量桩模型桩顶速度响应曲线Fig.2 Pile top velocity response curve of pile model with different number of blades

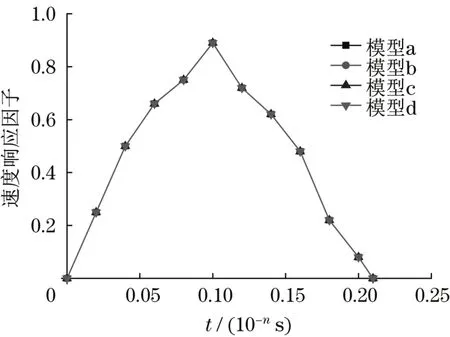
图3 不同叶片位置桩模型桩顶速度响应曲线Fig.3 Pile top velocity response curve of pile model with different blade positions

通过以上分析可知，螺旋桩模型在承受载荷过程中未随叶片数量的增多而明显增强，且在承受相同载荷时，桩顶速度未随叶片位置变化而发生明显的改变，验证了叶片位置未对螺旋桩纵向振动特性产生影响。故在实验中可排除不同位置或不同叶片数量引起的纵向振动特性的差异。

2 螺旋桩纵向振动响应的模型试验研究

2.1 试验原理

本次试验依托外力冲击螺旋桩顶部产生激振信号，即使用力锤对桩模型顶部施加冲击载荷，并依靠激振系统传递激振信号及测试分析系统测量螺旋桩模型的共振频率。测试分析系统通过固定于桩顶的加速度传感器测得桩顶振动加速度信号，并对其进行傅里叶变换，得到桩模型的共振频率。试验分析对比不同几何参数以及桩顶承受不同载荷条件下的桩模型共振频率变化情况，进而研究螺旋桩动力响应特性变化规律。试验过程中假设条件为：箱体不随试件振动，忽略土塞效应的影响。

2.2 试验用土及桩模型

试验用土为砂土，通过采样测量得到其物理性质：土体密度ρ=1 950 kg·m-3，土体黏聚力c=0，内摩擦角φ=32°。试验中砂土分层填入捣实，桩模型埋入后静置24 h。

本次试验共制作三组钢管螺旋桩，其中两组分别控制叶片宽度、叶片间距参数不同，其他参数保持一致；另一组为控制长径比参数不同的直桩模型，模型桩及试件结构如图4和图5所示。

图4 桩试验模型Fig.4 Test model of pile

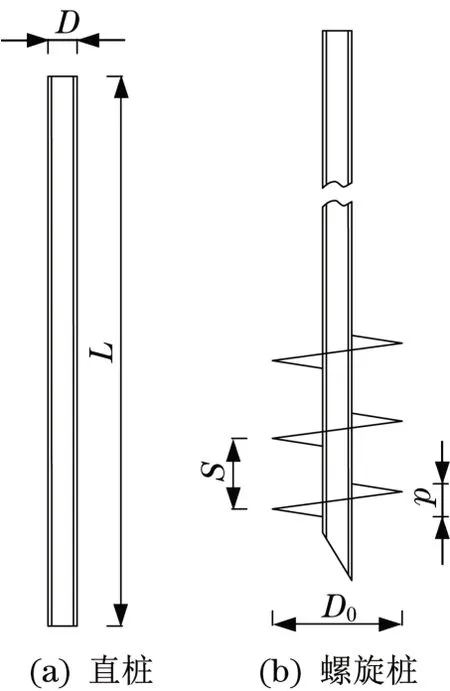
图5 试件结构Fig.5 Specimen structure

桩模型选用Q345 不锈钢材料，弹性模量为206 GPa，泊松比为0.28，桩模型桩身光滑，忽略与土体的摩擦。螺旋桩模型均采用分层式三叶片模式布局，即叶片间螺距相同，开口方向一致，旋向相同。叶片等间距焊接于桩身预定位置，叶片倾角为90°，桩模型底端为楔型角，角度为45°，详细参数如表1所示。桩顶部焊接受力钢板，以保证其受顶部冲击时受力均匀。另外，在桩模型顶部水平焊接两个钢片，以达到粘贴加速度传感器并传递信号的作用。

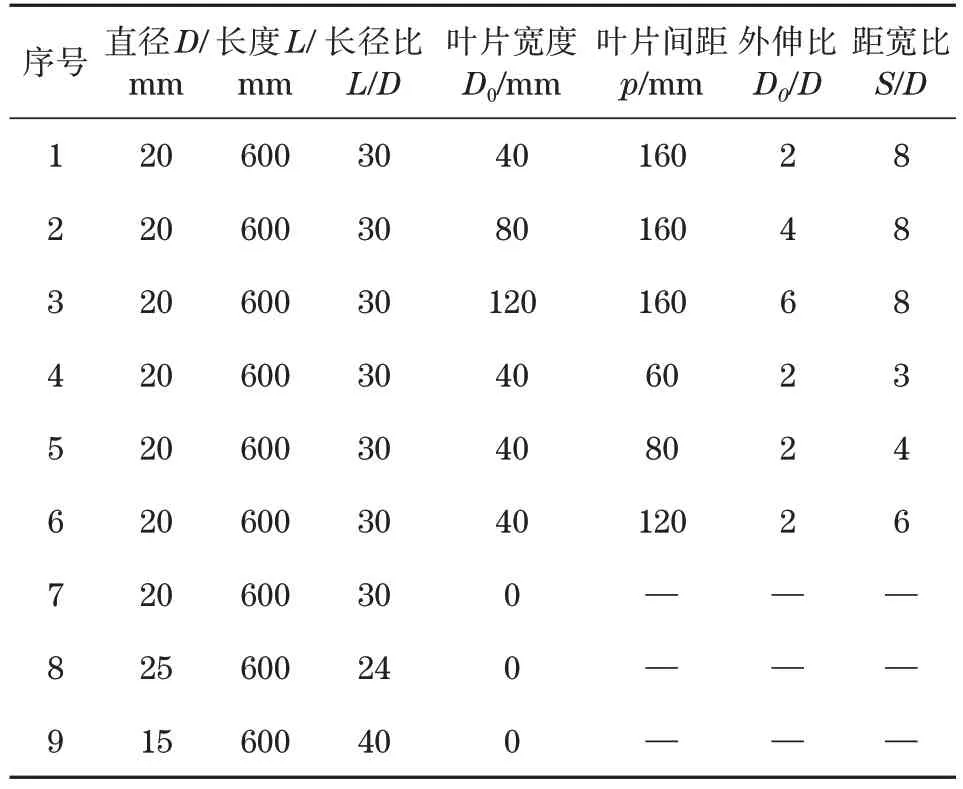
表1 桩模型几何参数Tab.1 Geometric parameters of pile model

2.3 试验设备

自制试验平台由3 部分组成，包括激振系统、测试分析系统、承载系统，如图6 所示。承载系统为自制砂箱，材料为Q345 钢，尺寸为0.6 m×0.6 m×1.0 m（长×宽×高），除砂箱顶面不密封外，四壁及底面均密封，四壁由矩形钢管加固。因砂箱体积有限，砂箱边界对箱内砂土和模型桩起约束作用，即易产生边界效应，为消除边界反射波的影响，特于砂箱内壁粘贴2 cm厚塑料泡沫板。

图6 模型试验平台示意图Fig.6 Schematic diagram of model test platform

测试分析系统包括压电式压力传感器、加速度传感器、DH5923N 动态信号测试系统。压电式压力传感器安装于力锤端部，用来测量敲击力；加速度传感器用蜂蜡粘贴于桩顶焊接的钢片上，用于测量振动时加速度变化情况；压力传感器及加速度传感器的输出信号由DH5923N 动态信号测试系统采集分析。

2.4 试验结果与讨论

通过对表1 中模型2 和7 的振动敲击试验，采集桩模型在承受不同纵向载荷时桩顶加速度信号，并通过傅里叶变换将信号进行时频域变换，如图7所示。此试验桩模型使用表1 中模型2 和7，图8 给出了不同冲击载荷条件下共振频率。在承受不同冲击载荷下，同一桩模型共振频率发生不同程度的衰减。通过对比直桩模型与螺旋桩模型的试验结果，对于长径比相同的桩模型，在模型承受相同载荷时，螺旋桩模型的共振频率远高于直桩。

图7 信号处理Fig.7 Signal processing

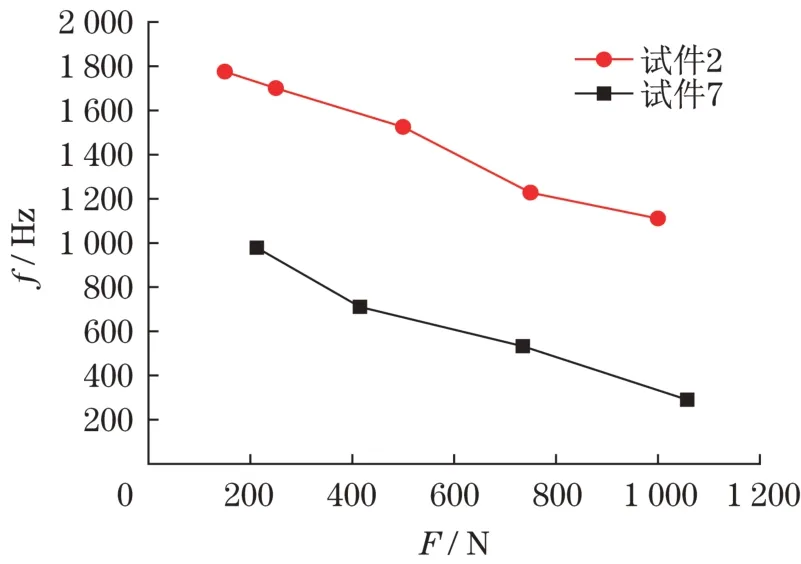
图8 载荷对桩模型共振频率的影响Fig.8 Influence of load on resonance frequency of pile model

在保持激振载荷不变的条件下，图9 给出了长径比（L/D）对直桩模型共振频率的影响。图中可见，直桩模型共振频率与长径比呈负相关。图10给出了叶片外伸比对螺旋桩模型振动响应特性的影响。在保证桩模型的叶片外伸比不同、其他结构参数及冲击载荷相同时，螺旋桩模型共振频率随叶片外伸比增大呈增加趋势。另外，桩顶受到相同冲击载荷时，桩顶纵向最大加速度随叶片外伸比的增大呈减小趋势。

图9 长径比（L/D）对直桩模型共振频率的影响Fig.9 Infiuence of length to diameter ratio（L/D）on resonant frequency of straight pile model

图10 给出了叶片外伸比对螺旋桩模型振动响应特性的影响。在保证桩模型的叶片外伸比不同、其他结构参数及冲击载荷相同时，螺旋桩模型共振频率随叶片外伸比增大呈增加趋势。另外，桩顶受到相同冲击载荷时，桩顶纵向最大加速度随叶片外伸比的增大呈减小趋势。

图10 叶片外伸比对桩模型振动响应特性的影响Fig.10 Influence of blade extension ratio on vibration response characteristics of pile model

据图11 可知，在相同冲击载荷下，螺旋桩模型的共振频率未随距宽比改变而呈现明显的变化。作为对比，图11 还给出了相同冲击载荷下叶片距宽比对桩顶最大加速度的影响。螺旋桩模型在受到冲击载荷时桩顶最大加速度也未随距宽比的变化发生明显改变。结果表明，螺旋桩模型纵向振动响应不敏感于叶片距宽比。

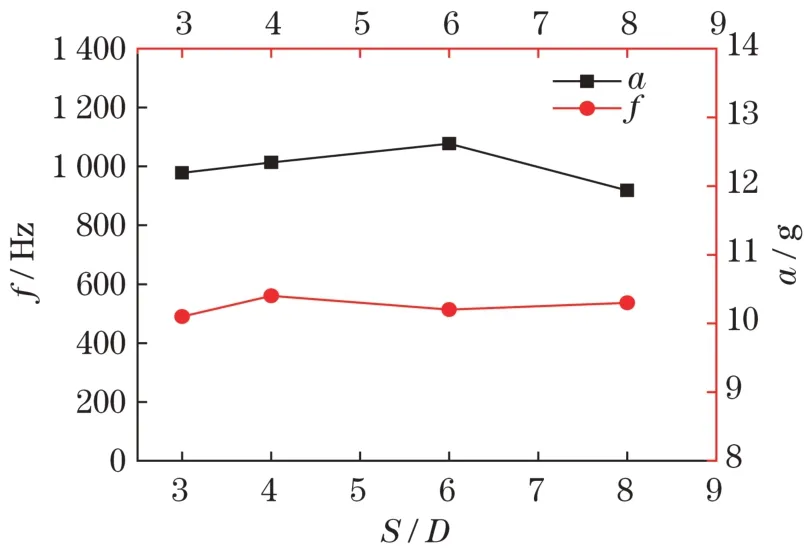
图11 叶片距宽比对桩模型振动响应特性的影响Fig.11 Influence of the blade spacing-width ratios on vibration response characteristics of pile model

3 结论

通过自制的桩-土动力相互作用模型试验平台，研究了桩体几何结构对桩模型纵向振动响应特性的影响，得到如下结论：①随着冲击载荷的增大，螺旋桩与直桩模型的共振频率均呈逐渐减小的趋势。②长径比是影响桩模型共振频率的重要因素，在保证其他参数不变的前提下，桩模型的纵向共振频率随长径比的增加而减小，但螺旋桩模型共振频率与叶片外伸比呈正相关变化趋势。③叶片距宽比对螺旋桩纵向振动响应特性的影响不明显，在保证其他参数及载荷不变时，螺旋桩模型共振频率不敏感于叶片距宽比。