混凝土泵车整车有限元模态分析与试验
智晋宁,张浩杰,王志强,张喜清,任亚峰,赵 伟
(1.太原科技大学机械工程学院,山西 太原 030024;2.徐州徐工施维英机械有限公司泵送机械研究所,江苏 徐州 221004)
混凝土泵车以其浇筑速度快和效率高等优点,逐渐成为生产建设中不可缺少的重要工具。混凝土泵车在泵送过程中,由于输送管内冲击载荷与中心泵换向冲击会造成臂架振动,当泵送频率接近整车固有频率时还会引起共振现象[1]。因此,模态分析作为混凝土泵车减振分析的基础工作,具有重要的意义。
刘荣升等[2]采用解析法对混凝土泵车臂架系统进行了模态求解,得到各阶固有频率和振型,然后通过试验对固有频率进行了验证;朱详华等[3]建立了混凝土泵车臂架有限元模型,通过模态求解得出了固有频率的分布范围,并对油缸和连杆机构进行了参数优化;吕彭民等[4]通过对泵车有限元模型进行灵敏度分析和动态优化,提高了固有频率而避免了共振;Wang 等[5]模拟了固有频率与管径和流速的关系,分析了流固耦合作用对臂架结构固有频率的影响;黄毅等[6]在ADAMS 振动模块中对臂架进行了模态分析,并与试验结果进行了对比,验证了所搭建刚柔耦合模型的准确性。
针对大多数混凝土泵车的模态分析只以臂架为研究对象,而忽略了下车系统对整车结构模态的影响,本文以某型号混凝土泵车整车为研究对象,基于HyperWorks 软件进行整车有限元模型搭建,通过赋予输送管混凝土等效密度模拟整车满管状态,采用Block Lanczos 方法进行整车模态求解。同时还求解了上车模型(含转台)及空管模型的模态结果,对比分析了混凝土泵车满管与空管、整车和上车的固有频率。最后通过实车模态试验,验证本文搭建有限元模型的准确性。
1 模态分析理论
模态分析是研究物体结构振动特性的常用手段,物体的振动特性包括其固有频率和振型等,是结构承受动态载荷的重要参数[7]。通过模态分析可以实现避免共振和控制噪声的作用,为结构优化设计提供可靠依据。有阻尼系统振动微分方程为

在有限元模型中多采用无阻尼自由振动系统[8],振动微分方程为

假设方程存在特解为

式中:φ为响应幅值列阵。联立式(3)和式(2)整理后可得
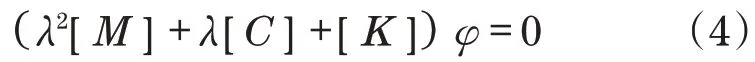
式(4)的特征方程为

解得方程特征值为

式中:-δi为系统衰减系数;ωi为有阻尼系统固有频率;ω0为无阻尼系统固有频率。
2 有限元建模与模态分析
2.1 整车有限元建模
混凝土泵车整车结构简图如图1 所示。首先在SolidWorks 中对各部件的几何结构进行简化,并按照臂架水平姿态进行整车装配。

图1 混凝土泵车整车结构简图Fig.1 Concrete pump truck structure diagram
在HyperWorks 软件中建立整车有限元模型,用板壳单元模拟臂架、转台、副车架等各总成,用全约束WELD 单元模拟组件间的焊接关系,用CBUSH 弹簧单元模拟油缸液压油,用CONM 质量单元代替副车架、底盘、中心泵等附件,用组合的RBE2单元模拟销轴并放开转动自由度。为了提高计算精度并减小计算周期,采用大小为20 mm 的CQUAD4 壳单元、CTETRA 四面体单元和CHEXA六面体单元相互组合进行网格划分;整车水平姿态有限元模型如图2 所示,整车有限元模型的节点数为143万,单元数为217万。

图2 水平姿态整车有限元模型Fig.2 Finite element model of the whole vehicle with horizontal attitude
整车有限元模型采用各材料参数如表1示。
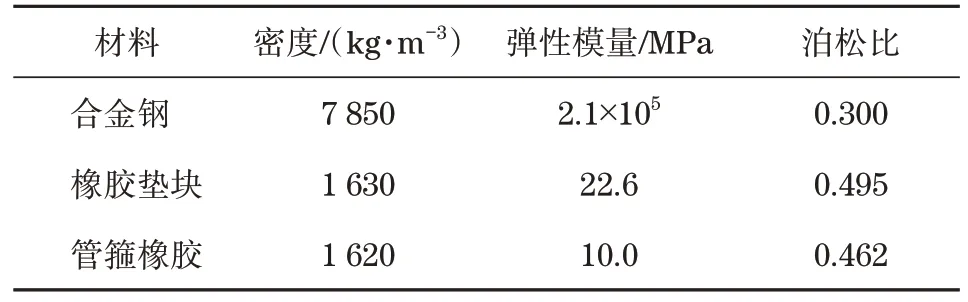
表1 整车有限元模型各材料参数Tab.1 Material parameters of the whole vehicle finite model
通过计算得到整车各输送管混凝土质量的等效模型,在整车有限元模型上通过赋予输送管混凝土等效密度来模拟满管状态。各段输送管混凝土等效密度计算公式为

式中:ms为输送管质量,kg;mc为混凝土质量,kg;Vs为输送管体积,m3。
有限元模型油缸刚度计算公式为[9]
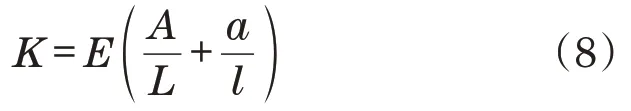
式中:E为液压油体积弹性模量(Pa);A为油缸无杆端面积(m2);L为油缸无杆端长度(m);a为油缸有杆端面积(m2);l为油缸有杆端长度(m)。
2.2 整车模态分析
模态分析作为瞬态动力学分析、谐响应分析和谱分析的起点,是结构振动分析、可靠性设计及优化以及故障诊断的重要方法[10]。对泵车4 条支腿进行约束,检查网格质量降低QI 指数,赋予各单元材料和属性参数,对整车输送管添加等效密度并赋予各油缸刚度。创建模态分析载荷步,采用精度较高且收敛较快的Block Lanczos方法进行整车模态分析[11-12],整车前 6 阶满管模态计算结果如表 2 所示,其中前4阶模态振型如图3~图6所示。

图6 整车第4阶模态振型Fig.6 The fourth vibration mode of the whole vehicle

表2 整车前6阶模态Tab.2 The first six modes of the whole vehicle

图3 整车第1阶模态振型Fig.3 The first vibration mode of the whole vehicle

图4 整车第2阶模态振型Fig.4 The second vibration mode of the whole vehicle

图5 整车第3阶模态振型Fig.5 The third vibration mode of the whole vehicle
低阶固有频率对分析动态特性更有参考价值[13],因此前2 阶模态特性对系统影响较大。从振型看,此款泵车1 阶、2 阶振型分别为臂架在水平面和竖直面内的弯曲振动,且频率接近于低泵送频率区间9~12 次/min,即0.15~0.2 Hz,存在共振的可能。因此,此款泵车应尽量避免低泵送频率工况。
3 模态影响因素分析
3.1 臂架与整车模态对比
常规的混凝土泵车模态分析建模时一般只选取臂架系统,忽略了下车质量和刚度的影响。考虑下车结构对整车模态的影响,单独对臂架系统进行模态分析,可得上车计算模态与整车计算模态数据对比如表3所示。

表3 上车模态与整车模态对比Tab.3 Comparison of upper vehicle mode and whole vehicle mode
现有研究多数以混凝土泵车臂架为研究对象进行模态分析和结构振动分析,导致求解结果与泵车真实模态和振动特性存在差异。通过模态分析可知,上车系统与整车系统固有频率差别较大,变化率最大为10.5%,证实了泵车上车与下车之间存在着互相影响的耦合关系[14-15],各子系统之间互相作用共同影响整车系统的模态以及动力学效应,是一个不可分割的整体[16]。
3.2 空管与满管模态对比
考虑混凝土质量对振动模态的影响,因此有必要对整车空管模态进行求解。在整车满管有限元模型上去除混凝土等效质量,改为空管模型,其他参数设置保持不变,进行模态求解。整车空管模态与整车满管模态数据对比如表4 所示。对比分析可知,满管相对于空管前几阶固有频率减小10%以上,其中前2阶模态变化率最大,接近于20%。因此混凝土质量对整车结构模态存在较大影响,且对低阶模态影响最为突出。

表4 空管模态与满管模态对比Tab.4 Comparison of empty pipe vehicle mode and full pipe vehicle mode
通过模态对比结果可以看出,相同阶次空管模型的模态频率最大,满管模型的模态频率最小;上车相对于整车而言,第1 阶固有频率增加了8.1%,空管相对于满管而言,第1 阶固有频率增加了18.1%。因此可知,混凝土质量和下车结构都会对整车结构模态造成不同程度的影响。
4 实车模态试验
4.1 模态试验方案
调整臂架姿态近似为模态分析的水平姿态,在臂架末端施加强制位移后突然释放,对臂架系统进行激振。利用PSV 扫描式激光测振仪依次扫描每节臂架的下盖板和侧板,采集振动速度信号,同时在被测臂架面板处安装加速度传感器,采集振动加速度信号,数据经处理后获得整车固有频率。
整车模拟满管试验时,首先按照计算结果在臂架上安装配重。在臂架末端垂直方向安装加速度传感器,利用激光测振仪扫描头内置的高清CCD传来的目标图像,在计算机测试界面上定义2D Alignment 点,通过AD 设置对测量参数进行设置,然后定义扫描点。测Y向数据时加载方式为末端Y向强制位移50 cm 后突然释放,测Z向数据时加载方式为末端Z向强制位移50 cm 后突然释放,确保释放位移时激光测振仪与加速度计同时开始采集信号。测量结束后导出数据进行后处理分析,模态频率多次测量取平均值。试验现场图如图7所示。

图7 整车满管模态试验现场图Fig.7 Full pipe of whole vehicle modal test site diagram
4.2 试验结果分析
如图8(a)和图8(b)所示,分别为空管试验和满管试验所得臂架末端速度曲线图,对Y向试验数据进行分析,通过傅里叶变换和细化处理得到臂架末端速度频谱曲线如图9 所示,采用单自由度法获取模态数据,得到每阶固有频率试验值。

图8 臂架末端速度曲线Fig.8 The velocity curve of the boom end

图9 臂架末端速度频谱曲线Fig.9 Velocity spectrum curve of the boom end
通常采用误差率来判定计算模态与试验模态之间的相关性大小。由于不同的分析对象允许的误差率大小不同,通常情况下认为计算模态与试验模态的误差率在10%以内,两者相关性较好,计算模态与试验模态对比结果如表5 所示。通过对比前4 阶固有频率可知,模态频率的计算结果与试验结果平均误差率在5%以内,证实了本文所搭建的模态求解模型具有较好的准确性。

表5 固有频率对比表Tab.5 Natural frequency contrast table
5 结论
本文针对某型号混凝土泵车整车模型、上车模型和空管模型进行了模态分析,并通过试验加以验证,可得以下结论:①当不考虑下车的影响时,臂架固有频率相对于整车固有频率最大增加了10.5%,因此,只对上车系统进行模态分析会与泵车真实固有频率产生较大差别,证实了混凝土泵车上车与下车之间存在着耦合作用关系,共同影响着整车的结构模态及振动机理。②混凝土泵车空管状态相对于满管状态固有频率增加了10%~20%,混凝土对整车振动模态具有较大影响,且对低阶模态影响较为突出。③从整车固有频率可以看出,当泵送频率接近于0.2 Hz时,激励频率分别与系统第1阶和第2阶固有频率接近,有产生共振的可能。因此为避免共振现象发生,泵车应尽量避免12 次/min 泵送频率工况。④通过计算模态与试验模态对比可知,平均误差率小于5%,验证了本文所搭建的满管模型具有较好的准确性和真实性,能够较为真实地反映此款泵车机械结构的振动特性,为整车固有频率的优化设计和瞬态动力学求解奠定了基础。

