基于MIDAS的贝雷梁加强处理建模技术研究
胡帮义,徐学勇,胡丽珍,刘颖
(1.湖州职业技术学院,浙江 湖州 313000;2.湖州市绿色建筑技术重点实验室,浙江 湖州 313000)
0 引言
贝雷梁是一种装配式制式钢梁结构,具有安装拆卸方便[1]、标准化程度高、装配化施工、成本较低的优点,在路桥施工现场得到了广泛的应用。常用来搭设临时钢便桥[2]、搭设桥梁现浇支架[3]、拼装挂篮[4]及架桥机等,这些结构的安全直接影响桥梁施工的安全。因此,对贝雷梁进行受力分析及安全计算具有重要的意义。
目前主流的计算方法有两种,一种是简化成平面结构手算或局部电算[5],另一种是采用有限元软件建立三维空间有限元计算模型整体计算[6-7],从而查看结构的应力或内力[8],与容许值进行比较。第一种方法具有简单快捷的特点,但荷载的计算往往难以精确计算。第二种方法可以比较精确模拟结构的受力情况,但是建模较复杂。但不管哪种方法,都会出现结构局部受力较大以及应力超限的情况。在这种情况下,需要对贝雷梁支架进行加强处理[9]。那么如何对加强的杆件进行建模分析以便合理模拟实际受力情况,则是一个值得研究的课题。
本文采用Midas Civil有限元软件对对某贝雷梁进行了加强处理有限元建模分析,对加强弦杆提出了两种建模方法,对加强竖杆提出了“以曲代直”的建模方法,可为类似工程的建模分析提供方法参考。
1 单排贝雷梁受力超限假定
1.1 单排贝雷梁受力工况
大河兜桥边跨现浇段施工支架采用贝雷梁作为主梁,贝雷梁的验算是保证支架安全的重要因素。初步分析该支架单排贝雷梁受到均布荷载60kN/m,跨度为12m,由4 片贝雷梁拼装而成。受力形式如图1所示。

图1 贝雷梁受力简图
1.2 单排贝雷梁受力计算
1.2.1 有限元建模计算
采用Midas Civil 软件建模计算,建立了贝雷梁的有限元计算模型。贝雷梁杆件均采用梁单元模拟,共建立了节点62 个、梁单元104 个。建立的有限元计算模型如图2所示。
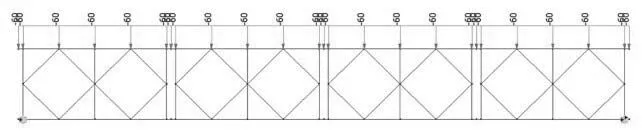
图2 贝雷梁MIDAS有限元计算模型
1.2.2 有限元计算结果
通过有限元计算,可以得到贝雷梁的正应力如图3所示。

图3 贝雷梁正应图(正应力,单位:MPa)
由图3 可知:贝雷梁正应力为515.7MPa>[σ]=305MPa,故贝雷梁不满足受力要求,需要进行加强处理。
值得说明的是,贝雷梁材质为16Mn 钢,对应现在钢号为Q345 钢,查《钢结构设计标准》(GB 50013-2017)[10]可知,容许正应力为305MPa,容许剪应力为175MPa。
为了明确加强处理的方法,需明确上下弦杆和腹杆具体超限的位置和大小。上下弦杆正应力如图4 所示,腹杆正应力如图5所示。

图4 贝雷梁上下弦杆正应图(正应力,单位:MPa)

图5 贝雷梁腹杆正应图(正应力,单位:MPa)
可见贝雷梁弦杆和腹杆应力均有超标,如何对上下弦杆和腹杆进行加强处理并进行有限元合理模拟是一个值得研究的课题。
2 上下弦杆加强处理
2.1 加强处理方法
结合工程实践经验,工地现场多采用在弦杆上增设加强弦杆来进行加强处理,加强弦杆材质、截面和弦杆一致,采用螺栓连接固定在弦杆上。下面采用两种方法来模拟加强弦杆的建模,以便进行对比分析。
2.2 单截面模拟加强弦杆法
加强弦杆固定在原来的弦杆上,两者协同受力,故可以把两者看成一根杆件,新杆件的截面为原来弦杆截面的叠加,新截面如图6所示。

图6 弦杆新组合截面
2.2.1 有限元计算模型
在Midas Civil软件中利用截面特性计算器,自定义该组合截面进行建模计算,同理可以建立贝雷梁的有限元计算模型如图7所示。

图7 增加加强弦杆后有限元计算模型
2.2.2 有限元计算结果
有限元计算可以得到贝雷梁弦杆的正应力如图8所示。

图8 增加加强弦杆后弦杆正应力图
由图8 可知,弦杆最大正应力为185.5MPa<[σ]=305MPa,故增设加强弦杆后贝雷梁能够满足受力要求。
2.3 双截面模拟加强弦杆法
加强弦杆固定在原来的弦杆上,两者协同受力,可以单独用梁单元来模拟原来的弦杆和增加的加强弦杆,上下梁单元之间采用刚性连接模拟螺栓连接,该建模方法如图9所示。
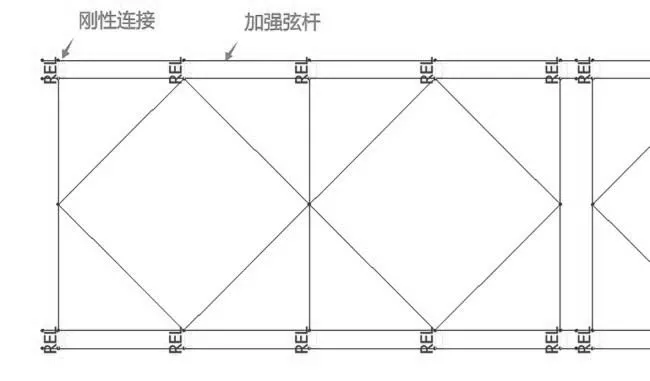
图9 双截面模拟加强弦杆方法
2.3.1 有限元计算模型
同理可以建立贝雷梁的有限元计算模型如图10所示。
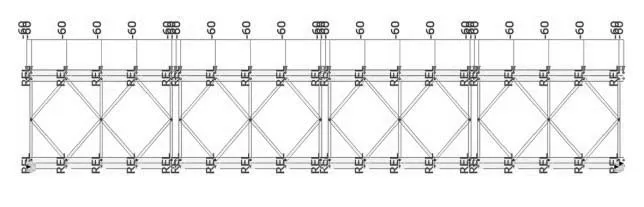
图10 增加加强弦杆后有限元计算模型
2.3.2 有限元计算结果
有限元计算可以得到贝雷梁弦杆的正应力如图11所示。

图11 增加加强弦杆后弦杆正应力图
由图11 可知,弦杆最大正应力为186.1MPa<[σ]=305MPa,故增设加强弦杆后贝雷梁能够满足受力要求。
根据单截面模拟加强弦杆法得到的弦杆最大正应力185.5MPa,两种方法所得结果误差仅0.3%,说明两种方法均较好地模拟了贝雷梁加强弦杆的受力情况。
3 支点处竖杆加强处理
3.1 加强处理方法
结合工程实践经验,工地现场多采用在支点位置增设1~2 根10#槽钢加强处理的方式。本贝雷梁采用增加2 根10#槽钢的办法加强处理。本文提出“以曲代直”的办法模拟,具体实施方法如图12 所示。AB 为原结构竖杆,A1KB1和A2KB2为两根加强竖杆,截面为10#槽钢,当AA1、AA2、BB1、BB2的长度趋于0时,他们将趋于AB杆实现协同受力。本文取AA1=AA2=BB1=BB2=10cm 进行建模计算。

图12 加强竖杆以曲代直法建模
3.2 有限元计算模型
同理可以建立增加了加强竖杆的贝雷梁有限元计算模型如图13所示。

图13 增加加强竖杆后有限元计算模型
3.3 有限元计算结果
有限元计算可以得到增加了加强竖杆后的贝雷梁腹杆正应力如图14所示。

图14 增加加强竖杆后腹杆正应力图
由图14 可知,腹杆最大正应力为256.8MPa<[σ]=305MPa,故增设加强竖杆后贝雷梁能够满足受力要求。加强竖杆的正应力如图15所示。

图15 加强竖杆的正应力图
由图15 可知,加强竖杆最大正应力为148.6MPa<[σ]=215MPa,故增设的2道加强竖杆采用10#槽钢能够满足受力要求。
4 结语
通过结合贝雷梁加强处理工程实践经验和Midas 有限元计算结果,可以得出以下结论:
①针对贝雷梁弦杆承载能力不足增设加强弦杆的情况,提出了“单截面模拟加强弦杆法”和“双截面模拟加强弦杆法”两种Midas 建模方法,两种方法有限元建模计算结果非常一致,误差仅0.3%,均较好地模拟了贝雷梁加强处理的协同受力情况;
②针对贝雷梁竖杆应力超标的情况,增设了10#槽钢作为加强弦杆,提出了“以曲代直”的建模方法,较好地模拟了加强竖杆的受力情况;
③本文所述贝雷梁加强处理有限元建模方法可为类似工程的有限元建模提供方法参考。

