激光捷联惯导动态精度提升技术综述

李成麟，雷旭亮，陆煜明，陶彧敏

（1.北京航天时代激光导航技术有限责任公司，北京 100094；2.北京航天控制仪器研究所，北京 100039）

0 引言

惯导作为一种全时空、全方位敏感载体姿态、速度、位置的精密仪器，其工作环境往往十分恶劣。以各类战略战术导弹为例，其振动可来自于冲压喷气发动机或固体火箭发动机不稳定燃烧振动、空气附面层涡流引发的导弹蒙皮结构振动、过载与超高速飞行时翼面与操纵面的流动分离涡流引发的振动，其频带跨度为0Hz～2000Hz，振动强度大、随机性高。过载段加速度则常在10g量级，最高可至30g量级。

激光捷联惯导的动态误差源主要包括：

1）惯性器件动态误差：在高动态环境下，惯性器件内部结构的复杂变化将导致其产生动态误差，如激光陀螺谐振腔扭转、加速度计摆片偏移工作位置等造成的零偏误差、标度因数误差、非线性误差等。激光陀螺为全固态光学陀螺，本身具有较好的动态性能，其动态误差主要来源于大过载与大角加速度环境的抖动轴弯曲所导致的敏感轴偏移，0.4″的偏角可显著产生 0.232（°）/h 的等效零偏［1］；大过载下对加速度计二阶项的10-7（g/g2）的标定误差在10g过载下可产生10-5g的等效零偏，两者对于高精度惯导的影响显著。

2）惯 性 测 量 单 元 （Inertial Measurement Unit，IMU）结构形变误差：陀螺仪与加速度计通过螺钉固联在本体支架上，其在高动态环境下发生位移，且本体支架本身也会受力变形，从而造成安装误差以及加速度计杆臂的变形，工程上通过结构模态设计、精密加工装配和减振来控制该项误差，机械结构变化带来的误差相比惯性器件本身的误差较小。

3）导航算法误差：高动态环境下常伴随着剧烈的圆锥运动与划桨运动，导致矢量积分产生较大的不可交换性误差，文献［2］通过对动态环境下的多源动态误差仿真分析得出，圆锥运动在160s导航时间内带来的位置误差在103m量级。经典圆锥补偿算法与划桨误差补偿算法可补偿大部分不可交换性误差，理论上四子样算法即可达到10-8（°）/h量级的算法漂移精度，但由于算法推导存在近似误差，在大锥角圆锥运动与大角度机动的高动态环境下这种误差被放大。

4）减振器误差：早期的捷联惯导采用硬捷联，惯导直接固联在载体上，导致其受到强烈的低频运动冲击和振动影响；而软捷联通过减振器将测量单元与载体隔离，使捷联惯导的实际动态环境中工作应用成为可能。然而，目前的惯导设计对大过载下与大温差下的减振器性能变化缺乏考量，大过载下的2.5mm的减振器形变产生的非线性刚度可导致传递特性发生10Hz的固有频率改变以及0.5dB的幅值改变［3］，而温度对此的影响更为显著，其导致的模态设计和信号矫正滤波器失效显著降低了惯导在动态环境中的可靠性。

据此，本文将以机抖激光陀螺与石英挠性加速度计组合的激光捷联惯导为对象，首先在惯性器件方面，重点探讨了激光陀螺的抖动轴弯曲的影响与解决措施，以及石英挠性加速度计摆片动态性能及其带来的非线性误差的标定；其次在惯导减振器方面，探讨了现有的减振系统设计以及工程上忽略的大位移与温差对减振器非线性动态特性的影响；再次，梳理了动态环境下导航算法的发展情况；最后，对激光捷连惯导动态精度提升技术未来的研究方向进行了展望。

1 惯性器件动态精度研究

1.1 激光陀螺

机抖激光陀螺作为基于Sagnac原理的全固态光学陀螺，由于不存在活动的机械转子，相比传统机械陀螺在动态性能上有质的提升，其结构如图1所示。

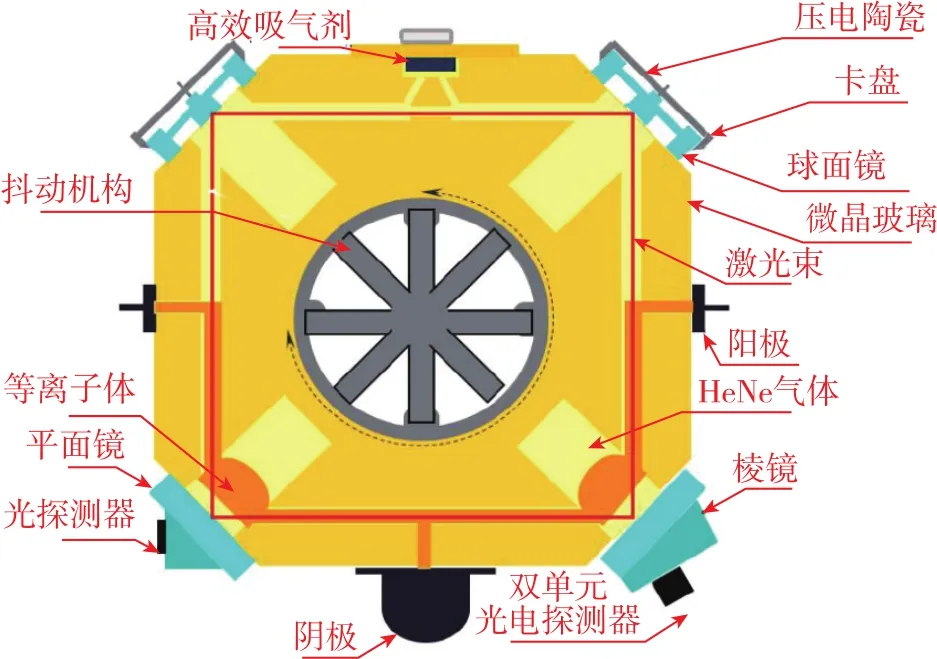
图1 激光陀螺结构Fig.1 Structure of laser gyroscope

激光陀螺本身具有较好的动态性能，但机抖陀螺存在抖动机构，由于陀螺质量分布不均、固定件不对称等因素，动态环境下的抖动机构易发生弯曲变形。如图2所示，OXYZ坐标系为陀螺理想工作坐标系。其中，X轴垂直谐振腔闭合光路，Y轴、Z轴分别过陀螺的阳极与阴极。激光陀螺敏感轴是指垂直于闭合光路等效平面的轴，理想时敏感轴位于X轴，当抖动轴机构弯曲时，陀螺敏感轴随之偏移至X′轴，进而耦合到非敏感方向的角速度，形成测量误差。

图2中，γ即为敏感轴偏移角，可由下式定义

图2 抖动机构弯曲示意图Fig.2 Schematic diagram of dither mechanism bending

式（1）中，βf为与抖动轴弯曲刚度相关的抗弯系数，ainput为输入加速度，其方向与陀螺抖动轴垂直。

机抖陀螺抖动机构弯曲主要由过载造成，由于抖动机构刚度有限，激光陀螺敏感轴垂直方向上的过载加速度可直接造成抖动轴弯曲。振动方面，由文献［4］对某型号陀螺的模态分析可知，如表1所示，其除一阶振型为绕敏感轴X的周期性往复扭转抖动外，其余振型均可造成抖动机构弯曲变形，工程上通过减振器对高频衰减从而避免了激光陀螺的高阶振型。

表1 某陀螺模态分析振型Table 1 Modal analysis of a gyroscope

应对抖动机构弯曲变形带来的敏感轴偏移问题，可通过以下两个角度：

1）提高抖动机构抗弯系数βf： 于旭东等［5］通过对支柱高度、底面厚度和约束位置的优化提高了抖动机构的抗弯强度，但其结构设计带来了体积和质量上的增加，不利于惯性器件的小型化与轻量化设计要求。赵小宁等［1］设计了一种新型四辐条抖动偏频机构，使陀螺的抗振性能提高了4倍多。文献［4］设计了一种双侧固定结构，同时用上下底板固定抖动机构，如图3所示，有效减小了陀螺振前与振中的输出均值差距。

图3 双侧固定结构示意图Fig.3 Schematic diagram of bilateral fixed structure

2）敏感轴偏移的建模与补偿：Kim等［6］理论上推导了高动态情况下激光陀螺敏感轴偏移所造成的漂移，但未进行补偿验证。王林等［7］在此基础上推导建立了陀螺敏感轴动态偏移误差模型，得出了敏感轴偏移造成的附加陀螺漂移与加速度、角速度的耦合关系，如式（2）所示，并通过线振动后的姿态误差角Ф为观测进行辨识，实验验证了补偿后惯导10min线振动的速度误差减少30%以上。与提高抗弯系数βf相比，标定补偿的思路对速度误差的补偿效果更显著，且由于作者在此处采用了工程简化的物理模型与对量测参考意义不做区分的最小二乘估计，随着物理模型与估计方法的改善，补偿精度可进一步提升。

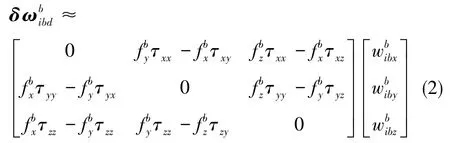
1.2 石英挠性加速度计

石英挠性加速度计由加速度计表头和外围电路组成，包括挠性摆片、传感器（通常采用差动电容）、力矩器、伺服校正检测电路等，其结构如图4所示。

图4 石英挠性加速度计结构Fig.4 Structure of quartz flexible accelerometer

石英挠性加速度计动态误差形成机理为冲击、振动或过载造成的摆片偏移、扭转，如图5所示。其中，图5（a）为正常摆片理想工作状态。在图5（b）中的状态下，摆片离开平衡位置造成差动电容检测非线性与力矩器控制非线性，以前者为例，若摆片具有微小位移Δx，则差动电容ΔC满足式（3）。可见，当Δx≪d0的条件失效时，差动电容检测具有不可忽视的非线性，摆片偏转偏离平衡位置（图 5（b））和摆片扭转（图 5（c））状态均可造成摆片耦合到非敏感轴的加速度。

式（3）中，ΔC为差动电容，Δx为摆片位移，ε为介电常数，A为电容极板面积。

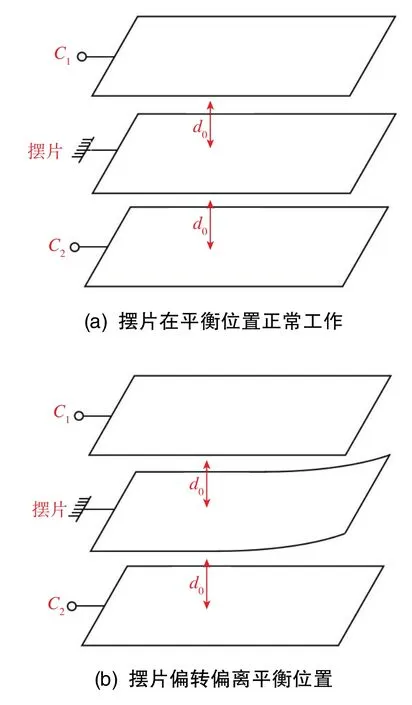
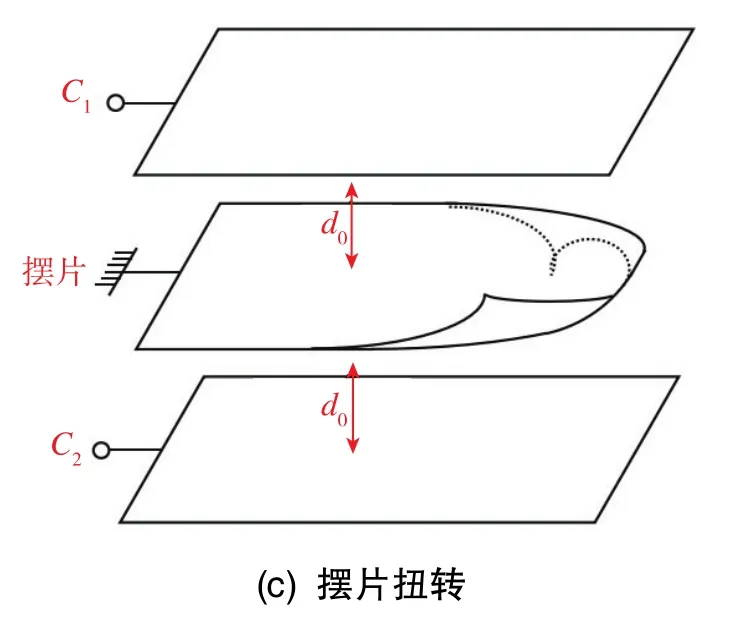
图5 摆片工作状态示意图Fig.5 Schematic diagram of pendulum operating state

解决石英挠性加速度计动态误差，一方面可通过制造与设计控制提高摆片的工作性能，即对上述非线性的误差系数的控制，目前我国对这方面研究较少，仅停留在机理层面上；另一方面可通过对完整模型的非线性误差系数标定实现并补偿。

（1）摆片动态性能机理研究

魏渊等［8］推导了振动环境摆片摆偏角的数学模型，仿真出摆组件质量m、挠性摆有效长度L、阻尼系数c、刚度k、传感器系数Kp、伺服校正网络Gc、力矩器系数Kt等参数对摆偏角α的幅频特性变化规律。肖听雨等［9］利用有限元法对摆片的形变、应力、固有频率、弯曲刚度进行了仿真，并得出其与挠性梁厚度的变化关系。王永建等［10］进行了表头在垂直敏感轴方向加速度下的稳定性实验研究，王春爱等［11］仿真了摆片的各阶固有频率和振型。范达等［12］对摆片偏离平衡位置所造成的差动电容检测非线性进行了补偿，提出了一种利用反函数将系统线性化后再进行校正网络设计的控制方法，使摆片在Δx≪d0条件失效的情况下仍旧与ΔC呈线性关系。

（2）非线性误差系数标定补偿

针对加速度计动态误差形成机理，GJB 1037A⁃2004对摆式伺服线加速度计的完整输出模型给出了定义［13］

式（4）中，U为加速度计输出脉冲，ai、ao、ap分别为加速度计IA轴、OA轴、PA轴的加速度输入，K0为零偏误差，K1为标度因数，Ko、Kp为交叉轴敏感度，Kio、Kop、Kpi为交叉耦合系数，K2、K3为二阶、三阶系数，ε为残余误差。

对式（4）中的K2、K3、Ko、Kp、Kio、Kop、Kpi进行标定补偿，可从单表级标定与系统级标定两个角度展开。

1）单表级标定：重力场标定通常是通过在转台或分度头上的多位置翻滚实验来标定加速度计的，但由于重力场只能提供±1g的加速度激励，其标定的非线性误差在高g环境下往往不再准确，因此需要借助火箭橇、线振动台、离心机进行过载环境标定。

文献［13］、文献［14］给出了加速度计在线振动台上的非线性系数标定方法，但线振动台加速度精度与位置精度不可靠，标定效果差，火箭橇成本昂贵，故基于精密离心机的标定应用最为广泛。

苏宝库等［15］研究了加速度计在单轴精密离心机上的非线性标定方法，并针对实际量测噪声给出了优化设计方案。精密离心机误差对标定精度至关重要，王世明等［16］计算出了单轴离心机误差与加速度计模型系数之间的精度影响关系，并通过线性变换补偿离心机静态与动态误差，得到离心机的精确比力输入，并给出了单轴离心机上的10位置标定方法，如图6所示。

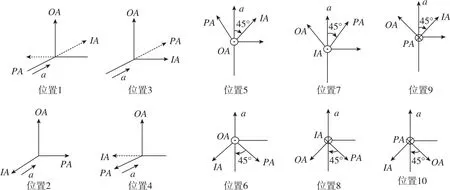
图6 精密离心机10位置标定示意图Fig.6 Schematic diagram of 10 positions calibration by precision centrifuge

双轴离心机为带反转机构的离心机，其反转轴提供与主转轴大小相同的反向角速率输出，其结构如图7所示。双轴离心机的特点为：固定在反转平台上的各点加速度输入均为谐波形式，反转平台上的角速率相对地球转速很小。相比于单轴离心机的优势在于：使用振动整流法消除了加速度计安装误差对标定的影响，由反转轴消除了主轴转动引入的牵连旋转运动，且整个标定仅需安装一次。

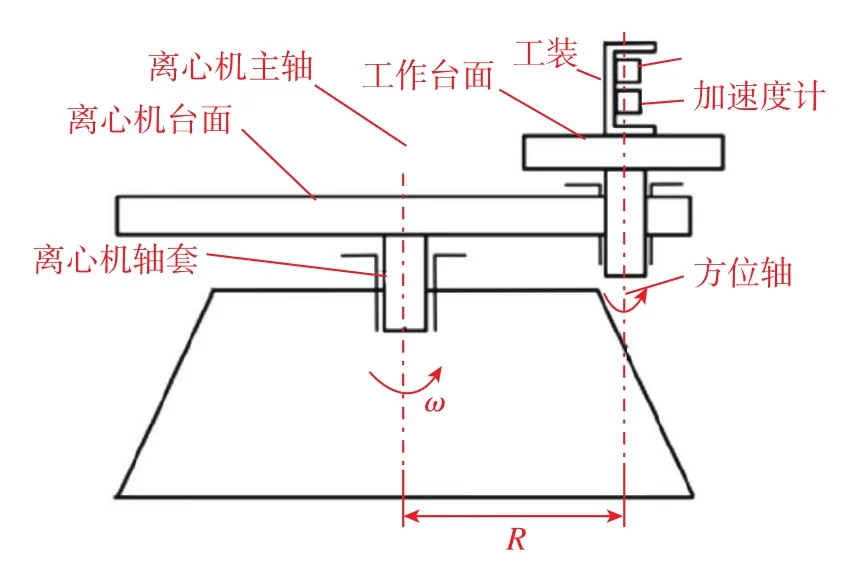
图7 双轴精密离心机结构Fig.7 Structure of double axis precision centrifuge

鲁金瑞等［17］基于双轴离心机精确计算了加速度计三个轴上的输入比力，经过主轴和反转轴正反角位置静态实验以及主轴与反转轴以等值反向的匀角速率转动的动态实验，推导了双轴离心机误差与加速度计模型系数之间的精度影响关系，通过振动整流法精确标定了非线性误差系数。孙闯等［18］在此基础上增加了转速实验，其K2、K3项的标定精度可以达到10-5。

2）系统级标定：以惯导为测试对象，以导航姿态、速度、位置输出为观测估计惯性器件误差系数。

于海龙［19］设计了一种33维的Kalman滤波系统级标定方法，在常用惯导误差参数系统级标定的基础上，在估计模型中添加了加速度计二次项误差系数K2x、K2y、K2z， 通过18次旋转的位置编排激励标定了各项误差，仿真验证了二次项的标定精度优于10-6（g/g2），但受制于标定环境为1g，其标定结果在高g环境下的可靠性有待验证。

唐江河等［20］针对系统级标定1g环境激励不足以及单表级标定高度依赖离心机精度的问题，在平台惯导上设计了利用速度和位置误差积分作为观测的Kalman滤波方法，以低精度离心机加速度作为激励，估计了加速度计二次项，补偿后的速度、位置误差可减小到补偿前的25%，其滤波估计思路可借鉴到捷联惯导。

总体来看，加速度计单表级非线性标定略为成熟，离心机误差修正、噪声处理、误差辨识方法更为完善，而系统级标定存在激励不足、标定局限在K2项上的问题，但二者均存在标定精度无法确定的问题。

2 减振系统动态性能研究

IMU通过减振器与箱体连接，减振器通过其弹性与阻尼特性吸收释放能量来削弱载体的冲击振动，保护惯性器件不被冲击振动损坏，并提供优良的工作环境以保证惯性器件的测量精度。一种常用的惯导减振器如图8所示，通常由金属支座、金属内套和橡胶组成。因橡胶易硫化，具有阻尼大、体积小、质量小和各向刚度同性的优点，且易通过改变橡胶截面尺寸和胶料硬度获得不同的刚度，是惯导减振器最常用的材料。

图8 一种常用的惯导减振器Fig.8 Diagram of a common inertial navigation shock absorber

减振器除隔绝外界恶劣振动环境外，还需要做到：1）衰减机抖激光陀螺的谐振运动：机抖激光陀螺谐振频率常在300Hz～800Hz，并采用低通滤波器实现解抖，其截止频率fc需低于最低的抖频，此时若减振器对IMU对高于fc频率的运动衰减不足，将造成陀螺丢失IMU真实运动信号，对其产生的圆锥与划桨误差也无法补偿；2）减振器各阶谐振频点应避开惯性器件工作频率以保证其工作精度。

2.1 减振器线性建模分析

目前，我国基于线性建模分析的减振器研究与工程应用较为成熟。线性建模分析视减振器弹性恢复力为线性模型，如式（5）所示，又因IMU台体刚度远大于减振器刚度，视IMU为具有六自由度的刚体。在不考虑阻尼影响与小位移假设的条件下对模型进行简化，图9即为一种八点减振的简化模型。

式（5）中，F为减振器弹性力，k为减振器刚度，Δl为弹性位移量。

图9 八点减振简化模型示意图Fig.9 Schematic diagram of simplified eight points damping model

基于对动力学微分方程的推导、求解、仿真与振动冲击实验，学者们在以下角度展开了充分的研究：减振器的布局方案优化［21⁃22］、振动耦合机理与解耦［23⁃25］、 线角振动固有频率分析［26］、 减振器与箱体结构参数对惯导精度影响［27］等，图10即为工程中常用的减振器布局。总体来看，基于线性建模分析的减振器设计能基本满足各类惯导在静态和低动态环境下的工作要要求。

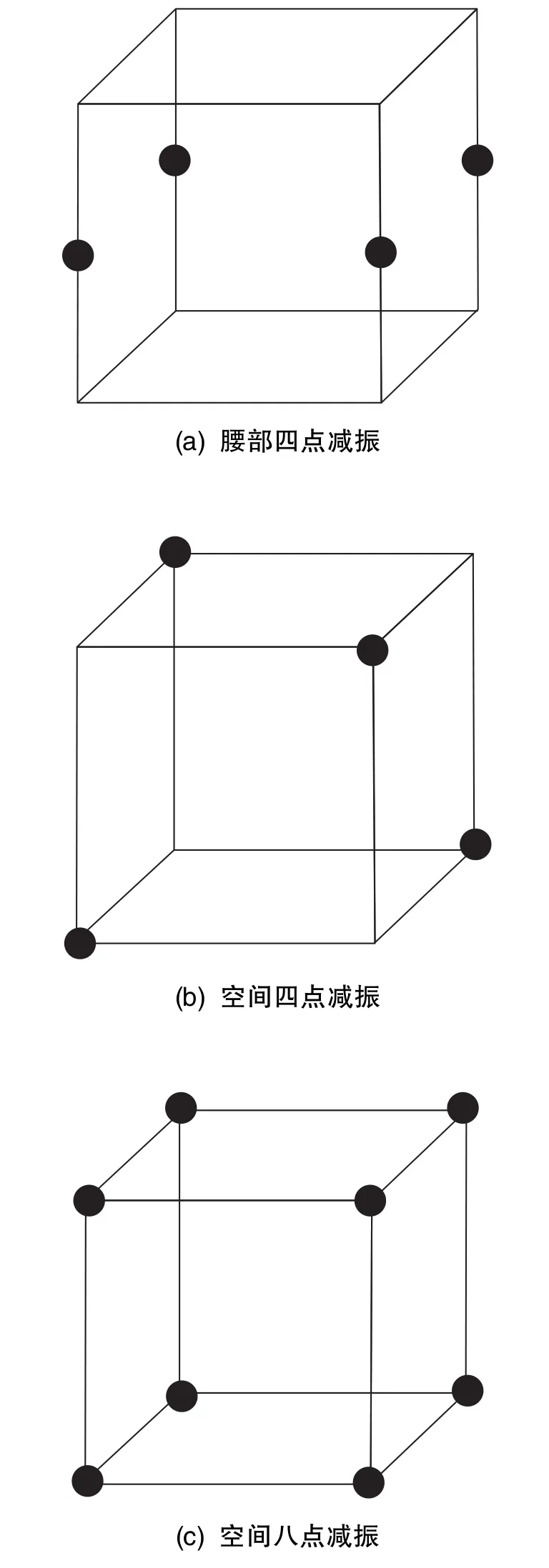
图10 工程中常用的减振器布局Fig.10 Layout of shock absorbers commonly used in engineering

2.2 减振器非线性建模分析

（1）动态刚度非线性

动态刚度非线性是指：惯导在实际高动态环境中所受外界激励幅值大，减振器变形不再满足线性分析时的小位移假设，此时减振器的刚度是高度非线性的，即具有渐软或渐硬特性。文献［28］用有限元对单个减振器施加力载荷，发现其刚度随位移的增加而增加，即具有渐硬特性，如图11所示；文献［3］则把惯组通过减振器连接在振动平台上，并发现随着正弦激励振幅的增加，系统传递特性的峰值频率减小，说明其刚度随之减小，即减振器具有渐软特性，如图12所示。由此可见，惯导在实际高动态环境中工作时，小位移假设失效，按照线弹性假设设计的减振系统不再具有可靠性。

图11 减振器刚度位移图Fig.11 Stiffness displacement diagram of shock absorber

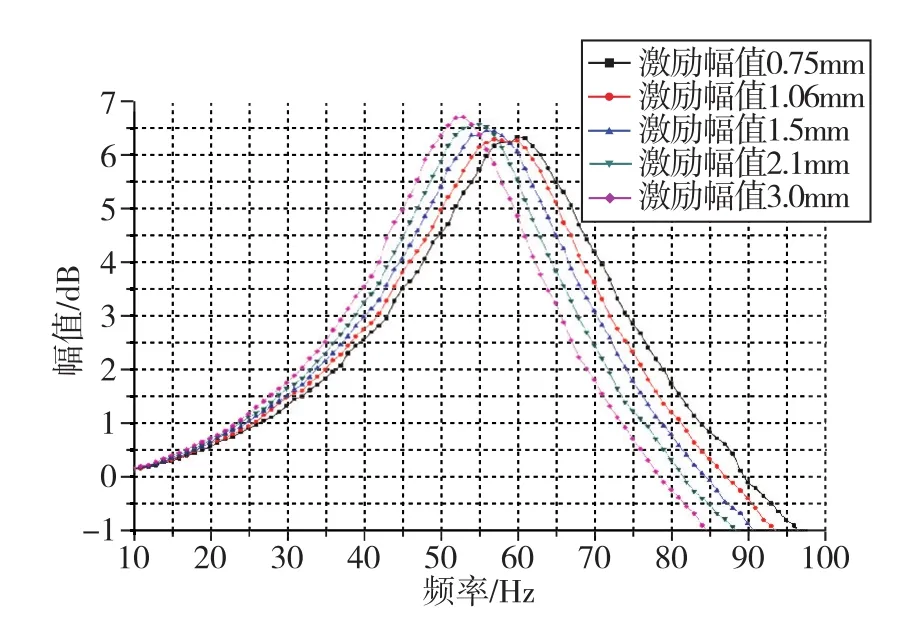
图12 惯导传递特性图Fig.12 Diagram of inertial navigation transfer characteristic

有学者针对单一橡胶减振器的非线性展开研究，王丹等［28］根据实验得到的减振器恢复力⁃位移迟滞曲线研究了频率、动态位移幅值对橡胶减振器的动刚度的影响规律，并通过最小二乘法对非线性恢复力模型进行了参数辨识；孙伟等［29］提出了减振器的非线性动力学模型及求解方法，仿真计算了减振器的动态响应；张鹏飞等［30］则基于奇异值分解的复解析小波脊线提取方法标定了减振器的非线性模型，该方法能有效减少噪声的影响。

虽然标定方法各异，但其拟合得到与实验验证的减振器弹性恢复力模型统一，即由线性弹性力、三次非线性弹性力以及一次黏性阻尼力组成

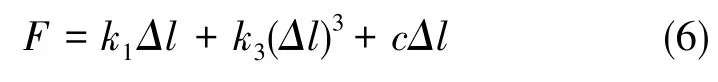
式（6）中，F为减振器弹性力，k1、k3、c为待识别的刚度和阻尼系数，Δl为减振器形变（位移量）。

基于式（6）的减振器非线性模型，学者们对惯组整体进行了非线性建模分析研究。商霖等［3］建立起惯组的非线性动力学模型，求解出系统的非线性频响函数和传递特性，并通过扫频实验验证了非线性模型的准确性。付玮等［31］推导了在基础激励下的惯组非线性运动微分方程，并发现在单自由度实验下可实现解耦的减振系统，在多自由度工况下由于显著激发了减振器非线性的渐软特性而发生了多自由度的耦合。

（2）温度刚度非线性

温度刚度非线性是指：减振器在温度变化时，橡胶材料的链段运动变化导致橡胶材料模量改变，减振器刚度随之发生非线性变化，并导致减振器系统谐振频率与放大倍数的改变。

为研究高低温环境下减振器的动态性能变化，往往需要在温度振动综合实验箱中进行复杂实验，因此学者们考虑研究温度与振动特性的规律。低温方面，郭瑞毅等［32］将压剪混合型减振器安装在测试工装上，并将工装安装在振动台上，在不同的低温下输入正弦激励并记录振器的谐振频率与放大倍数，如图13所示。可见，减振器谐振频率在100℃的温差范围内变化高达70Hz，其拟合的减振器谐振频率模型如式（7）所示，对三种邵氏硬度不同、结构不同的减振器进行拟合，并通过-45℃的实验验证了模型拟合误差均在5%以内。高温方面，王丰等［33］对几种T型减振器做了温度研究，由图14可知，谐振频率在80℃的温差范围内变化了20Hz，其拟合出的模型如式（8）所示，其与温度为二次关系，实验也验证出了模型拟合误差可控制在5%以内。郭瑞毅等［34］以类似思路研究了压剪混合型硅橡胶减振器的振动冲击性能与温度的关系，研究可知，结构相同的减振器拟合模型相似，拟合效果较好，通过拟合结论设计减振器可节省大量实验时间。

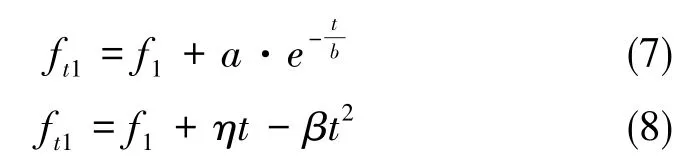
式（7）、 式（8）中，ft1为减振器温度t下的一阶谐振频率，f1为与温度无关的频率常量，a、b、η、β为与减振器结构和橡胶性质有关的温度敏感系数。

图13 低温谐振频率与放大倍数的规律Fig.13 Law of low temperature resonant frequency and magnification

图14 高温谐振频率与放大倍数的规律Fig.14 Law of high temperature resonant frequency and magnification

总体来看，目前我国工程上依旧采用线性假设下的减振系统设计，相关的研究也较少，无论是谐振频点改变而产生共振破坏IMU或惯性器件，或是振动耦合带来的严重圆锥运动与划桨运动，都严重降低了惯导的动态可靠性。

3 导航算法动态精度研究

捷联惯导导航算法在高动态环境下的解算误差主要来自于姿态算法与速度算法。圆锥运动是指：载体的两个相互垂直的输入轴有同频但不同相位的正弦角振动时，与它们垂直的第三轴会产生圆锥运动，并具有常值角速度，如图15所示，其中的α即为半锥角；划桨运动是指：载体的两个相互垂直的输入轴有同相角振动和线振动时，其第三轴就会产生划桨运动，并具有常值速度。圆锥运动与划桨运动最大程度地激发了矢量积分的不可交换性误差，因此成为验证算法性能的典型运动。在惯性器件输出均为增量时，划桨误差补偿算法与圆锥误差补偿算法具有对偶性［35］，划桨补偿可直接套用圆锥补偿的系数，因此本文仅讨论姿态算法。

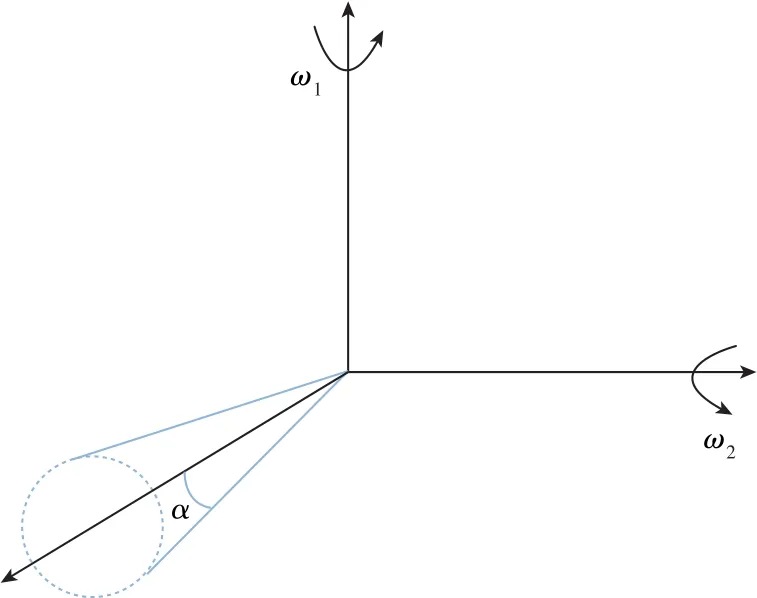
图15 圆锥运动示意图Fig.15 Schematic diagram of coning motion

为解决姿态算法在对角增量矢量离散积分时产生的不可交换性误差，Bortz［36］于1971年提出的等效旋转矢量法可有效解决不可交换性误差，Bortz微分方程如式（9）所示。 1983 年，Miller［37］给出了三子样最优性能圆锥算法。主流的等效旋转矢量多子样算法将式（9）等号右端第二项的Φ近似为角增量，如式（10）所示，并视式（9）右端第三项为Φ的二阶小量直接忽略，按式（11）求解Bortz方程。该方法在一个积分周期内对角增量多次采样计算等效旋转矢量，再由等效旋转矢量计算姿态更新四元数，其过程如图16所示。

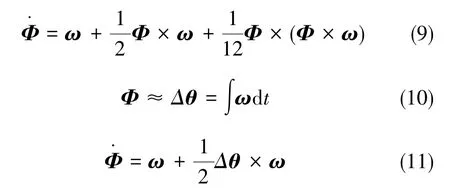
式（9）～式（11）中，Φ为等效旋转矢量，ω为载体相对于导航系的角速度，Δθ为一个积分周期内角增量。

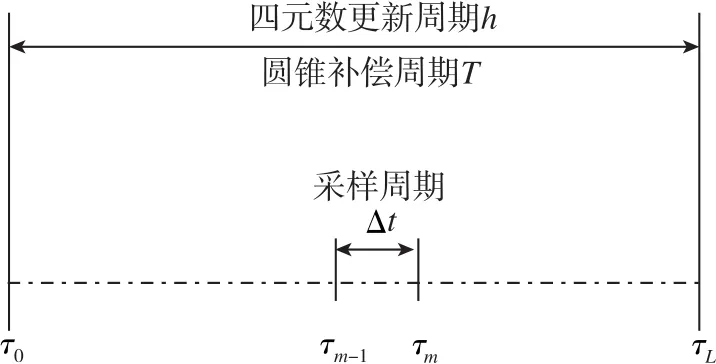
图16 等效旋转矢量算法示意图Fig.16 Schematic diagram of equivalent rotation vector algorithm

提升算法精度有以下三种途径：

（1）提高算法子样数

继Miller三子样算法，很多学者通过增加算法子样数N来增加角速度拟合阶次［38］，补偿残余误差如式（12）所示。由此可知，理论上静态环境下子样数N越高，圆锥误差补偿精度也就越高。然而，多子样算法的推导是基于半锥角α为小角的假设，高动态下的大锥角锥运动或大角度机动时，α不再是可忽略的小角。严恭敏等［39］推导了α半锥角产生影响时的残余误差，如式（13）所示，通过计算发现：当α仅为0.1°时，N高于4时算法精度就受限于α，子样数增加不但不能提高精度，反而会因姿态更新频率降低而精度更差。

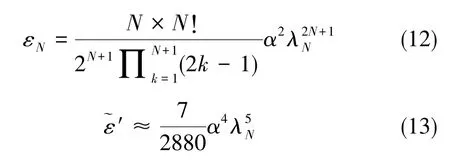
式（12）、 式（13）中，N为子样数，α为半锥角，λN＝ΩT，Ω为锥动周期，T为积分周期。

（2）多项式迭代求解

相比提高算法子样数的直接求解，通过数值法求解Bortz方程可从原理上避开近似误差。严恭敏等［40］则通过多项式迭代对Bortz微分方程进行数值求解，迭代收敛快且计算负担没有增加。在此基础上，刘锡祥等［41］通过增加圆锥约束提高了拟合阶次。文献［42］、文献［43］也通过多项式迭代法求解，区别为其分别使用四元数微分方程和罗德里格参数微分方程作为数学工具。尹剑等［44］提出了单次、多次利用前周期采样信号，在没有牺牲姿态更新频率的基础上增加了拟合阶数。

（3）补偿三重叉积

王茂松等［45⁃46］考虑了补偿 Bortz 微分方程的三重叉积项， 即式（9）等号右端的Φ×（Φ× ω）项来提高补偿精度，增加了角增量的三阶和四阶叉乘项并推导了其补偿系数，因推导过程复杂，故难以拓展到五阶。

总体来看，惯性器件与减振系统在控制动态误差中占据主导地位，目前惯性器件在动态环境下的误差仍高于算法精度的（数量级上），而只有高精度的数据源才能发挥高精度算法的优势。

4 总结与展望

激光捷联惯导为高精度的复杂系统，其内部的惯性器件、机械结构、转动机构、减振器、密封、软件电路等均可受高动态环境影响，提高其动态精度需要多学科交叉、长周期、高成本的研究投入。未来我国惯导的高动态研究除文中提到的关键问题外，也可考虑以下思路：

1）惯导温控：我国目前针对加速度计与激光陀螺的温补研究成熟，已在激光捷联惯导中广泛应用，由于减振器并非是测量器件，无信号输出，不能应用相同的温补思路，因此考虑对惯导内部进行温控，可极大提升惯导在极寒地区与高温环境下的动态可靠性。

2）频域导航：频域导航算法通过将角增量与速度增量转换到频域结算，在补偿不可交换性误差方面优于时域算法，其缺点为计算量大、实时性较差，随着芯片计算速度的不断提升，频域导航成为了可能。刘鑫宇等［47］给出了频率解算的一般方法，并验证了频域导航在100s内的姿态误差优于时域算法1个数量级。

3）研究机抖陀螺抖动影响：受制于加工精度，实际激光陀螺的抖动轴与敏感轴无法重合，导致机抖陀螺在绕抖动轴微幅往复抖动时，敏感轴绕抖动轴做微幅锥动，这种锥动带来的误差在陀螺谐振腔因过载或振动而发生变形时被放大。

4）研究激光陀螺角加速度影响：包括文献［7］在内对激光陀螺敏感轴动态偏移进行分析时，仅考虑了惯性力的影响，由于实际惯导工作环境存在复杂的角振动，本体的配平误差与减振器不对称导致的振动耦合也将导致剧烈的角振动，在动力学分析时考虑角加速度的影响很有必要。