自抗扰控制在陀螺加速度计伺服回路中的应用

王兆凯，王 汀

（1.超精密航天控制仪器技术实验室，北京 100039；2.北京航天控制仪器研究所，北京 100039）

0 引言

导航系统依靠陀螺加速度计敏感载体的加速度得到载体的速度和位置信息，从而实现整个导航系统的功能。陀螺加速度计作为导航系统的核心器件，其正常工作必须要有相应的伺服回路来保证，从而保障仪表的动态性能和稳定性［1］。

现阶段的陀螺加速度计伺服回路主要采用基于经典控制理论的设计方法，即针对表头特性确定回路参数，匹配出满足要求的校正网络。该方法虽然可以满足工程需求，但遇到非理想陀螺加速度计系统时不能很好地处理仪表本身不确定因素对系统的影响，导致仪表精度无法进一步提高，参数摄动、环境条件变化等不确定性因素都会极大地影响回路性能［2］。因此，本文将在数字控制系统的基础上对伺服回路进行控制算法设计，从而减小不确定因素对系统的影响，提高仪表的精度和稳定性。

自抗扰控制技术汲取了传统PID控制器 “以误差消除误差”的思想精华，是在改进PID控制器固有缺陷的过程中逐渐发展而来的一种新型控制技术。它不依赖于系统模型，是一种低超调、收敛速度快、精度高、抗干扰能力强、算法简单的新型非线性控制器。它将由系统内扰动引起的内部扰动和因外部环境等引起的外部扰动统称为总扰动，通过扩张状态观测器和非线性状态误差反馈控制律两个环节对总扰动进行实时估计并加以补偿。在控制律部分，加快系统收敛速度从而实现非线性系统的近似线性化，以提高控制器的控制品质和控制精度。它不要求对象的精确模型，同时根据被控对象整定控制器参数，并通过已知的系统输入输出来实现最终的控制效果［3］。本文将介绍陀螺加速度计稳定回路的自抗扰控制方法，并给出仿真与实验结果。

1 陀螺加速度计的数学模型及误差来源

陀螺加速度计伺服回路由仪表传感器、前放电路、功放电路和无刷力矩电机组成。仪表传感器输出电压信号，经过前放电路的交流放大、相敏解调、低通滤波，输出到功放电路中；再经过校正网络、比较电路，将直流电压信号调制成脉冲调宽信号，结合逻辑变换电路，经功率电路输出电流到力矩电机，控制电机输出力矩，平衡仪表的外环摩擦力矩，保证仪表正常工作。

（1）陀螺加速度计传递函数的推导

三浮陀螺加速度计的伺服系统由作为控制对象的三浮陀螺加速度计和保证仪表正常工作的伺服回路组成，陀螺加速度计的控制系统框图如图1所示［4］。

图1 陀螺加速度计系统框图Fig.1 Block diagram of PIGA system

图1中，ax1为仪表沿外框架轴的输入视加速度；ml为仪表绕内框架轴的摆性；H为仪表角动量；Mx1为绕外框架轴的各干扰力矩之和；MD为电机的力矩；K0为电子部分的增益；G（S）为校正网络传递函数，且G（0）＝1；Jx1、Jy分别为外框架组件绕x1轴和内框架组件绕y轴的转动惯量；Cy为绕内框架轴的阻尼系数。

图1所示的陀螺加速度计系统，其传递函数为

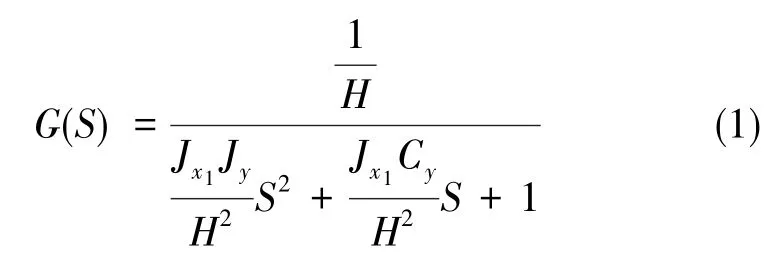
（2）陀螺加速度计系统的误差来源与处理方式

在仪表的实际应用过程中，其动态精度与振动谱能量大小、仪表是否存在谐振点、仪表结构刚度特性、轴系的垂直度、伺服系统参数设计等多种因素有关。其中，由于受型号要求和表头结构设计等约束，伺服回路调整以外的影响因素属于难以进行调整的环节，因此通过调整伺服回路，减小内环偏角β成为提高振动精度的主要手段。

本文主要通过伺服回路算法进行设计，根据系统带宽整定控制器参数，从而提高系统的动态刚度。通过增大系统阻尼、减小浮子的运动幅度，来达到减小仪表内环偏角β的目的，进而增加系统的抗振性，改善仪表性能。

根据仪表模态和力矩电机工作特性，结合对惯性导航平台飞行试验过程中陀螺加速度计输出数据的分析，可以确定陀螺加速度计伺服系统的带宽，由此可以得到满足系统带宽要求的PID控制器，并以此为基础进行自抗扰控制器的设计工作。

2 自抗扰控制器的设计

对于一个二阶系统［5］，有

式（2）中，u为控制量，y为系统输出，w（t）为系统扰动，b0为由系统特性决定的常系数。该系统对应的自抗扰控制器结构如图2所示。其中，跟踪微分器在安排过渡过程的同时提取各阶微分信号，扩张状态观测器通过输出y来估计观测对象所有不确定因素和外扰作用的总和，安排的过渡过程用来形成控制信号u，该控制信号通过对象状态估计量之间误差的适当非线性组合和未知扰动量的补偿实现。当以上三个环节中的非线性函数和参数选择恰当时，即可实现良好的控制效果［6⁃7］。

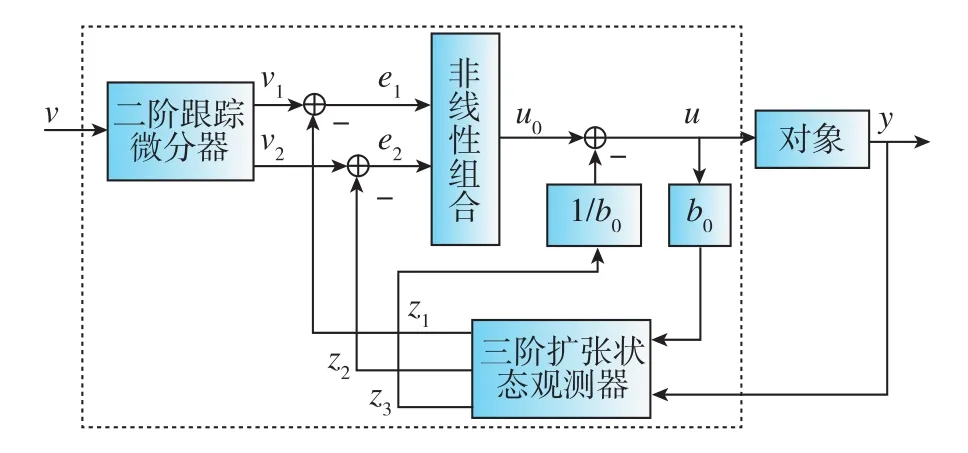
图2 自抗扰控制器结构图Fig.2 Structure diagram of ADRC

（1）跟踪微分器（TD）

跟踪微分器由设定值（目标值）v和对象允许的过渡时间T0来确定，v1（t）为过渡过程，v2（t）则是该过渡过程的微分信号。该环节参数为速度因子r和滤波因子h，滤波因子h根据经验确定，跟踪微分器对输入信号的跟踪速度与速度因子r的大小有关［8］

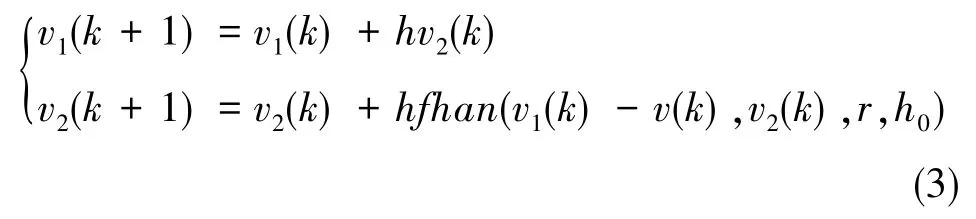
该环节中，fhan（）定义如下

且a的定义为

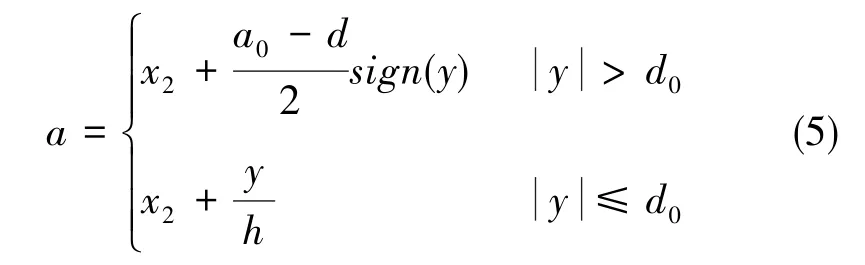
（2）扩张状态观测器（ESO）

将系统所有不确定模型和外扰作用扩充为新的状态变量，通过非线性反馈效应抑制其作用，则状态观测器可构造为

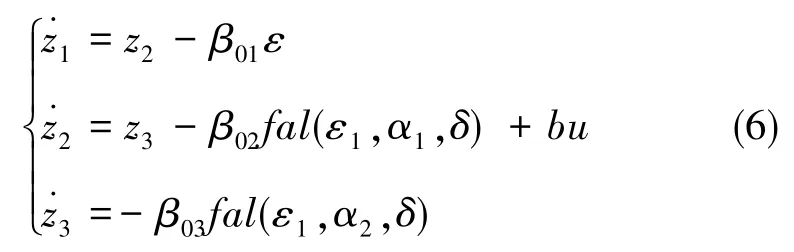
z3（t）为被扩张的状态量，用于估计对象的所有不确定模型和外扰动；α1、α2与β01为可变参数。其中，α1、α2可根据经验确定。β01、β02、β03与采样时间T存在如下经验公式

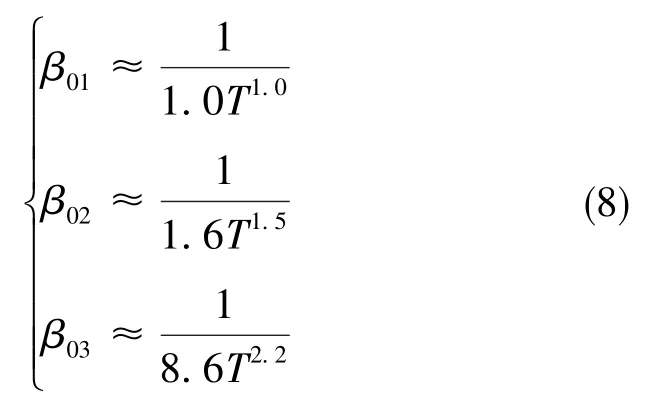
根据采样时间初步确定三个参数后，通过进一步仿真优化， 可以得到β01、β02、β03的最终取值［9］。

（3）非线性状态误差反馈控制律（NLSEF）

采用非线性组合的方式构成控制器，能对系统的误差实现有效的控制，同时还能抑制系统中的不确定性扰动。通过将跟踪微分器产生的跟踪信号、微分信号与扩张状态观测器对系统各状态变量估计值求差，得到误差量后结合fal函数与扩张状态观测器对总扰动的补偿量来产生系统的控制量，其表达式如下

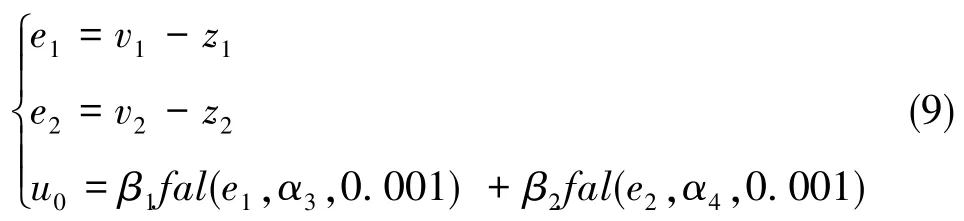
为实现扰动补偿，再将系统总扰动z3前馈到控制量，形成被控对象的实际控制量

该环节中，β1和β2采用满足系统要求的PID控制器中比例环节系数Kp和微分环节系数Kd，α3、α4、b0为待整定参数。根据相关资料和大量仿真经验，b0取值范围为［0.01，10］。通过对不同参数进行仿真，可以最终确定三个参数的取值。

（4）自抗扰控制器设计结果

综上所述，TD、ESO和NLSEF三部分构成了一个完整的自抗扰控制器。跟踪微分器（TD）负责对系统的过渡过程进行处理，对输入的指令信号进行柔化，并提取高质量的微分信号，可以较为有效地解决系统超调问题；扩张状态观测器（ESO）作为自抗扰控制器的核心组件，在对被控系统的状态进行实时、有效预估的同时，对被控对象的总扰动进行实时估计并给予补偿；非线性状态误差反馈律（NLSEF）采用误差的非线性组合的方法，形成的控制量用于对系统非线性误差的有效控制，同时还能对被控对象的不确定扰动进行较好地抑制与调节。经以上环节，可将控制器参数整定如下，如表1所示。

汉晋之际是中国艺术史上的关键阶段，艺术在这一时期摆脱了“名教”和经学的束缚，文人士大夫的热衷参与促进了艺术的高度繁荣。特别值得一提的是，汉晋之际以琅邪王氏和陈郡谢氏为代表的江南艺术世家对艺术发展和传承的作用和影响尤为突出。由于江南艺术世家的贡献，这一时期，音乐、书法、园林、诗歌等艺术领域获得了全面的繁荣，不仅极大地提高了当时艺术创作与品评的水准，而且为后世艺术的传承与革新提供了重要的借鉴和指导。

表1 自抗扰控制器参数整定结果Table 1 Tuning results of ADRC parameters

3 系统仿真

通过Matlab软件中的Simulink模块对所设计的自抗扰控制器进行仿真，以观测其性能。根据自抗扰控制器理论模型，将控制器代入陀螺加速度计系统框图中，结合已确定的控制器各环节参数，在Simulink中建立系统模型。

现阶段，仪表伺服控制主要通过根据表头特性匹配校正网络的方法实现，其传递函数为

将自抗扰控制器与原校正网络放于同一模型中，并引入同一输入信号，将输出结果进行对比，建立如图3所示的Simulink模型。

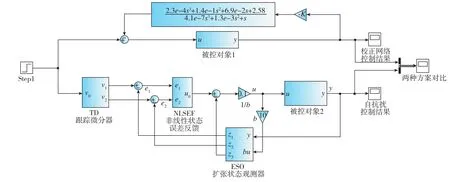
图3 系统的Simulink模型Fig.3 Simulink model of PIGA system

该模型中，采样时间设置为2kHz。本文分别通过阶跃和正弦两种输入信号对系统进行仿真，考察不同控制方法下系统输出信号的特性。同时，考虑到在实际情况中，当仪表工作温度升高时，仪表内部浮油的黏性会降低，浮油的特性变化将导致仪表内框架阻尼系数Cy发生变化，进而影响仪表性能［10］，故本文还考虑了仪表内框架系数发生改变后的情况，并与正常条件下的仿真结果进行了对照。

（1）阶跃输入下的仿真结果

阶跃输入下的仿真结果如图4所示。

图4 两种控制方案下的系统阶跃响应Fig.4 Step response of PIGA system under two control schemes

可以看出，在给定阶跃输入下，自抗扰控制方法与原校正网络相比调节时间更短且超调量很低，控制效果更好。

将仪表内框架系数减小15%，再通过两种控制方案进行仿真，如图5所示。由仿真结果可知，参数发生变化后，自抗扰控制方法稳定性较强，而原校正网络则出现了较为明显的超调现象。因此，自抗扰控制方法削弱了温度变化对仪表的影响。

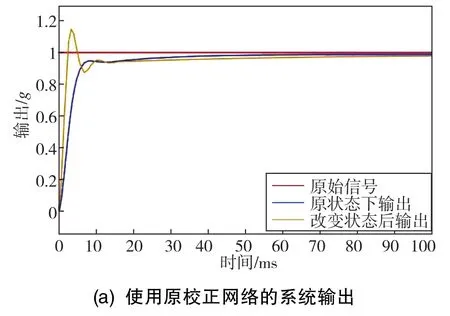
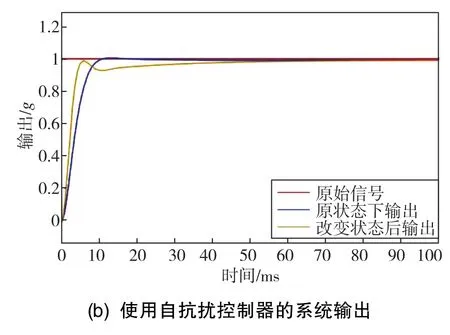
图5 改变温度后的系统阶跃响应Fig.5 Step response of PIGA system after changing temperature

（2）正弦输入下的仿真结果

本文中，仪表的系统带宽为90Hz。为考察自抗扰控制方法在带宽范围内的工作特性，将输入信号更换为频率为90Hz的正弦信号后，重新进行仿真，仿真结果如图6所示。

图6 两种控制方案下的正弦输入系统响应Fig.6 Sinusoidal input system response under two control schemes

可以看出，受90Hz的输入信号作用之后，两种控制方法下的系统输出均表现出了一定程度的相位滞后和幅值衰减现象，但是采用自抗扰控制方法的系统其输出信号变化程度更小。

同时，针对该正弦输入信号，本文也在改变被控对象中内框架阻尼系数Cy后采用两种控制方法进行了仿真，如图7所示。在状态改变之后，自抗扰控制方法下的系统表现出了更好的稳定性，虽然相位滞后和幅值衰减的程度均有所增加，但整体变化幅度小于校正网络控制下的系统。

图7 改变温度后的正弦输入系统响应Fig.7 Sinusoidal input system response after changing temperature

由以上仿真结果可以看出，本文设计的自抗扰控制器相比于仪表原有的控制手段具有较为优良的性能。接下来，将通过仪表的静态和动态实验进一步验证本文的自抗扰控制方法对仪表输出精度的影响。

4 仪表精度实验

为验证所设计自抗扰控制器的实际应用效果，本文还进行了配表的静态和动态实验。通过在DSP2812开发板上烧写控制器程序，实现仪表的自抗扰控制，并将实验结果与传统控制方法下的仪表输出精度进行了对比。

（1）静态实验

按照仪表的技术条件要求，本文采用六位置翻滚实验考察仪表的静态精度。六位置实验以仪表X轴朝上记录为起始点（0°），依次向北在垂直平面内绕分度头转轴翻转，在0°、 60°、 120°、 180°、240°、300°六个位置上测量加速度计的输出数据并进行结果计算，通过考察仪表处于不同位置时对误差系数K0、K1的标定结果，判定仪表的一致性。两种方法下，归一化处理之后仪表六位置翻滚实验的精度结果如表2所示。

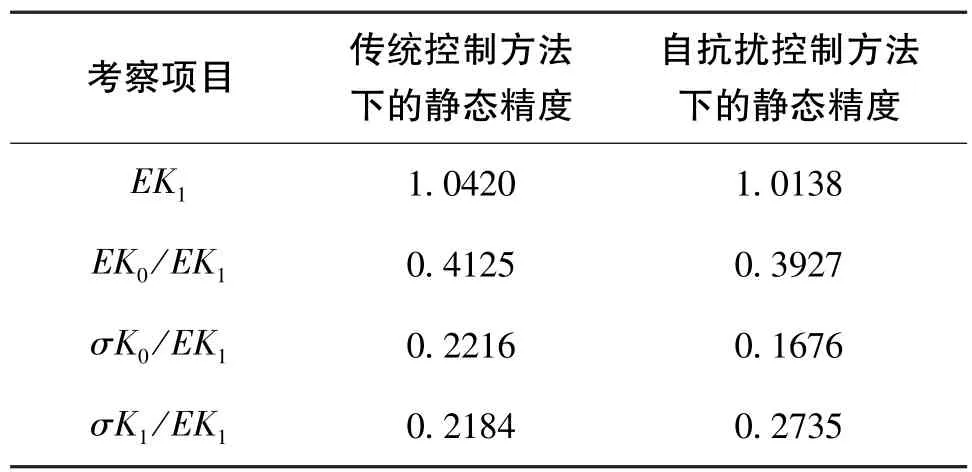
表2 静态实验结果Table 2 Results of static experiment

由表2可知，由于静态条件更接近仪表的理想工作环境，故两种不同方法下仪表的精度相当，均满足六位置实验对仪表输出精度的要求。但是，由于静态条件下仪表工作性能较为稳定，故六位置翻滚实验没有体现出两种控制方法的差别。

（2）动态实验

为了进一步验证自抗扰控制器的性能，后续又进行了模拟严苛工作环境的随机振动实验。随机振动实验采用统一振动功率谱（频率范围为20Hz～2000Hz， 均方根加速度RMS＝4.4g0）， 每次振动时间为2min，通过对振前与振后、振中的数据处理得到振动精度。考虑到仪表内框架阻尼系数Cy会随温度变化而变化，本文通过更改仪表工作温度，探究不同控制策略下仪表在温度改变前后的精度变化，最终得到的振动精度结果经归一化处理后如表3所示。

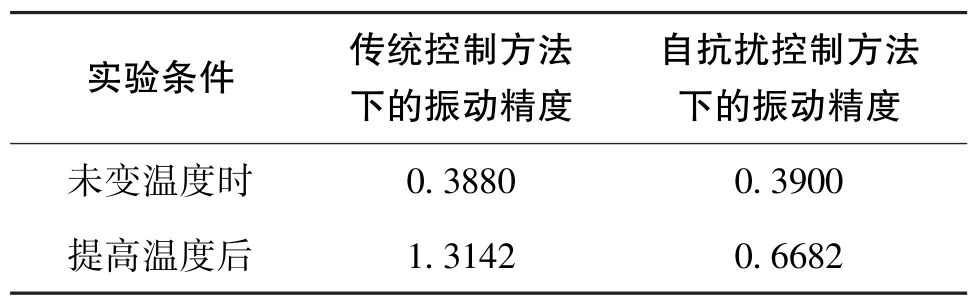
表3 传统控制方法与自抗扰控制方法的配表振动精度对比Table 3 Comparison of vibration accuracy between traditional control method and ADRC method

由表3可知，在文中给定的振动条件下，未改变温度时两种控制方法下的振动精度基本相当；而提高温度后，自抗扰控制方法下的精度变化幅度为71.32%，采用传统控制方法的精度变化幅度为238.70%。可见，采用自抗扰控制方法后，仪表的稳定性有所提高。

5 结论

基于数字控制系统，本文采用自抗扰控制方法改善了仪表伺服回路性能，并通过仿真和实验对所设计自抗扰控制器的性能进行了验证。结果表明，在保证仪表动态、静态精度的前提下，自抗扰控制方法削弱了温度变化对仪表输出精度的影响，可在工程实际中进行进一步的应用。