强磁场中的Li原子

刘凤丽

(黑龙江大学 物理科学与技术学院, 哈尔滨 150080)

0 引 言

迄今为止，人们已经观测得到的白矮星有1 000多颗，借助于光谱分析，其中有600多颗被划分为磁化了的白矮星。由于对磁场中原子的理论研究数据的匮乏，只有40%左右的白矮星的磁场被确定下来。白矮星或中子星的磁场或电场的确定对于研究星体的演化十分重要，磁场或电场的大小需要通过研究分析星体的光谱确定，而不同磁场下的不同原子态的原子结构的理论研究数据对于研究星体光谱非常必要。除了天体应用的需要，强磁场中原子的研究也是基础物理研究的兴趣所在。事实上，磁化的白矮星给物理学家提供了一个天体实验室，用来检验物理学家提出的研究磁场中原子的动力学理论和数值计算方法的正确性。

1970年，Kemp等首次确定出白矮星GRW+70.8247中存在被磁化的星体[1]，人们对磁化的白矮星的研究产生了浓厚的兴趣，更引起一批物理学家关注磁场中原子结构的研究。1977年，Garstang研究了在白矮星强磁场范围的H原子、He原子以及碱金属原子的塞曼效应[2]。2015年，Ferrario等通过光谱研究确定了单体和双体白矮星的磁场大小[3]。在过去的几十年，尽管人们作了很多的努力来研究磁场中的原子，然而所用理论和计算能力仍然满足不了对天体光谱的模拟研究，尤其对处在白矮星的强磁场数量级中复杂原子结构的研究更为困难。近几年，随着人们的不断努力，从理论上的修正、数值计算方法和计算机性能的提高对强磁场中的原子结构研究取得了一定的进展。人们对强磁场中H原子结构和光谱的研究比较成熟。1984年，Rösner等在建立了多组态混杂的Hartree-Fock方法计算了在白矮星和中子星磁场范围的H原子的结构，给出了31种基态和低激发态的能级、不同线系的波长、偶极强度、振子强度和跃迁速率等信息[4-5]。接下来几年，Baye等几个课题组通过建立不同的理论方法解决了强磁场中H原子的基态和低激发态的能级问题[6-8]，但却发现不能同时解决H原子的高激发态的结构问题。近几年，Wunner[9]和Zhao[10-11]等发展了二维有限元方法解决了这个问题，给出大量的H原子态的能级，计算了这些态之间的跃迁光谱数据。

与H原子不同，对于强磁场中多电子原子的结构和光谱很少见报，主要原因是很难处理电子关联问题。1999年，Becken 等研究了强磁场中的He原子，该项研究被视为处理电子关联问题的里程碑[12]。之后，Guan等课题组给出几篇关于磁场中的Li原子的研究报告，处理了Li原子中电子关联问题[13]。本课题组在前人的理论基础之上，对Li原子采用模型势，改进了技术手段，使得新的理论和计算方法不仅适用于基态和低能级的Li原子结构，还适用于高激发态的能级计算，同时大大减少了计算机时并提高了计算精度，提供了在白矮星磁场范围的5种原子态ν20+，ν20-，ν2(-1)+，ν2(-1)-和 ν2(-2)+(ν = 1-10，ν代表原子态的序列号)的能级以及高能级向低能级跃迁的光谱数据[14-15]。在前期工作基础上，在柱坐标系下，本研究利用二维B-spline方法，进一步研究强磁场中的Li原子更高激发态1320-和132(-2)+的结构、几率密度随磁场的变化规律，该研究结果有助于进一步理解原子中电子的运动行为。

1 计算方法

(1)

式中：ρ、φ和z是柱坐标系的三个坐标变量；V(ρ,z)是McMillan给出的模型势，具体形式如下：

(2)

由边界条件可知：

(3)

体系的哈密顿算符的本征波函数以二维B样条Bi,k为基函数[15]，则波函数的表达式为：

(4)

式中k为Bi,k的次序，由于本文k不会引起B样条的混淆，因此，本文省略下角标k。将式(4)代入定态薛定谔方程中，即被式(1)作用，得到以下矩阵方程：

HC=ENC

(5)

式中：H为哈密顿算符的矩阵表示；E为Li原子的能量；N为重叠矩阵。哈密顿算符的矩阵元表示为：

(6)

由于B样条基函数不归一化，所以存在重叠积分N：

(7)

将式(6)、式(7)代入式(5)，于是求解矩阵方程式(5)，即可得到Li原子的能级和对应的波函数。

2 计算结果与讨论

表1 不同磁感应强度下Li 原子的三个原子态13 20-、13 2(-2)+ 和 2 2(-2)+的能级

当磁场为零时，1320-、132(-2)+和 22(-2)+分别对应Li原子的1s29p2P、1s29d2D和1s24d2D原子态，对磁量子数m是简并的，因此，表1给出的是在无磁场时的三个能级1s29p2P、1s29d2D和1s24d2D在强磁场中发生塞曼效应对应的1s29p2P0、1s29d2D-2和1s24d2D-2三个能级随磁感应强度的变化情况。从表1可以看出，零场时此三个能级与NIST 数据库给出的实验值十分吻合，例如计算得到的1s24d2D态的能级为-3.126 0(-2)a.u.，实验值为-3.127 3(-2)a.u.；计算得到的1s29p2P态的能级为-7.909 8(-3)a.u.，实验值为-7.9074(-3)a.u.；计算得到的1s29d2D态的能级为-6.174 0(-3)a.u.,实验值为-6.177 5(-3)a.u.。因此可认为本文给出的研究强磁场中的Li原子的计算方法和计算结果为可信赖的。

图1给出了1320-、132(-2)+和 22(-2)+的电离能，电离能等于能级的负值。从图1可以看出，低激发态22(-2)+的电离能随磁场增大而增大，即能级随磁场增加而减小；高激发态1320-和132(-2)+对应无磁场情况下的1s29p2P0、1s29d2D-2电子态，其电离能随磁场增加而减小，即能级随磁场增加而升高，而且当磁感应强度小于约0.02 a.u.时,激发态1320-的电离能高于132(-2)+能级，即激发态1320-的能级低于132(-2)+的能级，当磁场增加到超过0.02 a.u.时,1320-的电离能低于132(-2)+的电离能，即出现能级反转现象，表明1320-的能级高于132(-2)+的能级。

图1 Li 原子的三个原子态13 20-、13 2(-2)+ 和 2 2(-2)+的电离能随磁感应强度的变化

图2 Li原子的价电子的 2 2(-2)+态的几率密度随磁感应强度的变化，磁感应强度γ分别为0、0.000 1、0.001、0.01、0.1 和 1 a.u.

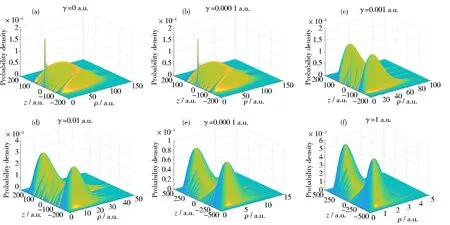
图3 Li原子的价电子的13 20-态的几率密度随磁感应强度的变化，磁感应强度γ分别为0、0.000 1、0.001、0.01、0.1 和 1 a.u.

图4 Li原子的价电子的13 2(-2)+态的几率密度随磁感应强度的变化，磁感应强度γ分别为0、0.000 1、0.001、0.01、0.1 和 1 a.u

3 结 论

本文假设原子核的质量为无穷大，忽略相对论效应，应用改进后的二维B-spline理论和计算方法，对Li原子采用模型势，建立柱坐标系，选定磁感应强度分别为0.000 1、0.001、0.01、0.1和 1 a.u.，计算了处在磁场中的Li原子激发态22(-2)+、1320-和132(-2)+的能级和几率密度空间分布。而这些磁场中的激发态分别对应无磁场中的Li原子的1s29p2P、1s29d2D和1s24d2D原子态，在磁场中发生塞曼效应后对应的是1s29p2P0、1s29d2D-2和1s24d2D-2激发态。

所提出的理论和计算方法不仅适用于求解强磁场中Li原子的基态和低激发态的能级也适用于研究高激发态的能级问题。鉴于本文首次计算Li原子在磁场中高激发态1320-和132(-2)+的能级，没有其他数据可对比，为了验证计算结果的正确性，计算了该两个态在零磁场的能级并与NIST实验数据对比，结果显示两组数据十分吻合。零场的低激发态1s24d2D-2在有磁场时记为22(-2)+，其能级随磁场增加而降低；高激发态1320-和132(-2)+的能级随磁场增加而升高，而且在磁场强度很小时，1320-的能级低于132(-2)+能级，当磁场增加到超过0.02 a.u.时出现能级反转，激发态1320-的能级高于132(-2)+的能级。对于低激发态22(-2)+在磁感应强度很小时对几率密度影响不大，当磁感应强度大到一定程度，即本文选定的磁感应强度为0.01 a.u.时开始延ρ和z方向都有一定的压缩；对于高激发态1320-及132(-2)+的几率密度分布随磁感应强度的增加改变十分明显，几率密度分布在ρ方向得到压缩，z方向被扩张，几率密度分布延ρ方向向着z轴被压扁。这种变化主要由于随着磁感应强度的增加库仑力和抗磁性都起主要作用，从而引起了几率密度分布明显改变。本文的研究结果可为复杂原子在强磁场中的动力学研究提供一定的理论基础，在计算方法上具有一定的指导价值。