8 MV医用电子加速器放射治疗中对患者其它器官的辐射剂量计算

于天祜， 孙普男

(黑龙江大学 物理科学与技术学院，哈尔滨 150080)

0 引 言

癌症是造成人类非自然死亡的主要因素，其中肺癌是死亡率最高的癌症。在美国造成死亡率最高的是肺癌，在2016年时占比为26.5%[1]。放射治疗是现在世界上对于癌症的主要治疗手段，但是在治疗癌症的同时,由于散射同样会导致其他器官受到一定剂量的辐射。由于各个器官的承受能力有所不同，计算人体内在加速器工作期间的散射十分重要。近年来,国内外对肺癌不同的放疗剂量、照射方式对病人的康复情况做出了许多跟踪研究[2-4]，给出了肺癌放射治疗参数对人体的医学影响。文献[5]给出了水下不同深度的照射剂量相对强度的实验测量值。目前，还没有关于医用电子加速器放射治疗中对患者其它器官的辐射剂量计算和实际测量值。

本文采用微元法，通过蒙特卡洛模拟和理论计算，给出了一个肺癌放射治疗期内对其他器官所受到的散射剂量值，并分析对人体可能造成的影响。为了验证本方法，计算了水下不同深度的照射剂量相对强度的理论值，与文献[5]中实验测量值进行了对比，两者相符。

1 对象和方法

1.1 加速器参数

计算加速器的型号为DZ-12/4多能量档电子直线加速器，其参数为：能量在6～12 MV之间可调[6]；焦点剂量率可达4 Gy·min-1；视野范围在5 cm×5 cm到20 cm×20 cm之间可调，标称功率为4 kW，脉冲重复频率为50～350 Hz，机器泄露率为0.1%。

1.2 肺癌的治疗过程

放射治疗是治疗肺癌的主要手段，在国内一般情况下的放射治疗过程中正常成人共计需要照射60 Gy的剂量来确保杀死肺癌细胞[7]，这些剂量通常进行分割在6周完成，每周照射量为10 Gy,共分为5次，每次照射量为2 Gy，每次照射时间1 min。放疗时所需要开的照射野的大小在5 cm×5 cm到20 cm×20 cm内。在放射治疗过程中，根据不同人体质的差别可以更改计划，如遇严重病症时，可考虑加大剂量、缩短时间。

1.3 计算模型

在放射治疗时可将照射过程近似如图1所示的模型。图1为接受放射治疗时的人体平躺时的侧面图，其中以水体为模型模拟人体的尺寸为100 cm×80 cm×50 cm，d为放射源到人体表面的距离，d1为人体表面到治疗靶器官肺的距离100 cm，d2为受散射影响的参考器官距离靶器官的距离。本文中所采用的蒙特卡洛模拟就是使用此模型编程，计算时所选用放射源处为中心点，d方向为x轴正方向，由肺部往脚方向为y轴正方向，肺部向两侧手臂方向为z轴正方向，放射治疗时视野大小为10 cm×10 cm，照射野中心点位于人体表面，坐标为(100，0，0)。放射源距离人体100 cm，人体内肺部距离人体表面13 cm。人体内肺部中心距离人体表面13 cm，肺部大小为15 cm×15 cm×15 cm，照射野中心点水平距模型头部边缘25 cm，距模型两侧手臂40 cm。

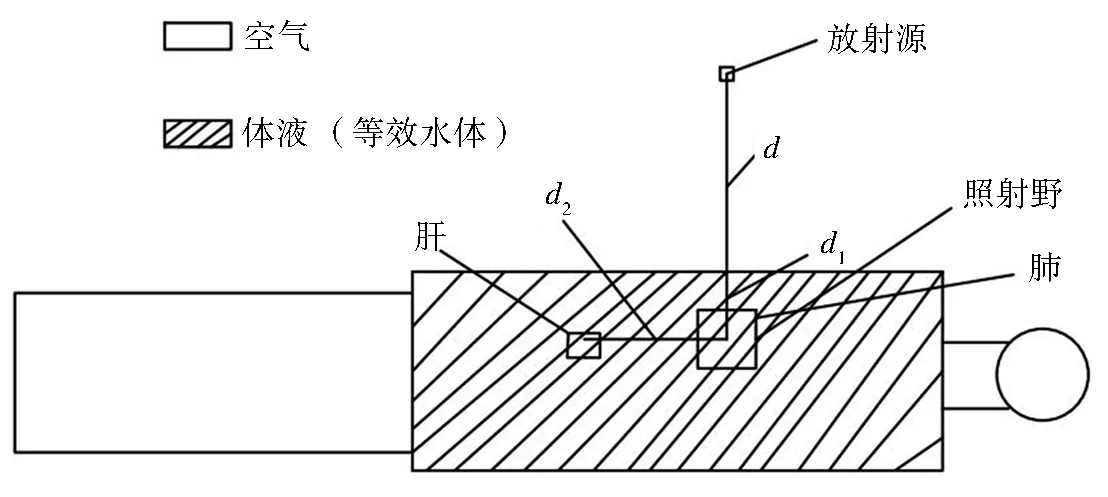
图1 放射治疗肺癌的简化模型

2 理论计算及蒙特卡洛模拟结果

2.1 理论计算

2.1.1 空气中X-、γ-射线的比释动能率常数的计算

在很多参考文献中，X-、γ-射线的空气比释动能率常数给出的都是分立值[8]，对应最大的 X-、γ-射线的能量为60Co的1.25 MV，而本研究涉及的X-射线能量为8 MV。因此，通过蒙特卡洛模拟计算X-、γ-射线能量以0.1 MV为单位，在0.1～8 MV的 X-、γ-射线在空气中的比释动能率常数Γk，单位为mGy·m2/h·GBq。其与比释动能率的关系满足：

(1)

式中：A为放射源的放射性活度，GBq；r0为人体表面在空气中距放射源的距离，m。

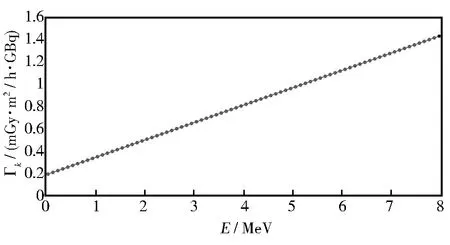
图2 能量与比释动能率常数之间的关系

蒙特卡洛模拟出比释动能率常数Γk(mGy·m2/h·GBq)和X-、γ-射线能量E(MV)的关系满足拟合公式：

Γk=0.156 7E+0.185

(2)

根据拟合式代入能量值就可以求得比释动能率常数。

2.1.2 蒙特卡洛模拟计算方法

由于X-射线的能量分布是一个连续谱[9]，并不是单一的能量值，所以在模拟计算的时候无法输入连续的能量值。计算中，首先根据Geant 4程序模拟计算得到的8 MV能量的X-射线能谱图3，通过微元法[10]，以0.1 MV为单位将0～8 MV的能量分为80份，其中峰值能量的光子强度为A，其他每份能量与峰值能量光子强度之比为ki(i=1，2，3…,80)。即其余能量分别具有的光子强度为kiA，物理意义为在能量差为0.1 MV区间内的每份微元所占的光子强度。通过同样的方法可以通过积分计算出能量为8 MV的X-射线所具有的峰值光子强度A的理论值，由于放射治疗期间要求满足：

图3 8 MV医用电子加速器的能谱图

(3)

式中：ki为第i个微元的光子强度与峰值光子强度的比值；Γki为该微元能量所对应的X-射线的照射量率常数，可以根据式(2)得出。

8 MV加速器对应的峰值活度A=2.985 1×106Bq。

2.2 微元法的蒙特卡洛模拟与实验测量结果的对比

为了证明用微元法计算剂量率正确性，本文模拟计算了文献[5]条件下，水下不同深度的照射剂量相对强度的计算值。条件为：常温常压下、X-射线焦点剂量率2 Gy·min-1、照射源距水面照射野中心点距离100 cm、照射野为10 cm×10 cm、水箱体积为100 cm×80 cm×50 cm。在给定水下深度后，分别输入80个微分元的光子能量和强度，用蒙特卡洛模拟方法计算每个微分元的照射剂量，把80个微分元的照射剂量求和，得到该水下深度的照射剂量。计算0～21 cm水下不同深度的照射剂量，间隔为0.5 cm。找出最大剂量点深度，其他水下不同深度的照射量与该点的照射量相比，就可得出水下不同深度的照射剂量相对强度的计算值。两者数据基本相符如表1所示，证明了微元法的可行性。可以看出，此方法的计算结果与实际测量值较为相符，表明微元法可应用于人体内散射剂量值的计算。

表1 10 cm×10 cm野下深度与百分深度剂量之间的关系

2.3 散射计算的蒙特卡洛模拟

通过所建立的计算放射治疗中的人体基本模型，进行蒙特卡洛模拟编程。计算中,用水体来模拟人体，使用F8卡得出剂量当量率值。在对散射光子进行模拟计算过程中，光子和电子的截断能量为 8.3 MV，计算总事件数量为 5亿。蒙特卡洛计算所采用的粒子输运程序为 Geant 4程序,版本为 4.9.0。由于X-射线的输出为连续谱，本文也同样在计算时通过将区间划分成80个点的微元法进行计算。得到的蒙特卡洛模拟计算的结果普遍大于理论值，这是由于蒙特卡洛计算时考虑了轫致辐射等一些其他的散射现象[11]。

一台放射治疗期间总照射剂量为60 Gy的仪器，放射治疗时分为6周照射，单次照射剂量为2 Gy，共计30次，单次照射时间为1 min。取参考点为水平距离肺部不同距离的器官，开照射野大小选为10 cm×10 cm。放射源垂直距离人体表面100 cm，在人体内的相对剂量百分比的大小如图3所示。8 MV能量的医用电子加速器放射治疗所引起的人体内产生的散射随距离变化引起剂量当量值如表2所示。

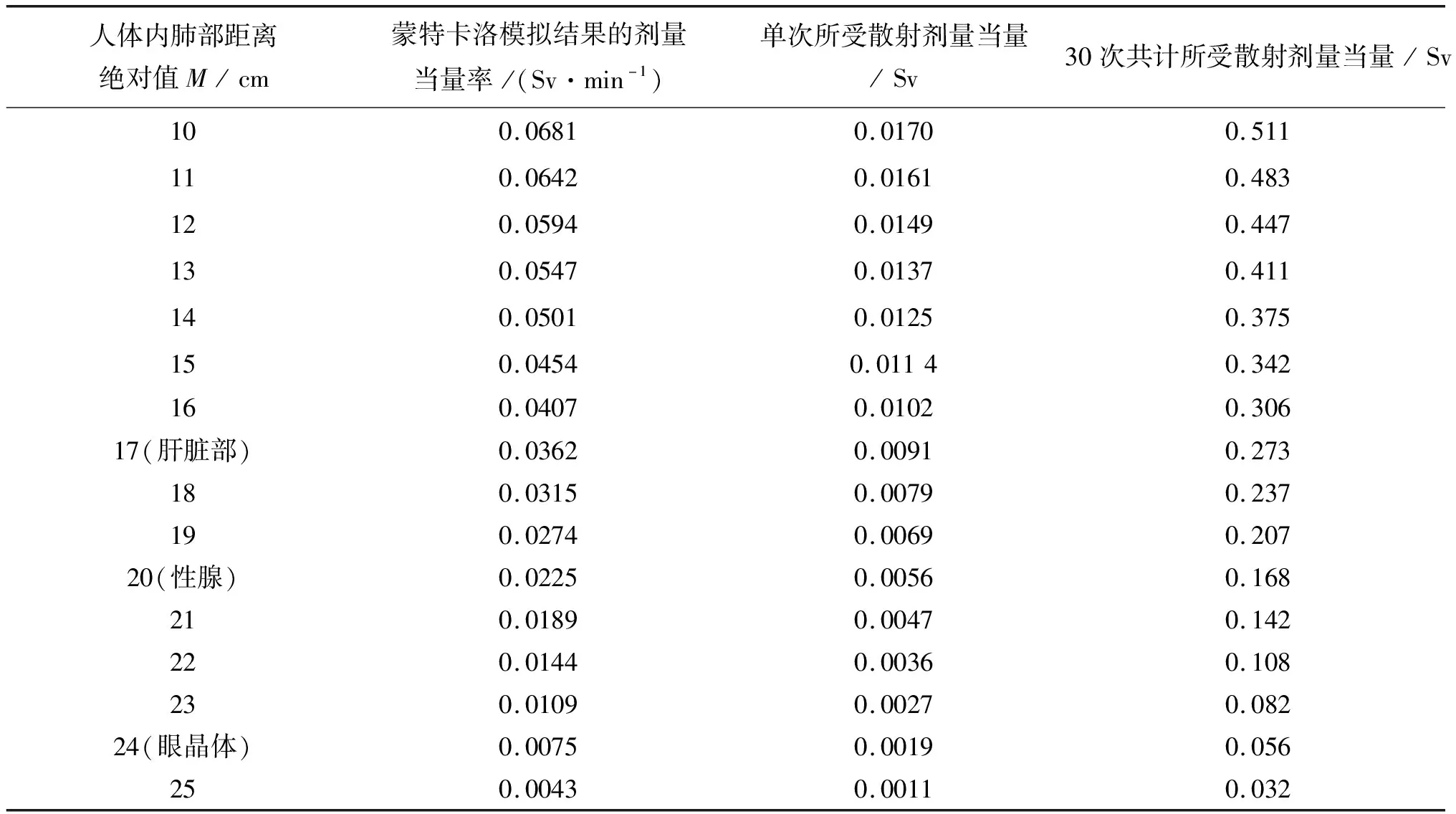
表2 人体内距肺部治疗区中心距离与散射剂量当量之间的关系

图3 10 cm×10 cm野百分深度剂量分布曲线

对于计算散射时的剂量率，大小等于将能量分为以0.1 MV为单位的各个微元所产生的剂量率之和。数据模拟成预测曲线如图4所示。

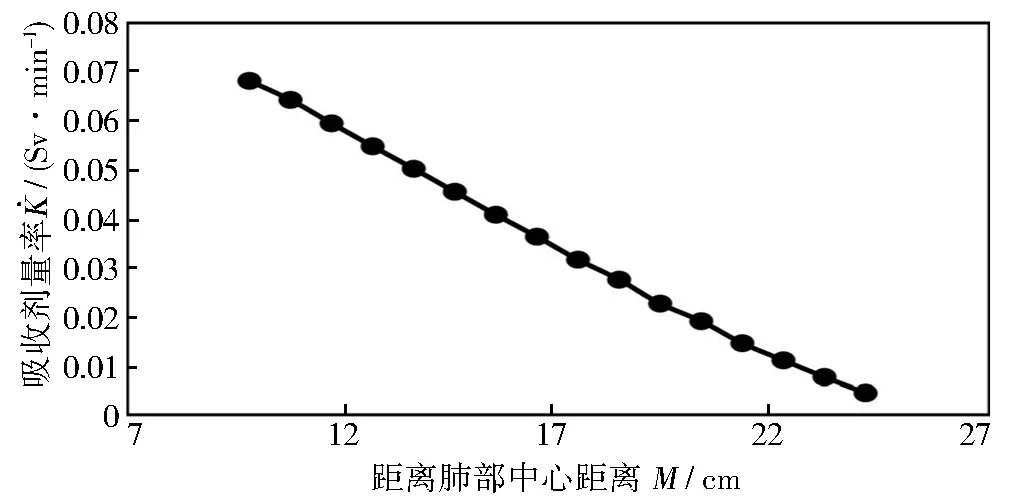
图4 人体内照射处距离与散射吸收剂量关系曲线

3 放射治疗中受到的总辐射及对人体的影响

在国际辐射防护委员会(International Commission on Radiological Protection, ICRP)于1977年提出使用确定性效应和非确定性效应来对X-射线对人体的生物效应进行了区别。按照ICRP第103号出版物所给出的结果，对于成人人体所受剂量每增加0.01 Sv会引起确定性效应即直接患癌率会增加0.41‰，不确定性效应即遗传效应会增加0.01‰[12]，高剂量率比低剂量率的损伤效应更加明显，这是因为高剂量率的照射使机体对损伤的修复作用不能充分表现出来所致。如在本文所考虑的性腺部位所受到的单次剂量当量为0.005 6 Sv，30次总共所受到的剂量当量为0.168 Sv，根据国家标准，其中人体所受散射剂量当量为0.10～0.5 Sv时对人体的损伤程度估计为可恢复的机能变化以及可能有血液学的变化。在确定性效应方面，对于成年人睾丸，当短暂照射剂量在3.5～6.0 Sv时才会导致永久不育[13]。可以看出,肺癌放射治疗时的散射剂量在其他器官上的影响较直接照射的靶器官普遍较低。本计算结果经过换算后得到，在肺癌放射治疗中引起肝脏、性腺和眼晶体器官直接致癌的风险分别为1.12%、0.69%和0.23%，所导致的遗传性效应分别为0.27‰、0.17‰和0.06‰，其中正常所受的天然辐射本地可忽略不计，为正常公众吸收剂量。

4 结 论

放射治疗中不仅目标靶器官所受的辐射剂量需要考虑，在人体内散射到其他器官处的剂量同样需要关注。如果同时或在一年的间隔时间内对同一人的两个器官进行治疗，其照射时所产生的散射则会导致其他器官所承受的辐射剂量率超标。在对肺癌放射治疗进行分割时，对人体内其他器官的辐射影响是根据不同器官对辐射的敏感度以及恢复力决定的，合理的安排时间间隔以及对于剂量的控制为现在肺癌治疗中的研究特点。本文中所用的变量和公式均是由其他公式推导而来，使用蒙特卡洛模拟验证，具有一定的参考意义，该评价以及研究问题的方法对于相关医学治疗领域同样具有实用价值。