参数优化GBDT算法的密封继电器材质识别

吕冰泽, 王国涛,2, 汪国强, 李 硕

(1.黑龙江大学 电子工程学院, 哈尔滨 150080；2.哈尔滨工业大学 电器与电子可靠性研究所, 哈尔滨 150001)

0 引 言

密封继电器作为一种常用的航天元器件，在航天设备中起着重要的作用。因此，密封继电器的可靠性会直接影响到航天设备的可靠性[1]。在诸多问题中对密封继电器可靠性影响最大的就是内部多余物问题。继电器在制作中容易将不易发现的铝粒、焊锡和热熔胶等多余物微粒混入密封腔体内部，当设备处于失重或者超重的环境下，会对腔体内部的多余物微粒产生激励，使其产生无规则运动，微粒可能移动至组件连接处或触点间[2]。当金属多余物处于电路触点时易产生电弧破坏内部结构，而非金属多余物卡在组件连接处会使得继电器无法正常运行导致系统失效[3]。

美国是最早关注多余物问题和研究微粒碰撞检测法的国家，国内对于多余物的材质识别的研究主要集中于哈尔滨工业大学[4]。文献[2]首次提出基于时域和频域特征，实现了对金属和非金属多余物材质特征识别。文献[5]提出基于学习矢量量化网络(Learning vector quantization, LVQ)和特征级数据融合的多余物材质识别方法，对继电器中锡粒、铜丝、橡胶和导线皮多余物进行了材质识别，但是其研究的材质识别分类器参数依靠经验确定，材质识别模型复杂且泛化能力较差，最终并未应用于实际。文献[6]提出了基于改进型梅尔频率倒谱系数(Mel frequency cepstral coefficients, MFCC)的多余物材质特征识别方法，建立了多余物材质概率统计模型，选用多余物材质敏感频域特征，实现了对导线皮、芯片、铝和锡粒的有效识别。依据Mel滤波器设计原理和多余物信号的频谱特征，设计了一种基于敏感频域的Mel滤波器，提出适用于多余物信号的改进型MFCC特征提取方法，提升了多余物信号的有用信息，但是该方法缺乏实现设备，并没有与多余物检测设备结合起来，仍然未应用于实际。

综上所述，由于目前在对多余物信号进行研究时一般使用传统信号分析方法或者采用如KNN和支持向量机等经典的机器学习算法[7-8]，尽管可以对多余物材质进行识别分类，但准确率还有待提高。所以，本文提出一种采用参数优化的梯度GBDT算法对密封继电器中的多余物进行金属和非金属微粒材质分类。并且在原有特征的基础上，采用小波变换的方法提取了多余物信号能量特征。为了提高金属和非金属材质识别精度，加快模型训练过程中参数优化的效率，引入了Python中的分布式异步超参数优化模块Hyperopt，使用树形评估器Parzen对基于默认参数的GBDT算法进行参数调优。实验表明，基于贝叶斯优化的GBDT分类算法可以有效提高密封继电器多余物材质识别的准确率。

1 多余物特征提取

1.1 传统特征提取

受实验环境等因素的影响，在进行颗粒碰撞噪声检测(Particle impact noise detection，PIND)实验时，会采集到一部分噪声信号随机分布在多余物信号中，需要先去除数据中的噪声[9]。常见的多余物信号特征一般从频域和时域两个部分进行提取，在频域上目前采用短时傅里叶算法来进行多余物特征提取。主要将信号通过窗函数处理使其由不平稳信号加以平稳，再经过傅里叶变换得到局部的频谱特征值。在时域上，可以直观地表现出信号的根本特征，本文选取了脉冲面积、脉冲左右对称度、脉冲上下对称度、脉冲持续时间、脉冲上升占比、能量密度、脉冲占比、波峰系数、面积占比、频谱质心、均方频率、方差、过零点率和均方根差14个特征。

1.2 小波变换特征提取

1.2.1 小波变换

由于短时傅里叶变换需要对窗函数进行设置，但是在实际应用中需要对窗函数的长度只能设置常见值或者进行多次尝试，当长度较短时，会导致截取的局部频率不够精准；当长度过长时，会出现范围过广不能对实时变化情况作出描述的情况，所以需要一种新的方法能精确地将信号的频谱特征加以表达。小波变换的选择就是能对这个问题进行解决，小波变换通过对原始信号进行层级分解，在不同的层级根据所分解的信号进行适当的窗函数调整，这样能够对信号的频谱信息更好地进行表达[10]。本文在原信号的基础上，采用小波变换对新的特征加以提取。

在小波分析中，可以任意选择小波基函数。本文对采集信号低频部分连续进行3层分解，得到关于原始信号小波变换的能量特征，小波变换是一种具有低时间分辨率和高频谱分辨率的快速算法[11]。

1.2.2 能量特征提取

小波变换主要通过小波函数来分析非平稳信号，在材质识别中，提取金属和非金属微粒所包含的隐藏特征。因此，通过数值分析，计算出小波变换系数的能量值。

一维信号X(t)的小波分解[10]为：

X(t)=Gj+∑Zj

(1)

式中：G为低频分量的近似信号；Z为高频分量的细节信号。

一维信号X(t)与尺度函数V通过卷积运算可得到低频的近似系数cGj(t)。一维信号X(t)与小波函数通过卷积运算可得到高频的细节系数cGDj(l)。其近似系数和细节系数为：

(2)

小波能量系数为：

(3)

式中l= 1,2,…,N/2j-1，N是信号长度。

选择第3层近似系数的能量和各层细节系数的能量作为信号特征，然后构建小波能量系数特征向量模型为：

[EGj,EZ1,EZ2,···,EZj]

(4)

选择小波系数中的双正交(Biorthogona)小波，分别对金属和非金属微粒进行小波3层分解，使用式(2)分别得到1个小波近似系数和3个细节系数，使用式(3)提取近似系数的能量和各层系数的能量，作为多余物微粒特征。

2 算法原理

2.1 GBDT算法

梯度增强决策树(GBDT)是在增强算法(Boosting)的基础上，采用梯度增强算法通过依次迭代生成决策树，高效地解决二分类问题的方法。梯度提升的训练目的是为了减少与上一次训练之间的残差，通过不断地在梯度方向上训练新的模型，通过逐渐降低残差逼近目标函数，最后达到误差最小化[11-12]。在GBDT的训练中，假设上一轮的迭代得到了强学习器是fm-1(X)，损失函数是L(fm-1(X))，本轮的目标是通过训练学习找到一个弱学习器hm(X)，让损失函数L(y,fm(X))=L(fm-1(X))+hm(X))最小，在这里一般定义 GBDT分类的损失函数为：

L(y,fm(Xi))=-(yilogρi+(1-yi)log(1-ρi))

(5)

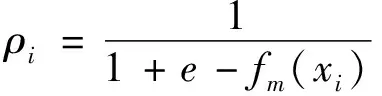
GBDT算法流程主要分为以下步骤：

步骤1：对弱学习器

(6)

进行初始化，并确定初始化函数式(7)，利用损失函数式(5)计算出最佳初始值。

(7)

步骤2：对于输入样本m=1,2,…,M，建立出M棵决策树，建立过程如下：

(a)对每个决策样本i=1,2,…,M,计算其负梯度，利用式(8)确定每一轮的残差值。

(8)

(b)将(a)中得到的残差作为训练数据，再次对其训练学习，得到新的决策树fm(X)，其对应的叶子节点区域为Rjm，j=1,2,…,J,其中J为决策树m的叶子节点个数。

(c)通过函数(9)对叶子节点j=1,2,…,J计算最佳相似度，即拟合值。

(9)

该步骤会对叶子节点的残差值进行变换，γjm表示第j个叶子节点残差转换值，yi表示第j个叶子节点上样本xi的类别概率观测值，fm-1(xi)表示第j个叶子节点的样本xi在上一棵树上的预测值，γ是常数(第j个节点的残差转换后的值)。对于每个节点都有一个最优残差转换值γjm是第j个叶子节点的观测值yi与fm-1(xi)之间的最小误差[13]。通过损失函数对γ微分即可找到每个节点的最优残差转换值。

(10)

(d)对前一轮训练得到的强学习器进行更新，得到函数为：

(11)

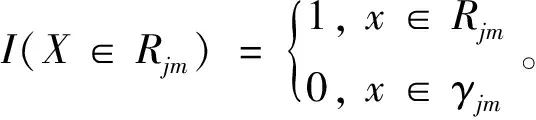
步骤3：通过不断的迭代学习，得到强学习器为：

(12)

在迭代过程中，如果损失误差小于设定的阈值，未达到给定的迭代次数，则返回式(12)继续学习。然后算出分类的概率值与设定值对比，并将结果标记为相应的所属类别。GBDT算法训练过程如图1所示，其中T表示输入数据集，F(X)表示输出梯度提升模型。

图1 GBDT算法训练过程

2.2 Hyperopt参数调优

超参数优化对机器学习算法的必要性已在许多文献的实验研究中都得到了证明。大多数的机器学习算法，如深度神经网络和梯度提升模型等都需要借助优化算法将模型性能调整至最佳。通常情况下有两种类型的参数调试方法，网格搜索(Grid search)和随机搜索(Random search)。网格搜索速度慢但是适用于需要随整个参数空间进行搜索的情况；随机搜索速度很快,但是容易遗漏一些重要信息。网格搜索调参方法在搜索空间方面效果更好，但速度较慢，而随机搜索很快，但可能会错过搜索区域中的重要信息。而Hyperopt使用贝叶斯优化的形式进行参数调整，可以自适应的为给定模型获得最佳参数，在大范围内优化具有数百个参数的模型[14]。综合考虑下，本文使用Python中的Hyperopt工具执行贝叶斯优化，从而对所建立的模型进行调参。

使用Hyperopt主要采用四个步骤：

步骤1：确定目标函数。对于所要评估的模型首先需要将其最小化，由于Hyperopt将目标函数进行“黑箱”处理，所以只是对输入和输出值进行处理，使得输出为最小化的实值，找到损失最小的输入。

步骤2：对目标模型中的超参数划分不同参数值的空间范围。对于贝叶斯优化中的每个超参数来说，空间阈值的概率密度是呈离散分布的。由于不同训练集之间的最佳模型空间范围很难确定，因此在参数优化时，采用多个阈值点来设定每个参数之间的边界值。

步骤3：构造代理模型并选择树结构估计算法(Tree-structured parzen estimator, TPE)评估超参数值。

步骤4：将评估后的损失函数和最优参数进行输出。

由于GBDT算法采用Boosting框架构成，其弱分类器为CART回归树组合而成，所以此时首先对其弱分类器进行参数调优，对回归树进行修剪，在决策树的训练学习过程中，有些节点分类是意义不大的，而这些节点的存在不仅增加复杂度，而且减少了分类器的正确率。决策树模型有很多超参数，但不是所有参数都需要调试，主要需要调试树的最大深度、最大叶子节点数和内部节点再划分所需最小样本数这几个超参数。

3 材质识别模型构建

基于GBDT算法和Hyperopt模块的原理介绍构建多余物材质分类模型，实现对多余物微粒金属和非金属的材质识别。由于GBDT算法以回归树作为基本分类器，因此，弱分类器一般选择具有偏差较大的回归树模型。在迭代训练生成决策树时，通过不断降低偏差来提高弱学习器集成的强学习器的模型精度。同时，预测模型的因变量是连续的数值型变量，因此，选择平方损失函数作为模型的损失函数。

输入:T={(x11,…,x17,y1),…,(x11,…,x17,y1)}，损失函数为：

(13)

初始化弱分类器：

对式(13)中的平方损失函数直接求导，令导数等于零，得到：

(14)

式中：c的取值为所有训练样本标签值的均值。对于m=1,2,…,M，对样本i=1,2,…,n，根据式(8)计算损失函数的负梯度值，利用数据集(xi,rmi)拟合下一轮基础模型。得到第m棵决策树的叶子节点，并计算各叶子节点的最佳拟合值。

(15)

式(15)表示cmj的取值为第m棵树的第j个结点中残差的均值。

更新式(16)，得：

(16)

得到新一轮函数值，结合前(m-1)轮的基础模型，加入学习率防止模型过拟合，得到梯度提升模型函数为：

FM(x)=FM-1(x)+vfm(x)

(17)

式中v为学习率。

为了提高识别准确率，采用默认参数建立基于GBDT多余物金属非金属分类模型后，使用Hyperopt对其进行参数优化提高模型整体效率[15]。为克服数据集自身造成的缺陷，还将采用k折交叉检验的方法。通过将整体数据集分为k份，在对模型进行训练时，将其中K-1份进行训练，然后将剩下的一份数据集作为数据集进行测试，对上述操作重分k次，每次采用不同份的数据集进行实验，最终将k次检验的结果求均值输出作为最终结果。

4 实验分析

4.1 多余物材质数据集

选择来自某型号密封继电器采集到的一组数据集来评估该材质识别模型的有效性，采集到的主要数据集信息如表1所示，其中包括了样本总数，金属微粒数量和非金属微粒数量，以及数据集选择的特征总数。

表1 数据集的主要信息

为了识别试验效果，对处理后的数据集采用参数优化的GBDT算法进行分类验证。在进行实验时，70%的数据用于训练GBDT模型；30%的数据用来预测分类模型，评估模型的识别效果。

通常情况下，信号的特征信息越丰富，对于模型识别精度提高就越明显。在原有脉冲面积、脉冲左右对称度、脉冲上下对称度、脉冲持续时间、脉冲上升占比、能量密度、脉冲占比、波峰系数、面积占比、频谱质心、均方频率、方差、过零点率和均方根差14个特征的基础上，对原始信号进行小波变换得到信号频带分析，将计算得到的每个频带能量作为新特征。与本文原有特征相结合组成新的样本数据集进行了分析，提取出的部分特征如表2所示。

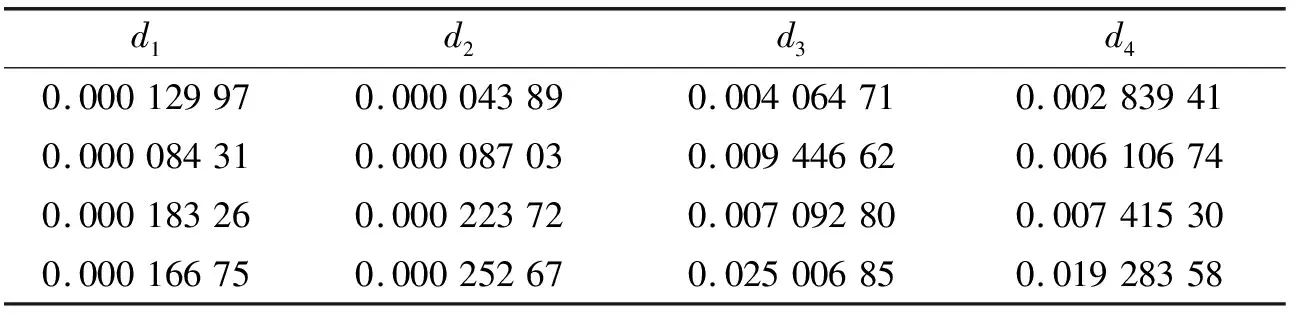
表2 小波变换部分特征集

4.2 评价指标

对于机器学习分类算法，存在样本过拟合问题。为了更好地对模型性能加以反映，在保证了准确率不变的基础上使用混淆矩阵评估模型调参的效果，如表3所示。

表3 二分类混淆矩阵

在对该模型进行评估时，经过各个评价指标对比，最后选择查准率(Precison)、召回率(Recall)和F1-score三个值作为评价指标。

“查准率”是用来表示预测集中被预测正确的个数，定义为：

(18)

召回率主要是查找有多少样本能被找回公式为：

(19)

F1-score是综合评价查准率和查全率的评价指标，为查准率和查全率的调和平均数[14]。计算方法为：

(20)

式中，β=1时，F1-score值一般情况下β=1。F1-score值能很好地反映二分类的分类效果。

4.3 实验验证

为了验证加入小波变换能量特征后的整体特征集的识别效果，使用原有特征组合进行机器学习模型识别,结果如表4所示。

表4 原特征集测试结果

此时，模型的精确度为0.90，使用加入小波变换后的特征集采用同样的模型进行金属和非金属识别，得到的测试结果如表5所示。

表5 新特征集测试结果

加入新特征后模型精确度为0.914，准确率提高1.4%。此外，由表4和表5中的判别指标对比可以发现,对非金属的检测效果有所提升，证明加入小波变换的能量特征可以提高多余物材质分类精度。

本实验采用GBDT算法进行密封继电器中金属和非金属多余物材质识别，由于GBDT算法是基于Boosting框架下的集成算法，由弱分类器回归树(CART)组成，主要选择贝叶斯优化法对弱分类器中的最大深度(max_depth)和最大特征数(max_features)进行单棵树的优化。在Boosting框架下，n_estimators表示整个模型弱分类个数，在实际参数优化过程中，一般与learning_rate，即每个弱分类器的权重缩减系数共同进行调优。

在训练集上将learning_rate设置为0.5，并采用5重交叉验证对参数n_estimators进行寻优，结果为800。再用同样的方法对max_depth和max_features进行超参数的选择，参数值均为5。

在进行参数选择后，基于前面的模型构建，利用数据集分别在优化前后的GBDT模型上进行测试。此外，为了分析GBDT模型的分类效果，分别以KNN分类模型和SVM支持向量机模型测试结果进行对比。采用默认参数进行测试得到准确率为0.902，采用Hyperopt对其进行参数优化，得到整体模型参数优化数值，如表6所示。

表6 模型参数优化

参数优化后与优化前模型对比测试结果如表7所示。

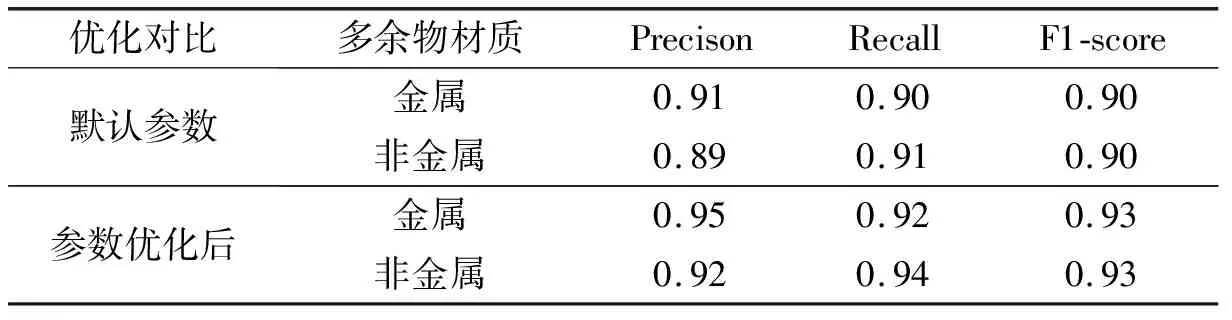
表7 默认参数测试结果

经过参数优化后，模型整体准确率可以达到93.2%，比默认参数模型准确率提升了3.1%，此外，其他评估指标也有一定的提高。将优化后的模型与目前常用的KNN分类模型和SVM支持向量机模型进行对比，分类准确率对比如表8所示。

表8 不同模型的分类准确率

由预测结果可以看出，参数优化后的GBDT算法的分类准确率更高，准确率为0.932。分类结果优于KNN、支持向量机模型和基于默认参数的GBDT分类模型。因此，参数优化后的GBDT模型为分类结果最佳的选择。由表9可以看出，与默认参数的GBDT算法相比，使用参数优化的GBDT算法对金属和非金属微粒识别时，各项指标都有提升，这相比传统的检测方法的精确度也有一定程度的提升，尤其对非金属识别的准确度提升较高。虽然使用SVM支持向量机算法的二分类各项指标也能很好地反映金属微粒和非金属微粒分类效果，但由于泛化性较低，因此，使用参数优化的GBDT算法能够有效地提升金属微粒和非金属微粒的准确度。

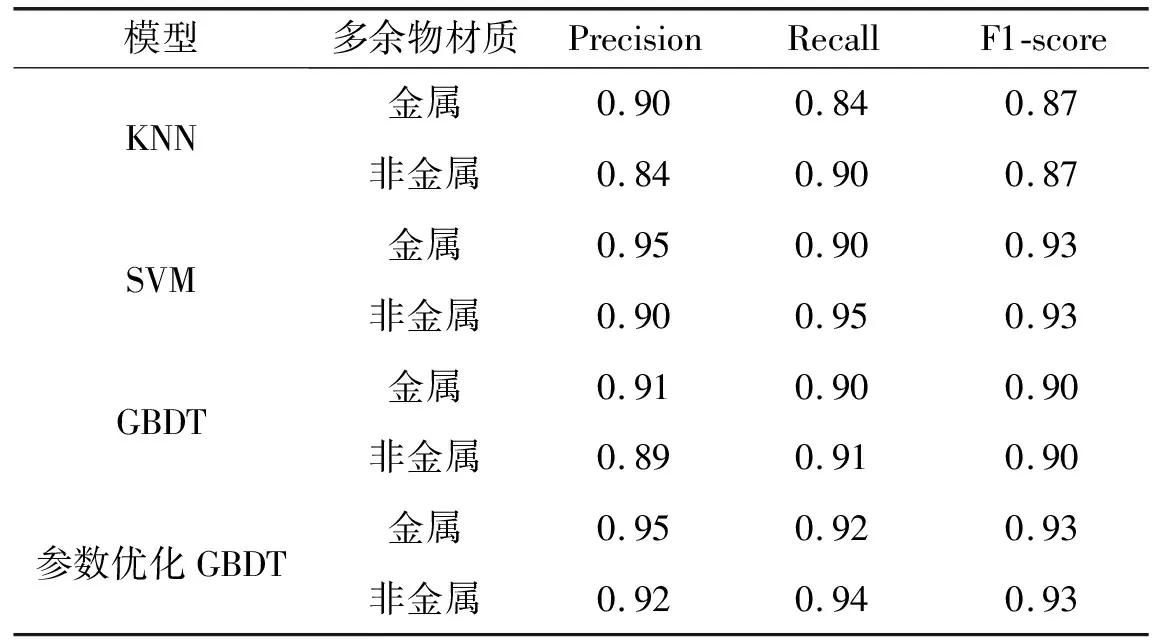
表9 评估指标值

5 结 论

采用贝叶斯参数优化的GBDT算法对航天密封继电器内部的金属和非金属微粒进行材质识别。在原有特征的基础上，利用小波变换提取了能量系数作为特征值。实验验证，加入新特征后模型识别准确率提升了1.4%。根据GBDT算法流程建立了材质识别的分类器模型，并使用Hyperopt模块的TPE评估器对多余物微粒识别模型进行超参数调优。实验结果表明，调参后的GBDT算法具有更好的分类效果，分类准确率提升到93%，提升了3.1%。同时，3个评价指标相对于KNN分类模型和SVM支持向量机模型也有一定的提升，其中精确度、召回率和F1-score值均提升超过了3%。此方案可以提高密封继电器金属和非金属微粒的识别准确率。通过对多余物的材质信息更准确的识别，还可以改善多余物的生产环节，进一步推动相关材质的改进，提高整个航天系统的可靠性。