一类指数型非线性随机差分方程组解的稳定性分析

佘智凤, 廖新元, 陈沙沙, 金 薇

(南华大学 数理学院, 湖南 衡阳 421001)

0 引 言

众所周知，大自然中事物的发展都有其客观规律，最开始，人们用确定性模型来刻画系统。实际上，世界的本质是随机的，这些系统受到自然界多种因素的影响，有些影响比较大，不可忽略，1953年，杜布出版了名著《随机过程论》，系统地叙述了随机过程基本理论。

随机差分方程由于考虑了现实世界多种因素对系统的影响，较之确定性方程，能更准确地描述实际生活中的现象和实物发展的客观规律，这促使国内外学者纷纷投入研究，并取得了丰富的研究成果，此后随机差分方程的研究工作迅速发展。随机差分方程在经济学、生物学、地质学和物理学等各个领域中都有广泛的应用[1-9]。

对有些问题的研究，线性随机差分方程不能准确地描述实际动力学性态，具有一定的局限性，为了便于研究，许多学者建立了指数型差分方程[10-16]。但忽略了自然界中各种随机扰动的存在，相较而言，指数型非线性随机差分方程更贴切于现实情况。例如，文献[17]中，L.Shaikhet在指数型离散时滞蚊子种群方程的基础上，考虑了随机扰动对系统的影响，研究了指数型随机蚊子种群方程在平衡点处依概率稳定的充分条件。本文在其基础上，考虑了双随机扰动，研究其类似的方程组系统平衡解稳定的充分条件。

1 正平衡点

本文考虑下列指数型非线性随机差分方程组系统平衡解稳定的充分条件

n=0,1,2，……,x1(j)=φ1(j),

x2(j)=φ2(j),j=-1,0。

(1)

Eξk(n)=0,E2ξk(n)=0,Eξi(n)Eξj(n)=0,

i,j=1,2,3,4,i≠j。

首先求解模型正平衡点存在的参数条件及正平衡点满足的条件。

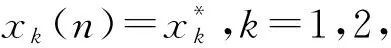
(2)

显然，对任意的正参数，即a,b,c,μ,v>0，方程(1)都有零解E0=(0,0)。

(3)

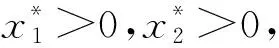
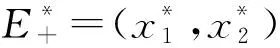
(4)

(5)

(6)

证明 1) 由方程组(2)可得

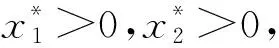
则

即η>1。

2)显而易见，条件(4)直接由方程组(2)得到。

3)将式(4)中第2个式子代入方程组(2)第2个式子得到(5)第1个式子,将(4)中第1个式子代入(2)第1个式子得到(5)第2个式子。

4)由式(4)2个式子分别可得

即

条件(6)得证。

2 线性化和一些引理

(7)

(8)

对于零平衡点E0,方程(7),(8)分别可写成

(9)

(10)

为了研究方程在零平衡点处的稳定性，先给出下列引理。

记σ-代数Fi的条件期望为Ei=E{./φi}，令Uε=x:|x|≤ε,ΔVi=Vi+1-Vi。

引理2[21]对方程(7)(或(9))，假设存在一个非负函数Vi=V(i,z(-1),……,z(i))满足下列条件

V(i,y(-1),……,y(i))≥c0|y(i)|2,

(11)

V(0,φ(-1),……,φ(0))≤c1‖φ‖2,

(12)

EiΔVi≤0,xj∈Uε,-h≤j≤i,i∈Z。

(13)

其中ε>0,c0>0,c1>0，则方程(7)(或(9))的平凡解是依概率稳定的。

引理3[21]对方程(8)(或(10))，假设存在一个非负函数Vi=V(i,z(-1),……,z(i))满足条件(12)且

EiΔVi≤-c2E|z(i)|2,i∈Z。

(14)

其中c2>0，那么方程(8)(或(10))的零解是渐近均方稳定的。

备注1：对于一个高阶非线性差分方程组，若其线性化方程存在一个泛函Vi满足条件(11)、(12)和(14)，那么其初始非线性方程组也存在一个泛函Vi满足条件(11)、(12)和(13)。为了得到非线性方程(7)(或(9))零解依概率稳定的充分条件，只需要通过构造满足条件(11)、(12)和(14)的泛函Vi以得到其线性化方程(8)(或(10))零解渐近均方稳定的充分条件。

3 稳定性条件

下面引进一个二维线性随机差分方程组

(15)

显然，方程(15)是方程(7)和(9)的更一般化的形式，则方程(15)零解渐近均方稳定的的充分条件也适用于方程(7)和(9)，为了得到方程(15)零解渐近均方稳定的充分条件，令

Q,D,U是对称矩阵，若对于两个对称矩阵Q,D，Q-D是一个正定矩阵，则记Q>D。

定理1设对于某些正定矩阵Q,矩阵方程A′DA-D=-U有半正定解D，使得

那么方程(15)的零解是渐近均方稳定的。

证明 记

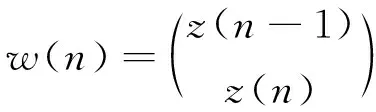
那么式(15)可以写成

w(n+1)=[A+B(ξ(n+1))]w(n)

构造Lyapunov函数V(n)=w′(n)Dw(n),则

EΔV(n)=E(w′(n+1)Dw(n+1)-

w′(n)Dw(n))=Ew′(n)([A+

B′(ξ(n+1))]D[A+B(ξ(n+1))]-

D)w(n)=Ew′(n)[A′DA-D+

B′(ξ(n+1))DB(ξ(n+1))]w(n)=

Ew′(n)[-U+B′(ξ(n+1))DB(ξ(n+

1))]w(n)=ETr(w(n)w′(n))[-U+

B′(ξ(n+1))DB(ξ(n+1))]=

TrE(w(n)w′(n))[-U+B′(ξ(n+

1))DB(ξ(n+1))]=Tr(E(z(n)×

z′(n))[-Q+Eθ′(ξ(n+1))×

D22θ(ξ(n+1))])=Tr(E(z(n)×

z′(n))[-Q+Eθ′(ξ(n+1))×

D22θ(ξ(n+1))])=Tr(E(z(n)×

z′(n))[-Q+Eθ′(ξ(n+1))×

D22θ(ξ(n+1))])=Tr(E(z(n)×

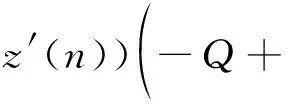
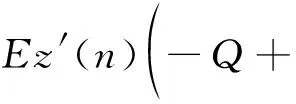
综上，EΔV(n)≤-cE|z(n)|2,由引理3可得，方程(15)的零解是渐近均方稳定的。

备注2：对方程(10)(或(8))，如果定理1的条件成立，则方程(10)(或(8))的零解是渐近均方稳定的，由备注1,可以得到，方程(9)(或(7)的零解是依概率稳定的，因此方程(1)的平衡点依概率稳定的充分条件得证。

4 数值模拟

1)令a=0.6,b=0.15,c=0.45,d=0.2,μ=ν=0.25,此时η<1，则方程(1)只有零解E0，当

由矩阵方程A′DA-D=-U，得

由引理2,引理3和定理1可得：

1)方程(10)的零解是渐近均方稳定的；

2)方程(9)的零解是依概率稳定的。

考虑方程(9),即考虑方程(1)解的轨迹。令σ11=0.11,σ12=0.25,σ21=0.31,σ22=0.11,y1(-1)=0.5,y1(0)=0.4,y2(-1)=0.6,y2(0)=0.8。如图1所示，根据方程(9)的零平衡点的依概率稳定性，其100个解的轨迹都趋向于零。

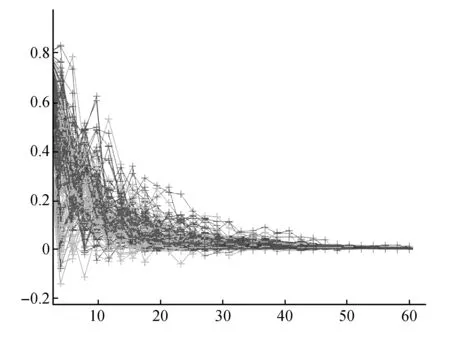
图1 方程(9)解的100个轨迹Fig.1 100 trajectories of the solution of the system(9)

2)令a=0.9,b=0.15,c=0.7,d=0.45,μ=ν=0.25,则η=2.25>1，方程(1)不仅有零平衡点E0还有正平衡点E+=(0.287,0.334)，考虑方程(1)的正解，当

由矩阵方程A′DA-D=-U，得

由引理2,引理3和定理1可得：

1)方程(8)的零解是渐近均方稳定的；

2)方程(7)的零解(方程(1)正平衡点)是依概率稳定的。

考虑方程(9)也就是考虑方程(1)解的轨迹。令σ11=0.15,σ12=0.21,σ21=0.11,σ22=0.25,y1(-1)=0.5,y1(0)=0.4,y2(-1)=0.6,y2(0)=0.8根据方程(9)的零平衡点的不稳定性，其解的轨迹如图2所示。

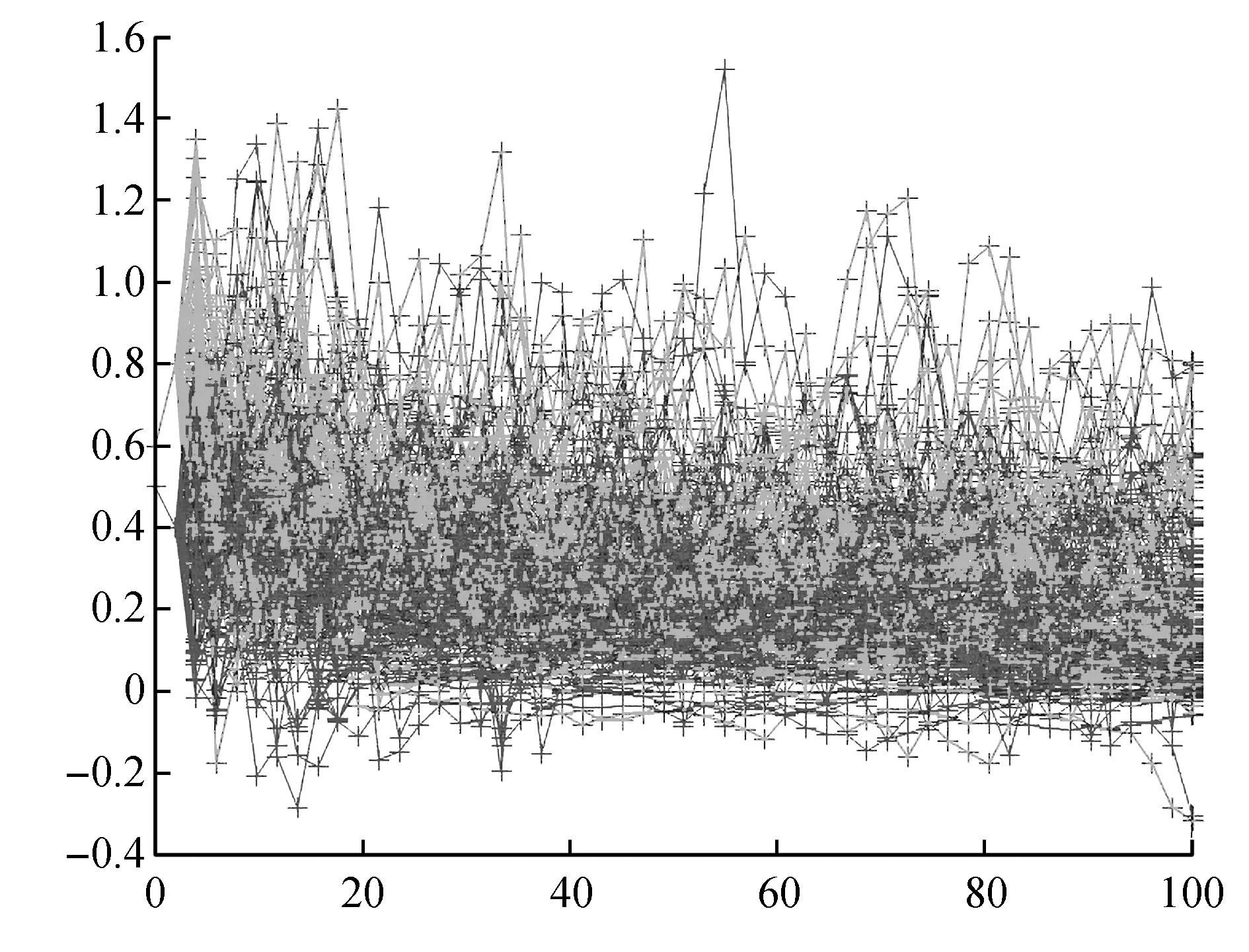
图2 方程(9)解的100个轨迹Fig.2 100 trajectories of the solution of the system(9)

考虑方程(1)的零解，当

由矩阵方程A′DA-D=-U，可得d11=0.097,d22=-0.127,d33=-5.645,d44=0.481,则矩阵D不是一个正定矩阵，方程(1)的零解是不稳定的。

考虑方程(1)解的轨迹，设方程(1)的初值函数为x1(-1)=0.5,x1(0)=0.6,x2(-1)=0.4,x2(0)=0.8,σ11=0.11,σ12=0.15,σ21=0.13,σ22=0.11,方程(1)的正平衡点是依概率稳定的，如图3所示，方程(1)的解的轨迹都收敛于正平衡点E+=(0.287,0.334)。

图3 方程(1)解的100个轨迹Fig.3 100 trajectories of the solution of the system(1)

5 结 论