多智能体系统对移动放射性辐射源的环绕跟踪

唐俊杰,刘宏亮,欧阳自根,彭宇睿

(南华大学 数理学院,湖南 衡阳 421001)

0 引 言

近年来,随着核能的利用效率不断提高,应用的范围不断增加,因放射性物质泄露或意外丢失而引发的事故也逐渐增长[1]。放射性物质所产生的辐射可对人体造成伤害,并易引发白血病、癌症等疾病[2-3]。因此,当事故发生时,最重要便是对泄漏或遗失的放射性物质进行搜寻并实时监测,防止进一步扩散。而目前在放射性物质的搜寻监测方面,主要的办法仍为人工搜寻监测,即采用专业的搜寻人员持检测设备对可疑区域进行拉网式搜索,这种办法不仅效率较低,尤其易对搜寻人员造成伤害。因此,需采取一种安全、高效的方法对泄漏或丢失的放射性物质进行搜寻监测。

目前已有许多学者已做出一些非常有建设性的工作,如Z.Liu等人[4]提出了一种针对城市环境的搜寻算法对检测器进行导航,与传统搜寻方法相比可大幅度缩短搜索时间。S.Kobayashi等人[5]设计了一种车载辐射检测系统,可快速对大面积区域进行检测,有着较高的精确度。J.Y.Jiang等人[6]通过使用携带辐射检测设备的直升机,采取空中悬停的方式为放射性物质污染区域绘制辐射分布图,并在福岛事故中验证了方案的有效性。Tomas等人[7]开发出一种自主机器人探测系统,通过检测到的辐射特征自动操控地面无人车对辐射源进行定位。

而在某些地形复杂的区域,使用多智能体编队搜寻放射性物质有着不可替代的优势。如在山区或城市建筑群,较于人工搜寻或车载检测系统,多智能体或飞行器编队搜寻有着高效、适用性强等特点。目前已有一些研究成果,如P.Gong等人[8]开发出一种无人机辐射检测系统,使用专门的源定位算法对辐射源进行实时定位。S.Zhu等人[9]采用领导跟随的策略对具有输入约束的无人机组进行编队,对未知的移动辐射源进行搜寻。B.Li等人[10]考虑了使用多旋翼无人机对辐射源进行搜索,针对不同的搜索场景设计了三种不同的搜索算法,并进行了模拟验证,具有成本低,精确度高等特点。J.Han等人[11]将编队控制算法与轮廓映射策略相结合,以递减半径的圆形或方形环来对无人机组进行编队,实现通过多个无人机编队同时进行辐射源搜索与辐射信号场的轮廓映射。但目前大部分研究者仅聚集于辐射源搜寻,并未解决对辐射源实时跟踪监测问题,尤其是多个的动态辐射源。

受文献[12-13]启发,本文设计了三个分布式估算器,分别对智能体极半径、极角以及移动辐射源的几何中心进行估计,利用估计值为智能体设计控制协议。并使用一种新的方法证得多智能体系统将在有限时间内对移动辐射源进行环绕跟踪。最后,通过示例验证了控制方案的准确性。

1 预备知识

1.1 符号说明

符号N*,R+,Rn,Rn×m分别表示正整数、正实数、n维实向量和n×m维实矩阵的集合。记符号1d为所有元素都为1的d行1列的实向量。

1.2 图论

智能体之间的信息交互可以用无向图G=(V,E)来表示,其中V={v1,v2,…,vn}表示图G的节点集,节点vi表示智能体i;E={(vi,vj)}表示图G的边集,边(vi,vj)表示第i个节点与第j个节点能与彼此交互信息。节点i的邻居集定义为Ni={vj∈V:(vi,vj)∈E}。A=[aij]n×n为图G的加权邻接矩阵,A∈Rn×n,其中aij表示节点i到节点j之间边的权值。当(vi,vj)∈E时,aij=aji>0,否则aij=0,并假设智能体本身不存在自循环,即aii=0。图G的Laplacian矩阵定义为L(A)=[lij]n×n,其中

2 问题表述

本文中所描述的多智能体系统由n个智能体与m个移动辐射源组成,智能体i的动力学行为用以下方程表示:

(1)

(2)

(3)

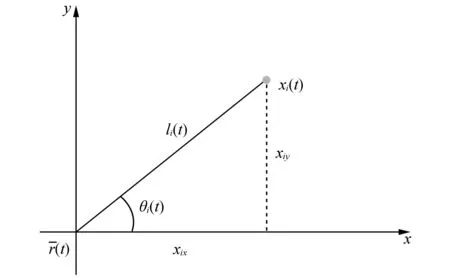
图1 直角坐标与极坐标转换Fig.1 Rectangular coordinate and polar coordinate conversion

(4)

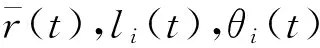
本文的目标是设计一个分布式有限时间控制协议,使得所有智能体在有限时间内对所有移动辐射源形成一个环绕控制圈,将其包围在控制圈内实时监测,并且所有智能体在环绕轨道上实现均匀分布。

定义1：若存在某一有限时间T,使得系统(1)里的智能体满足

(5)

图2 4个智能体环绕跟踪2个辐射源Fig.2 Four agents surround and track two radiation sources

引理1[14]:若β>1,0<α≤1,a1,a2,…,aN≥0,有下列不等式成立:

引理2[15]:若标量系统:

其中n,m,p,q是正整数,并且α,β,γ>0,m>n,q>p。则系统实现有限时间全局稳定,其稳定时间的上界可估计为

引理3[15]:无向连通图G的拉普拉斯矩阵L(A)的最小非零特征值称为代数连通度,用λ2(A)表示,该值大于零且满足

xTL(A)x≥λ2(A)xTx,∀x∈Rn。

引理4[16]:设{λi(t)/i=1,2,…,n}与{τi(t)/i=1,2,…,n}为给定的两个函数集,A=[aij]∈Rn×n为一个给定的矩阵,若aij=aji,则

特别地,若λi(t)=τi(t),i=1,2,…,n,则

若λi(t)=1,i=1,2,…,n,则

3 主要结果

为使多智能体系统在有限时间内对移动辐射源形成环绕跟踪,本文给出以下假设：

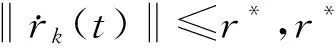
首先，为获得移动辐射源的几何中心，构建了下面分布式估算器:

(6)

然后通过构建分布式估算器(7)对环绕半径进行推断:

(7)

这里的βi1,βi2,βi3,为设计参数且均为正实数,zik(t)=‖rk(t)-ci(t)‖,ρiM(t)为智能体i对d(t)的第M次估计值,若M预先无定义,则M=n。

最后构建了下面分布式估算器,对系统稳定时各智能体的极角进行估算:

(8)

这里的δi1,δi2,δi3为设计参数且均为正实数。

因此,可设计智能体的控制协议为:

(9)

证明:设Lyapunov函数

(10)

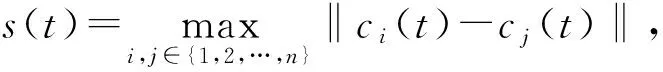
对V1(t)关于t求导得

由引理4可得

(11)

根据引理1可得出

(12)

同理

(13)

根据假设1及假设2可得

(n-1)r*s(t)。

(14)

最后可得出

(15)

结合(11),(12),(13),(14)有

根据引理2可知存在一个有限时间T1>0,使得

且

于是有

且

ci(t)=cj(t),∀t≥T1。

其中

对分布式估算器(6)的第三个等式从1到n求和,得出

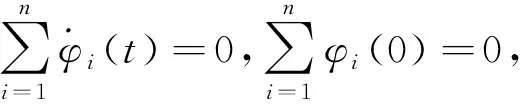
得证。

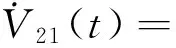
(16)

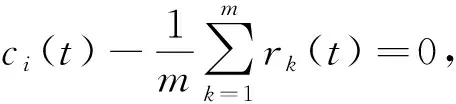
因此

根据引理2可知存在一个有限时间T21>0,使得

其中

其中

由于图G是连通的,可知存在一个有限时间T2M,当t>T2M时有

这里的T2=T2M,由于li(t)=γρiM(t),即证得

且[li(t)-γd(t)]=0,∀t≥T2。

即当t≥T3时,智能体实现均匀分布且具有相同的角速度,其中

(17)

(18)

由引理1,引理4,可得

δi3[e(t)TL(A)e(t)]。

由引理3可得

e(t)TL(A1)e(t)≥λ2[L(A1)]e(t)Te(t)=

2λ2[L(A1)]V3(t)

e(t)TL(A2)e(t)≥λ2[L(A2)]e(t)Te(t)=

2λ2[L(A2)]V3(t)

e(t)TL(A)e(t)≥λ2[L(A)]e(t)Te(t)=

2λ2[L(A)]V3(t)

则

由引理2可知,存在一个T3>0,当t≥T3时有

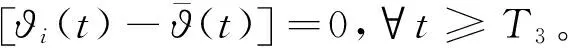
于是有

且ϑi(t)=ϑj(t),∀t≥T3。

其中

由ϑi(t)的定义可知

得证。

定理1:若多智能体系统(1)满足假设1与假设2,根据分布式估算器(6)、(7)、(8)以及控制协议(9),当αi1>(n-1)r*,βi1>2r*,存在一个有限时间T=max {T2,T3},当t>T,多智能体系统稳定,各智能体对所有辐射源实现环绕跟踪并在轨道均匀分布。

证明:由引理5可得

由引理6可知

[li(t)-γd(t)]=0,∀t≥T2。

由引理7得出

得证。

4 仿真

取一个具有4个移动辐射源(T1-T4),6个智能体(A1-A6)的多智能体系统实例,连通情况如图3所示。

图3 多智能体系统的通信拓扑Fig.3 Communication topology of multi-agent system

设智能体的初始位置为x1(0)=[6,-1]T,x2(0)=[-3,2]T,x3(0)=[5,-4]T,x4(0)=[2,-5]T,x5(0)=[-4,3]T,x6(0)=[-6,5]T。

同时,设移动辐射源的动力学方程为:

r1(t)=[-0.5e-t-cost,0.5e-t+sint]T,

r2(t)=[0.5e-t-cost,0.5e-t-sint]T,

r3(t)=[-0.5e-t+cost,-0.5e-t+sint]T,

r4(t)=[0.5e-t+cost,-0.5e-t-sint]T。

取期望角速度ω(t)=1,设计参数αi1=6,αi2=1,αi3=1,βi1=5,βi2=1,βi3=1,δi1=1,δi2=1,δi3=1,γ=2。

由图4与图5可知,移动辐射源的几何中心的估算值在大约0.5 s时收敛到实际值;由图6可知,各智能体大约在1 s时实现均匀分布且具有相同的角速度,每个智能体之间的间隔为0.332π;由图7可知,各智能体的环绕半径大约在0.7 s时收敛一致,并于2.5 s时达到期望值。由图8～图11可知,在控制协议9的控制下,多智能体系统在大约4 s时对移动辐射源实现环绕跟踪,并保持稳定。

图4 辐射源几何中心横坐标估计值Fig.4 Estimated value of the abscissa of the geometric center

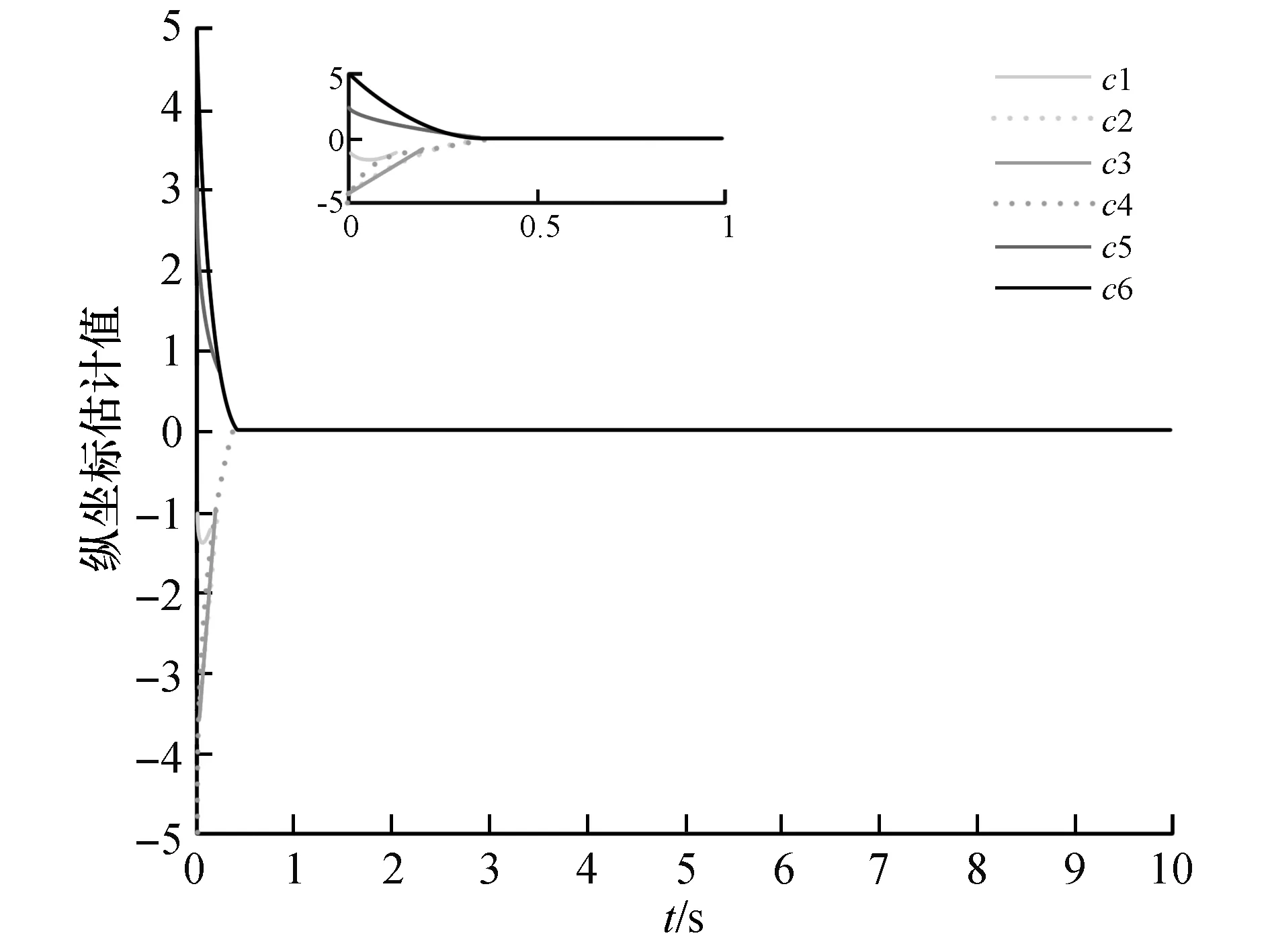
图5 辐射源几何中心纵坐标估计值Fig.5 Estimated value of ordinate of geometric center

图6 智能体极角估计值Fig.6 Estimation of the polar angle of the agent

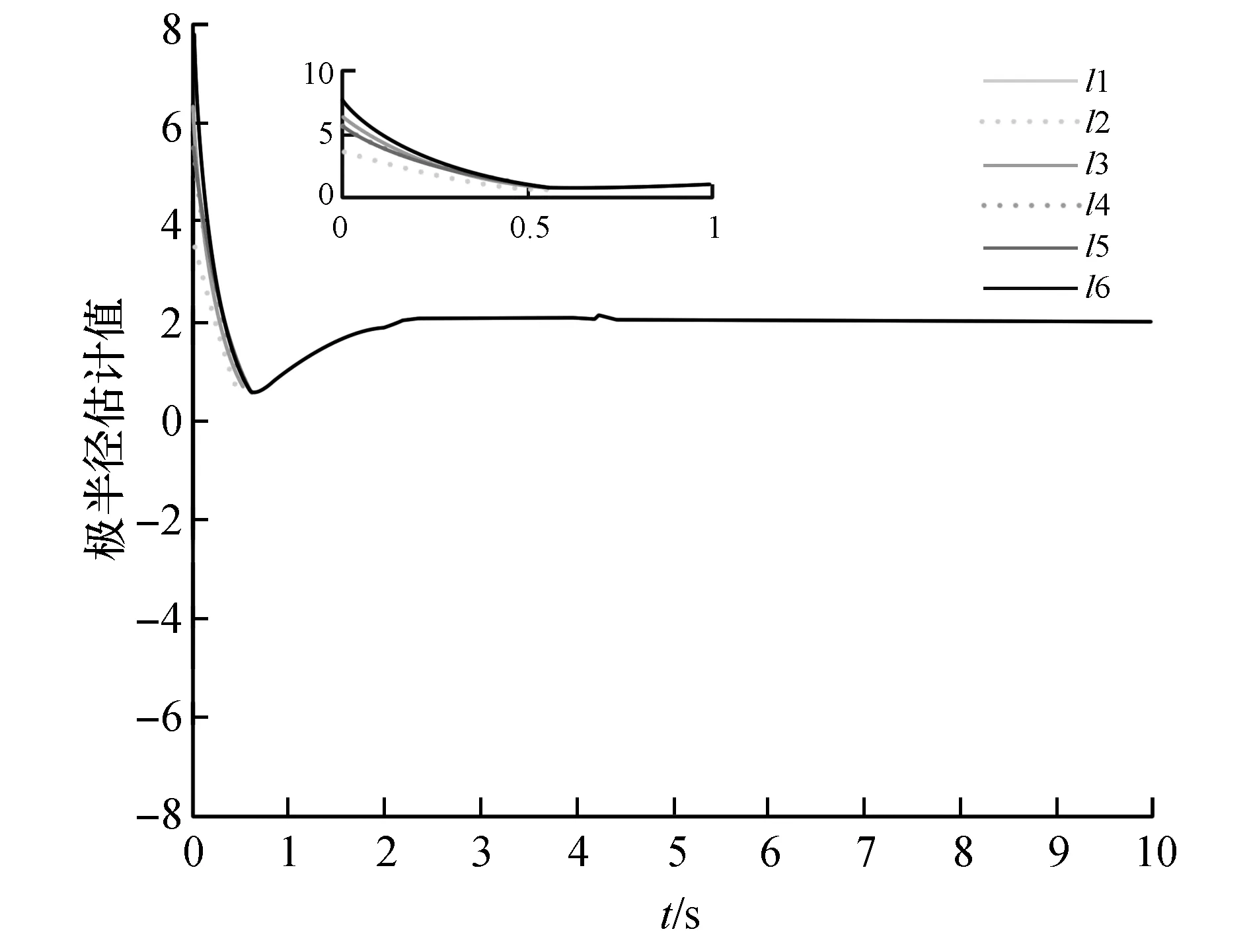
图7 智能体环绕半径估计值Fig.7 Estimation of the circle radius of the agent

图8 2 s时智能体对辐射源的环绕跟踪Fig.8 Surround tracking of the radiation source by the agent at 2 s

图9 4 s时智能体对辐射源的环绕跟踪Fig.9 Surround tracking of the radiation source by the agent at 4 s

图10 6 s时智能体对辐射源的环绕跟踪Fig.10 Surround tracking of the radiation source by the agent at 6 s

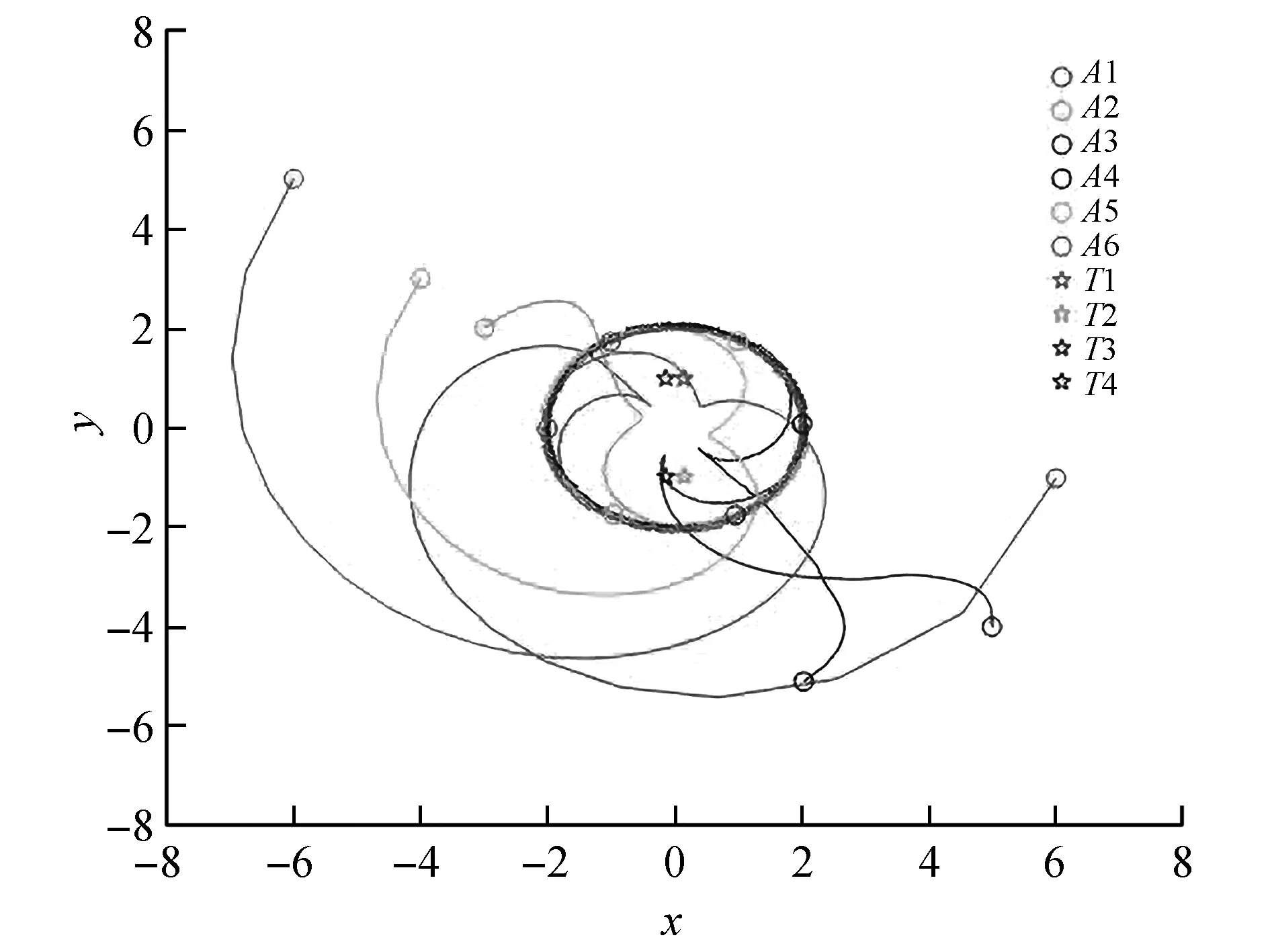
图11 8 s时智能体对辐射源的环绕跟踪Fig.11 Surround tracking of the radiation source by the agent at 8 s

5 结 论

本文对多智能体系统有限时间环绕跟踪作出了研究,分别通过设计三个不同的分布式估算器,估算出智能体的环绕半径、极角、以及移动放射性辐射源的几何中心的精确值,根据估算值设计一个分布式控制协议,以满足环绕跟踪的条件。最后,通过稳定性定理证得对所有移动辐射源的环绕跟踪将在有限时间内完成,解决了多智能体系统在有限时间内对多个动态辐射源的环绕跟踪问题,较于人力搜寻监测有着安全性高、适用性强等优点,有很强的实际意义。