社区居家养老服务供应链定价及协调策略研究：考虑老年人服务偏好

任宗伟 刘钰冰 周广民

一 引言及文献综述

近年来，随着老龄化程度的不断加深和经济的迅速发展，老年人服务需求的异质性和多样化在养老产业中越来越凸显(沈超等，2016[1]；Gregory et al., 2017[2])，特别是银发消费水平持续攀升(宋健，2020)[3]，表明老年人对养老服务价格和质量等的重视，更加关心自身的满意度情况，养老服务问题逐渐上升为全社会关注的热点问题之一。习近平总书记在主持就我国人口老龄化的形势和对策举行的第三十二次集体学习中强调，要重视养老服务行业的发展。根据国务院颁发的《关于全面放开养老服务市场提升养老服务质量的若干意见》等系列养老服务政策，要加大养老服务市场的开放力度，积极转变养老服务的供给结构，利用供应链的模式提高养老服务质量水平，有效提升老年人的满意度。而体量巨大且具有个性的老年人群体受到传统“落叶归根”、“家庭养老”思想的影响，加之目前国内的机构养老模式不能满足老年人异质性和多样化的需求，以居家养老为基础、社区进行托底服务的社区居家养老服务供应链模式成为我国未来主要的养老模式。这既解决了老年人对在家养老的诉求，又满足了其不同的服务需求偏好，深得广大老年人的青睐。

现有关于养老服务供应链的研究主要涉及供应链主体的选择、服务质量决策分析、服务风险识别、服务资源整合等方面。张智勇等(2014)[4]把成本和服务质量的因素考虑进去，建立了双层规划模型来选择养老服务提供商。在服务质量决策分析方面，张智勇等(2013)[5]以养老服务集成商为研究对象，研究单个或多个养老服务集成商在不同的市场规模下如何通过博弈获得最优服务质量决策的问题，并讨论需求规模差异下养老服务提供商的质量决策和最优服务质量决策之间的影响关系(张智勇等，2015)[6]，以及养老服务供应链各主体在单独、联合决策以及利用奖惩契约不同情形下的质量博弈(张智勇等，2016)[7]。在服务风险识别方面，张智勇等(2015)[8]通过支持向量机模型对养老服务供应链的质量风险做定性分析，识别影响质量风险的关键因素；马跃如等(2020)[9]利用扎根理论分析养老服务供应链各主体面对的主要风险，提出增强养老服务供应链稳定性的建议。在服务资源整合方面，袁竞峰等(2019)[10]运用不完全契约理论，构建社会资本参与社区养老模式决策理论模型，分析影响社区养老模式决策的关键性因素；李士梅和高维龙(2018)[11]基于交易成本理论研究养老服务市场的契约治理机制和作用机理；王建云和钟仁耀(2019)[12]运用魅力质量理论Kano模型和Topsis法分析了老年人社区居家养老服务需求层次，提出应构建从下而上的社区居家养老服务供给决策模式；曲绍旭和郑英龙(2020)[13]基于服务资源整合的视角，分析了社区居家养老服务存在的供需失衡问题，提出要优化养老政策链条，推动供需平衡循环，促进供需平衡政策的产出。

一些学者还研究了政府补贴对养老服务供应链的影响。桑秀丽等(2016)[14]运用Stackelberg博弈理论研究政府补贴下的养老服务供应链资源分配。高晓波和孙行臻(2018)[15]利用两阶段博弈的方法分析政府补贴和服务质量差异下的社区居家养老服务机构决策。杨韡韡等(2018)[16]从特征价格视角对养老机构价格进行实证分析，发现合理的政府补贴对养老机构定价非常关键。郭倩和王效俐(2018)[17]建立了首先为政府确定补贴力度，然后为养老机构确定服务质量水平，再基于政府补贴力度和养老服务质量水平为养老机构确定服务价格的三阶段博弈模型，得出适当的政府补贴力度有利于实现养老服务社会收益最大化的结论。进一步地，其考虑政府补贴，建立了不同性质养老机构服务动态供给模型，分析不同补贴力度和方式对养老服务市场供给量产生的影响(郭倩和王效俐，2020)[18]。上述文献为本文的研究奠定了基础，但侧重从养老服务供应链供给方角度出发，较少从需求方即老年人视角思考老年人需求满足对养老服务供应链整体的影响，同时考虑供应链主体行为因素对决策影响的研究也较少。探讨老年人行为因素对养老服务供应链运作效率的影响是养老产业高质量发展中亟待解决的问题。

鉴于此，本文以需求为导向，考虑老年人服务偏好，在社区居家养老服务供应链中引入老年人满意度，构建包括养老服务提供商、社区居家养老服务中心和老年人在内的三方动态博弈模型，分析老年人的服务偏好对老年人满意度以及社区居家养老服务的影响。此外，对比集中和分散两种决策模式下各主体的最优定价策略和最优服务质量水平决策，再探讨“收益共享+质量成本共担”契约机制的协调效应。

二 模型构建

(一)问题描述与假设

老年人是养老服务供应链定价与协调中的重要主体。本文研究由养老服务提供商、社区居家养老服务中心和老年人组成的三级服务供应链。在社区居家养老服务供应链运作过程中，养老服务提供商提供养老服务并进行服务质量决策；社区居家养老服务中心依据市场需求和养老服务提供商的协议价格确定养老服务价格；老年人根据自身对服务价格和服务质量的偏好，确定对社区居家养老服务的需求量。社区居家养老服务供应链运作模式如图1所示。

图1 社区居家养老服务供应链运作模式

养老服务提供商提供单位养老服务的固定成本为c；社区居家养老服务中心以协议价格w从养老服务提供商处获得养老服务；社区居家养老服务中心以服务价格p向老年人提供养老服务。

符号的含义：下标sp表示养老服务提供商，下标sc表示社区居家养老服务中心，下标ss表示整个社区居家养老服务供应链，上标c表示集中决策，上标d表示分散决策，上标r表示契约协调，X*表示X的最优值。

相关主要变量符号及其含义如表1所示。

表1 模型主要变量说明

为便于分析，本文提出以下假设：

(1)社区居家养老服务供应链上的所有信息是完全对称的。养老服务提供商与社区居家养老服务中心都是完全理性的个体，且风险偏好均为中性，养老服务提供商充分了解老年人的服务偏好，能够提供满足老年人不同服务需求的养老服务。

(2)由于老年人对服务价格和服务质量有不同的偏好，依据敏感系数不同，将老年人划分为经济型老年人、中性老年人和品质型老年人三种类型。比起服务的质量，经济型老年人更加注重服务的价格，对服务价格的敏感程度大于对服务质量的敏感程度，即σ>μ；中性老年人把服务价格和服务质量看作是一样重要的，没有先后之分，对服务价格的敏感程度与对服务质量的敏感程度相同，即σ=μ；比起服务的价格，品质型老年人更加注重服务的质量，对服务价格的敏感程度小于对服务质量的敏感程度，即σ<μ。

(二)构建老年人满意度函数

老年人满意度为自身对服务的心理价值感知程度，考虑老年人满意度大小受服务价格、需求数量、服务质量以及购买养老服务后的可支配收入因素影响。如果老年人是完全理性的，服务价格越低、服务数量越多、服务质量越好，老年人对服务的心理价值感知程度就越高，那么老年人满意度就越大。因此，本文根据柯布道格拉斯生产函数构造了老年人满意度函数(刘新民等，2018)[19]：

(1)

s.t.z=(N-pq)≥0

(2)

这里，σ表示老年人对服务价格的敏感系数；μ表示老年人对服务质量的敏感系数；θ表示老年人从购买养老服务后的可支配收入中得到满足感的敏感系数；z表示老年人购买养老服务后的可支配收入；N表示老年人的收入水平；F表示老年人满意度。

(3)

再将式(3)代回式(1)，进而得出养老服务需求量为q*时老年人最大满意度为:

(4)

引理1：老年人满意度和服务价格呈现出负相关关系，和服务质量呈现出正相关关系。

三 基本决策模型

(一)集中决策下供应链模型

在集中决策模式下，养老服务提供商和社区居家养老服务中心被看作是利益的共同体。这时，以社区居家养老服务供应链系统整体利润最大化为目标是对他们最佳的决策模式。集中决策下供应链模型为：

(5)

(6)

(7)

将pc*、mc*代入式(3)，可得集中决策下老年人最优需求量为：

(8)

再将式(8)代入式(4)，可得集中决策下老年人满意度为:

(9)

因此，可得集中决策下整个社区居家养老服务供应链的最大利润为:

(10)

(二)分散决策下供应链模型

在分散决策模式下，养老服务提供商和社区居家养老服务中心都是独立决策的利益体，对他们来说，最佳的决策模式就是使自己的利润达到最大。建立养老服务提供商为主导的Stackelberg博弈模型，首先养老服务提供商根据服务成本、市场需求以及自身情况向社区居家养老服务中心报价，然后社区居家养老服务中心结合自身的情况做出反应并确定服务价格。

基于此模式下的决策时序，采用逆向归纳法进行求解，供应链模型为：

(11)

(12)

由假设(1)可知，养老服务提供商面对的市场需求满足q=q*，将式(3)代入式(11)、 式(12)，则养老服务提供商和社区居家养老服务中心的利润分别为：

(13)

(14)

(15)

(16)

(17)

将式(16)、 式(17)代入式(15)和式(3)，得到分散决策下最优服务价格和最优需求量分别为：

(18)

(19)

再将pd*、qd*代入式(4)，可得分散决策下老年人满意度为：

(20)

将pd*、md*、wd*代入式(13)和式(14)，可得分散决策下养老服务提供商和社区居家养老服务中心的最大利润分别为:

(21)

(22)

引理2：养老服务价格和协议价格与老年人的服务质量敏感系数无关，与老年人的服务价格敏感系数呈现负相关关系。

由引理2可知，对于理性老年人来说，随着老年人对服务价格敏感程度的增大，服务价格不断降低。因此，如果想让老年人满意度不断提高，则需要不断降低服务价格。

(三)集中决策与分散决策对比

推论1：集中决策下pc*比分散决策下pd*低。

推论2：集中决策下mc*比分散决策下md*高。

从推论1-推论3可以看出，分散决策下养老服务价格高于集中决策，而服务质量水平却低于集中决策，且集中决策下供应链各主体利润和比分散决策下大。这表明在分散决策下供应链系统中存在“双重边际”效应，无法实现供应链利润的最大化。通过调查研究发现，“收益共享+成本共担”契约比价格折扣、数量折扣、回购等契约更具有实用性。因此，养老服务市场可引入“收益共享+质量成本共担”契约减少供应链系统中的“双重边际”效应，进行供应链的协调。

四 供应链契约协调

根据推论1-推论3可知，分散决策下养老服务提供商的最优服务质量水平比集中决策下的低，而最优服务价格却高于集中决策。如果使分散决策下的最优服务质量水平和最优服务价格能够和集中决策下的水平一样，那么养老服务提供商需要加强服务质量成本投入，但却没有足够的动力。因此，为了达成供应链主体间的合作，实现供应链系统的稳定，在保证各主体利润提升的同时，需做出最佳的全局最优决策。由于社区居家养老服务中心会分担一部分成本投入，设社区居家养老服务中心分担的质量成本投入比例为Φ∈(0, 1)，养老服务提供商给予社区居家养老服务中心协议价格折扣，进而使得社区居家养老服务中心降低最优服务价格。同时，养老服务提供商需要将自己的部分收益φ∈(0, 1)分享给社区居家养老服务中心，假设社区居家养老服务中心收益共享后自身占有的利润比例为φ∈(0, 1)。由此得到养老服务提供商和社区居家养老服务中心的利润函数：

(23)

(24)

与分散决策下推导过程相同，可得：

(25)

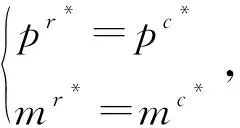
(26)

(27)

由命题1可知，社区居家养老服务中心分担养老服务提供商的一部分质量成本投入，养老服务提供商给予社区居家养老服务中心协议价格折扣并且将自身的部分收益分享给社区居家养老服务中心，能够使得供应链的最优服务价格和最优服务质量水平达到集中决策下的最优水平，进而达成各主体共赢的局面，有效实现供应链的协调。

将式(25)代入式(3)，可得契约协调下最优服务需求量为：

(28)

再将式(28)代入式(4)，可得契约协调下老年人的满意度为：

(29)

命题2：在命题1的契约协调情况下，社区居家养老服务中心不改变定价策略，而养老服务提供商提高服务质量水平后，供应链以及供应链中各主体利润都受到一定程度的影响，但是有效增加了老年人满意度。

由命题2可知，大多数社区居家养老服务中心在经营时加大质量成本的投入，提高服务质量水平，会加深老年人对养老服务的认可度，使老年人形成消费习惯，增加其服务需求黏性，有效提高老年人的满意度，进而保持稳定的市场占有率。

五 数值分析

下面进一步检验本文结论的正确性和契约协调的有效性。以哈尔滨某社区居家养老服务中心为案例背景，进行数值分析。该中心主要为老年人提供日常照料、助餐、棋牌娱乐、免费阅读、书画交流等服务，中心服务老年人数量为240人，老年人的平均退休工资为5200元。按照是否收取费用，服务分为无偿类、低偿类和有偿类，本文重点研究有偿类服务项目，为此给出有偿类服务信息，如表2所示。

表2 哈尔滨某社区居家养老服务中心有偿类服务信息

结合实际调研及上述服务信息，选择助医服务为数值模拟分析对象，服务时间为3小时，服务过程如下：由老年人提出助医需求申请，然后由社区居家养老服务中心联系合作的医疗服务机构，再由医疗服务机构派人员到家提供助医服务。对模型的主要参数进行赋值：A=1，θ=0.01，N=5200，γ=0.1，c=20元/小时。利用MATLAB软件求解模型并进行仿真分析。

(一)集中决策与分散决策下数值分析

1.老年人服务偏好对老年人满意度影响

保持其他模型参数不变，考虑两种决策模式下老年人对服务价格的敏感系数与老年人对服务质量的敏感系数对三种类型老年人满意度的影响情况，进行灵敏度分析。由图2可以看出，在两种决策模式下，老年人满意度与老年人对服务价格的敏感系数呈负相关关系，与老年人对服务质量的敏感系数呈正相关关系；品质型老年人满意度最高，经济型老年人满意度最低；当σ取值越小，μ取值越大时，老年人满意度达到最大值。但不管变化趋势如何，都能够看出分散决策下的老年人满意度始终小于集中决策下的老年人满意度。

图2 老年人服务偏好对老年人满意度的影响 图3 老年人服务偏好对服务价格的影响

2.老年人服务偏好对各决策变量与利润的影响

由图3可知，随着σ取值越大，老年人对服务价格越来越敏感，服务价格呈下降的趋势。但不管变化趋势如何，都能够看出分散决策下的服务价格大于集中决策下的服务价格。

由图4、图5可知，随着σ和μ取值越大，老年人对服务价格和服务质量越来越敏感，服务质量水平、服务需求量呈上升的趋势。但不管变化趋势如何，都能够看出分散决策下的服务质量水平、服务需求量小于集中决策下的服务质量水平、服务需求量。

图4 老年人服务偏好对服务质量水平的影响 图5 老年人服务偏好对服务需求量的影响

由图6可知，随着σ和μ取值越大，老年人对服务价格和服务质量越来越敏感，集中决策下供应链总利润呈上升的趋势。由图7可知，随着σ和μ取值越大，老年人对服务价格和服务质量越来越敏感，分散决策下养老服务提供商和社区居家养老服务中心的利润均呈上升的趋势，并且社区居家养老服务中心的利润明显高于养老服务提供商的利润。

图6 老年人服务偏好对供应链总利润影响 图7 分散决策下老年人服务偏好对利润的影响

(二)供应链协调下数值分析

在满足命题1的情况下能够实现供应链的协调，由假设(2)可知，经济型老年人、中性老年人和品质型老年人可以用σ和μ的相对取值来表示。经济型老年人更加注重服务价格(σ=0.6,μ=0.4)；中性老年人对服务价格和服务质量同等重视(σ=0.5,μ=0.5)；品质型老年人更加注重服务质量(σ=0.4,μ=0.6)。经计算得出供应链协调下各参数的结果，如表3所示。

表3 供应链协调下数值分析

从表3可以看出，设计的供应链契约协调对所有类型老年人都是有效的，集中决策下最优定价更低，以中性老年人(σ=0.5,μ=0.5)为例，老年人对服务价格和服务质量同样敏感，社区居家养老服务中心以自身利润最大化为原则的最优定价为22.5，而在供应链契约协调下的最优定价为15，对于老年人来讲，能够以更低的价格获得同样的服务。社区居家养老服务中心利润为：

若要保证社区居家养老服务中心愿意参与供应链协调，则需要保证68.59φ>18.06，即φ>0.263，这说明只要保证社区居家养老服务中心的收益共享比例大于0.263，就能够降低服务价格，进而达成主体间合作，实现供应链的协调。此时养老服务提供商利润为：

为了确保养老服务提供商也愿意参与供应链协调，则需要保证68.59(1-φ)>6.02，即φ<0.912，综上所述，当0.263<φ<0.912时能够实现供应链协调，φ取值越大，社区居家养老服务中心的利润越大。

如图8和图9所示，以中性老年人为例，观察收益共享比例和质量成本共担比例对养老服务提供商和社区居家养老服务中心利润的影响。从图8可以看出，随着φ取值越大，养老服务提供商利润减小；随着φ取值越大，养老服务提供商利润增大。从图9可知，随着φ和φ取值越大，社区居家养老服务中心利润增大。在供应链协调情况下，保证收益共享比例和质量成本共担比例在一个合理区间的同时，养老服务提供商和社区居家养老服务中心能够达成合作，有效地实现供应链的协调。

图8 收益共享比例和质量成本共担比例对养老服务提供商利润的影响(σ=0.5, u=0.5) 图9 收益共享比例和质量成本共担比例对社区居家养老服务中心利润的影响(σ=0.5, u=0.5)

六 结论与建议

本文基于老年人满意度视角，考虑老年人服务偏好，通过建立老年人满意度函数，探讨了养老服务提供商、社区居家养老服务中心和老年人所组成的社区居家养老服务供应链定价及协调问题。运用Stackelberg博弈分析供应链主体间的最优决策，并对集中和分散两种决策模式下各主体的最优决策进行比较。为促使养老服务提供商提高服务质量水平，社区居家养老服务中心降低服务价格，构建“收益共享+质量成本共担”契约进行供应链协调是有效的，可以增加老年人满意度。结论及对养老服务供应链各主体的启示为：

1.考虑老年人服务偏好，社区居家养老服务供应链中，老年人满意度和服务价格呈现出负相关关系，和服务质量呈现出正相关关系。服务价格与价格敏感系数负相关，与服务质量敏感系数无关。而且老年人服务偏好也会影响自身的满意度。这不仅为养老服务行业管理者提供一定的决策参考，还有利于社区居家养老服务供应链的进一步研究。

2.老年人服务偏好在一定区间时，养老服务提供商、社区居家养老服务中心和整个社区居家养老服务供应链都可以取得最优利润。因此，养老服务提供商和社区居家养老服务中心都应该充分了解老年人的服务偏好。每个老年人拥有的不同服务偏好对供应链产生了不一样的影响。因而，养老服务提供商应在满足老年人服务偏好的前提下提供养老服务，再由社区居家养老服务中心根据自身的实际情况对养老服务进行定价，以便为老年人提供最适合的养老服务，进而达成各主体共赢的局面。

3.分散决策下养老服务价格高于集中决策，而养老服务质量水平却比集中决策低，并且分散决策下供应链各主体利润和比集中决策下小。由此说明，分散决策下存在“双重边际”效应，这为供应链带来了较低的服务质量水平和较高的养老服务价格，使得整个社区居家养老服务供应链的利润没有达到最大化。因此，社区居家养老服务中心在提供服务过程中需要加深老年人对养老服务的认可度，使老年人形成消费习惯，增加其服务需求黏性，有效提高老年人的满意度，进而保持稳定的市场占有率。

4.社区居家养老服务供应链各主体间需要加强合作。通过制定合适的“收益共享+质量成本共担”契约进行供应链协调，既能够有效促进养老服务提供商和社区居家养老服务中心达成合作，又可以保证提高双方的利润。此外，利用设计的“收益共享+质量成本共担”契约进行供应链协调，还能够降低养老服务的定价，提高养老服务质量水平，进而提升老年人的满意度。