一道高考题再议圆锥曲线中直线过定点问题

■湖北省沙市第七中学

求解直线或圆锥曲线过定点问题是近几年高考的热点题型。同学们解决直线与圆锥曲线的位置关系的思想方法，体现出大家的数学核心素养。2020 年全国高考Ⅰ卷文科卷第21题就是过定点问题，我们借此机会再次研究这类问题，探讨这类热点问题的解决方法与技巧。

一、问题重现

例1(2020年全国Ⅰ卷)已知A、B分别为椭圆E：+y2=1(a＞1)的左、右顶点，G为椭圆E的上顶点，=8，P为直线x=6上的动点，PA与椭圆E的另一交点为C，PB与椭圆E的另一交点为D。

(1)求椭圆E的方程；

(2)证明：直线CD过定点。

解析：依据题意作出图1。

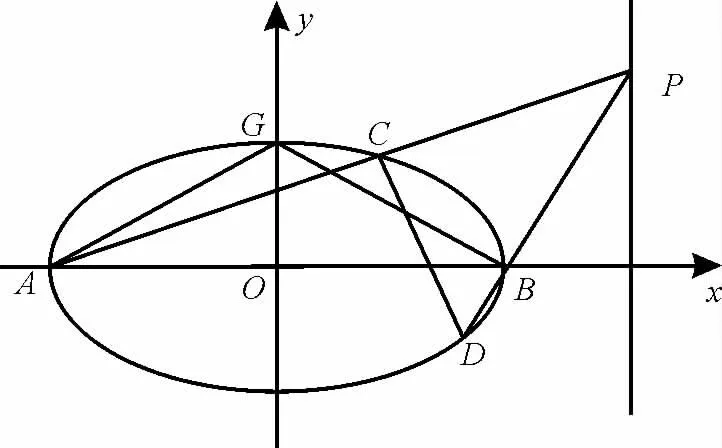
图1

(2)设P(6，y0)，则直线AP的方程为y=，即y=(x+3)。

联立直线AP的方程与椭圆方程：。

(1)求椭圆C的方程。

(2)点M，N在椭圆C上，且AM⊥AN，AD⊥MN，D为垂足。证明：存在定点Q，使得|DQ|为定值。

解析：依据题意作出图2。

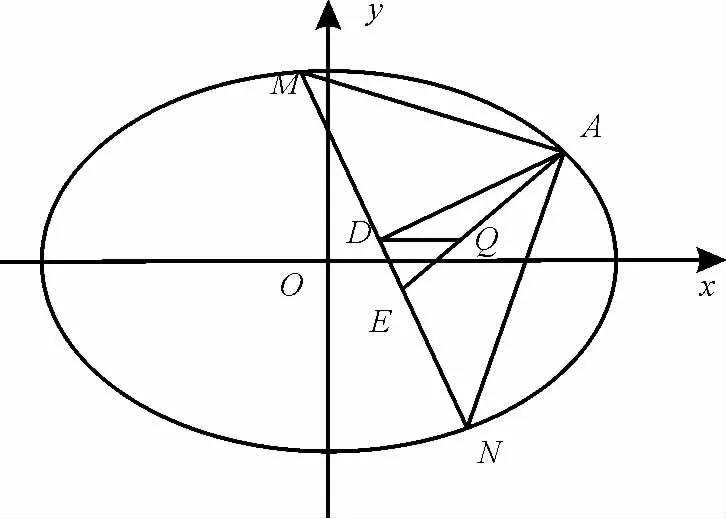
图2

(2)设 点M(x1，y1)，N(x2，y2)。因 为AM⊥AN，所以=-1。

例3(2018 年新课标)设椭圆C：+y2=1的右焦点为F，过F的直线l与椭圆C交于A，B两点，点M的坐标为(2，0)。

(1)当直线l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB。

解析：(1)答案略。

(2)当直线l与x轴重合时，∠OMA=∠OMB=0°。

当直线l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB。

当直线l与x轴不重合也不垂直时，设直线l的方程为y=k(x-1)(k≠0)，A(x1，y1)，B(x2，y2)。

二、方法与技巧

解此类题的常见方法是联立消元法。依题目条件设出相关参数，如设出直线的斜率截距；求出直线方程，联立直线与圆锥曲线，利用根与系数的关系，把直线与圆锥曲线方程中的变量x，y看成常数，把方程的一端化为零，将方程转化为以参数为主变量的方程。这个方程对任意参数都成立，这时参数的系数就要全部等于零，这样就得到一个关于x，y的方程组，这个方程组的解所确定的点就是直线或圆锥曲线所过的定点。

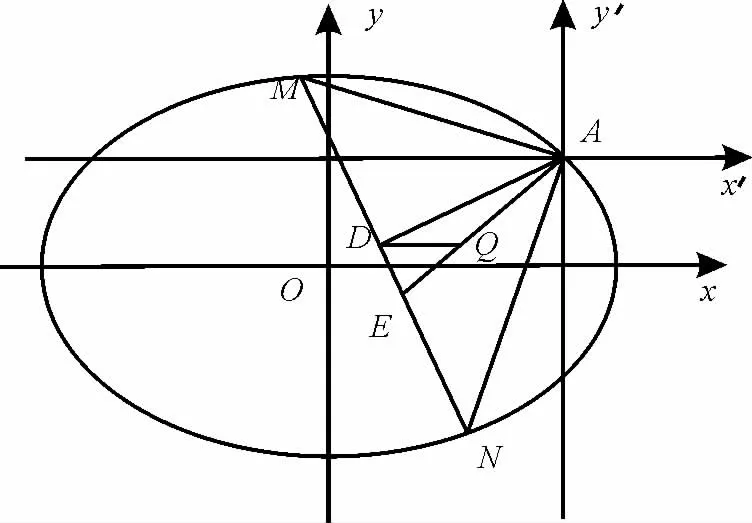
图3

联立消元方法是解决这一类问题的常见方法，需要一定的运算技巧与运算量。我们是否可以尝试一下别的运算技巧与方法? 尤其在题目条件中给出斜率之积或之和时，不妨用这种构造齐次式的方法。下面用此法解2020年新高考的第22题，具体方法与步骤如下。

过一个定点P作两条直线与圆锥曲线交于A、B两点，在直线PA和PB斜率之和或斜率之积为定值的情况下，直线AB过定点问题，可以利用平移构造齐次式的方法秒杀。只是要注意构造齐次时巧妙利用直线方程mx+ny=1，需要一次直接乘，需要二次可以将其平方再乘。接着将齐次式两边同时除以x2，整理为关于k的一元二次方程，从而由韦达定理得到两斜率之和或之积的表达式，整理成关于m，n的关系式，就可以知道平移后的直线过定点，那么原来的直线过定点也就一目了然。

定点问题是常见的出题形式，化解这类问题的关键就是引进参数表示直线方程、数量积、比例关系等，根据等式恒成立、数式变换等寻找不受参数影响的量。直线过定点问题通法是联立消元法，设出直线方程，通过韦达定理和已知条件找出斜率和截距的一次函数关系式，代入直线方程即可。只是计算量比较大，演算过程比较麻烦，这便成为很多同学畏惧不前的障碍。如果能够从圆锥曲线、直线的方程的结构特征出发，采取齐次式的转化，那么解题必然会事半功倍，柳暗花明！