扫描圆锥曲线常见的易错点

■广东省汕头市澄海凤翔中学

易错点1 忽视动点坐标的设法致错

例1设线段AB的两个端点A、B分别在坐标轴上滑动，且|AB|=4，点P是线段AB的中点，则点P的轨迹方程是( )。

A.x2+y2=16 B.x2+y2=4

C.x2-y2=16 D.x2-y2=4

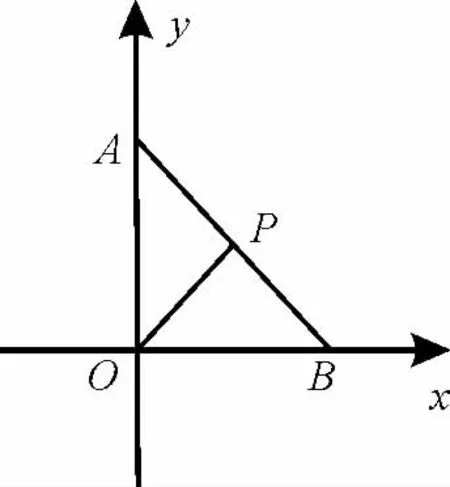
图1

错解：如图1 所示，设A(0，y)，B(x，0)。由中点坐标公式可得点P的坐标为，连接OP，由直角三角形斜边上的中线性质可得|OP|=|AB|=2。所以=4，即x2+y2=16。因此，点P的轨迹方程是x2+y2=16，选A。

错因剖析：求轨迹方程，即求轨迹上任意一点的坐标所满足的方程，并检验以方程的解为坐标的点是否都是轨迹上的点，因此，应设轨迹上任意一点的坐标为(x，y)。上述解法是因为动点坐标设的不对，即运用方法不当而导致错误。

正解：设中点P(x，y)，A(0，m)，B(n，0)，则m=2y，n=2x。因为|AB|=4，所以n2+m2=16，(2x)2+(2y)2=16，即x2+y2=4。因此，点P的轨迹方程是x2+y2=4，选B。

易错点2 忽视定义中的条件致错

例2若点M到两定点F1(0，-1)，F2(0，1)的距离之和为2，则点M的轨迹是( )。

A.椭圆

B.直线F1F2

C.线段F1F2

D.线段F1F2的中垂线

错解：根据椭圆的定义可知，点M的轨迹是椭圆，故选A。

错因剖析：在椭圆的定义中，点M到两定点F1，F2的距离之和必须大于两定点的距离，即|MF1|+|MF2|＞|F1F2|，亦即2a＞2c。而本题中|MF1|+|MF2|=|F1F2|，所以点M的轨迹不是椭圆，而是线段F1F2。

正解：因为点M到两定点F1(0，-1)，F2(0，1)的距离之和为|F1F2|，所以点M的轨迹是线段F1F2，选C。

易错点3 忽视标准方程的特征致错

例3已知抛物线y=mx2(m≠0)的准线与直线y=1的距离为3，则抛物线的标准方程是_____。

易错点4 忽视隐含条件致错

例4已知正方形ABCD的顶点A、B在抛物线y2=x上，顶点C、D在直线y=x+4上，求正方形的边长。

错因剖析：在考虑直线AB与抛物线相交时，方程y2-y+b=0的判别式Δ＞0，以此来限制b的取舍。

易错点5 忽视焦点位置的讨论致错

例5已知抛物线的焦点F在x轴上，点A(m，-3)在抛物线上，且|AF|=5，则抛物线的标准方程为____。

错解：因为抛物线的焦点F在x轴上，且点A(m，-3)在抛物线上，所以抛物线的标准方程可设为y2=2px(p＞0)。设点A到抛物线准线的距离为d，则d=|AF|=

所以抛物线的标准方程为y2=2x或y2=8x。

错因剖析：当抛物线的焦点位置无法确定时，需分类讨论。

正解：因为抛物线的焦点F在x轴上，且点A(m，-3)在抛物线上，所以当m＞0时，点A在第四象限，抛物线的标准方程可设为y2=2px(p＞0)。

所以抛物线的标准方程为y2=2x或y2=8x。

当m＜0时，点A在第三象限，抛物线的标准方程可设为y2=-2px(p＞0)。

所以抛物线的标准方程为y2=-2x或y2=-8x。

综上所述，抛物线的标准方程为y2=2x或y2=8x或y2=-2x或y2=-8x。