二维电磁亥姆霍兹腔中回音壁模式研究

王倩婧,杜骏杰

（华东师范大学 物理与电子科学学院, 上海 200241）

0 引 言

英国伦敦的圣保罗大教堂和北京的天坛, 都有一个环形的长廊. 在这个长廊里对着墙壁轻声说话,即使另一个站在长廊里的人与之相距很远, 也能够听得清说话内容, 因此人们把这样的长廊称为“耳语回廊”. 早在1910年, Raleigh[1]就对这一现象进行了解释, 他认为声波在回廊中传播时, 在墙壁上发生了连续反射, 使声音可以沿回廊传播很远, 并且在传播过程中损耗很小. 他把这种声波的传播模式命名为“耳语回廊模式”(Whispering-Gallery Mode, WGM), 或称为回音壁模式. 图1示意性地展示了回音壁模式被激发时, 声波在腔体内表面发生连续全反射从而传播. 如果声波在腔体内传播1周增加的相位是 2π 的整数倍, 那么腔体内的波将相互叠加增强, 形成回音壁模式.

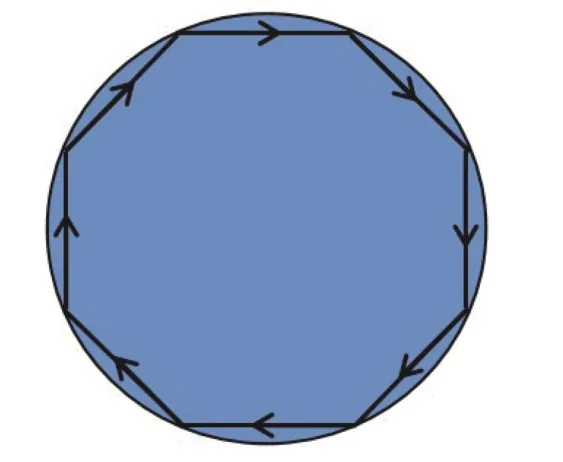
图1 在一个封闭的腔内激发的回音壁模式的示意图Fig. 1 Schematic demonstration of whispering gallery modes excited in a closed cavity

对回音壁模式的研究虽然起源于声波, 但后来在电磁领域的研究中发现电磁波也可以激发类似的模式. 早在1908年, 德国物理学家Mie[2]就在理论上对球形腔的电磁散射进行了研究, 并且给出了散射系数等重要参数的表达式, 为以后电磁回音壁模式的研究奠定了理论基础. 1939年, Richtmyer等[3]通过理论分析, 认为在球形的微型谐振腔中存在高品质因子(Q值)的谐振模式. 但受限于当时的技术水平, 直到1961年Garrett等[4]用CaF2制备了微波谐振腔, 首次在实验中实现了回音壁模式的激光,这一发现吸引了越来越多的研究者开始关注回音壁模式诱导的高Q值谐振腔. 在随后的1963年,Walsh等[5]在红宝石(ruby)环形谐振器中观察到了脉冲形式的回音壁模式激光. 在1990年代初期,Mccall等[6]、Slusher等[7]、Levi等[8]设计了基于回音壁模式的微盘激光器, 从此光学回音壁模式的谐振器开始在半导体领域的研究中取得突破.

在近些年的研究中, 回音壁微腔在光通信信号处理[9-10]、各类传感器[11-13]、腔光力学[14-17]等方向展现出巨大的应用潜力. 随着微纳加工技术和材料科学技术的不断发展和日益成熟, 微腔的形状越来越多样化, 如微球型[18]、微环型[19]、环芯型[20]、微柱型[21]、微盘型等微腔相继出现. 制备微腔的材料也越来越丰富, 目前常用的材料主要有二氧化硅[22]、铌酸锂[23]、氟化钙[24]以及各类聚合物[25]等. 这些由不同材料制成的形状不同的回音壁微腔在不同领域发挥了重要的作用.

亥姆霍兹腔结构简单, 一直以来在声学领域占有重要地位, 有着广泛的应用. 它可以用来设计消声器、扩声装置, 也可以用于乐器制造、建筑噪声控制等[26], 即使在近来声学超材料的研究中, 它也发挥了无可替代的重要的作用[27-28]. 鉴于亥姆霍兹腔在声学领域所表现出的独特优势, 人们也期待它能够在操控电磁波方面发挥独特作用. 在最近的研究工作中, 我们发现在该腔内会激发出一种特殊的磁对称偶极模式(Magnetic Symmetric Dipole Modes, MSDM), 基于这一模式, 单层亥姆霍兹腔阵列可以使斜入射的电磁波原路返回, 返回效率接近100%, 从而设计出高效且宽频带的回射器. 本文希望通过对腔内各回音壁模式的研究, 为理解腔内激发的如磁对称偶极模式等新电磁模式提供帮助. 同时,系统的研究也可以为亥姆霍兹腔的设计和优化, 及其在人工电磁材料中的应用提供理论基础. 下面的部分将在简要介绍我们采用的计算方法之后, 计算并给出理想电导体(Perfect Electric Conductor,PEC)构成的二维电磁亥姆霍兹腔内, 几种回音壁模式的激发波长, 并探讨入射方向与腔的开口方向的相对位置, 以及开口大小对回音壁模式的影响.

1 理论模型

本文中的二维亥姆霍兹腔由无限薄的理想电导体(PEC)围成, 为方便分析又不失一般性, 背景和腔内媒质都设为空气. 亥姆霍兹腔的几何结构如图2所示, 其中半径为r, 开口角宽度为θ, 所有腔全部向右开口, 且开口中心线与x轴重合, 所有腔的半径也固定为r= 60 mm不变, 入射角(入射方向与x轴的夹角)为θi, 图中红色箭头表示了入射光方向. 腔体内的回音壁模式可以用一个简单的模型来理解: 我们知道当光入射到理想导体表面上时会发生全反射, 当入射波进入亥姆霍兹腔中时, 入射电磁波便会在腔体的内表面连续发生全反射并绕腔体围成的圆周传播; 当圆周长度是波长的整数倍时, 便会在腔内形成稳定的驻波, 从而形成回音壁模式. 但精确计算并研究亥姆霍兹腔中的回音壁模式, 需要基于严格的方法来计算腔体的电磁散射. 亥姆霍兹腔与一般粒子的电磁散射问题相比, 难点在于它涉及混合边界问题, 即开口处与PEC腔体对应的边界条件不同, 这是它的散射问题数学上长期无法严格处理的主要原因. 在解决它的散射问题的过程中, Senior[29]通过积分方程法首先进行了数值计算, Bonbardt等[30]发展了近似的解析方法, 随后Shestopalov[31]和他的合作者用双级数方法研究了这个问题, 但仅对有限的亥姆霍兹腔结构适用. Ziolkowski等[32]将双级数问题变为Riemann-Hilbert问题, 发展了广义双级数方法, 可以用来计算任一亥姆霍兹腔的电磁散射, 并满足了对计算精度的任意需求. 为了系统精确地研究亥姆霍兹腔内的电磁模式, 本文采用了这种广义双级数方法(Generalized Dual Series Approach)[33]来计算电磁散射问题.

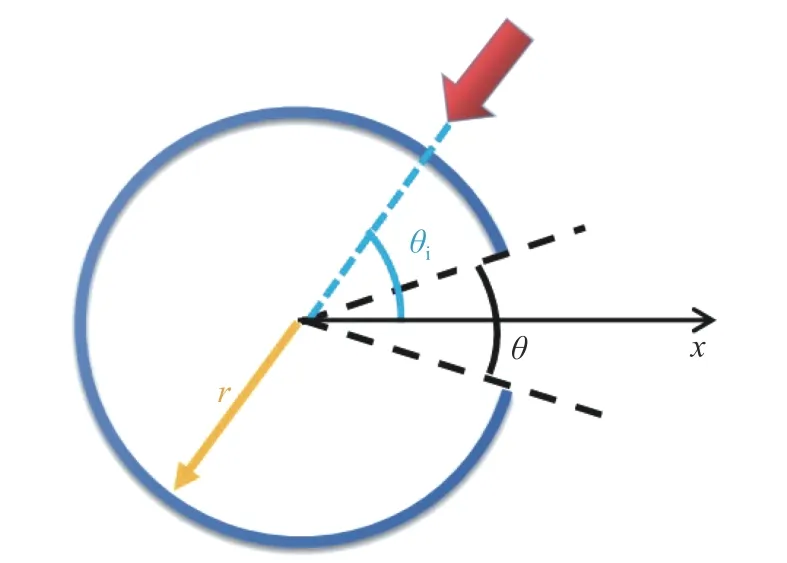
图2 半径为r, 腔体的开口大小为θ的亥姆霍兹腔的几何结构图, 入射角为 θi, 腔的开口中心线与x轴重合Fig. 2 Geometry of an EM Helmholtz cavity with radius r and angular width of the opening θ, θi is the angle ofincidence and the center line of the opening is the x axis

下面我们将针对横磁极化波(即电场沿腔轴方向极化的波)入射到二维亥姆霍兹腔的情形, 简要介绍广义双级数方法的计算过程. 整个论文中, 时间相关因子 eiωt省略未标出. 首先我们将入射平面波展开为

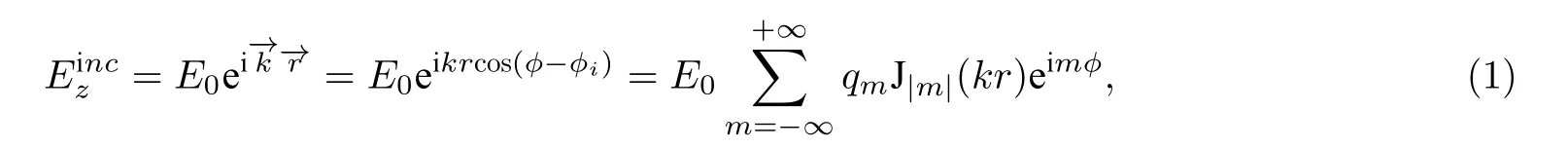
其中,qm=i|m|e−imϕi是入射场的展开系数. 散射场和内部场的展开式分别可以表示为

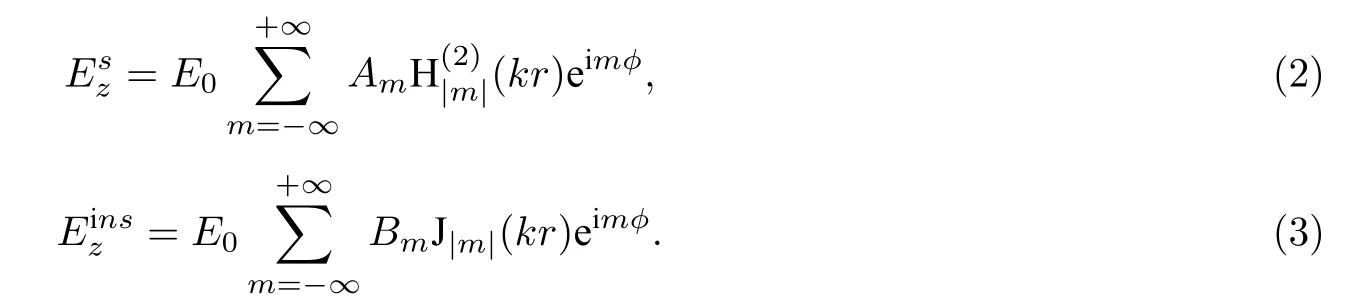
其中,Am和Bm分别是内部场和外部散射场的米氏散射系数.和 J|m|分别是第二类|m|阶汉克尔函数和|m|阶贝塞尔函数. 接下来, 分别利用金属上和开口处的两个电磁边界条件, 即金属上Etot,z=0和磁场强度的切向分量Htot,ϕ在开口处连续, 可以得到

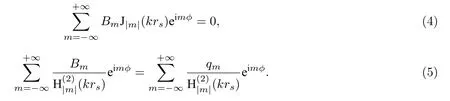
这样就得到了所谓的双级数问题. 变换后将该双级数问题转变为Riemann-Hilbert问题, 通过求解无限维线性方程组得到Am和Bm这两个系数. 一旦求解出米氏散射系数Am和Bm, 就可以严格计算散射场的空间分布, 分析其电磁散射的特点.

2 结果与讨论

2.1 回音壁模式与波长的关系

根据Mie散射理论, 不同极回音壁模式与不同的散射系数相关, 比如偶极回音壁模式对应B1, 四极回音壁模式对应B2, 以此类推. 我们首先考虑一个几何结构不变的亥姆霍兹腔, 研究它的各极回音壁模式与入射波长的关系. 设定亥姆霍兹腔开口角宽度θ= 14°, 图3表示了其前5个散射系数|Bm|与入射波长的关系. 从图3中可以看到, 不同m对应的散射系数的绝对量|Bm|有不同的峰值, 每个峰对应的波长下, 可以激发出一种回音壁模式. 另外, 在长波长区域, 不同|Bm|峰相对较分离, 也就是说, 长波长区域更容易激发出单个回音壁模式. 而在短波长区, 很窄的波长区域内有多个|Bm|峰同时出现, 这意味着短波长区域往往有多个回音壁模式混合出现. 虽然起主要作用的是该波长范围内的最强峰, 但此时腔内的模式较复杂. 长波长下的电磁模式对构造小尺寸的电磁元件非常重要, 而且可以清晰地展示出每个模式的特性, 因此本文主要研究长波长下几种重要的回音壁模式. 由于这些|Bm|峰很尖锐,相应地, 回音壁模式对波长的变化较为敏感. 物理上, 这种敏感与模式激发的条件相关, 由于腔内部的周长与波长满足特定条件才能形成驻波模式, 因此回音壁模式的激发只能在较小的波长范围内实现.

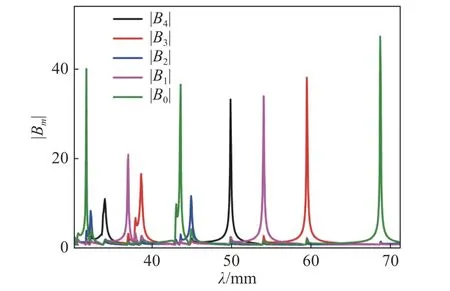
图3 半径r = 60 mm, 开口大小为 θ=14°的亥姆霍兹腔, 在入射角 θi=0° 时,前5个Mie散射系数的绝对量 |Bm| 与入射波长的关系Fig. 3 The absolute value of the first five Mie scattering coefficients,|Bm|, as a function of wavelength for a Helmholtz cavity with r = 60 mm and θ=14°, the angle of incidence isθi=0°

2.2 回音壁模式与腔体开口大小的关系

在得到特定回音壁模式对应的入射波长后, 接下来我们以偶极和六极回音壁模式为例, 研究开口大小对回音壁模式的影响. 由图3中入射波长与|Bm|值的关系图, 可以确定半径为60 mm, 开口角宽度为14°时, 这两种回音壁模式对应的激发波长. 在这两个波长附近, 我们计算了开口角宽度在6°到16°之间的亥姆霍兹腔中, 偶极和六极回音壁模式所对应的|Bm|值随波长的变化关系, 计算结果如图4a)和图4b)所示. 图4a)、图4b)中显示, 对于两种回音壁模式,|Bm|峰值高度随开口角宽度变化,峰值越高意味着激发的回音壁模式质量越高, 对应品质因子(Q值)越大, 因此不同开口大小的腔内回音壁模式的质量有差别. 从图中可以看到, 偶极和六极回音壁模式对应的最佳开口度分别为8°和10°. 图4c)和图4d)分别展示了这两种模式的Q值随开口角宽度变化的关系: 与图4a)和图4b)中Mie散射系数的变化一致,Q值也在开口角宽度分别为8°和10°时达到最大, 分别为542和593; 当腔体的开口大小偏离最佳值时,Q值很快变小, 即回音壁模式的质量下降明显. 物理上可以通过回音壁模式的原理来理解角宽度的影响: 开口过小可能造成入射波无法进入腔体, 自然无法形成强回音壁模式; 而开口过大时, 开口处缺少的腔壁会导致电磁波在腔体内无法完成严格的相位叠加, 从而也无法产生高质量的回音壁模式. 结果腔的开口大小对回音壁模式的激发有很大影响, 而且存在开口角宽度的最佳值, 太大或太小的角宽度都会影响模式的品质因子.

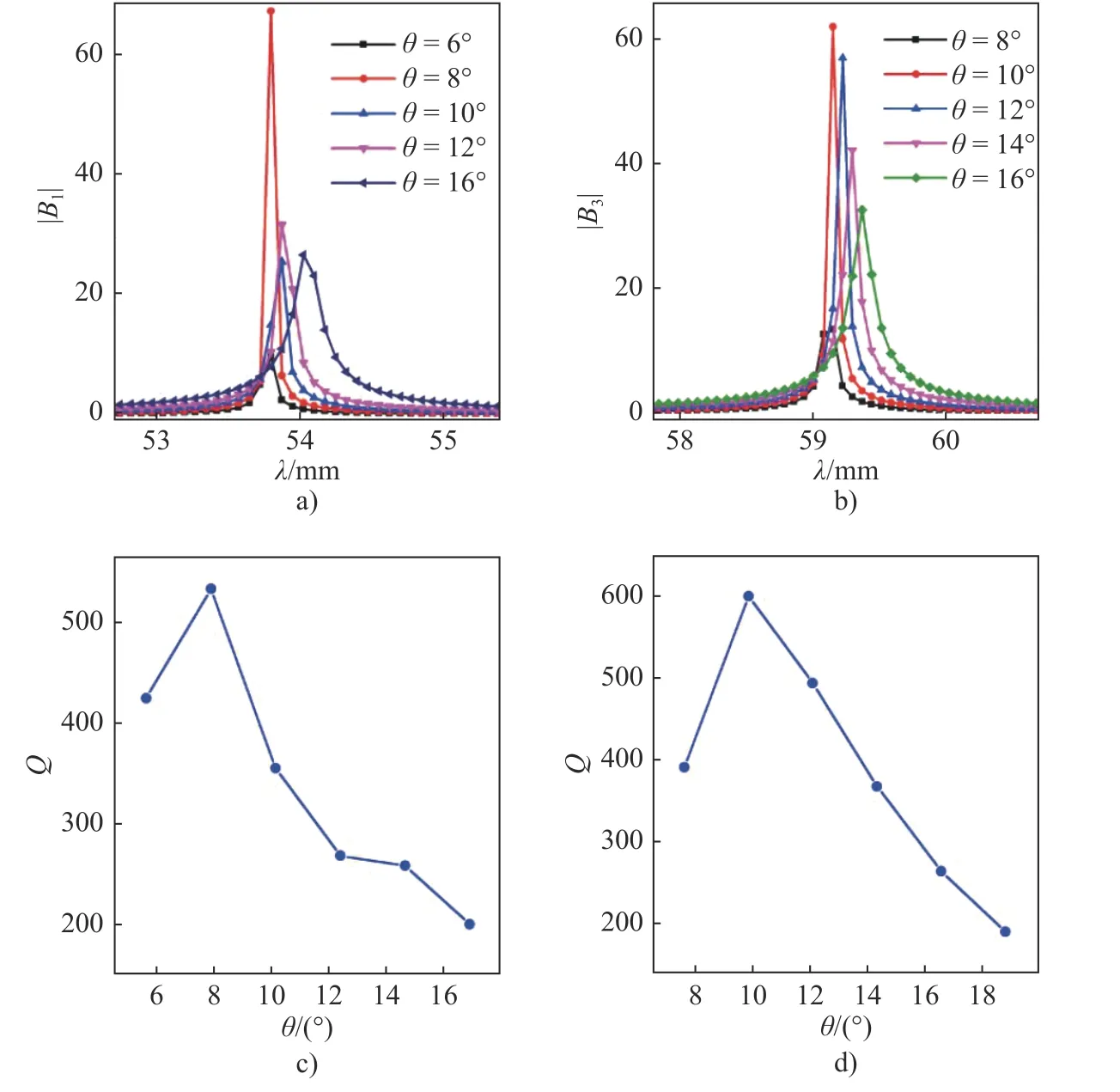
图4 半径 r=60 mm, 开口角宽度不同的亥姆霍兹腔, 在入射角 θi=0°时, a) Mie散射系数的绝对值 |B1| 和b) |B3| 随波长的变化; c) 偶极回音壁模式和d) 六极回音壁模式的Q值随腔的开口角宽度的变化Fig. 4 The absolute value of the Mie scattering coefficients a) and b) versus incident wavelength for Helmholtz cavities with the same radius r = 60 mm but differ ent angular widths of the opening; The quality factor, Q, of the dipole WGM c) and the hexapole WGM d) versus incident wavelength for Helmholtz cavities with the same radius r = 60 mm but different angular widths of the opening. The angle of incidence is θi=0°

由图4a)和图4c)可知, 开口角宽度为θ=8◦的亥姆霍兹腔, 利用λ=53.8 mm 的入射波可以激发得到最强偶极回音壁模式. 为了直观地对比开口大小对模式质量的影响, 在这一入射波长下, 图5a)和5c)分别计算并给出了腔体开口角宽度为20°和8°时, 散射电场的分布图. 图5e)中也计算了θ=8◦时, 磁场矢量在截面内的分布情况. 开口角宽度θ=10◦的亥姆霍兹腔,λ=59.2 mm 的入射波可以激发得到最强六极回音壁模式. 类似地, 图5b)和5d)分别计算并给出了开口角宽度为20°和10°时, 散射电场的分布图. 图5e)是θ=10◦时相应的磁场矢量分布情况. 所有图的计算中, 入射方向为θi=0◦. 从图5a)和图5c)、图5b)和图5d)中数值上的比较可以明显看出, 不同开口角宽度下偶极(六极)回音壁模式的质量有很大差异, 最强的模式被激发时, 柱内场最大值达8.0, 而θ=20◦时仅有1.5. 腔体的开口变大后, 回音壁模式的激发效果明显减弱, 这与图4中的|Bm|峰值和Q值的变化完全一致. 图5e)和图5f)中磁场的矢量分布图, 非常直观地体现了腔中激发回音壁模式时, 反射波相位匹配叠加, 相干相长的情形.

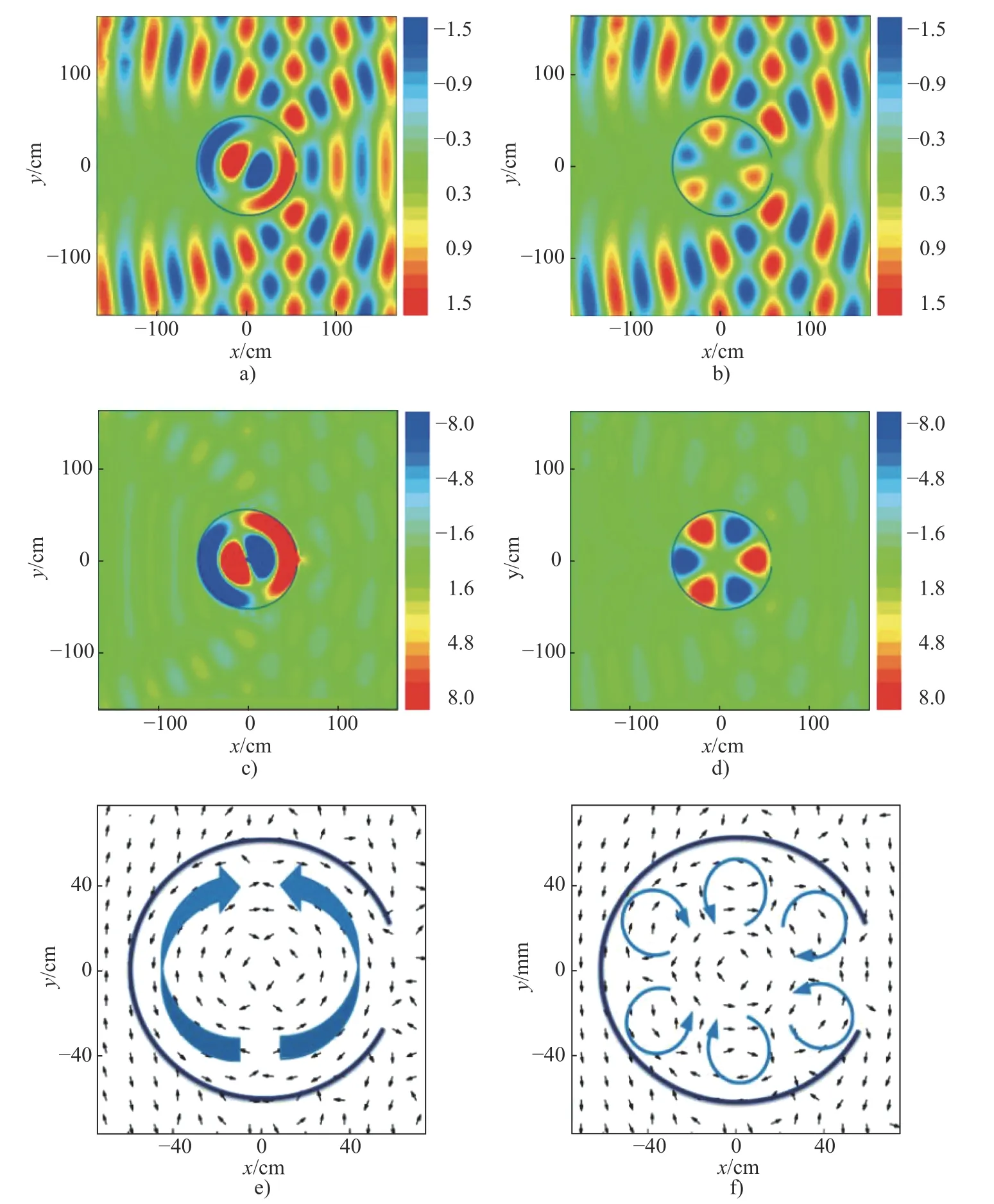
图5 半径 r=60 mm, 开口角宽度 θ=20° 的亥姆霍兹腔, 在波长a) λ=53.8 mm 和b) λ=59.2 mm 的波的入射下的电场分布图; c)、e)分别为半径 r=60 mm, 开口角宽度 θ=8°的亥姆霍兹腔, 在入射波长 λ=53.8 mm 的波的入射下的电场分布图和磁场矢量分布图; d)和f )分别为半径 r=60 mm, 开口角宽度 θ=10° 的亥姆霍兹腔, 在入射波长 λ=59.2mm的波的入射下的电场分布图和磁场矢量分布图. 入射角均为θi=0°Fig. 5 The E field distribution when an EM wave with a) λ=53.8 mm and b) λ=59.2 mm strikes a Helmholtz cavity with radius r = 60 mm and angle width of the opening θ=20° ; c) The E field distribution and e) the magnetic field vector distribution when an EM wave with λ=53.8 mm strikes a Helmholtz cavity with radius r = 60 mm and angle width of the opening θ=8° ; d) The E field distribution f) and the magnetic field vector distribution when an EM wave with λ=59.2 mm strikes a Helmholtz cavity with radius r = 60 mm and angle width of the opening θ=10°. The angle of incidence isθi=0°

2.3 回音壁模式与入射方向的关系

接下来我们改变入射角θi, 研究入射波方向对回音壁模式激发的影响. 为了方便比较和深入探讨,我们仍然选择偶极和六极两种回音壁模式进行研究. 选取图5给出的入射波长与腔体开口大小的最优值, 然后只改变入射角θi, 分别计算这两种回音壁模式在入射角为0°到90°的范围内|Bm|值的大小,结果如图6a)和图6b)所示. 从图6a)和图6b)中|Bm|峰值的变化可以看出, 当入射角度在0°到30°之间变化时,|Bm|峰值全部处于比较高的状态. 这意味着在这个入射角范围内, 腔内始终可以激发起高强度的回音壁模式. 我们计算了入射角为15°和25°时, 亥姆霍兹腔中六极回音壁模式的散射电场分布图, 分别如图6c)、图6d)所示. 对比图6c)和图6d)可以看出, 只改变入射方向, 腔中电磁模式的相位分布是一致的, 回音壁模式的强度也几乎没有发生改变, 这与图6b)中|Bm|峰值所反应的模式强弱一致. 因此, 我们认为当入射角在0°到30°之间变化时, 腔内总是可以激发起高强度的回音壁模式. 但随着入射角度θi的继续增加,|Bm|峰值的高度开始明显下降, 这意味着入射角度大于30°时, 所激发的回音壁模式在强度上将显著降低. 因此, 与对开口角宽度的变化非常敏感相比, 入射角有一个较宽的变化范围, 在这一范围内腔中都可以激发出高强度的回音壁模式.

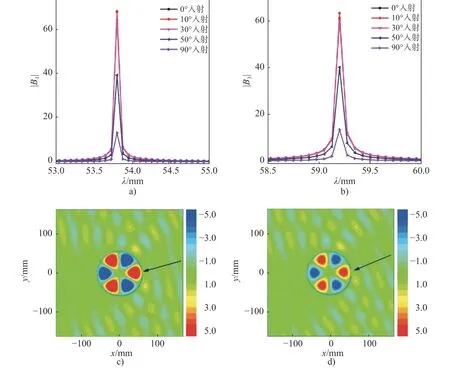
图6 a)半径 r=60 mm, 开口角宽度 θ=8°的亥姆霍兹腔, 在不同入射角下, Mie散射系数的绝对量 |B1| 随波长的变化关系; b)半径 r=60 mm, 开口角宽度 θ=10° 的亥姆霍兹腔, 在不同入射角下, Mie散射系数的绝对量|B3|随波长的变化关系; 半径 r=60 mm, 开口角宽度 θ=10° 的亥姆霍兹腔, 在入射波长 λ=59.2 mm 、入射角分别为c) 15°和d) 25°时, 电场的分布图Fig. 6 a) The absolute value of the Mie scattering coefficients,|B1|, versus incident wavelength for Helmholtz cavities with radius r = 60 mm and angular width of the opening θ=8° at different incident angle; b) The absolute value of the Mie scattering coefficients,|B3|, versus incident wavelength for Helmholtz cavities with radius r =60 mm and angular width of the opening θ=10° at different incident angle; The E field distribution when an EM wave with λ=59.2 mm strikes a Helmholtz cavity with radius r = 60 mm and angle width of theopening θ=10° at an angle of incidence c) θi=15° and d)θi=25°

2.4 仿真结果

在上面的模拟中, 我们假设亥姆霍兹腔的PEC壁是无限薄的. 但是, 在实际设计中必须考虑PEC壁的厚度. 我们使用Lumerical FDTD模拟了壁厚为0.2 mm的亥姆霍兹腔中的回音壁模式, 腔的其他参量与图5中相同, 结果如图7a)、图7b)所示. 模拟结果表明在实际的有壁厚的亥姆霍兹腔中,同样的回音壁模式仍然可以被激发起来. 因此这一理论研究所展示的各种回音壁模式在实际结构中都真实存在.

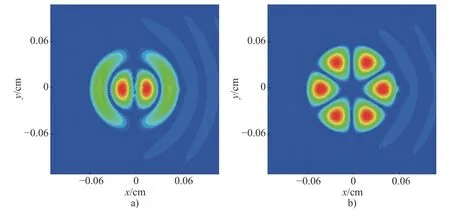
图7 a) 半径 r=60 mm, 壁厚 t=0.2 mm, 开口角宽度 θ=8°的亥姆霍兹腔, 在入射波长 λ=53.8 mm 时的电场分布图; b) 开口角宽度变为 θ=10°, 在入射波长 λ=59.2 mm 时的电场分布图. 入射角均为θi=0°Fig. 7 a) The E field distribution for the Helmholtz cavity with radius r = 60 mm, wall thickness t=0.2 mm and angular width of the opening θ=8° at λ=53.8 mm ; b) The E field distribution for the Helmholtz cavity with radius r = 60 mm, wall thickness t=0.2 mm and angular width of the opening θ=10° at λ=59.2 mm.The angle of incidence isθi=0°

以上是在横磁极化波, 即电场沿腔轴方向极化时, 腔内模式的激发情况. 下面我们计算了横电极化波, 即电场沿腔轴方向极化时, 腔内偶极和六极模式的激发情况, 如图8a)和图8b)所示. 由于电与磁的对称性, 横电极化下也可以激发起各种回音壁模式, 且所激发模式的质量和波长、开口大小的关系与横磁情况基本类似, 我们不做进一步的深入分析.

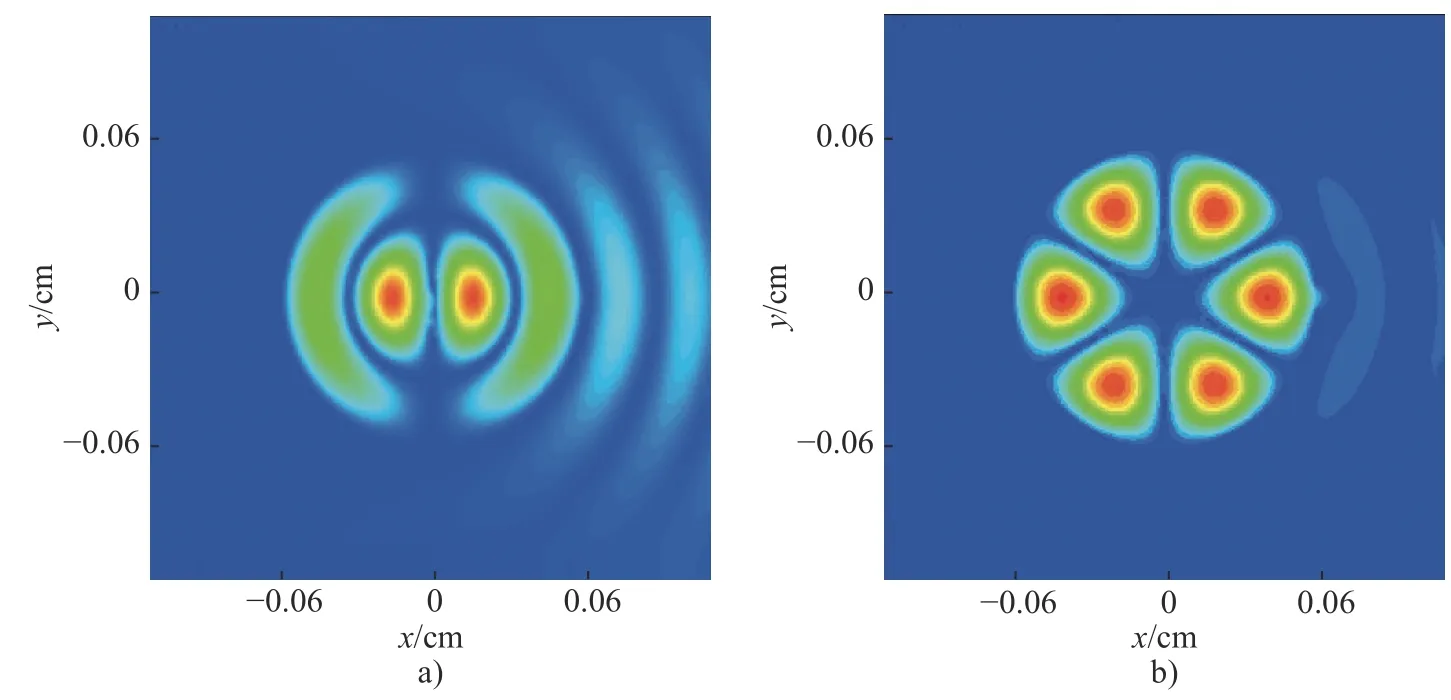
图8 当入射波为横电极化波时, 半径 r=60 mm: a) 开口角宽度 θ=8°的亥姆霍兹腔, 在入射波长λ=53.5 mm时的磁场分布图; b) 开口角宽度变为 θ=10°, 在入射波长 λ=58.8 mm 时的磁场分布图. 入射角均为θi=0°Fig. 8 The H field distribution for the Helmholtz cavity with radius r = 60 mm and angular width of the opening θ=8°for the transverse-magnetic polarized wave with λ=53.5 mm ; b) The H field distribution for the Helmholtz cavity with radius r = 60 mm and angular width of the opening θ=10° at λ=58.8 mm.The angle of incidence isθi=0°

3 结 论

本文研究了完美电导体(PEC)围成的二维电磁亥姆霍兹腔中, 回音壁模式与入射波长、腔的几何结构之间的关系. 基于严格的双级数方法计算出腔的Mie散射系数|Bm|, 在其峰值附近激发各种回音壁模式, 并通过|Bm|峰值或品质因子的变化, 得到了固定大小的亥姆霍兹腔中, 激发高质量回音壁模式所需的波长与开口角宽度. 同时分析发现, 回音壁模式对入射波长和腔体开口大小的改变非常敏感,但对入射角没有严格的限制, 入射角在一个较宽范围内变化, 腔中都可以激发高质量的回音壁模式,这是亥姆霍兹腔在人工电磁材料应用中的一个重要优势.