函数拟合实现语音演唱

王咿卜,李建文

（陕西科技大学 电子信息与人工智能学院, 西安 710021）

0 引 言

语音语调作为人类交流的主要特点之一, 是情感表达最不可忽视的一部分, 也是人类区别于机器语音最显著的特征[1]. 人工智能的发展, 带来的是全新的机器时代, 精确度更高的算法相应而生, 但在要求准确度和语音合成清晰度的同时, 不可忽视的还有机器语音区别于人类语音的一点—语调. 只有将语音合成的准确度和情感度结合起来, 才能真正达到智能化语音, 使机器语言更加贴合人类的日常交流, 这对语音合成的实现提出了语调可控的要求, 其中, 语音演唱复杂度更高, 如果能实现语音演唱, 会使得机器模仿人类日常交流更加简单. 语调是区别不同人发音特征最重要的参数之一, 语调的拟合有助于语音识别准确度的提高. 语音信号占据人类信息交流的70%左右, 最容易获取且最能体现人类在不同场景的心理状态. 研究显示, 语音语调的变化特征在抑郁症患者和正常人之间有着明显的区别[2], 因此, 从数学角度出发, 结合对语音参数的调整实现语音合成, 在人工智能、医学方面都具有参考价值.

徐晨煜[3]基于统计机器学习的端到端的方法实现语音合成, 以传统的文本到语音(Text To Speech, TTS)为基础, 采用一种端到端的合成模型将整个过程统一为一个单一的过程, 利用支持向量回归、简单神经网络以及具有注意力模型的Seq-2-Seq算法, 实现文本到语音的转换. 王永鑫等[4]采用基于HMM方法实现带声调控制的语音合成, 通过研究陈述语句和疑问语句的基调变化特点, 对其进行归一化, 利用HMM语音合成系统的控制机制, 实现了对疑问句语调到陈述句语调的转换. 徐晨煜的研究在一定程度上简化了语音合成的复杂过程, 但忽略了不同人之间的发音特点, 将人类之间情感的区别单一化, 机器音更为明显. 王永鑫等的研究考虑了语调的重要意义, 结合语句参数的变化特征,实现了陈述句和疑问句之间的转换, 但可变语调仅仅局限于陈述语句和疑问句, 对于多种语句类型的转化要求难以实现. 本文研究从语音的基频和共振峰两个参数出发, 通过研究不同情况发音者的基频变化值, 调整拟合的基频曲线, 实现了对不同情境下说话人语调的变化; 同时调整基频曲线参数、发音时长也可以实现语音演唱的效果, 并且通过调整基音频率值还可以达到对男士、女士、儿童等发音者的变化. 本文通过对函数拟合实现语音合成及演唱方法的研究, 以期在语音演唱、语音合成、语音识别、医学领域等方面提供参考.

1 语音参数

1.1 语音数字模型

声音的产生, 主要是人类的发音器官受到大脑控制, 这些发音器官主要有肺、气管、喉以及声道,图1所示为发音器官示意图[5-6].

由图1可知, 肺承担着人体血液和气体之间的交换, 通过肺将二氧化碳排除并吸进氧气, 并将空气压缩传递给发音器官, 即呼吸功能. 气管主要将声音由肺部传递到喉部. 喉部含有发音的重要器官—声带[5]. 声音之所以产生, 主要是气流进入喉部, 产生声带的振动, 而这种振动的强弱、大小则导致声音种类的不同. 从声门到嘴唇之间所有的发音器官统称为声道, 包括咽头、口腔和鼻腔. 口腔包括唇和舌头. 口腔中所有器官共同协作使得通过的气流受到阻碍产生震颤, 导致不同声音的产生, 声道与咽腔、鼻腔一同充当发音的共鸣器. 声道是一种非均匀截面的声管, 截面面积取决于唇、舌、腭和小舌的位置和形状, 这种非均匀截面随时间不断变化[5]. 通过对发音器官的介绍, 可以构造出发声的数字模型, 图2所示为发音数字模型[5].

从图2可知, 声音种类的不同正是因为这些器官在根据大脑刺激产生不同的协作[5], 首先气流进入肺部, 产生有规则的信号, 即直流气流, 直流气流经过声带的振动产生交流气流, 再通过声道得到速度波, 最终经过嘴唇作为辐射源产生声压波传入人耳[7].

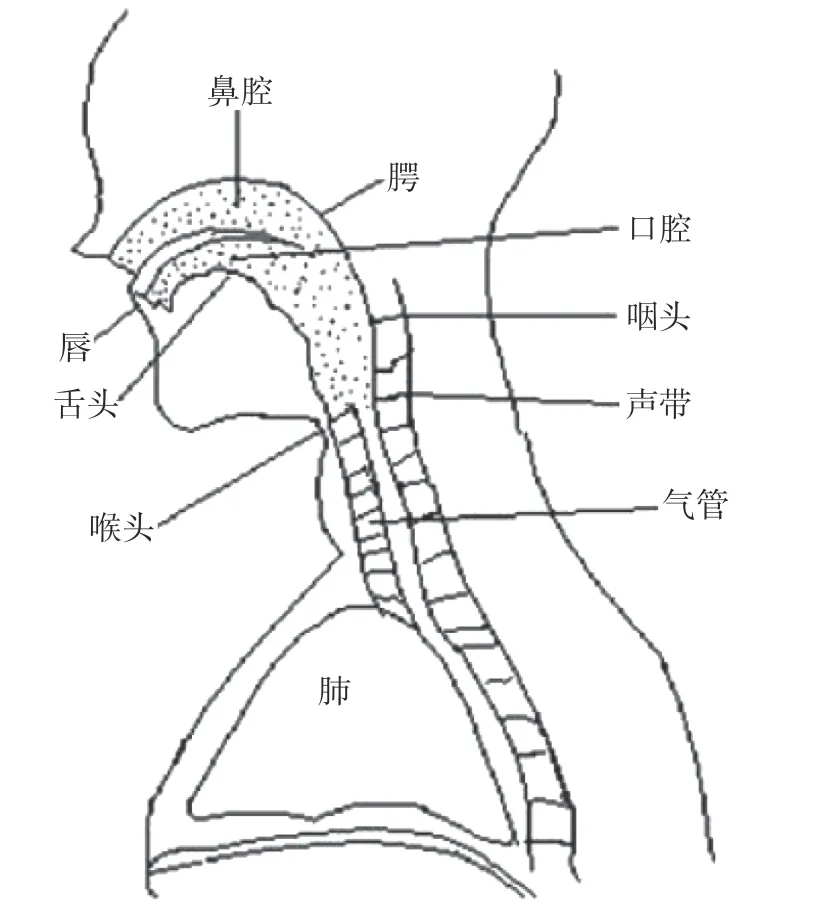
图1 发音器官示意图Fig. 1 Schematic diagram of speech organs

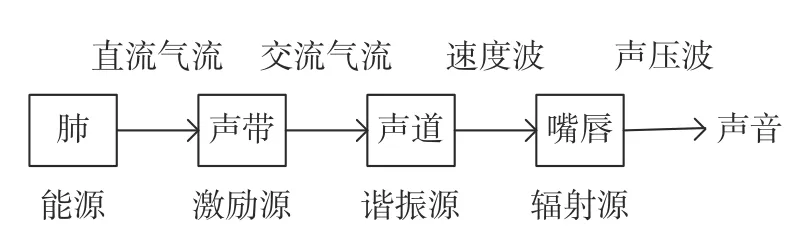
图2 发音的数字模型Fig. 2 Numerical model of pronunciation

1.2 声音参数及要素

声波信号产生于声带的周期性振动, 主要由基音与泛音组成, 声波信号中含有最低频率值的音波称为基音. 除此之外的音波都称为泛音, 其频率为基频的整倍数, 称为共振峰频率. 采用Adobe Audition软件对拼音一声“a”的语谱图进行显示, 如图3所示. 由图3可知, 最低高亮线所在位置对应的频率就是基音频率值, 其余高亮线条所在位置对应的频率为谐波频率值, 即共振峰频率值.

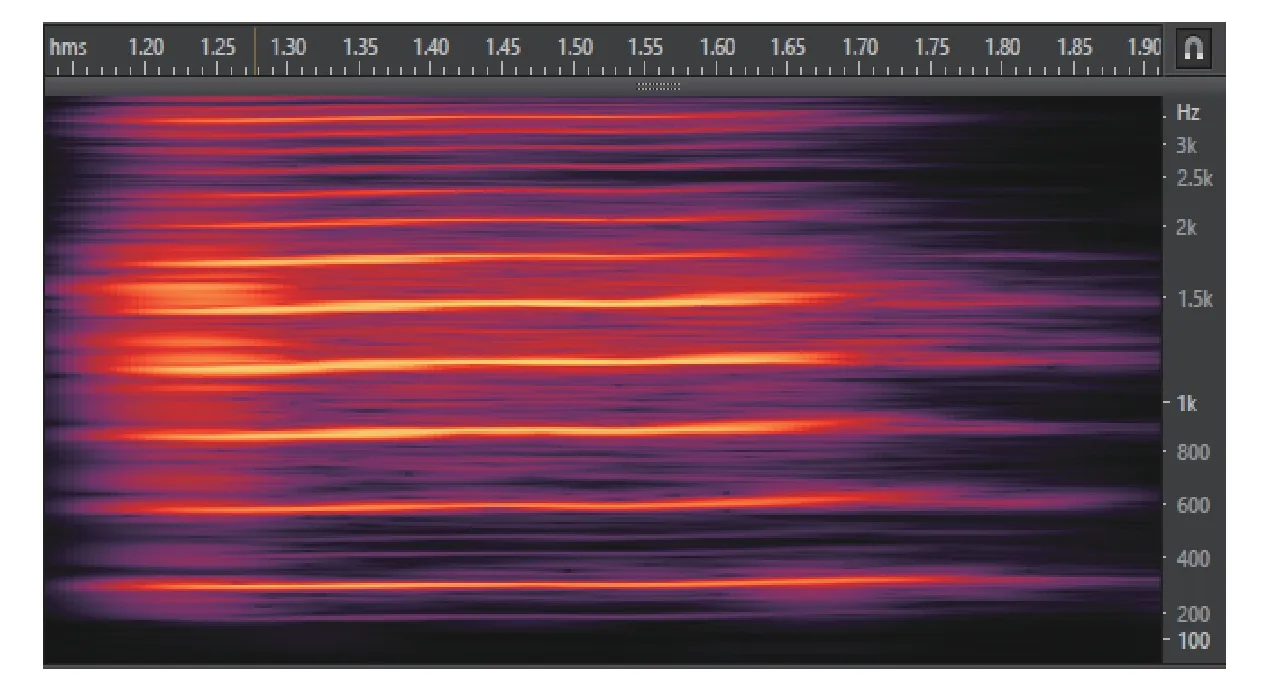
图3 一声“a”的语谱图Fig. 3 The spectrogram of “a”

声音主要有音调、音色、响度这3要素, 这些要素的不同组合构成不同状态下不同人的发音结果.声带有规律的振动存在周期性, 周期的倒数为频率, 其大小决定声音的高低, 频率增加一倍, 音乐上称“提高一个八度”, 这种高低即音调, 物体振动变化越快, 频率越高, 音调越高[8], 而声调的变化是相对的、滑动的, 用音阶来模拟. 声带的振动会产生两种类型的波, 一部分波周期一致, 另一部分波周期存在微小偏差, 周期不同导致这些波的频率不同, 此类波称为谐波. 谐波的频率是基频的整倍数, 发出的音在音乐中称为泛音, 当所有泛音整合在一起就会发出不同类型的音色, 音色由声音的波形决定, 根据声音的音色可以分辨不同人和不同乐器发出的声音[9]. 响度指声音的强弱程度, 单位是分贝(dB),与语谱图中基频曲线及共振峰对应曲线处的声强有关, 表现在语谱图上是图中高亮线段的明暗程度:越亮, 则分贝值越大, 发出的声波越明显; 越暗, 则相反. 声强即分贝值(ddB)与声音信号的幅度(时刻i位置的幅度为Ai)成正比[10-11], 声音信号幅度与声强之间的关系为

综上, 声音要素变量与物理变量之间的关系描述见表1.

表1 声音要素与物理变量关系Tab. 1 The relationship between sound elements and physical variables

1.3 声音分类

声音分为噪音和乐音, 噪音是发音物体产生多种无规律的周期和幅度而形成的声波, 即不同声波含有无规则的振动频率和响度, 语音波形不定[12]. 乐音是声带周期性振动产生的, 声波频率呈基频F0的整数倍增加, 为F1,F2,F3,···, 响度参数值较为统一, 差距较小, 有一定的语音波形.

一般来说,F1、F2决定了音型,F3及其以上共振峰则影响着个人的声音特征及音色[13]. 乐音又分为浊音、清音和鼻音. 浊音有声带振动的参与, 是气流受到阻碍的同时声门发生了闭合, 并且声带微颤而产生, 如/p/、/t/、/k/等. 清音无声带振动的参与, 仅仅是由于气流收到阻力而产生[14], 如/b/、/d/、/ɡ/等. 鼻音是由于肺部气流在传递上升过程中声带发生闭合, 声带微颤的同时发出的声音, 这种声音随着气流送入鼻腔产生, 例如/l/、/m/、/n/等. 由于音调由物体振动频率决定, 因此在歌曲的演唱过程中, 浊音的乐音性强于清音, 鼻音的乐音性要强于浊音.

2 语调拟合

2.1 基频提取

基音周期是指人们发出韵母的浊辅音时, 声带发生一次开启与闭合的时间[7]. 基音周期倒数为基音频率(简称“基频”). 基音周期描述了图2语音数字模型中发音激励源的重要特征, 是研究语音信号最重要的参数之一. 基音频率的波形变化曲线(基频曲线)称为声调[11].

令离散的语音信号为x(n), 由图2得语音信号是由声门脉冲激励u(n)经声道响应v(n) 滤波而得, 即

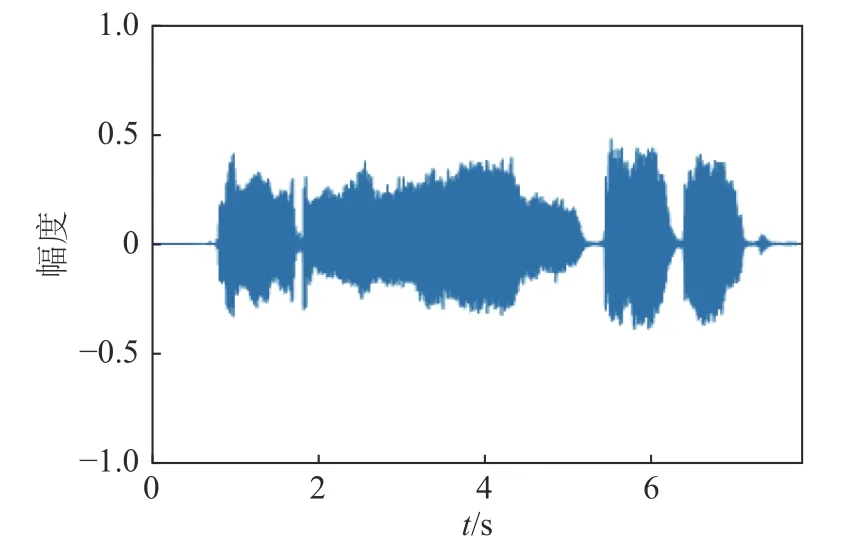
图4 语音信号波形Fig. 4 Voice signal waveform

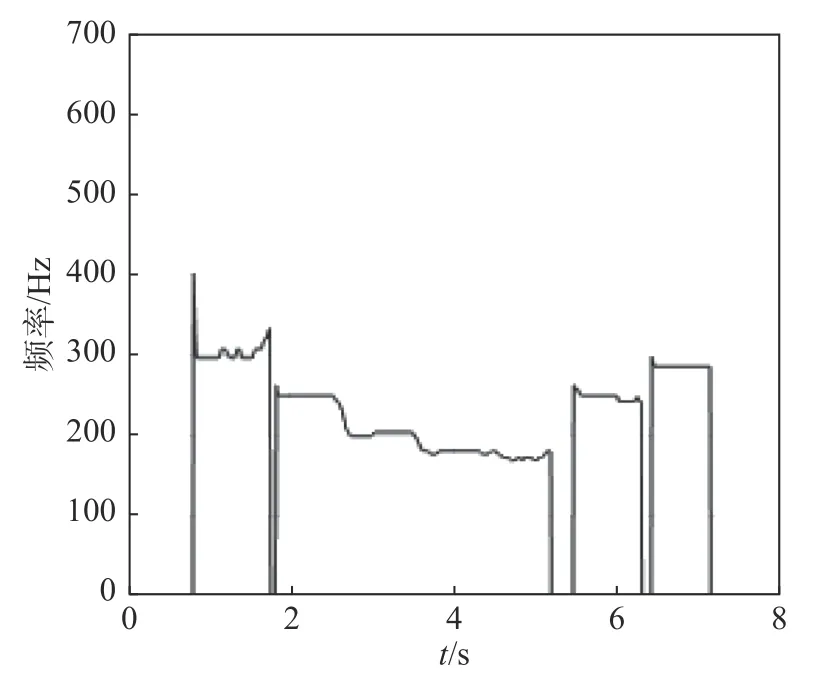
图5 语调基频曲线Fig. 5 Tone pitch curve

对于乐器来讲, 每相邻两个半音, 高音频率是低音频率的2的次方倍, 例如, 国际标准音“a”的频率为440 Hz, 比它高半音(降b)的频率为 440×=466.13 Hz[17]. 从图5中可得, 实际情况下, 对于含有音阶变化的起音“a”, 每个相邻音阶频率变化值从高音到低音依次为50 Hz、50 Hz、25 Hz左右,降低的值呈倍数性衰减. 两两音阶变换位置存在类似梯形的过渡, 由一段音阶递减或递增到另一音阶.同一音阶处曲线起伏较小, 基本趋于水平状态.

2.2 共振峰提取

语音信号可以看作是一个数学模型模型的输出, 图6所示为其等效模型.

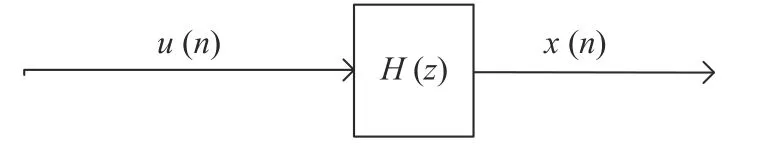
图6 语音信号数学模型Fig. 6 Mathematical model of a speech signal

图6中u(n)为模型输入, 即脉冲序列,x(n)为输出的语音信号, 而模型的传递函数为H(z), 其有理式形式为

由于H(z) 是稳定且具有最小相位的系统, 因此可化为

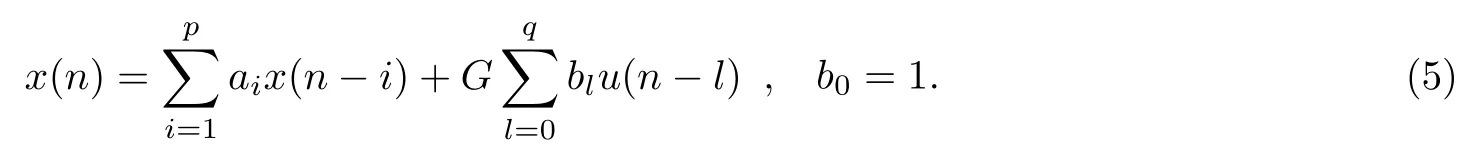
由式(5)得, 模型的输出是模型当前的输入、过去的输入和输出之间的线性组合. 因此, 语音信号当前的输出值可以通过当前的输入与过去的语音信号值来计算. 式(5)中, 若b1,b2,···,bq均为0, 则式(5)可变为

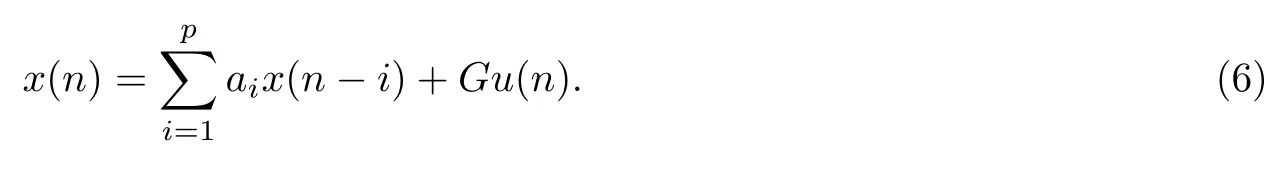
当声道传递函数为全极点模型时, 有

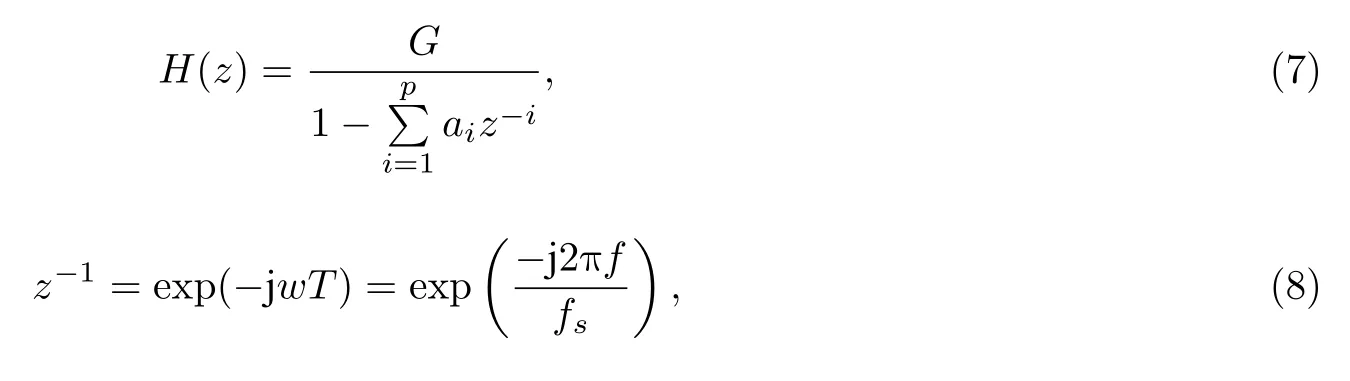
其中, j是虚数单位, j2= –1.

将式(8)代入式(7), 并取功率谱模值, 用p(f) 表示, 有

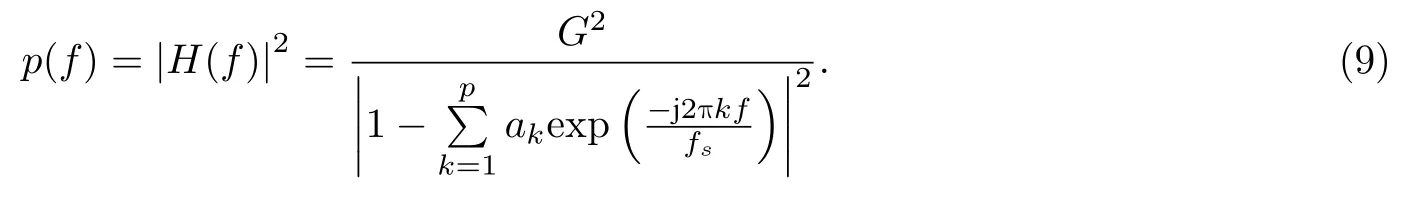
由式(9)可得, 当求共振峰频率值时, 可先利用FFT对任意频率求其功率谱幅值响应, 再从幅值响应中找到共振峰的信息[7,18].

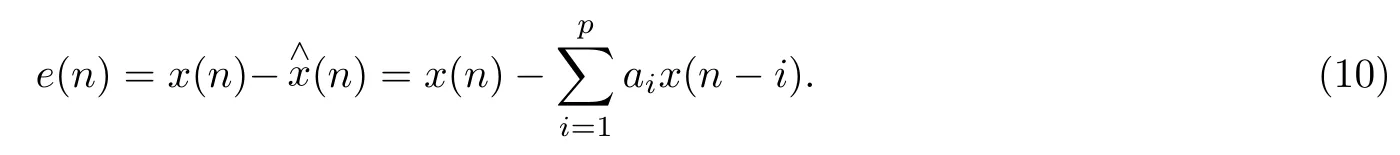
由式(10)得,x(n)为e(n)的输入, 也是传递函数的输出. 利用A(z) 的多项式系数分解能够准确的确定语音信号共振峰的中心频率与带宽. 设为任意复根值, 则其共轭值也是一个根. 设zi对应的共振峰频率为Fi, 3 dB带宽为Bi, 衰减指数为σ, 拉普拉斯变换和Z变换转换关系为Z=esT(s为信号x(t)经过拉普拉斯变换后得到的极点,s=−σ±jω), 得到Z变换后的极点Z1=e−σT+jωT=rejω和Z2=re−jw, 经过对比得θi=ωi=ω0T, 其中ω0为信号原频率, 由于σ=2πB/2=πB,ωi=2πfi, 则Fi与Bi、zi之间关系为

由于ri=r=e−σT=e−πBT, 则

由式(11)、式(12)得

通过LPC求根法对共振峰估算, 得到语音包络线, 如图7所示. 图7中功率谱曲线上画出的点画线即对应的共振峰频率值.

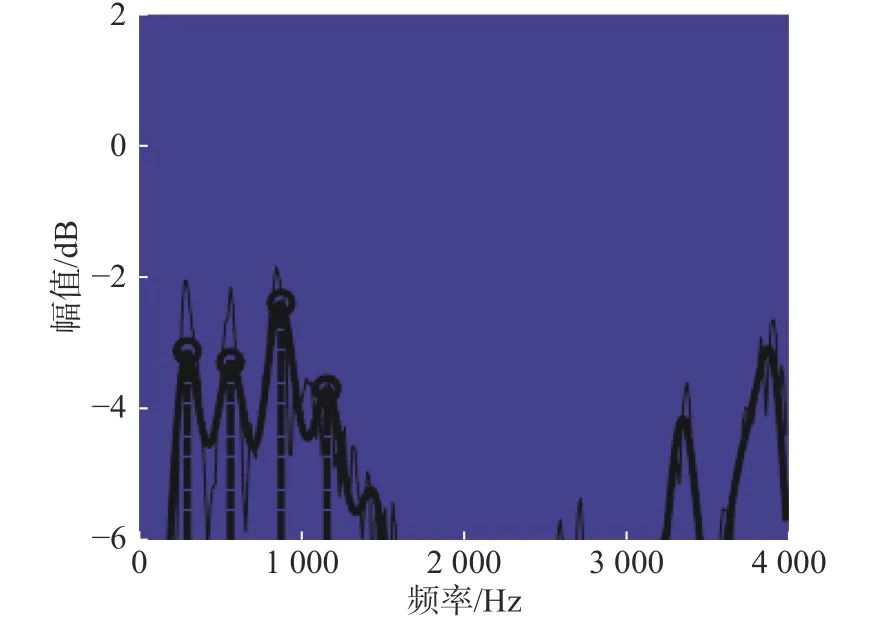
图7 语音包络线Fig. 7 Voice envelope

3 语调分析

声调随着基频的变化而变化, 这种变化结果合称语调. 一般来说, 女性的基音频率是男性基音频率的两倍, 男性范围约为50 Hz ～ 250 Hz, 儿童和女性约为100 Hz ～ 500 Hz[19]. 发音者类型、发音状态、发音语句类型都在一定程度上影响着基频[20]. 在语音合成过程中, 语句的表达状态不同, 基音频率也存在明显的差异, 例如陈述语句和疑问语句的基音频率在句末处差别很大, 陈述语句的基音曲线走势整体平缓, 基本保持水平状态, 到句末位置处稍微下降, 而对于疑问句, 基频曲线整体走势上扬, 基频值在句末处存在部分音节的基频明显增加, 当存在语气助词(如“吗”), 末尾音节基频值变化程度更高[21]. 语音发出者在不同情景下的发音状态也在一定程度上影响着基频曲线, 例如, 当人处于生气状态下, 基频曲线变化程度快, 声强较高, 当人处于愉悦状态下, 基频曲线变化平缓, 声强相对于日常来讲相对适中[22].

由于语音合成有两个重要参数, 分别是基频和共振峰的频率值, 基频曲线受现实情况的影响较大,而共振峰的频率值是基频曲线对应频率值的整倍数, 同样受到影响. 因此, 在进行带语调的语音合成及语音演唱的合成过程中, 要充分考虑不同人、不同状态、不同语句对基频曲线的影响, 以达到合成结果与实际情况切合.

4 拟合函数

4.1 拟合函数

采用最小二乘法原理对基频曲线进行拟合, 由于拟合的曲线方程y为

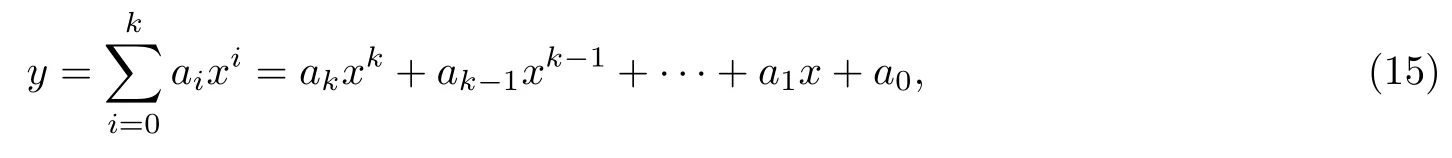
其中,ai为拟合系数,x为时间变量. 为使得曲线尽可能多地反映所给数据点的变化趋势, 要求产生的误差越小越好, 选择均方误差Q来表示误差大小, 已知基频曲线共有m个点[23], 某一点数据为(xi,yi),i=1,2,···,m, 则均方误差为

误差最小, 即求Q的极小值, 可以采用求导来解出ak,ak−1,···,a0, 即

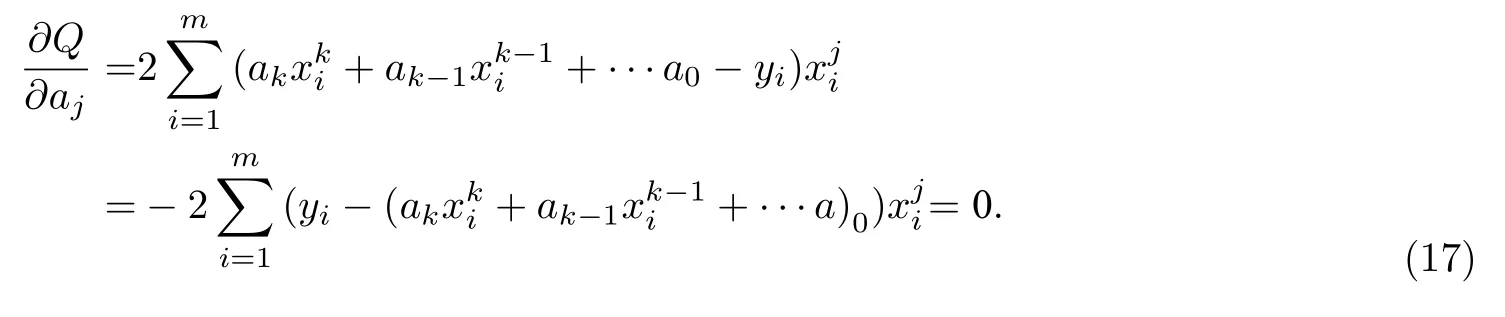
将式(17)整理后得

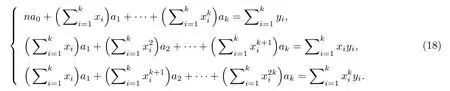
将式(18)表示为矩阵, 即

4.2 拟合函数阶数

已知, 当n的阶数越高, 拟合曲线占据实际点越多, 但在基频曲线提取过程中, 不可避免地产生一些“野点”, 导致产生过拟合, 因此n值选择是否恰当, 对语音合成结果的正确与否至关重要. 对于图4含有音阶变化的语音“a”, 实验采用其中前4个下降的音阶为例, 通过求解矩阵方程, 最终得到拟合参数值, 判断函数次数. 表2为对第一段音阶(不含过渡音阶曲线)不同阶数的拟合结果.

表2 拟合函数不同阶数对比Tab. 2 Comparison of different orders of fitting functions

确定系数表示拟合的函数变量对原始函数数据的拟合效果, 确定系数越接近1, 拟合结果越好. 从上表可得, 当阶数n< 3时, 对非线性曲线的拟合结果较差, 当n= 3拟合效果较好, 当n> 3, 确定系数虽然也在增加, 但程度减慢且系数值过于复杂. 为了保证拟合效果且避免过拟合, 实验采用阶数n为3进行拟合.

5 实验及结果

5.1 基频曲线拟合步骤

由于语音合成过程中, 基频和共振峰频率决定了整个合成结果语调的类型, 而共振峰频率为基音频率的整倍数[7], 因此首先对语调的基频进行曲线拟合, 图8所示为拟合过程.

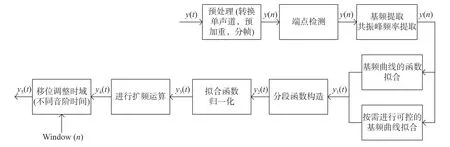
图8 基频曲线拟合步骤Fig. 8 Fitting steps for a fundamental frequency curve

从流程图中得, 基频曲线拟合过程分为以下几步.

(1)首先对语音y(t) 进行预处理, 将语音双声道模型转换成单声道以便处理. 对单声道音频进行分帧处理, 将连续信号y(t)变为离散信号y(n), 便于获取每帧信号值.

(2)对于语音信息较多的音频, 需要进行端点检测, 即将一段语音信号的每一个语音单元(每个字音)进行检测并区分.

(3)采用倒谱法提取基音频率, 得到语音基频曲线, 采用LPC法进行共振峰频率提取.

(4)若合成原始语音, 则采用高次多项式进行基频曲线的拟合, 若实现语音演唱, 则按照演唱需要利用分段函数将不同音阶的基频曲线拟合出来[24], 最终输出拟合函数y2(t), 即

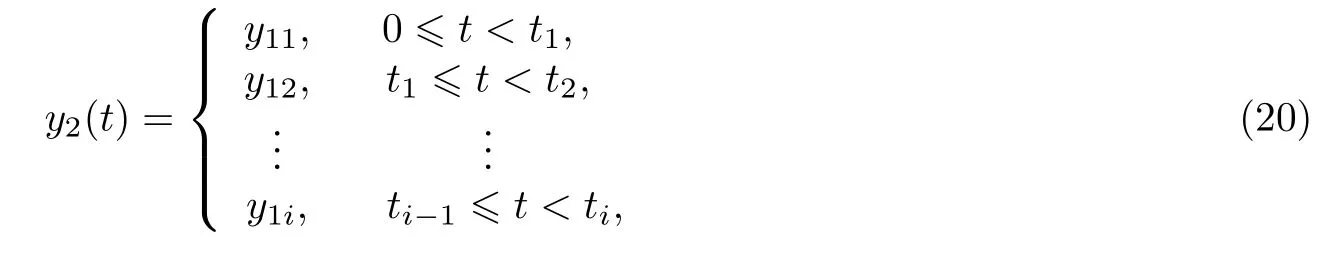
(5)为合成基频大小可以控制且语调确定的语音, 需要将拟合函数归一化, 即

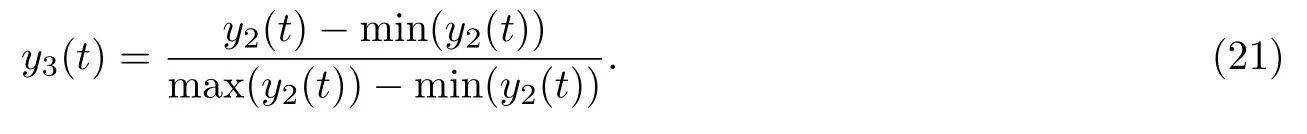
(6)得到的归一化函数加指定基频值F0, 得到最终语音的基频函数曲线

(7)对不同音阶时域进行整理, 通过调整拟合函数时间(加减t0),y5(t)=y4(t±t0) 最终实现语音演唱功能.

5.2 Pitch模型

由于实现语音演唱需要改变语音的音阶, 且在不同音阶处存在过渡音阶曲线, 因此采用分段函数来表示含有音阶变化的基频曲线. 实验采用3阶多项式函数, 对图5中前四段声调变换的基频曲线及过渡音阶曲线分别进行拟合, 由于语音音阶变化存在频率变化, 其频率随前后音阶的改变而调整, 因此需要对拟合的音阶基频曲线进行归一化, 最终得到的第一段音阶曲线和过渡音阶基频曲线的拟合函数分别为

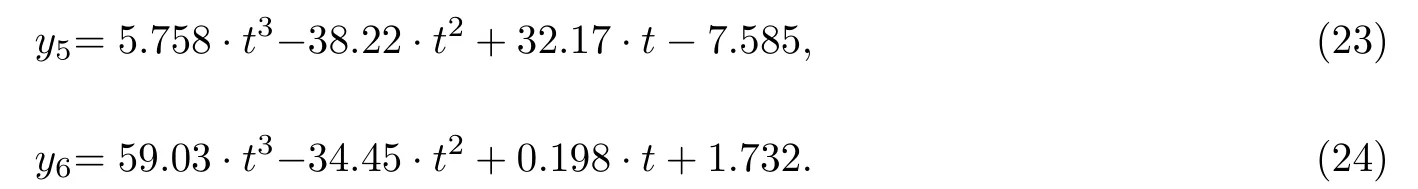
经过基频检测, 在图5中前4段音阶中, 每段相邻音阶的基频存在小范围波动, 相邻音阶基频曲线整体上移, 初始基频分别313 Hz、275.8 Hz、238.6 Hz、223.1 Hz. 对于过渡音阶, 其基频变化幅度分别为50 Hz、50 Hz、25 Hz、12.5 Hz(取平均变化). 为实现每段基频曲线的过渡, 需要对式(23)进行移位, 对式(24)进行扩频运算. 令每段音阶发音时长为0.7 s, 音阶过渡时长为0.2 s, 采样率fs为8 000 Hz,拟合的第i段音阶基频曲线y1i和音阶过渡基频曲线yni(i=1,2,3,4), 其对应公式分别为

对于音阶过渡基频曲线, 扩频运算仅仅能保证音阶基频变化幅度的正确性, 但在每一个分段曲线的连接处无法实现前后音阶的衔接, 因此还需要对式(26)进行纵轴移位. 实际情况下, 第i段音阶过渡基频曲线yni需要加上第i段音阶基频函数y1i的末尾值与第i音阶过渡基频曲线yni的初始值之差, 即yni=yni+yni(t初)+y1i(t末). 移位得到的最终音阶过渡曲线的拟合函数公式为

将式(25)与式(27)联合在一起, 最终合成前4个音阶的语调基频曲线结果, 如图9所示, 其中纵坐标为频率, 横坐标为时间(t).

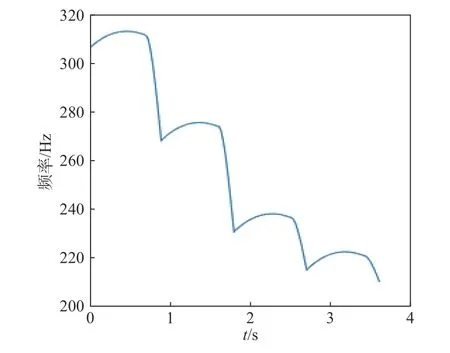
图9 4个音阶基频曲线拟合结果Fig. 9 Fitting results for fundamental curves of four scales

从曲线的合成结果看, 虽然在音阶变化阶段下降幅度较陡, 衔接处拐点明显, 但与实际情况下提取的基频取信在数值和曲线走向方面能够很好地拟合, 克服并修复了实际语音的基频曲线存在断点、不连续的情况, 拟合效果较好.

5.3 语音合成

已知任意声音信号可以由三角函数的叠加产生[7], 对应公式为

数学中, 正弦函数和余弦函数可以互相转化, 因此式(28)等效为

式(29)中,wi为第i个正弦函数的频率,t为时间,Ai为第i个正弦函数的振幅. 为实现语调控制,采用倒谱法对提取出来的基音周期f来进行函数拟合, 由于w=2πf, 因此语音信号为

采用函数叠加方法进行带音阶变化的语音合成, 其中,f1为基音频率,fi(i=2,3,···)为f1的整倍数, 即fi=f1·i(i=2,3,···), 即

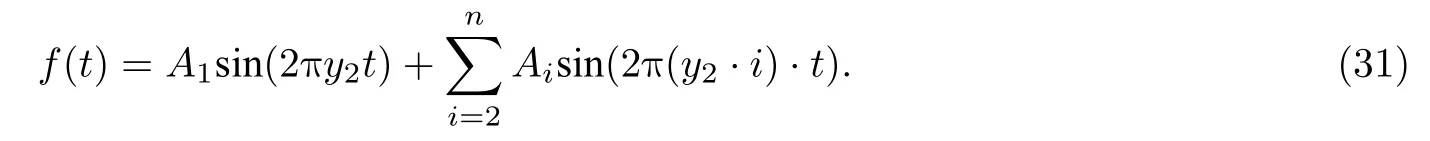
式(31)中,A1,Ai(i=2,3,···)为单个声波的声音强度(A1为基频曲线对应的声强,Ai为各谐波,即共振峰频率对应的声强),i为基音频率的整倍数(语谱图上从下至上第i条高亮线),2π(y2·i)·t为共振峰频率.

根据式(31), 以函数拟合的方式进行带有四阶降声调的语音合成, 最终由Adobe Audition软件进行语音合成分析. 图10所示为原始语音和最终合成图5中前4个音阶的语谱图对比情况(图中左侧为原始语音语谱图, 右侧为合成语音语谱图).

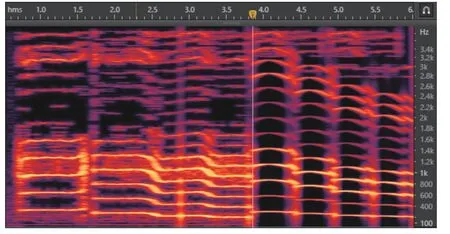
图10 原始语音与合成语音语谱图Fig. 10 Spectrum of original and synthetic speech

从处理结果可得, 实际情况下, 原始语音的音阶改变存在过渡现象, 在基频曲线上体现为两两音阶交替处存在较短时间的下降或上升, 听觉上更柔和, 但容易出现音阶变换模糊, 而实验合成结果在两两音阶的过渡衔接处基频曲线较为生硬, 听觉上音阶变化较短时间内较为直接, 但时间极短, 听觉上与原始语音差距极其微小, 可以忽略, 合成语音音阶变化清晰, 容易判断. 在图10中, 在原始语音在每一音阶范围内, 由于现实中人体收到自身及外界情况的干扰, 会出现基频走向在一定范围内的微小波动, 导致语音听觉效果稍差, 但采用函数拟合恰好可以克服人受外界因素的影响, 基频曲线清晰明了, 可以克服干扰产生的波动, 更容易控制, 在保证不失真情况下能够合成音质较好的语音.

为测试语音合成的结果, 进行主观实验对比原始语音和合成语音的自然度. 实验邀请了15位年龄在20 岁到 25岁之间, 并对音律感知较为灵敏的年轻人作为合成语音自然度测试对象. 主观测评结果见表3.

表3 测评结果Tab. 3 Evaluation results

采用支持向量机的方法对合成的语音与原始语音之间识别率进行训练并分类, 得到总体识别率为87.6%. 由于主观评价存在人体自身的影响, 而客观主要从语谱图对比出发, 因此存在一定差异. 结合主观测试和客观测试结果, 实验采用高次多项式对语音基频进行拟合, 将单一合成的基频利用分段函数进行拼接、调整以达到语音演唱的目的, 虽然部分测试者认为合成效果不理想, 但总体来看, 合成情况较好, 能够达到语音合成进一步应用的要求.

6 结 论

本文说明了语音主要具有音调、音色、响度这3要素, 基音频率、共振峰频率和幅值是语音的特征参数, 对于基频的提取, 可以根据倒谱法将声门脉冲倒谱与声道响应的倒谱相分离, 其中声门脉冲即我们所求的声带振动频率, 求共振峰频率先采用FFT对语音进行变化, 对任意频率求其功率谱, 从功率谱中分离出幅值响应, 从而得到共振峰频率及幅值大小. 从数学角度上声波可以等效为多个正弦函数的叠加, 其中, 正弦函数的幅值为分贝值(由声强变化得到), 频率为基音频率和共振峰频率, 且共振峰频率为基音频率的整倍数. 通过高次多项式函数进行声调基频曲线的拟合, 也可以构造多个分段函数实现可控的基频曲线, 最终实现不同音阶的语调变化的语音合成和演唱效果. 从声波产生的数学角度出发, 通过函数拟合得到了可以控制的基频曲线; 采用多个三角函数叠加, 实现了简单的含有音阶变换的语音演唱的合成. 相比当前较多的机器学习实现语音合成的方法而言, 实验将语调变换特征加入函数公式中, 使得语音合成的数学本质表现得更为明显, 同时弥补了当前机器合成自然度不高、缺乏情感的不足, 对今后进一步学习语音知识有一定的参考意义.